实际问题与一元一次方程01 一般行程、航行问题
文档属性
| 名称 | 实际问题与一元一次方程01 一般行程、航行问题 |

|
|
| 格式 | ppt | ||
| 文件大小 | 753.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-09-23 00:00:00 | ||
图片预览


文档简介
(共17张PPT)
义务教育课程标准实验教科书
七年级上册
路程=速度×时间
小明从家到学校,每分钟走85米,用了20分钟,小明家到学校的距离是多少?
思考:我们知道,要求小明到学校的距离,用85 ×20就能得到,你能说出所用的公式吗?
距离=速度×时间
思考:从这个公式中,你还能得到什么?
导入
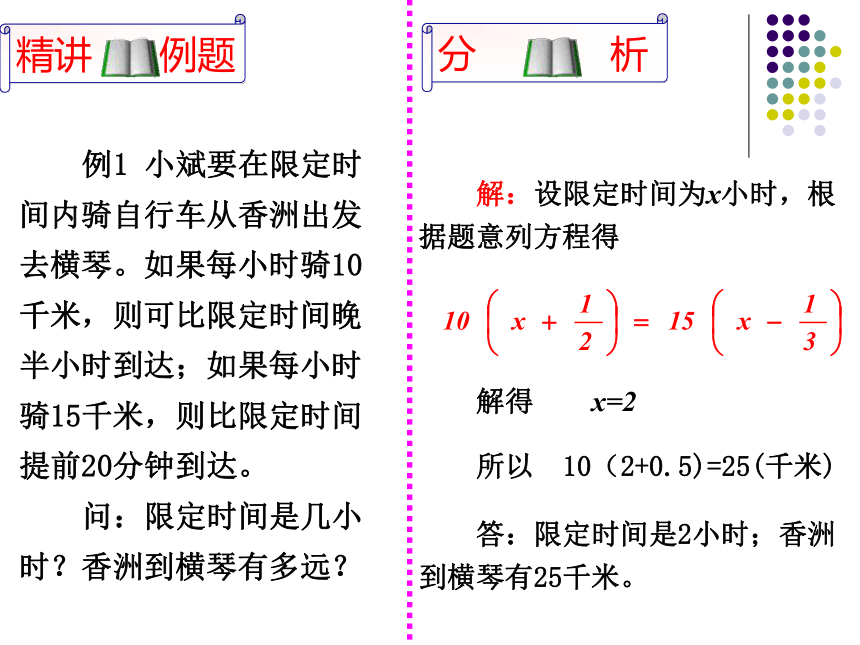
例1 小斌要在限定时间内骑自行车从香洲出发去横琴。如果每小时骑10千米,则可比限定时间晚半小时到达;如果每小时骑15千米,则比限定时间提前20分钟到达。
问:限定时间是几小时?香洲到横琴有多远?
精讲 例题
分 析
思考1:在时间、速度、路程这三个数量中,哪些是已知的?哪些是未知的?
已知:速度(每小时间骑10千米与每小时骑15千米);
未知:时间、路程。
例1 小斌要在限定时间内骑自行车从香洲出发去横琴。如果每小时骑10千米,则可比限定时间晚半小时到达;如果每小时骑15千米,则比限定时间提前20分钟到达。
问:限定时间是几小时?香洲到横琴有多远?
精讲 例题
分 析
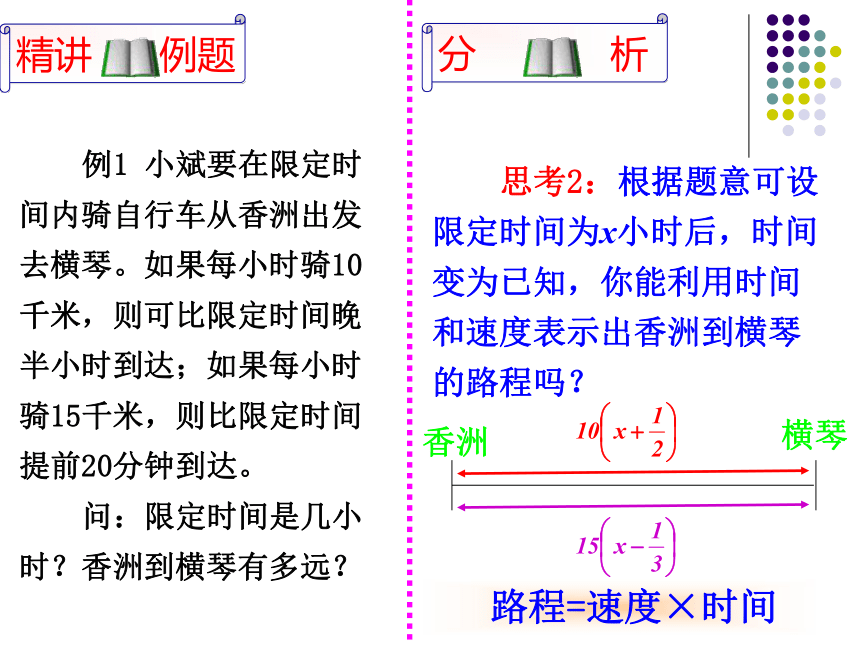
思考2:根据题意可设限定时间为x小时后,时间变为已知,你能利用时间和速度表示出香洲到横琴的路程吗?
路程=速度×时间
香洲
横琴
例1 小斌要在限定时间内骑自行车从香洲出发去横琴。如果每小时骑10千米,则可比限定时间晚半小时到达;如果每小时骑15千米,则比限定时间提前20分钟到达。
问:限定时间是几小时?香洲到横琴有多远?
精讲 例题
分 析
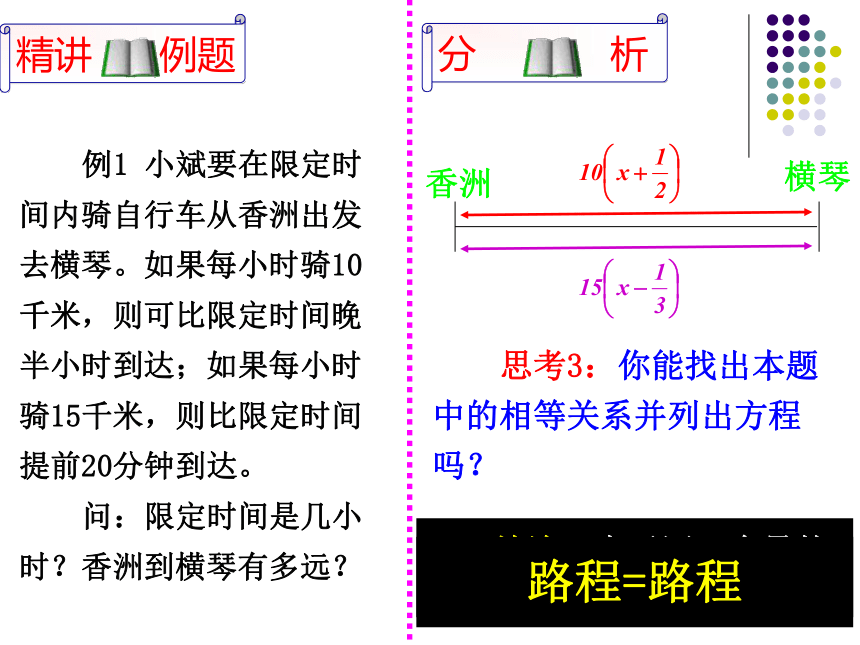
思考3:你能找出本题中的相等关系并列出方程吗?
结论:表示同一个量的两个式子具有相等关系。
香洲
横琴
路程=路程
例1 小斌要在限定时间内骑自行车从香洲出发去横琴。如果每小时骑10千米,则可比限定时间晚半小时到达;如果每小时骑15千米,则比限定时间提前20分钟到达。
问:限定时间是几小时?香洲到横琴有多远?
精讲 例题
分 析
解:设限定时间为x小时,根据题意列方程得
解得 x=2
答:限定时间是2小时;香洲到横琴有25千米。
所以 10(2+0.5)=25(千米)
例1 小斌要在限定时间内骑自行车从香洲出发去横琴。如果每小时骑10千米,则可比限定时间晚半小时到达;如果每小时骑15千米,则比限定时间提前20分钟到达。
问:限定时间是几小时?香洲到横琴有多远?
精讲 例题
分 析
思考4:本题还有没有其它设未知数的方法?根据什么相等关系列方程?
结论:表示同一个量的两个式子具有相等关系。
时间=时间
1.某部队一位驾驶员接到一个防洪的紧急任务,要在限定的时间内把一批抗洪物质从市物质局运到水库。这辆如果按每小时30千米的速度行驶,则比限定时间晚6分钟到达;他决定以每小时40千米的速度前进,结果比限定时间早到18分钟。问限定时间是几小时?市物质局仓库离水库有多远?(两种方法)
练 习
解:设限定时间为x小时,根据题意列方程得
解得 x=1.5
30x+3=40(x-0.3)
答:限定时间是1.5 小时;市物价局离水库有48千米。
所以 30×1.5+3=48(千米)
例2 (课本P12之例2)一艘船从甲码头到乙码头顺流行驶用了2小时;从乙码头返回甲码头逆流行驶用了2.5小时.已知水流的速度是3千米/时,求船在静水中的速度.
精讲 例题
分 析
一般情况下可以认为这艘船往返的路程相等。所以(填空)
顺流速度 顺流时间 逆流速度 逆流时间
结论:表示同一个量的两个式子具有相等关系。
路程=路程
例2 (课本P12之例2)一艘船从甲码头到乙码头顺流行驶用了2小时;从乙码头返回甲码头逆流行驶用了2.5小时.已知水流的速度是3千米/时,求船在静水中的速度.
精讲 例题
分 析
回顾:顺流速度、逆流速度、水速、静水速度之间有什么关系?
顺水速度=静水速度+水速
逆水速度=静水速度-水速
所以,若设船在静水中的速度为x千米/时,则顺流速度为 ,逆流速度为 。
例2 (课本P12之例2)一艘船从甲码头到乙码头顺流行驶用了2小时;从乙码头返回甲码头逆流行驶用了2.5小时.已知水流的速度是3千米/时,求船在静水中的速度.
精讲 例题
分 析
解:设船在静水中的速度为x千米/时,则顺流速度为(x+3)千米/时,逆流速度为(x-3)千米/时。根据题意列方程得
2(x+3)=2.5(x-3)
解得 x=27
答:船在静水中的速度为27千米/时。
顺流速度×顺流时间=逆流速度×逆流时间
2.一架飞机在两城之间飞行,风速为24千米/时。顺风飞行需要2小时50分,逆风飞行需要3小时,求无风时飞机的航速和两城之间的航程。
练 习
顺风速度=静风速度+风速
逆风速度=静风速度-风速
结论:表示同一个量的两个式子具有相等关系。
路程=路程
3.用绳子量井深,把绳子折成3折来量,井外余4尺;把绳折成4折来量,井外余1尺。求井深和绳长各是多少尺?
表示同一个量的两个不同式子相等
练 习
用一元一次方程分析和解决实际问题的基本过程如下:
实际问题
数学问题
(一元一次方程)
实际问题的答案
数学问题的解
(x=a)
列方程
检验
解方程
小结:这节课我们复习了一般行程问题,归纳如下:
1、在一般行程问题中,通常情况下要用到以下相等关
系:路程=速度×时间。
2、注意:
如前面所用到的:速度=速度;
时间=时间;
路程=路程。
表示同一个量的两个式子具有相等关系。
作 业
1、完成课本P79—问题(直接在书上填空);
2、作业本:
必做:课本P102—7;
“1+1”:P84—二之2;P85—二之1。
选做:课本P108—8
注:必做题必须抄题;选做题不用抄题。
义务教育课程标准实验教科书
七年级上册
路程=速度×时间
小明从家到学校,每分钟走85米,用了20分钟,小明家到学校的距离是多少?
思考:我们知道,要求小明到学校的距离,用85 ×20就能得到,你能说出所用的公式吗?
距离=速度×时间
思考:从这个公式中,你还能得到什么?
导入
例1 小斌要在限定时间内骑自行车从香洲出发去横琴。如果每小时骑10千米,则可比限定时间晚半小时到达;如果每小时骑15千米,则比限定时间提前20分钟到达。
问:限定时间是几小时?香洲到横琴有多远?
精讲 例题
分 析
思考1:在时间、速度、路程这三个数量中,哪些是已知的?哪些是未知的?
已知:速度(每小时间骑10千米与每小时骑15千米);
未知:时间、路程。
例1 小斌要在限定时间内骑自行车从香洲出发去横琴。如果每小时骑10千米,则可比限定时间晚半小时到达;如果每小时骑15千米,则比限定时间提前20分钟到达。
问:限定时间是几小时?香洲到横琴有多远?
精讲 例题
分 析
思考2:根据题意可设限定时间为x小时后,时间变为已知,你能利用时间和速度表示出香洲到横琴的路程吗?
路程=速度×时间
香洲
横琴
例1 小斌要在限定时间内骑自行车从香洲出发去横琴。如果每小时骑10千米,则可比限定时间晚半小时到达;如果每小时骑15千米,则比限定时间提前20分钟到达。
问:限定时间是几小时?香洲到横琴有多远?
精讲 例题
分 析
思考3:你能找出本题中的相等关系并列出方程吗?
结论:表示同一个量的两个式子具有相等关系。
香洲
横琴
路程=路程
例1 小斌要在限定时间内骑自行车从香洲出发去横琴。如果每小时骑10千米,则可比限定时间晚半小时到达;如果每小时骑15千米,则比限定时间提前20分钟到达。
问:限定时间是几小时?香洲到横琴有多远?
精讲 例题
分 析
解:设限定时间为x小时,根据题意列方程得
解得 x=2
答:限定时间是2小时;香洲到横琴有25千米。
所以 10(2+0.5)=25(千米)
例1 小斌要在限定时间内骑自行车从香洲出发去横琴。如果每小时骑10千米,则可比限定时间晚半小时到达;如果每小时骑15千米,则比限定时间提前20分钟到达。
问:限定时间是几小时?香洲到横琴有多远?
精讲 例题
分 析
思考4:本题还有没有其它设未知数的方法?根据什么相等关系列方程?
结论:表示同一个量的两个式子具有相等关系。
时间=时间
1.某部队一位驾驶员接到一个防洪的紧急任务,要在限定的时间内把一批抗洪物质从市物质局运到水库。这辆如果按每小时30千米的速度行驶,则比限定时间晚6分钟到达;他决定以每小时40千米的速度前进,结果比限定时间早到18分钟。问限定时间是几小时?市物质局仓库离水库有多远?(两种方法)
练 习
解:设限定时间为x小时,根据题意列方程得
解得 x=1.5
30x+3=40(x-0.3)
答:限定时间是1.5 小时;市物价局离水库有48千米。
所以 30×1.5+3=48(千米)
例2 (课本P12之例2)一艘船从甲码头到乙码头顺流行驶用了2小时;从乙码头返回甲码头逆流行驶用了2.5小时.已知水流的速度是3千米/时,求船在静水中的速度.
精讲 例题
分 析
一般情况下可以认为这艘船往返的路程相等。所以(填空)
顺流速度 顺流时间 逆流速度 逆流时间
结论:表示同一个量的两个式子具有相等关系。
路程=路程
例2 (课本P12之例2)一艘船从甲码头到乙码头顺流行驶用了2小时;从乙码头返回甲码头逆流行驶用了2.5小时.已知水流的速度是3千米/时,求船在静水中的速度.
精讲 例题
分 析
回顾:顺流速度、逆流速度、水速、静水速度之间有什么关系?
顺水速度=静水速度+水速
逆水速度=静水速度-水速
所以,若设船在静水中的速度为x千米/时,则顺流速度为 ,逆流速度为 。
例2 (课本P12之例2)一艘船从甲码头到乙码头顺流行驶用了2小时;从乙码头返回甲码头逆流行驶用了2.5小时.已知水流的速度是3千米/时,求船在静水中的速度.
精讲 例题
分 析
解:设船在静水中的速度为x千米/时,则顺流速度为(x+3)千米/时,逆流速度为(x-3)千米/时。根据题意列方程得
2(x+3)=2.5(x-3)
解得 x=27
答:船在静水中的速度为27千米/时。
顺流速度×顺流时间=逆流速度×逆流时间
2.一架飞机在两城之间飞行,风速为24千米/时。顺风飞行需要2小时50分,逆风飞行需要3小时,求无风时飞机的航速和两城之间的航程。
练 习
顺风速度=静风速度+风速
逆风速度=静风速度-风速
结论:表示同一个量的两个式子具有相等关系。
路程=路程
3.用绳子量井深,把绳子折成3折来量,井外余4尺;把绳折成4折来量,井外余1尺。求井深和绳长各是多少尺?
表示同一个量的两个不同式子相等
练 习
用一元一次方程分析和解决实际问题的基本过程如下:
实际问题
数学问题
(一元一次方程)
实际问题的答案
数学问题的解
(x=a)
列方程
检验
解方程
小结:这节课我们复习了一般行程问题,归纳如下:
1、在一般行程问题中,通常情况下要用到以下相等关
系:路程=速度×时间。
2、注意:
如前面所用到的:速度=速度;
时间=时间;
路程=路程。
表示同一个量的两个式子具有相等关系。
作 业
1、完成课本P79—问题(直接在书上填空);
2、作业本:
必做:课本P102—7;
“1+1”:P84—二之2;P85—二之1。
选做:课本P108—8
注:必做题必须抄题;选做题不用抄题。
