实际问题与一元一次方程 06 数字、比例问题
文档属性
| 名称 | 实际问题与一元一次方程 06 数字、比例问题 |

|
|
| 格式 | rar | ||
| 文件大小 | 322.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-09-23 00:00:00 | ||
图片预览



文档简介
课件10张PPT。义务教育课程标准实验教科书
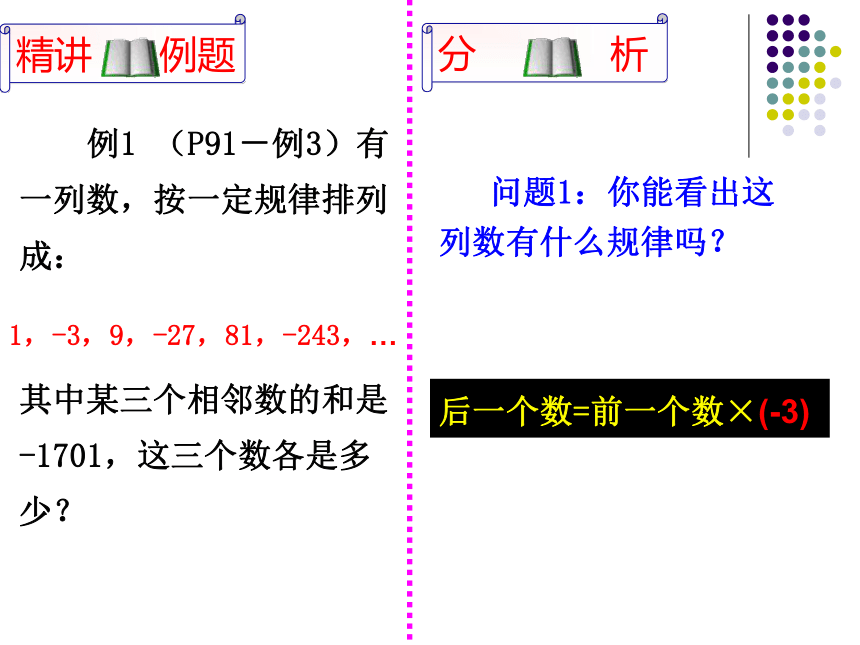
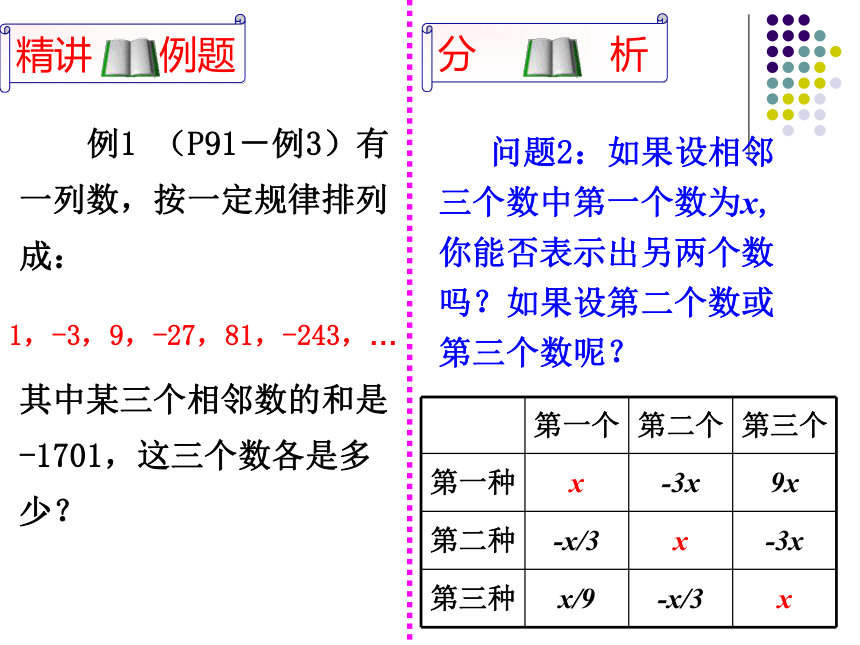
七年级上册人民教育出版社出版 王斌制作 例1 (P91-例3)有一列数,按一定规律排列成: 问题1:你能看出这列数有什么规律吗?1,-3,9,-27,81,-243,…其中某三个相邻数的和是-1701,这三个数各是多少?后一个数=前一个数×(-3) 例1 (P91-例3)有一列数,按一定规律排列成:1,-3,9,-27,81,-243,…其中某三个相邻数的和是-1701,这三个数各是多少? 问题2:如果设相邻三个数中第一个数为x,你能否表示出另两个数吗?如果设第二个数或第三个数呢? 1. 三个连续奇数的和93,求这三个数。
2. 有一个两位数,它的两个数字之和是8,把这个两位数的数字交换位置后所得的数乘以原来的数就得到1855,求原来的两位数。 思考:
(1)在三位数345中,3,4,5是这个三位数的什么?
(2)如果a ,b ,c 分别表示百位数字、十位数字、个位数字,这个三位数能不能写成abc形式?为什么? 例2 甲、乙、丙三数之比是2:3:7,三数之和是48,求这三个数? 问题1:此题用算术方法非常容易求解。你能用列方程的方法解决吗?如何设未知数? 如果设甲数为x,则乙数为 ,丙数为 ,由相等关系“甲数+乙数+丙数=48可列方程 。 例2 甲、乙、丙三数之比是2:3:7,三数之和是48,求这三个数? 问题2:有没有更简单的设未知数的方法? 事实上,我们可以将三数之和看作分为(2+3+7=)12份,并设一份为x,则甲数为 ,乙数为 ,丙数为 ,由相等关系“甲数+乙数+丙数=48可列方程 。 3、 一个三角形三条边长之比为2:4:5,最长的边比最短的边长6cm。这个三角形的三条边长分别是多少厘米?最长的边—最短的边=6 4、 甲、乙、丙三位同学向贫困地区的少年儿童捐献图书,已知这三位同学捐赠图书册数的比为5:6:9。
(1)如果他们共捐书320册,那么这三位同学各捐书多少册?
(2)如果甲、丙两位同学捐书的册数的和是乙捐书册数的2倍还多12册,那么他们各捐书多少册?(1)相等关系
甲册数+乙册数+丙册数=320(2)相等关系
甲册数+乙册数=丙册数×2+12用一元一次方程分析和解决实际问题的基本过程如下:实际问题数学问题
(一元一次方程)实际问题的答案数学问题的解
(x=a)列方程检验解方程小结:这节课我们学习了数字、比例问题,归纳如下: 你又什么收获?
七年级上册人民教育出版社出版 王斌制作 例1 (P91-例3)有一列数,按一定规律排列成: 问题1:你能看出这列数有什么规律吗?1,-3,9,-27,81,-243,…其中某三个相邻数的和是-1701,这三个数各是多少?后一个数=前一个数×(-3) 例1 (P91-例3)有一列数,按一定规律排列成:1,-3,9,-27,81,-243,…其中某三个相邻数的和是-1701,这三个数各是多少? 问题2:如果设相邻三个数中第一个数为x,你能否表示出另两个数吗?如果设第二个数或第三个数呢? 1. 三个连续奇数的和93,求这三个数。
2. 有一个两位数,它的两个数字之和是8,把这个两位数的数字交换位置后所得的数乘以原来的数就得到1855,求原来的两位数。 思考:
(1)在三位数345中,3,4,5是这个三位数的什么?
(2)如果a ,b ,c 分别表示百位数字、十位数字、个位数字,这个三位数能不能写成abc形式?为什么? 例2 甲、乙、丙三数之比是2:3:7,三数之和是48,求这三个数? 问题1:此题用算术方法非常容易求解。你能用列方程的方法解决吗?如何设未知数? 如果设甲数为x,则乙数为 ,丙数为 ,由相等关系“甲数+乙数+丙数=48可列方程 。 例2 甲、乙、丙三数之比是2:3:7,三数之和是48,求这三个数? 问题2:有没有更简单的设未知数的方法? 事实上,我们可以将三数之和看作分为(2+3+7=)12份,并设一份为x,则甲数为 ,乙数为 ,丙数为 ,由相等关系“甲数+乙数+丙数=48可列方程 。 3、 一个三角形三条边长之比为2:4:5,最长的边比最短的边长6cm。这个三角形的三条边长分别是多少厘米?最长的边—最短的边=6 4、 甲、乙、丙三位同学向贫困地区的少年儿童捐献图书,已知这三位同学捐赠图书册数的比为5:6:9。
(1)如果他们共捐书320册,那么这三位同学各捐书多少册?
(2)如果甲、丙两位同学捐书的册数的和是乙捐书册数的2倍还多12册,那么他们各捐书多少册?(1)相等关系
甲册数+乙册数+丙册数=320(2)相等关系
甲册数+乙册数=丙册数×2+12用一元一次方程分析和解决实际问题的基本过程如下:实际问题数学问题
(一元一次方程)实际问题的答案数学问题的解
(x=a)列方程检验解方程小结:这节课我们学习了数字、比例问题,归纳如下: 你又什么收获?
