2.2 圆的对称性 2023-2024学年苏科版九年级上册暑假衔接课讲义(无答案)
文档属性
| 名称 | 2.2 圆的对称性 2023-2024学年苏科版九年级上册暑假衔接课讲义(无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 486.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-24 00:00:00 | ||
图片预览


文档简介
§2.2 圆的对称性
相关知识点回顾
1、圆:如图,把线段OP绕着端点O在平面内旋转 周,端点P运动所形成的图形叫做 。
2、轴对称图形:把一个图形沿着 折叠,如果直线两旁的部分能够 ,那么称这个图形是轴对称图形,这条直线就是 。
3、中心对称图形:把一个平面图形绕某一点旋转 ,如果旋转后的图形能够和原来的图形 ,那么这个图形叫做中心对称图形,这个点就是它的 。
知识点1:圆的对称性
通过旋转与折叠的方法,我们得到:
★ 圆的旋转不变性,即一个圆绕圆心旋转任何角度后,都与它自身重合;
★ 圆是 图形,圆心是它的对称中心;
★ 圆是 图形,过圆心的任意一条直线都是它的对称轴,对称抽有无数条。
【典型例题1】世界上因为有了圆的图案,万物才显得富有生机,以下来自现实生活的图中都有圆:它们看上去多么美丽与和谐,这正是因为圆具有轴对称和中心对称性。
(1)请问图中三个图形中是轴对称图形的有 ,是中心对称图形的有 (分别用三个图的代号a、b、c填空).
(2)请你在图d、e两个圆中,按要求分别画出与a、b、c图案不重复的图案(草图)(用尺规画或徒手画均可,但要尽可能准确些,美观些).
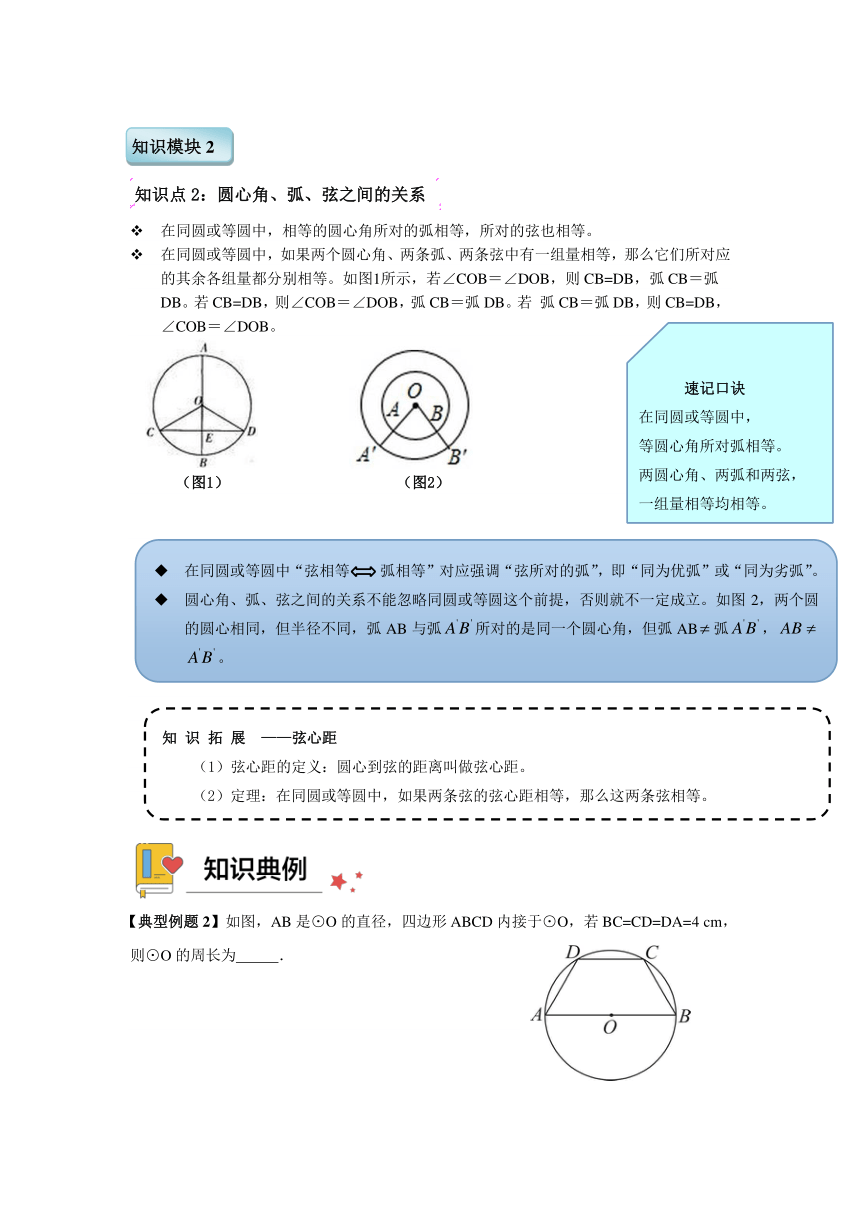
知识点2:圆心角、弧、弦之间的关系
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等。
在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等。如图1所示,若∠COB=∠DOB,则CB=DB,弧CB=弧DB。若CB=DB,则∠COB=∠DOB,弧CB=弧DB。若 弧CB=弧DB,则CB=DB,∠COB=∠DOB。
(图1) (图2)
【典型例题2】如图,AB是⊙O的直径,四边形ABCD内接于⊙O,若BC=CD=DA=4 cm,则⊙O的周长为 .
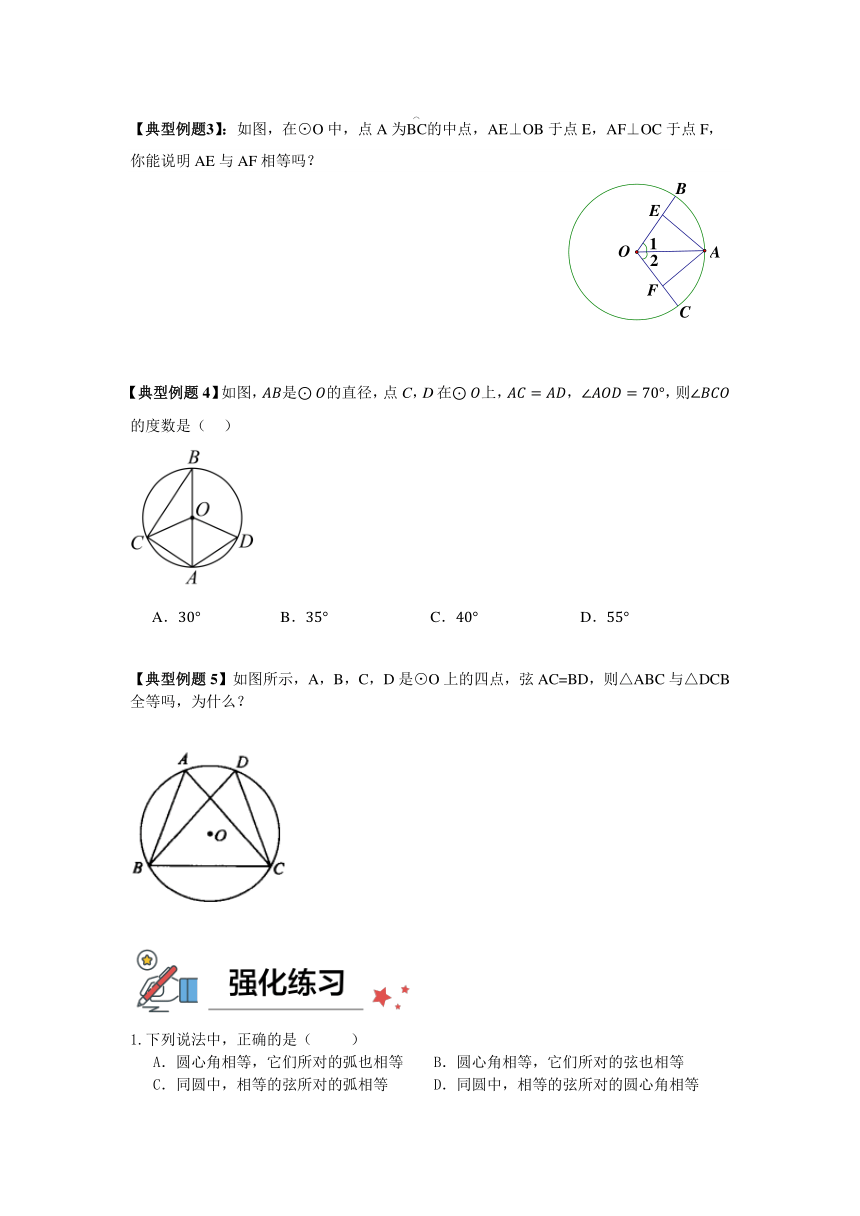
【典型例题3】:如图,在⊙O中,点A为BC (⌒)的中点,AE⊥OB于点E,AF⊥OC于点F,你能说明AE与AF相等吗?
【典型例题4】如图,是的直径,点C,D在上,,则的度数是( )
A. B. C. D.
【典型例题5】如图所示,A,B,C,D是⊙O上的四点,弦AC=BD,则△ABC与△DCB全等吗,为什么?
1.下列说法中,正确的是( )
A.圆心角相等,它们所对的弧也相等 B.圆心角相等,它们所对的弦也相等
C.同圆中,相等的弦所对的弧相等 D.同圆中,相等的弦所对的圆心角相等
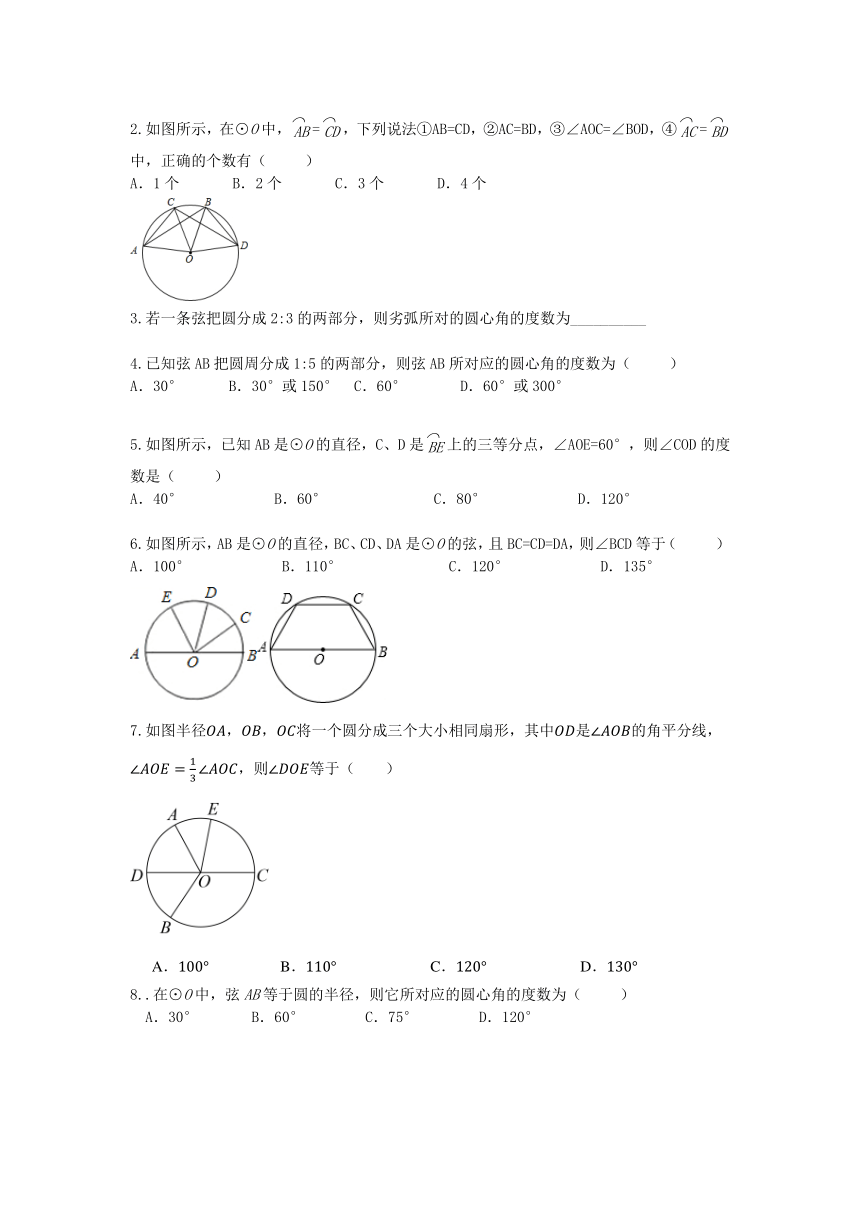
2.如图所示,在⊙O中,=,下列说法①AB=CD,②AC=BD,③∠AOC=∠BOD,④=中,正确的个数有( )
A.1个 B.2个 C.3个 D.4个
3.若一条弦把圆分成2:3的两部分,则劣弧所对的圆心角的度数为__________
4.已知弦AB把圆周分成1:5的两部分,则弦AB所对应的圆心角的度数为( )
A.30° B.30°或150° C.60° D.60°或300°
5.如图所示,已知AB是⊙O的直径,C、D是上的三等分点,∠AOE=60°,则∠COD的度数是( )
A.40° B.60° C.80° D.120°
6.如图所示,AB是⊙O的直径,BC、CD、DA是⊙O的弦,且BC=CD=DA,则∠BCD等于( )
A.100° B.110° C.120° D.135°
7.如图半径将一个圆分成三个大小相同扇形,其中是的角平分线,,则等于( )
A. B. C. D.
8..在⊙O中,弦AB等于圆的半径,则它所对应的圆心角的度数为( )
A.30° B.60° C.75° D.120°
在⊙O中,AD=BC,试说明AB与CD相等。
知识点3:圆心角的度数与它所对的弧的度数的关系
★ 1的弧:将顶点在圆心的周角等分360份,每一份圆心角是1的角,因为同圆中相等的圆心角所对的弧相等,所以整个圆也被等分成360份,我们把1的圆心角所对的弧叫做1的弧。
★ 圆心角的度数与它所对的弧的度数的关系:一般地,n的圆心角对着n的弧,n的弧对着n的圆心角,即圆心角的度数与它所对的弧的度数相等。
【典型例题5】 如图,是半圆,O为AB中点,C、D两点在上,且AD∥OC,连接BC、BD.若=62°,则的度数为何?( )
A.56 B.58 C.60 D.62
【典型例题6】如图,在△ABC中,∠ACB=90,∠B=25,以点C为圆心,CA为半径的圆交AB于点D,求AD (⌒)的度数。
1.如图,在⊙O中,∠B=37°,则劣弧的度数为( )
A.106° B.126° C.75° D.53°
2. 如图,AB和CD是⊙O的两条直径,弦DE∥AB,弧DE为50°的弧,那么∠BOC为( )
A.115° B.100° C.80° D.50°
3.如图,在⊙O中,弦AC∥半径OB,∠BOC=50°,则∠OAB的度数为()
A.25° B.50° C.60° D.30°
4.如图,在中,,以点C为圆心,为半径的圆交于点D,交于点E,求的度数.
6.把一张圆形纸片按如图所示方式折叠两次后展开,图中的虚线表示折痕,则的度数是( )
A.120° B.135° C.150° D.165°
7.如图所示,将圆沿AB折叠后,圆弧恰好经过圆心,则弧AB等于( )
A.60° B. 90° C.120° D.150°
8.如图,已知为半圆的直径.求作矩形,使得点,在上,点,在半圆上,且.要求:(1)用直尺和圆规作图;(2)保留作图的痕迹,写出必要的文字说明.
知识点4:垂径定理
★ 垂径定理:____________________________________________________________;
★ 垂径定理的符号语言表现形式: ;
★ 拓展:圆的两条平行弦所夹的弧相等。
【典型例题7】 如图所示,弦CD垂直于⊙O的直径AB,垂足为点H,且CD=,BD=,则AB的长为( )
A.2 B.3 C.4 D.5
【典型例题8】如图,⊙O的半径为4cm,弦AB垂直平分半径OC,求弦AB的长。
1.如图1所示,AB是⊙O的弦,半径于点D,且,,则DC的长为( )。
A.5cm B.2.5cm C.2cm D. 1cm
(图1) (图2)
如图2所示,AB为⊙O的直径,弦CD⊥AB,垂足为点E,连接OC,若OC=5,CD=8,则AE
3.如图所示,以点P为圆心的圆弧与轴交于A,B两点,点P的坐标为(4,2),点A的坐标为(2,0),则点B的坐标为_________________。
4.如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,AB=20,CD=16,则线段OE的长为( )
A.4 B.6 C.8 D.10
5.如图,是的中点,,若,,则所在圆的半径为_____ 。
6.如图,⊙O的直径AB=12,CD是⊙O的弦,CD⊥AB,垂足为P,且BP:AP=1:5,则CD长为( )
A. B. C. D.
7.如图,在Rt△ABC中,,以点C为圆心,CA长为半径的圆与AB交于点D,则AD的长为( )
8.如图,在中,已知,,,以点为圆心,为半径的圆交于点,则的长为_____ 。
10.已知的直径,是的弦,,且,垂足为,则的长为( )。
A: B: C: 或 D: 或
11.如图所示,在圆O内有折线OABC,其中OA=8,AB=12,∠A=∠B=60°,求BC的长。
12.如图所示,AB,CD是半径长为5的⊙O的两条弦,AB=8,CD=6,MN是直径,AB⊥MN于点E,CD⊥MN于点F,P为EF上的任意一点,则PA+PC的最小值为_____________。
13.如图,在平面直角坐标系中,一个圆与两坐标轴分别交于A、B、C、D四点.已知A(6,0),B(﹣2,0),C(0,3),则点D的坐标为 .
14..如图,在⊙O中,AB是直径,P为AB上一点,过点P作弦MN,∠NPB=45°.
(1)若AP=2,BP=6,求MN的长;
(2)若MP=3,NP=5,求AB的长;
16.如图,是某隧道的入口,它的截面如图所示,是由和直角围成,且点也在所在的圆上,已知,隧道的最高点离路面的距离,则该道路的路面宽 m;在上,离地面相同高度的两点,装有两排照明灯,若是的中点,则这两排照明灯离地面的高度是 m.
相关知识点回顾
1、圆:如图,把线段OP绕着端点O在平面内旋转 周,端点P运动所形成的图形叫做 。
2、轴对称图形:把一个图形沿着 折叠,如果直线两旁的部分能够 ,那么称这个图形是轴对称图形,这条直线就是 。
3、中心对称图形:把一个平面图形绕某一点旋转 ,如果旋转后的图形能够和原来的图形 ,那么这个图形叫做中心对称图形,这个点就是它的 。
知识点1:圆的对称性
通过旋转与折叠的方法,我们得到:
★ 圆的旋转不变性,即一个圆绕圆心旋转任何角度后,都与它自身重合;
★ 圆是 图形,圆心是它的对称中心;
★ 圆是 图形,过圆心的任意一条直线都是它的对称轴,对称抽有无数条。
【典型例题1】世界上因为有了圆的图案,万物才显得富有生机,以下来自现实生活的图中都有圆:它们看上去多么美丽与和谐,这正是因为圆具有轴对称和中心对称性。
(1)请问图中三个图形中是轴对称图形的有 ,是中心对称图形的有 (分别用三个图的代号a、b、c填空).
(2)请你在图d、e两个圆中,按要求分别画出与a、b、c图案不重复的图案(草图)(用尺规画或徒手画均可,但要尽可能准确些,美观些).
知识点2:圆心角、弧、弦之间的关系
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等。
在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等。如图1所示,若∠COB=∠DOB,则CB=DB,弧CB=弧DB。若CB=DB,则∠COB=∠DOB,弧CB=弧DB。若 弧CB=弧DB,则CB=DB,∠COB=∠DOB。
(图1) (图2)
【典型例题2】如图,AB是⊙O的直径,四边形ABCD内接于⊙O,若BC=CD=DA=4 cm,则⊙O的周长为 .
【典型例题3】:如图,在⊙O中,点A为BC (⌒)的中点,AE⊥OB于点E,AF⊥OC于点F,你能说明AE与AF相等吗?
【典型例题4】如图,是的直径,点C,D在上,,则的度数是( )
A. B. C. D.
【典型例题5】如图所示,A,B,C,D是⊙O上的四点,弦AC=BD,则△ABC与△DCB全等吗,为什么?
1.下列说法中,正确的是( )
A.圆心角相等,它们所对的弧也相等 B.圆心角相等,它们所对的弦也相等
C.同圆中,相等的弦所对的弧相等 D.同圆中,相等的弦所对的圆心角相等
2.如图所示,在⊙O中,=,下列说法①AB=CD,②AC=BD,③∠AOC=∠BOD,④=中,正确的个数有( )
A.1个 B.2个 C.3个 D.4个
3.若一条弦把圆分成2:3的两部分,则劣弧所对的圆心角的度数为__________
4.已知弦AB把圆周分成1:5的两部分,则弦AB所对应的圆心角的度数为( )
A.30° B.30°或150° C.60° D.60°或300°
5.如图所示,已知AB是⊙O的直径,C、D是上的三等分点,∠AOE=60°,则∠COD的度数是( )
A.40° B.60° C.80° D.120°
6.如图所示,AB是⊙O的直径,BC、CD、DA是⊙O的弦,且BC=CD=DA,则∠BCD等于( )
A.100° B.110° C.120° D.135°
7.如图半径将一个圆分成三个大小相同扇形,其中是的角平分线,,则等于( )
A. B. C. D.
8..在⊙O中,弦AB等于圆的半径,则它所对应的圆心角的度数为( )
A.30° B.60° C.75° D.120°
在⊙O中,AD=BC,试说明AB与CD相等。
知识点3:圆心角的度数与它所对的弧的度数的关系
★ 1的弧:将顶点在圆心的周角等分360份,每一份圆心角是1的角,因为同圆中相等的圆心角所对的弧相等,所以整个圆也被等分成360份,我们把1的圆心角所对的弧叫做1的弧。
★ 圆心角的度数与它所对的弧的度数的关系:一般地,n的圆心角对着n的弧,n的弧对着n的圆心角,即圆心角的度数与它所对的弧的度数相等。
【典型例题5】 如图,是半圆,O为AB中点,C、D两点在上,且AD∥OC,连接BC、BD.若=62°,则的度数为何?( )
A.56 B.58 C.60 D.62
【典型例题6】如图,在△ABC中,∠ACB=90,∠B=25,以点C为圆心,CA为半径的圆交AB于点D,求AD (⌒)的度数。
1.如图,在⊙O中,∠B=37°,则劣弧的度数为( )
A.106° B.126° C.75° D.53°
2. 如图,AB和CD是⊙O的两条直径,弦DE∥AB,弧DE为50°的弧,那么∠BOC为( )
A.115° B.100° C.80° D.50°
3.如图,在⊙O中,弦AC∥半径OB,∠BOC=50°,则∠OAB的度数为()
A.25° B.50° C.60° D.30°
4.如图,在中,,以点C为圆心,为半径的圆交于点D,交于点E,求的度数.
6.把一张圆形纸片按如图所示方式折叠两次后展开,图中的虚线表示折痕,则的度数是( )
A.120° B.135° C.150° D.165°
7.如图所示,将圆沿AB折叠后,圆弧恰好经过圆心,则弧AB等于( )
A.60° B. 90° C.120° D.150°
8.如图,已知为半圆的直径.求作矩形,使得点,在上,点,在半圆上,且.要求:(1)用直尺和圆规作图;(2)保留作图的痕迹,写出必要的文字说明.
知识点4:垂径定理
★ 垂径定理:____________________________________________________________;
★ 垂径定理的符号语言表现形式: ;
★ 拓展:圆的两条平行弦所夹的弧相等。
【典型例题7】 如图所示,弦CD垂直于⊙O的直径AB,垂足为点H,且CD=,BD=,则AB的长为( )
A.2 B.3 C.4 D.5
【典型例题8】如图,⊙O的半径为4cm,弦AB垂直平分半径OC,求弦AB的长。
1.如图1所示,AB是⊙O的弦,半径于点D,且,,则DC的长为( )。
A.5cm B.2.5cm C.2cm D. 1cm
(图1) (图2)
如图2所示,AB为⊙O的直径,弦CD⊥AB,垂足为点E,连接OC,若OC=5,CD=8,则AE
3.如图所示,以点P为圆心的圆弧与轴交于A,B两点,点P的坐标为(4,2),点A的坐标为(2,0),则点B的坐标为_________________。
4.如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,AB=20,CD=16,则线段OE的长为( )
A.4 B.6 C.8 D.10
5.如图,是的中点,,若,,则所在圆的半径为_____ 。
6.如图,⊙O的直径AB=12,CD是⊙O的弦,CD⊥AB,垂足为P,且BP:AP=1:5,则CD长为( )
A. B. C. D.
7.如图,在Rt△ABC中,,以点C为圆心,CA长为半径的圆与AB交于点D,则AD的长为( )
8.如图,在中,已知,,,以点为圆心,为半径的圆交于点,则的长为_____ 。
10.已知的直径,是的弦,,且,垂足为,则的长为( )。
A: B: C: 或 D: 或
11.如图所示,在圆O内有折线OABC,其中OA=8,AB=12,∠A=∠B=60°,求BC的长。
12.如图所示,AB,CD是半径长为5的⊙O的两条弦,AB=8,CD=6,MN是直径,AB⊥MN于点E,CD⊥MN于点F,P为EF上的任意一点,则PA+PC的最小值为_____________。
13.如图,在平面直角坐标系中,一个圆与两坐标轴分别交于A、B、C、D四点.已知A(6,0),B(﹣2,0),C(0,3),则点D的坐标为 .
14..如图,在⊙O中,AB是直径,P为AB上一点,过点P作弦MN,∠NPB=45°.
(1)若AP=2,BP=6,求MN的长;
(2)若MP=3,NP=5,求AB的长;
16.如图,是某隧道的入口,它的截面如图所示,是由和直角围成,且点也在所在的圆上,已知,隧道的最高点离路面的距离,则该道路的路面宽 m;在上,离地面相同高度的两点,装有两排照明灯,若是的中点,则这两排照明灯离地面的高度是 m.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
