2.6 正多边形与圆 课后练习(对点练习+拓展练习+2024中考直击)(无答案)2024-2025学年 苏科版数学九年级上册
文档属性
| 名称 | 2.6 正多边形与圆 课后练习(对点练习+拓展练习+2024中考直击)(无答案)2024-2025学年 苏科版数学九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-24 18:54:17 | ||
图片预览




文档简介
§2.6 正多边形与圆 课后练习
(对点练习+拓展练习+2024中考直击)
题型1:正多边形的概念及与圆的结合
题型2:正多边形的性质
题型3:正多边形综合拓展
题型4:2024中考真题直击
(1)若一个正多边形的边长与半径相等,则这个正多边形的中心角是( )
A.45° B.60° C.90° D.120° (2)已知正n边形的内角和是它的外角和的3倍,则这个正n边形的中心角为( )
B. C. D.
(3)如图,点,,,,,分别是正六边形各边的中点,则六边形与六边形的周长比为 .
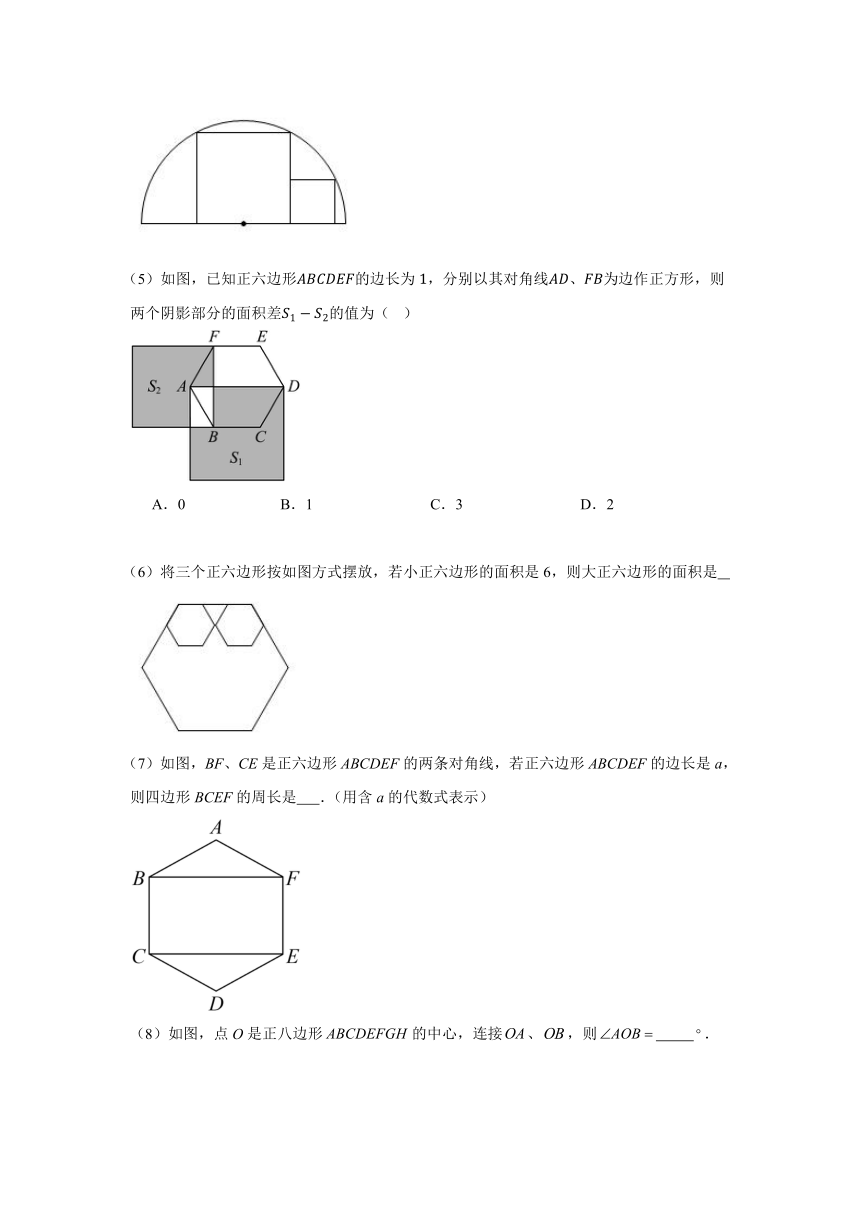
(4)如图,两正方形彼此相邻且内接于半圆,若小正方形的面积为,则该半圆的半径为 .
(5)如图,已知正六边形的边长为,分别以其对角线、为边作正方形,则两个阴影部分的面积差的值为( )
A.0 B.1 C.3 D.2
(6)将三个正六边形按如图方式摆放,若小正六边形的面积是6,则大正六边形的面积是
(7)如图,BF、CE是正六边形ABCDEF的两条对角线,若正六边形ABCDEF的边长是a,则四边形BCEF的周长是 .(用含a的代数式表示)
(8)如图,点O是正八边形的中心,连接、,则 .
(9)如图,正六边形的中心为原点O,顶点在x轴上,半径为.求其各个顶点的坐标.
(10)我们学习了,多边形中,如果各条边都相等,各个内角都相等,这样的多边形叫做正多边形观察每个正多边形中的变化情况,解答下列问题:
(1)将如表的表格补充完整:
正多边形边数 ______
的 度数 ______ ______ ______ ______
(2)根据规律,是否存在一个正边形,使其中的?若存在,直接写出的值;若不存在,请说明理由.
(1)同一个圆的内接正方形和正三角形的边心距的比为 .
(2)如图,正方形内接于,点E在上连接,若,则( )
B. C. D.
(3)如图,点是正六边形的中心,则的度数是( )
B. C. D.
(4)如图,正六边形内接于,P为上的一点(点P不与点A,B重合),则的度数为 .
(5)如图,正五边形内接于,点F是上的动点,则∠AFC的度数为 .
(6)如图,正方形内接于,连接,点F是的中点,过点D作的切线与的延长线相交于点G.
(7)如图,正六边形内接于,半径,求边心距的长.
(8)如图,正六边形和正方形都内接于,连接,则弦所对圆周角的度数为( )
A. B. C.或 D.或
(9)如图,正五边形内接于,是的直径,P是上的一点(不与点B,F重合),则的度数为 °.
(10))已如:⊙O与⊙O上的一点A
(1)求作:⊙O的内接正六边形ABCDEF;( 要求:尺规作图,不写作法但保留作图痕迹)
(2)连接CE,BF,判断四边形BCEF是否为矩形,并说明理由.
(1)如图所示,在正五边形中,是的中点,点在线段上运动,连接,当的周长最小时,的度数为 .
(2)如图,在的内接正六边形中,,则图中阴影部分的面积为 .
(3)已知四个正六边形按如图所示摆放在图中,顶点A,B,C,D,E,F均在上,连接.若两个大正六边形的边长均为4,两个小正六边形全等,则小正六边形的边长是( )
(4)如图,在圆内接正六边形中,,交于点G,已知半径为,则的长为 .
(5)如图所示,已知边长为2的正三角形ABC顶点A的坐标为(0,6),BC的中点D在y轴上,且在点A下方,点E是边长为2,中心在原点的正六边形的一个顶点,把这个正六边形绕中心旋转一周,在此过程中DE的最小值为( )
A. B. C. D.
(6)将三个相同的六角形螺母并排摆放在桌面上,从上面看到的图形如图1所示,正六边形边长为,且各有一个顶点在直线上,两侧螺母不动,把中间螺母抽出并重新摆放后,从上面看到的图形如图2所示,其中,中间正六边形的一边与直线平行,有两边分别经过两侧正六边形的一个顶点,正六边形边直线.则 .
(1)(2023·河北·中考真题)如图,点是的八等分点.若,四边形的周长分别为a,b,则下列正确的是( )
A. B. C. D.a,b大小无法比较
(2)(2024·四川甘孜·中考真题)如图,正六边形内接于,,则的长为( )
A.2 B. C.1 D.
(4)(2024·河北·中考真题)直线l与正六边形的边分别相交于点M,N,如图所示,则( )
B. C. D.
(5)(2024·山东威海·中考真题)如图,在正六边形中,,,垂足为点I.若,则 .
(6)(2024·江苏连云港·中考真题)【问题情境】
如图1,圆与大正方形的各边都相切,小正方形是圆的内接正方形,那么大正方形面积是小正方形面积的几倍?小昕将小正方形绕圆心旋转45°(如图2),这时候就容易发现大正方形面积是小正方形面积的__________倍.由此可见,图形变化是解决问题的有效策略;
(7)(2024·甘肃临夏·中考真题)“香渡栏干屈曲,红妆映、薄绮疏棂.”图1窗棂的外边框为正六边形(如图2),则该正六边形的每个内角为 .
(对点练习+拓展练习+2024中考直击)
题型1:正多边形的概念及与圆的结合
题型2:正多边形的性质
题型3:正多边形综合拓展
题型4:2024中考真题直击
(1)若一个正多边形的边长与半径相等,则这个正多边形的中心角是( )
A.45° B.60° C.90° D.120° (2)已知正n边形的内角和是它的外角和的3倍,则这个正n边形的中心角为( )
B. C. D.
(3)如图,点,,,,,分别是正六边形各边的中点,则六边形与六边形的周长比为 .
(4)如图,两正方形彼此相邻且内接于半圆,若小正方形的面积为,则该半圆的半径为 .
(5)如图,已知正六边形的边长为,分别以其对角线、为边作正方形,则两个阴影部分的面积差的值为( )
A.0 B.1 C.3 D.2
(6)将三个正六边形按如图方式摆放,若小正六边形的面积是6,则大正六边形的面积是
(7)如图,BF、CE是正六边形ABCDEF的两条对角线,若正六边形ABCDEF的边长是a,则四边形BCEF的周长是 .(用含a的代数式表示)
(8)如图,点O是正八边形的中心,连接、,则 .
(9)如图,正六边形的中心为原点O,顶点在x轴上,半径为.求其各个顶点的坐标.
(10)我们学习了,多边形中,如果各条边都相等,各个内角都相等,这样的多边形叫做正多边形观察每个正多边形中的变化情况,解答下列问题:
(1)将如表的表格补充完整:
正多边形边数 ______
的 度数 ______ ______ ______ ______
(2)根据规律,是否存在一个正边形,使其中的?若存在,直接写出的值;若不存在,请说明理由.
(1)同一个圆的内接正方形和正三角形的边心距的比为 .
(2)如图,正方形内接于,点E在上连接,若,则( )
B. C. D.
(3)如图,点是正六边形的中心,则的度数是( )
B. C. D.
(4)如图,正六边形内接于,P为上的一点(点P不与点A,B重合),则的度数为 .
(5)如图,正五边形内接于,点F是上的动点,则∠AFC的度数为 .
(6)如图,正方形内接于,连接,点F是的中点,过点D作的切线与的延长线相交于点G.
(7)如图,正六边形内接于,半径,求边心距的长.
(8)如图,正六边形和正方形都内接于,连接,则弦所对圆周角的度数为( )
A. B. C.或 D.或
(9)如图,正五边形内接于,是的直径,P是上的一点(不与点B,F重合),则的度数为 °.
(10))已如:⊙O与⊙O上的一点A
(1)求作:⊙O的内接正六边形ABCDEF;( 要求:尺规作图,不写作法但保留作图痕迹)
(2)连接CE,BF,判断四边形BCEF是否为矩形,并说明理由.
(1)如图所示,在正五边形中,是的中点,点在线段上运动,连接,当的周长最小时,的度数为 .
(2)如图,在的内接正六边形中,,则图中阴影部分的面积为 .
(3)已知四个正六边形按如图所示摆放在图中,顶点A,B,C,D,E,F均在上,连接.若两个大正六边形的边长均为4,两个小正六边形全等,则小正六边形的边长是( )
(4)如图,在圆内接正六边形中,,交于点G,已知半径为,则的长为 .
(5)如图所示,已知边长为2的正三角形ABC顶点A的坐标为(0,6),BC的中点D在y轴上,且在点A下方,点E是边长为2,中心在原点的正六边形的一个顶点,把这个正六边形绕中心旋转一周,在此过程中DE的最小值为( )
A. B. C. D.
(6)将三个相同的六角形螺母并排摆放在桌面上,从上面看到的图形如图1所示,正六边形边长为,且各有一个顶点在直线上,两侧螺母不动,把中间螺母抽出并重新摆放后,从上面看到的图形如图2所示,其中,中间正六边形的一边与直线平行,有两边分别经过两侧正六边形的一个顶点,正六边形边直线.则 .
(1)(2023·河北·中考真题)如图,点是的八等分点.若,四边形的周长分别为a,b,则下列正确的是( )
A. B. C. D.a,b大小无法比较
(2)(2024·四川甘孜·中考真题)如图,正六边形内接于,,则的长为( )
A.2 B. C.1 D.
(4)(2024·河北·中考真题)直线l与正六边形的边分别相交于点M,N,如图所示,则( )
B. C. D.
(5)(2024·山东威海·中考真题)如图,在正六边形中,,,垂足为点I.若,则 .
(6)(2024·江苏连云港·中考真题)【问题情境】
如图1,圆与大正方形的各边都相切,小正方形是圆的内接正方形,那么大正方形面积是小正方形面积的几倍?小昕将小正方形绕圆心旋转45°(如图2),这时候就容易发现大正方形面积是小正方形面积的__________倍.由此可见,图形变化是解决问题的有效策略;
(7)(2024·甘肃临夏·中考真题)“香渡栏干屈曲,红妆映、薄绮疏棂.”图1窗棂的外边框为正六边形(如图2),则该正六边形的每个内角为 .
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
