2.7 弧长及扇形的面积 课后练习(对点练习+拓展练习+2024中考直击)(无答案)2024-2025学年苏科版数学九年级上册
文档属性
| 名称 | 2.7 弧长及扇形的面积 课后练习(对点练习+拓展练习+2024中考直击)(无答案)2024-2025学年苏科版数学九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-24 19:13:51 | ||
图片预览



文档简介
§2.7 弧长及扇形的面积 课后练习
(对点练习+拓展练习+2024中考直击)
题型1:扇形的弧长
题型2:扇形的面积
题型3:扇形弧长和面积综合拓展
题型4:2024中考真题直击
(1)半径为5cm的圆内接正五边形一边所对劣弧的长为 cm.
(2)如图,在扇形中,,,则的长为 .
(3)如图,在Rt△ABC中,∠C=90°,∠B=30°,AB=8,以点C为圆心,CA的长为半径画弧,交AB于点D,交BC于点E,则弧DE的长为( )
A. B. C. D.
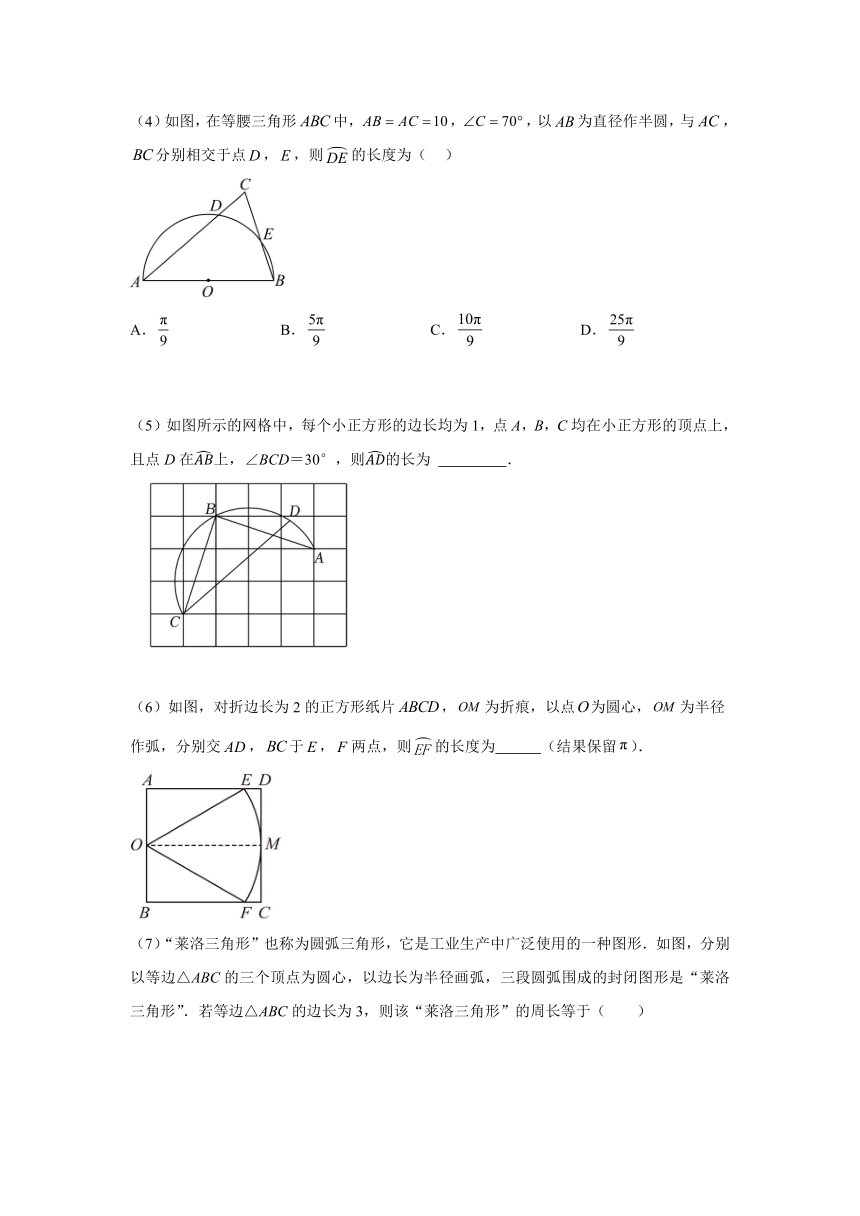
(4)如图,在等腰三角形中,,,以为直径作半圆,与,分别相交于点,,则的长度为( )
A. B. C. D.
(5)如图所示的网格中,每个小正方形的边长均为1,点A,B,C均在小正方形的顶点上,且点D在上,∠BCD=30°,则的长为 .
(6)如图,对折边长为2的正方形纸片,为折痕,以点为圆心,为半径作弧,分别交,于,两点,则的长度为 (结果保留).
(7)“莱洛三角形”也称为圆弧三角形,它是工业生产中广泛使用的一种图形.如图,分别以等边△ABC的三个顶点为圆心,以边长为半径画弧,三段圆弧围成的封闭图形是“莱洛三角形”.若等边△ABC的边长为3,则该“莱洛三角形”的周长等于( )
A.π B.3π C.2π D.2π
(8)如图1是一段弯管,弯管的部分外轮廓线如图2所示是一条圆弧,圆弧的半径OA=20cm,圆心角∠AOB=90°,则( )
A.20πcm B.10πcm C.5πcm D.2πcm
(9)为了促进城乡协调发展,实现共同富裕,某乡镇计划修建公路.如图、与是公路弯道的外、内边线,它们有共同的圆心O,所对的圆心角都是,点A,C,O在同一条直线上,公路弯道外侧边线比内侧边线多36米,则公路宽的长是 米.(取3.14,计算结果精确到0.1)
(10)铁艺花窗是园林设计中常见的装饰元素.如图是一个花瓣造型的花窗示意图,由六条等弧连接而成,六条弧所对应的弦构成一个正六边形,中心为点O,所在圆的圆心C恰好是的内心,若,则花窗的周长(图中实线部分的长度) .(结果保留)
(1)如图,正六边形ABCDEF的外接圆⊙O的半径为2,过圆心O的两条直线l1、l2的夹角为60°,则图中的阴影部分的面积为( )
A.π B.π C.π D.π
(2))如图,在矩形中,,O为中点,,则扇形的面积为 .
(3)如图,边长为的正方形ABCD内接于⊙O,分别过点A,D作⊙O的切线,两条切线交于点P,则图中阴影部分的面积是 .
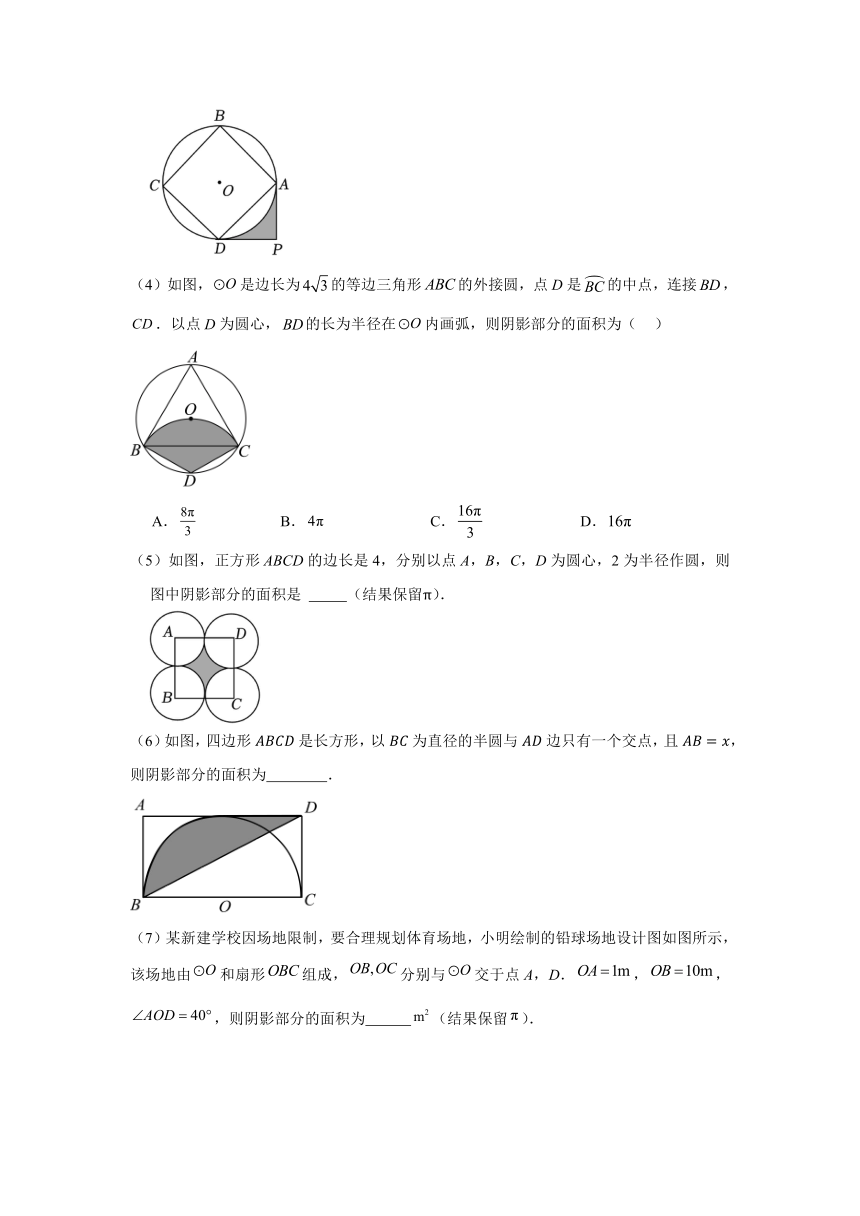
(4)如图,是边长为的等边三角形的外接圆,点D是的中点,连接,.以点D为圆心,的长为半径在内画弧,则阴影部分的面积为( )
A. B. C. D.
(5)如图,正方形ABCD的边长是4,分别以点A,B,C,D为圆心,2为半径作圆,则图中阴影部分的面积是 (结果保留π).
(6)如图,四边形是长方形,以为直径的半圆与边只有一个交点,且,则阴影部分的面积为 .
(7)某新建学校因场地限制,要合理规划体育场地,小明绘制的铅球场地设计图如图所示,该场地由和扇形组成,分别与交于点A,D.,,,则阴影部分的面积为 (结果保留).
(10)如图,点E是正方形ABCD的边BC延长线上一点,且AC=CE,连接AE交CD于点O,以点O为圆心,OD为半径作⊙O,⊙O交线段AO于点F.
(1)求证:AC是⊙O的切线;
(2)若,求阴影部分的面积.
(1)一块含角的直角三角板按如图所示的方式摆放,边与直线重合,.现将该三角板绕点顺时针旋转,使点的对应点落在直线上,则点A经过的路径长至少为 .(结果保留)
(2)如图1,点是半圆上一个动点,点从点开始向终点运动的整个过程中,的弧长与时间(秒)的函数关系如图2所示,则点运动至秒时,的度数为( )
A. B. C. D.
(3)如图,量角器的直径与直角三角板ABC的斜边重合(),其中量角器0刻度线的端点N与点A重合,射线从处出发沿顺时针方向以每秒3度的速度旋转,与量角器的半圆弧交于点E,第20秒时点E在量角器上运动路径长是 .
(4)如图,已知的半径为1,内接于,,则弓形ACB(阴影部分)的面积为 .(结果保留或根号)
(5)如图,在中,直径,点D为上方圆上的一点,,于点E,点P是上一点,连接,得出下列结论:
Ⅰ:阴影部分的面积随着点P的位置的改变而改变,其最小值为.
Ⅱ:阴影部分的周长随着点P的位置的改变而改变,其最小值为.
下列判断正确的是( ).
A.只有Ⅰ正确 B.只有Ⅱ正确 C.Ⅰ、Ⅱ都正确 D.Ⅰ、Ⅱ都不正确
(6)在平面内,将小棒经过适当的运动,使它调转方向(调转前后的小棒不一定在同一条直线上),那么小棒扫过区域的面积如何尽可能地小呢?
已知小棒长度为4,宽度不计.
方案1:将小棒绕中点O旋转180°到,设小棒扫过区域的面积为(即图中灰色区域的面积,下同);
方案2:将小棒先绕A逆时针旋转60°到,再绕C逆时针旋转60°到,最后绕B逆时针旋转60°到,设小棒扫过区域的面积为.
(1)①______,______;(结果保留)
②比较与的大小.(参考数据:,.)
(2)方案2可优化为方案3:首次旋转后,将小棒先沿着小棒所在的直线平移再分别进行第2、3次旋转,三次旋转扫过的面积会重叠更多,最终小棒扫过的区域是一个等边三角形.
①补全方案3的示意图;
②设方案3中小棒扫过区域的面积为,求.
(3)设计方案4,使小棒扫过区域的面积小于,画出示意图并说明理由.
(1)(2024·安徽·中考真题)若扇形的半径为6,,则的长为( )
A. B. C. D.
(2)(2024·贵州·中考真题)如图,在扇形纸扇中,若,,则的长为( )
B. C. D.
(3)(2024·四川遂宁·中考真题)工人师傅在检查排污管道时发现淤泥堆积.如图所示,排污管道的横截面是直径为米的圆,为预估淤泥量,测得淤泥横截面(图中阴影部分)宽为米,请计算出淤泥横截面的面积( )
A. B. C. D.
(4)(2024·四川自贡·中考真题)龚扇是自贡“小三绝”之一.为弘扬民族传统文化,某校手工兴趣小组将一个废弃的大纸杯侧面剪开直接当作扇面,制作了一个龚扇模型(如图).扇形外侧两竹条夹角为.长,扇面的边长为,则扇面面积为 (结果保留).
(5)(2024·山东·中考真题)如图,在四边形中,,,.以点为圆心,以为半径作交于点,以点为圆心,以为半径作所交于点,连接交于另一点,连接.
(1)求证:为所在圆的切线;
(2)求图中阴影部分面积.(结果保留)
(6)(2024·青海·中考真题)如图,直线经过点C,且,.
(1)求证:直线是的切线;
(2)若圆的半径为4,,求阴影部分的面积.
(对点练习+拓展练习+2024中考直击)
题型1:扇形的弧长
题型2:扇形的面积
题型3:扇形弧长和面积综合拓展
题型4:2024中考真题直击
(1)半径为5cm的圆内接正五边形一边所对劣弧的长为 cm.
(2)如图,在扇形中,,,则的长为 .
(3)如图,在Rt△ABC中,∠C=90°,∠B=30°,AB=8,以点C为圆心,CA的长为半径画弧,交AB于点D,交BC于点E,则弧DE的长为( )
A. B. C. D.
(4)如图,在等腰三角形中,,,以为直径作半圆,与,分别相交于点,,则的长度为( )
A. B. C. D.
(5)如图所示的网格中,每个小正方形的边长均为1,点A,B,C均在小正方形的顶点上,且点D在上,∠BCD=30°,则的长为 .
(6)如图,对折边长为2的正方形纸片,为折痕,以点为圆心,为半径作弧,分别交,于,两点,则的长度为 (结果保留).
(7)“莱洛三角形”也称为圆弧三角形,它是工业生产中广泛使用的一种图形.如图,分别以等边△ABC的三个顶点为圆心,以边长为半径画弧,三段圆弧围成的封闭图形是“莱洛三角形”.若等边△ABC的边长为3,则该“莱洛三角形”的周长等于( )
A.π B.3π C.2π D.2π
(8)如图1是一段弯管,弯管的部分外轮廓线如图2所示是一条圆弧,圆弧的半径OA=20cm,圆心角∠AOB=90°,则( )
A.20πcm B.10πcm C.5πcm D.2πcm
(9)为了促进城乡协调发展,实现共同富裕,某乡镇计划修建公路.如图、与是公路弯道的外、内边线,它们有共同的圆心O,所对的圆心角都是,点A,C,O在同一条直线上,公路弯道外侧边线比内侧边线多36米,则公路宽的长是 米.(取3.14,计算结果精确到0.1)
(10)铁艺花窗是园林设计中常见的装饰元素.如图是一个花瓣造型的花窗示意图,由六条等弧连接而成,六条弧所对应的弦构成一个正六边形,中心为点O,所在圆的圆心C恰好是的内心,若,则花窗的周长(图中实线部分的长度) .(结果保留)
(1)如图,正六边形ABCDEF的外接圆⊙O的半径为2,过圆心O的两条直线l1、l2的夹角为60°,则图中的阴影部分的面积为( )
A.π B.π C.π D.π
(2))如图,在矩形中,,O为中点,,则扇形的面积为 .
(3)如图,边长为的正方形ABCD内接于⊙O,分别过点A,D作⊙O的切线,两条切线交于点P,则图中阴影部分的面积是 .
(4)如图,是边长为的等边三角形的外接圆,点D是的中点,连接,.以点D为圆心,的长为半径在内画弧,则阴影部分的面积为( )
A. B. C. D.
(5)如图,正方形ABCD的边长是4,分别以点A,B,C,D为圆心,2为半径作圆,则图中阴影部分的面积是 (结果保留π).
(6)如图,四边形是长方形,以为直径的半圆与边只有一个交点,且,则阴影部分的面积为 .
(7)某新建学校因场地限制,要合理规划体育场地,小明绘制的铅球场地设计图如图所示,该场地由和扇形组成,分别与交于点A,D.,,,则阴影部分的面积为 (结果保留).
(10)如图,点E是正方形ABCD的边BC延长线上一点,且AC=CE,连接AE交CD于点O,以点O为圆心,OD为半径作⊙O,⊙O交线段AO于点F.
(1)求证:AC是⊙O的切线;
(2)若,求阴影部分的面积.
(1)一块含角的直角三角板按如图所示的方式摆放,边与直线重合,.现将该三角板绕点顺时针旋转,使点的对应点落在直线上,则点A经过的路径长至少为 .(结果保留)
(2)如图1,点是半圆上一个动点,点从点开始向终点运动的整个过程中,的弧长与时间(秒)的函数关系如图2所示,则点运动至秒时,的度数为( )
A. B. C. D.
(3)如图,量角器的直径与直角三角板ABC的斜边重合(),其中量角器0刻度线的端点N与点A重合,射线从处出发沿顺时针方向以每秒3度的速度旋转,与量角器的半圆弧交于点E,第20秒时点E在量角器上运动路径长是 .
(4)如图,已知的半径为1,内接于,,则弓形ACB(阴影部分)的面积为 .(结果保留或根号)
(5)如图,在中,直径,点D为上方圆上的一点,,于点E,点P是上一点,连接,得出下列结论:
Ⅰ:阴影部分的面积随着点P的位置的改变而改变,其最小值为.
Ⅱ:阴影部分的周长随着点P的位置的改变而改变,其最小值为.
下列判断正确的是( ).
A.只有Ⅰ正确 B.只有Ⅱ正确 C.Ⅰ、Ⅱ都正确 D.Ⅰ、Ⅱ都不正确
(6)在平面内,将小棒经过适当的运动,使它调转方向(调转前后的小棒不一定在同一条直线上),那么小棒扫过区域的面积如何尽可能地小呢?
已知小棒长度为4,宽度不计.
方案1:将小棒绕中点O旋转180°到,设小棒扫过区域的面积为(即图中灰色区域的面积,下同);
方案2:将小棒先绕A逆时针旋转60°到,再绕C逆时针旋转60°到,最后绕B逆时针旋转60°到,设小棒扫过区域的面积为.
(1)①______,______;(结果保留)
②比较与的大小.(参考数据:,.)
(2)方案2可优化为方案3:首次旋转后,将小棒先沿着小棒所在的直线平移再分别进行第2、3次旋转,三次旋转扫过的面积会重叠更多,最终小棒扫过的区域是一个等边三角形.
①补全方案3的示意图;
②设方案3中小棒扫过区域的面积为,求.
(3)设计方案4,使小棒扫过区域的面积小于,画出示意图并说明理由.
(1)(2024·安徽·中考真题)若扇形的半径为6,,则的长为( )
A. B. C. D.
(2)(2024·贵州·中考真题)如图,在扇形纸扇中,若,,则的长为( )
B. C. D.
(3)(2024·四川遂宁·中考真题)工人师傅在检查排污管道时发现淤泥堆积.如图所示,排污管道的横截面是直径为米的圆,为预估淤泥量,测得淤泥横截面(图中阴影部分)宽为米,请计算出淤泥横截面的面积( )
A. B. C. D.
(4)(2024·四川自贡·中考真题)龚扇是自贡“小三绝”之一.为弘扬民族传统文化,某校手工兴趣小组将一个废弃的大纸杯侧面剪开直接当作扇面,制作了一个龚扇模型(如图).扇形外侧两竹条夹角为.长,扇面的边长为,则扇面面积为 (结果保留).
(5)(2024·山东·中考真题)如图,在四边形中,,,.以点为圆心,以为半径作交于点,以点为圆心,以为半径作所交于点,连接交于另一点,连接.
(1)求证:为所在圆的切线;
(2)求图中阴影部分面积.(结果保留)
(6)(2024·青海·中考真题)如图,直线经过点C,且,.
(1)求证:直线是的切线;
(2)若圆的半径为4,,求阴影部分的面积.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
