22.2二次函数与一元二次方程课件(共16张PPT) 2024-2025学年人教版九年级数学上册
文档属性
| 名称 | 22.2二次函数与一元二次方程课件(共16张PPT) 2024-2025学年人教版九年级数学上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-24 00:00:00 | ||
图片预览





文档简介
(共16张PPT)
22.2 二次函数与一元二次方程
复习回顾
向上
x=-2
(-2,-1)
-2
小
-1
(-1,0),(-3,0)
(0,3)
-1
-3
从上面的问题中,你能发现二次函数y=x2+4x+3与一元二次方程x2+4x+3=0有什么联系吗?
探究活动
思考:
从上面的问题中,你能发现二次函数y=ax2+bx+c(a≠0)与一元二次方程ax2+bx+c=0(a≠0)有什么联系吗?
探究活动
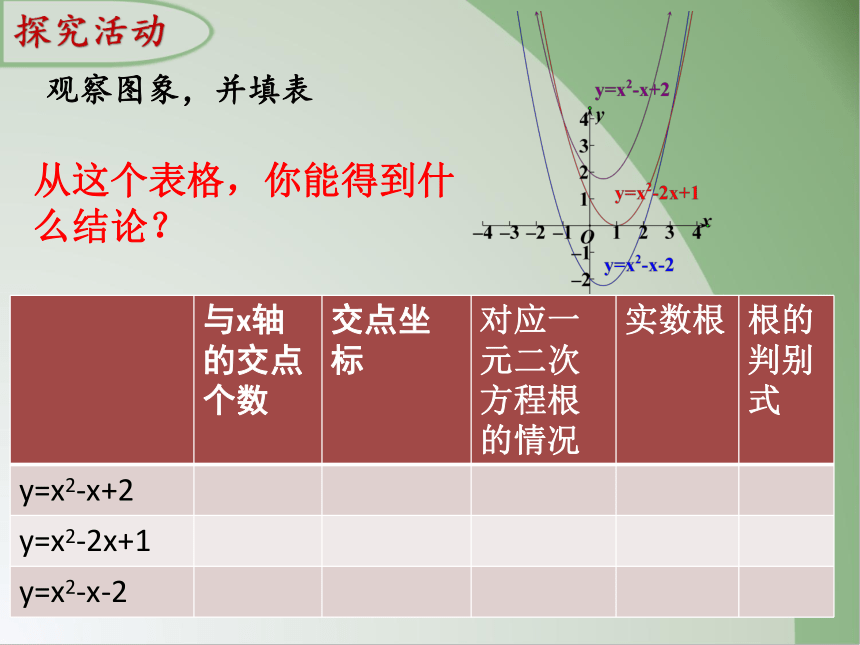
观察图象,并填表
与x轴的交点个数 交点坐标 对应一元二次方程根的情况 实数根 根的判别式
y=x2-x+2
y=x2-2x+1
y=x2-x-2
从这个表格,你能得到什么结论?
归纳规律
1、抛物线与x轴的交点个数与一元二次方程根的情况、根的判别式之间的关系
抛物线与x轴的交点个数 一元二次方程根的情况 根的判别式
2个
1个
0个
归纳规律
2、二次函数y=ax2+bx+c(a≠0)与一元二次方程ax2+bx+c=0(a≠0)的联系
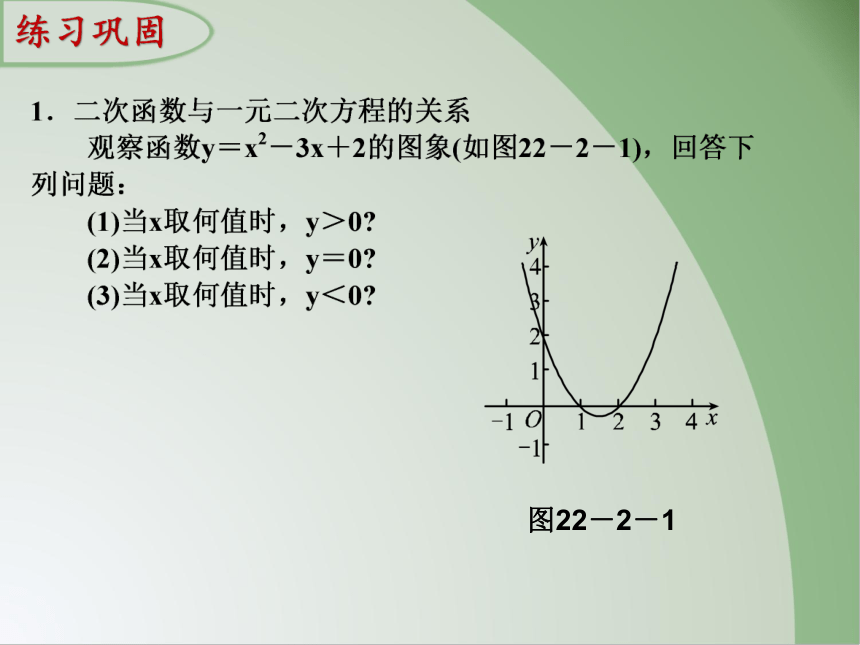
练习巩固
图22-2-1
图22-2-2
练习巩固
拓展延伸
你能利用函数y=-x2+2x-3的图象,求方程
-x2+2x-3=-8的近似解吗?
思考:
拓展延伸
拓展延伸
总结步骤
如图22-2-4所示,你能直观地看出哪些方程的根?
练习巩固
图22-2-4
课堂总结
(1)本节课学了哪些主要内容?
(2)通过你对函数和方程之间的联系有什么新的体会?……
(3)数学思想……
通过这节课的学习,谈谈你掌握了什么?
布置作业
必做题:1、课本47页 习题22.2 第 3、5、6 题.
选做题:阅读课本48页,探索二次函数的性质
再见!
22.2 二次函数与一元二次方程
复习回顾
向上
x=-2
(-2,-1)
-2
小
-1
(-1,0),(-3,0)
(0,3)
-1
-3
从上面的问题中,你能发现二次函数y=x2+4x+3与一元二次方程x2+4x+3=0有什么联系吗?
探究活动
思考:
从上面的问题中,你能发现二次函数y=ax2+bx+c(a≠0)与一元二次方程ax2+bx+c=0(a≠0)有什么联系吗?
探究活动
观察图象,并填表
与x轴的交点个数 交点坐标 对应一元二次方程根的情况 实数根 根的判别式
y=x2-x+2
y=x2-2x+1
y=x2-x-2
从这个表格,你能得到什么结论?
归纳规律
1、抛物线与x轴的交点个数与一元二次方程根的情况、根的判别式之间的关系
抛物线与x轴的交点个数 一元二次方程根的情况 根的判别式
2个
1个
0个
归纳规律
2、二次函数y=ax2+bx+c(a≠0)与一元二次方程ax2+bx+c=0(a≠0)的联系
练习巩固
图22-2-1
图22-2-2
练习巩固
拓展延伸
你能利用函数y=-x2+2x-3的图象,求方程
-x2+2x-3=-8的近似解吗?
思考:
拓展延伸
拓展延伸
总结步骤
如图22-2-4所示,你能直观地看出哪些方程的根?
练习巩固
图22-2-4
课堂总结
(1)本节课学了哪些主要内容?
(2)通过你对函数和方程之间的联系有什么新的体会?……
(3)数学思想……
通过这节课的学习,谈谈你掌握了什么?
布置作业
必做题:1、课本47页 习题22.2 第 3、5、6 题.
选做题:阅读课本48页,探索二次函数的性质
再见!
同课章节目录
