20.1.1 平均数 课件 (共20张PPT) 2023-2024学年人教版八年级数学下册
文档属性
| 名称 | 20.1.1 平均数 课件 (共20张PPT) 2023-2024学年人教版八年级数学下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-24 19:20:30 | ||
图片预览






文档简介
(共20张PPT)
20.1 数据的集中趋势
20.1.1 平均数
人教版八年级下册
7
6
5
4
3
2
1
A B C D
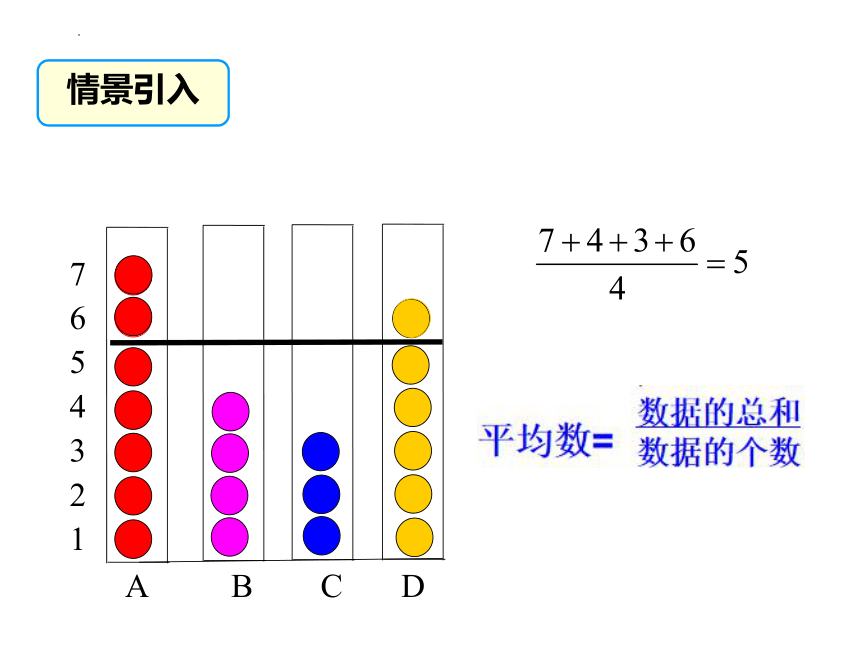
情景引入
如果将 5 种口味各取1斤混合出售,那么混合巧克力的平均单价是多少元呢?
口味 麦芽脆心 香浓黑巧 榛仁果粒 奶香白巧 牛奶丝滑
单价(元/斤) 48 50 55 40 52
研究实例,探索新知
n
(巧克力价格分别为 x1元/斤,x2元/斤,…,xn元/斤)
一般地,对于 n 个数 x1,x2,…,xn,我们把 ( x1+x2+…+xn )
叫做这 n 个数的算术平均数,简称平均数。 记为 x 。
算术平均数
1
n
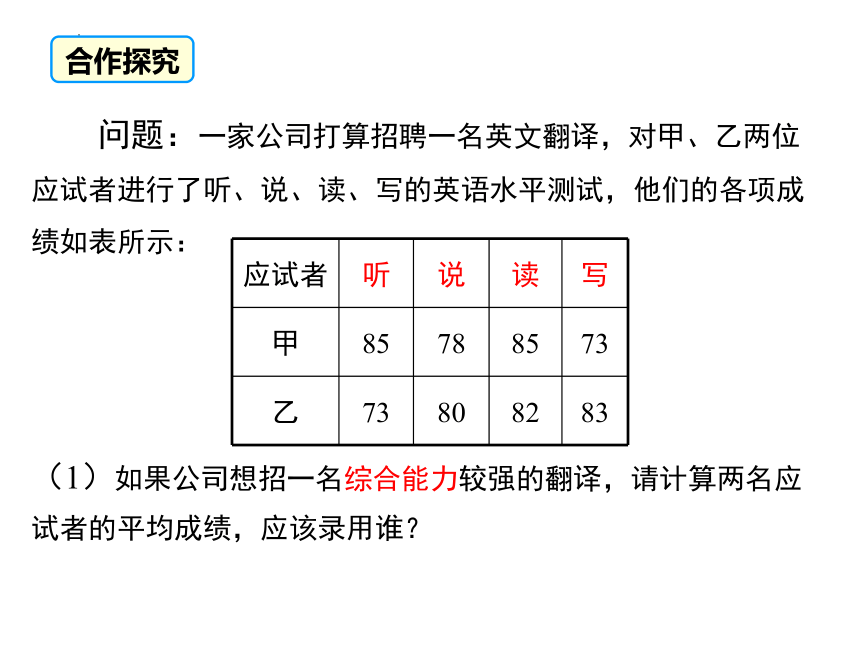
问题:一家公司打算招聘一名英文翻译,对甲、乙两位应试者进行了听、说、读、写的英语水平测试,他们的各项成绩如表所示:
(1)如果公司想招一名综合能力较强的翻译,请计算两名应 试者的平均成绩,应该录用谁?
应试者 听 说 读 写
甲 85 78 85 73
乙 73 80 82 83
合作探究
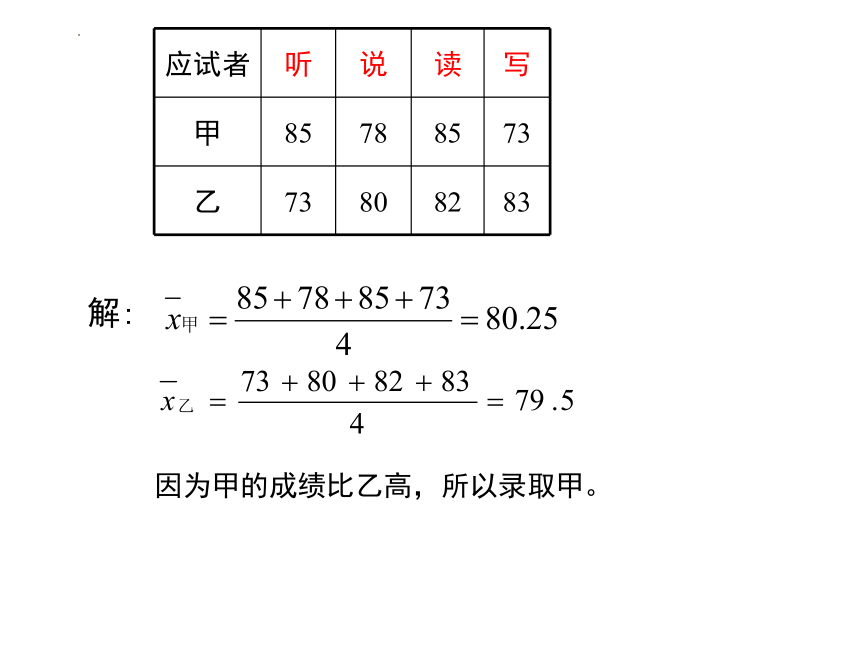
因为甲的成绩比乙高,所以录取甲。
解:
应试者 听 说 读 写
甲 85 78 85 73
乙 73 80 82 83
(2)公司想招一名笔译能力较强的翻译
应试者 听 说 读 写
甲 85 78 85 73
乙 73 80 82 83
1、能否同等看待听、说、读、写的成绩?
2、听、说、读、写的成绩按 2:1:3:4 的比确定,
说明在计算平均数中比较侧重哪些成绩?
2 : 1 : 3 : 4
因为乙的成绩比甲高,所以录取乙。
解:
应试者 听2份 说1份 读3份 写4份
甲 85 78 85 73
乙 73 80 82 83
权的英文是weight,有表示数据重要程度的意思。
权
一般地,若n个数x1, x2, …, xn的权分别是w1,w2,…,wn ,则
叫做这n个数的加权平均数。
=
归
纳
概
念
(3)如果公司想招一名口语能力较强的翻译,听、说、读、写的成绩按照3:3:2:2的比确定,那么甲、乙两人谁将被录取?
解:
因为甲的成绩比乙高,所以应该录取甲。
应试者 听 说 读 写
甲 85 78 85 73
乙 73 80 82 83
与上述问题中的(1)(2)相比较,你能体会到权的作用吗?
思考:算术平均数和加权平均数有区别和联系吗?
算术平均数是加权平均数的一种特殊情况(它特殊在各项的权相等)
权反映数据的重要程度,权的改变会影响这组数据的平均水平。
一次演讲比赛中,评委将以下三个方面为选手打分,各项成绩均按百分制,计算选手的综合成绩(百分制)。进入决赛的前两名选手的单项成绩如下表所示,请确定两人的名次。
选手 演讲内容 演讲能力 演讲效果
A 85 95 95
B 95 85 95
典例精析
解:
由上可知选手B获得第一名,选手A获得第二名。
选手 演讲内容 演讲能力 演讲效果
A 85 95 95
B 95 85 95
解:
思考:例题中两名选手的单项成绩都是两个95分与
一个85分,为什么他们的最后得分不同呢?
权反映数据的重要程度,权的改变会影响这组数据的平均水平。
所以,当一组数据中各个数据的权不同,即重要程度不同时,选择加权平均数能更好地反映这组数据的平均水平。
总
结
归
纳
权的表现形式:
比例、百分比
你能体会到权的作用吗?
幸运3+1
分宜县某校拟招聘一名优秀数学老师,现有甲乙两名教师入围,学校将录取得分最高者,如果面试和笔试成绩的权分别为6和4,从他们的成绩看,你认为应该录取谁?
应试者 面试 笔试
甲 86 90
乙 92 83
幸
运
3
+
1
加2分
已知一组数据4,12,24的权数分别是50%,20%,30%,则这组数据的加权平均数是________ .
11.6
幸
运
3
+
1
加3分
恭喜你,直接通关!加1分
幸
运
3
+
1
一组数据为10,8, ,12,13,这组数据的平均数是10,则 的值为_________。
7
加2分
注:每项满分10分
课
堂
小
结
请同学们根据自己的表现,并依据表格提供信息,设计评分方案,看看谁的表现最棒!
知识掌握 解决问题 课堂表现
得分
权
成绩 课本第113页练习1、2
课
后
作
业
20.1 数据的集中趋势
20.1.1 平均数
人教版八年级下册
7
6
5
4
3
2
1
A B C D
情景引入
如果将 5 种口味各取1斤混合出售,那么混合巧克力的平均单价是多少元呢?
口味 麦芽脆心 香浓黑巧 榛仁果粒 奶香白巧 牛奶丝滑
单价(元/斤) 48 50 55 40 52
研究实例,探索新知
n
(巧克力价格分别为 x1元/斤,x2元/斤,…,xn元/斤)
一般地,对于 n 个数 x1,x2,…,xn,我们把 ( x1+x2+…+xn )
叫做这 n 个数的算术平均数,简称平均数。 记为 x 。
算术平均数
1
n
问题:一家公司打算招聘一名英文翻译,对甲、乙两位应试者进行了听、说、读、写的英语水平测试,他们的各项成绩如表所示:
(1)如果公司想招一名综合能力较强的翻译,请计算两名应 试者的平均成绩,应该录用谁?
应试者 听 说 读 写
甲 85 78 85 73
乙 73 80 82 83
合作探究
因为甲的成绩比乙高,所以录取甲。
解:
应试者 听 说 读 写
甲 85 78 85 73
乙 73 80 82 83
(2)公司想招一名笔译能力较强的翻译
应试者 听 说 读 写
甲 85 78 85 73
乙 73 80 82 83
1、能否同等看待听、说、读、写的成绩?
2、听、说、读、写的成绩按 2:1:3:4 的比确定,
说明在计算平均数中比较侧重哪些成绩?
2 : 1 : 3 : 4
因为乙的成绩比甲高,所以录取乙。
解:
应试者 听2份 说1份 读3份 写4份
甲 85 78 85 73
乙 73 80 82 83
权的英文是weight,有表示数据重要程度的意思。
权
一般地,若n个数x1, x2, …, xn的权分别是w1,w2,…,wn ,则
叫做这n个数的加权平均数。
=
归
纳
概
念
(3)如果公司想招一名口语能力较强的翻译,听、说、读、写的成绩按照3:3:2:2的比确定,那么甲、乙两人谁将被录取?
解:
因为甲的成绩比乙高,所以应该录取甲。
应试者 听 说 读 写
甲 85 78 85 73
乙 73 80 82 83
与上述问题中的(1)(2)相比较,你能体会到权的作用吗?
思考:算术平均数和加权平均数有区别和联系吗?
算术平均数是加权平均数的一种特殊情况(它特殊在各项的权相等)
权反映数据的重要程度,权的改变会影响这组数据的平均水平。
一次演讲比赛中,评委将以下三个方面为选手打分,各项成绩均按百分制,计算选手的综合成绩(百分制)。进入决赛的前两名选手的单项成绩如下表所示,请确定两人的名次。
选手 演讲内容 演讲能力 演讲效果
A 85 95 95
B 95 85 95
典例精析
解:
由上可知选手B获得第一名,选手A获得第二名。
选手 演讲内容 演讲能力 演讲效果
A 85 95 95
B 95 85 95
解:
思考:例题中两名选手的单项成绩都是两个95分与
一个85分,为什么他们的最后得分不同呢?
权反映数据的重要程度,权的改变会影响这组数据的平均水平。
所以,当一组数据中各个数据的权不同,即重要程度不同时,选择加权平均数能更好地反映这组数据的平均水平。
总
结
归
纳
权的表现形式:
比例、百分比
你能体会到权的作用吗?
幸运3+1
分宜县某校拟招聘一名优秀数学老师,现有甲乙两名教师入围,学校将录取得分最高者,如果面试和笔试成绩的权分别为6和4,从他们的成绩看,你认为应该录取谁?
应试者 面试 笔试
甲 86 90
乙 92 83
幸
运
3
+
1
加2分
已知一组数据4,12,24的权数分别是50%,20%,30%,则这组数据的加权平均数是________ .
11.6
幸
运
3
+
1
加3分
恭喜你,直接通关!加1分
幸
运
3
+
1
一组数据为10,8, ,12,13,这组数据的平均数是10,则 的值为_________。
7
加2分
注:每项满分10分
课
堂
小
结
请同学们根据自己的表现,并依据表格提供信息,设计评分方案,看看谁的表现最棒!
知识掌握 解决问题 课堂表现
得分
权
成绩 课本第113页练习1、2
课
后
作
业
