初中数学人教版(2024)九年级上册第二十二章 二次函数单元测试(含简单答案)
文档属性
| 名称 | 初中数学人教版(2024)九年级上册第二十二章 二次函数单元测试(含简单答案) | 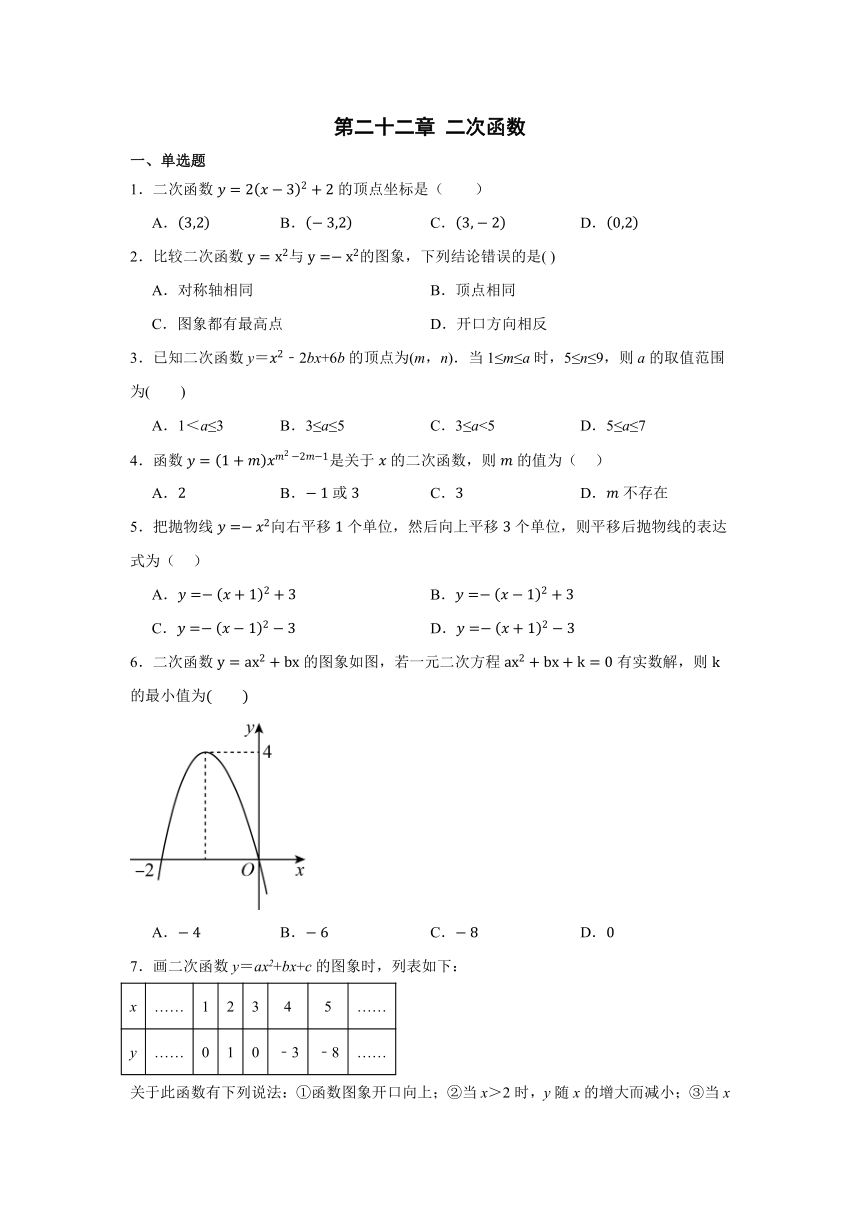 | |
| 格式 | docx | ||
| 文件大小 | 282.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-24 22:21:56 | ||
图片预览



文档简介
第二十二章 二次函数
一、单选题
1.二次函数的顶点坐标是( )
A. B. C. D.
2.比较二次函数与的图象,下列结论错误的是( )
A.对称轴相同 B.顶点相同
C.图象都有最高点 D.开口方向相反
3.已知二次函数y=﹣2bx+6b的顶点为(m,n).当1≤m≤a时,5≤n≤9,则a的取值范围为( )
A.1<a≤3 B.3≤a≤5 C.3≤a<5 D.5≤a≤7
4.函数是关于的二次函数,则的值为( )
A. B.或 C. D.不存在
5.把抛物线向右平移个单位,然后向上平移个单位,则平移后抛物线的表达式为( )
A. B.
C. D.
6.二次函数的图象如图,若一元二次方程有实数解,则k的最小值为
A. B. C. D.0
7.画二次函数y=ax2+bx+c的图象时,列表如下:
x …… 1 2 3 4 5 ……
y …… 0 1 0 ﹣3 ﹣8 ……
关于此函数有下列说法:①函数图象开口向上;②当x>2时,y随x的增大而减小;③当x=0时,y=﹣3;其中正确的是( )
A.①② B.①③ C.②③ D.①②③
8.如图所示,用长10m的铝合金条制成下部为矩形,上部为半圆的窗框(包括窗棂).若使此窗户的透光面积最大,则最大透光面积为()
A.50 B.50π C. D.
9.如图所示,已知二次函数的图象与轴交于两点,与轴交于点.对称轴为直线.直线与抛物线交于两点,点在轴下方且横坐标小于3,则下列结论:①;②;③;④.其中正确的有( )
A.4个 B.3个 C.2个 D.1个
10.如图,等腰直角△ABC中,斜边AB=4cm,动点P从A点从发,以1cm/s的速度向终点B匀速运动,过点P作AB的垂线交AC或BC边于点M,设P点运动的时间为x(s),△APM的面积为y,则y与x之间的函数关系的图象大致是( )
A. B.
C. D.
二、填空题
11.若二次函数y=x2﹣6x+3a的图象与x轴有且只有一个交点,则a的值为 .
12.抛物线y=x2向左平移1个单位,再向上平移5个单位所得函数解析式为 .
13.若点,,在二次函数的图像上,则,,的大小关系为 .(用“”连接)
14.学校有一个圆形喷水池,喷出的水流呈抛物线,一条水流的高度h(单位:m)与水流运动时间t(单位:s)之间的关系式为h=10t﹣t2,那么水流从喷出至回落到地面所需要的时间是 s.
15.抛物线y=x2+mx+(m﹣1)与x轴交于点A(x1,0),B(x2,0),x1<x2,与y轴交于点C,且满足x12+x22+x1x2=7,则△ABC的面积为 .
16.若抛物线(m是常数)与直线有两个不同的交点,且这两个交点在抛物线对称轴的同侧,则m的取值范围是 .
17.已知抛物线与轴的一个交点的横坐标大于1且小于2,则m的取值范围是 .
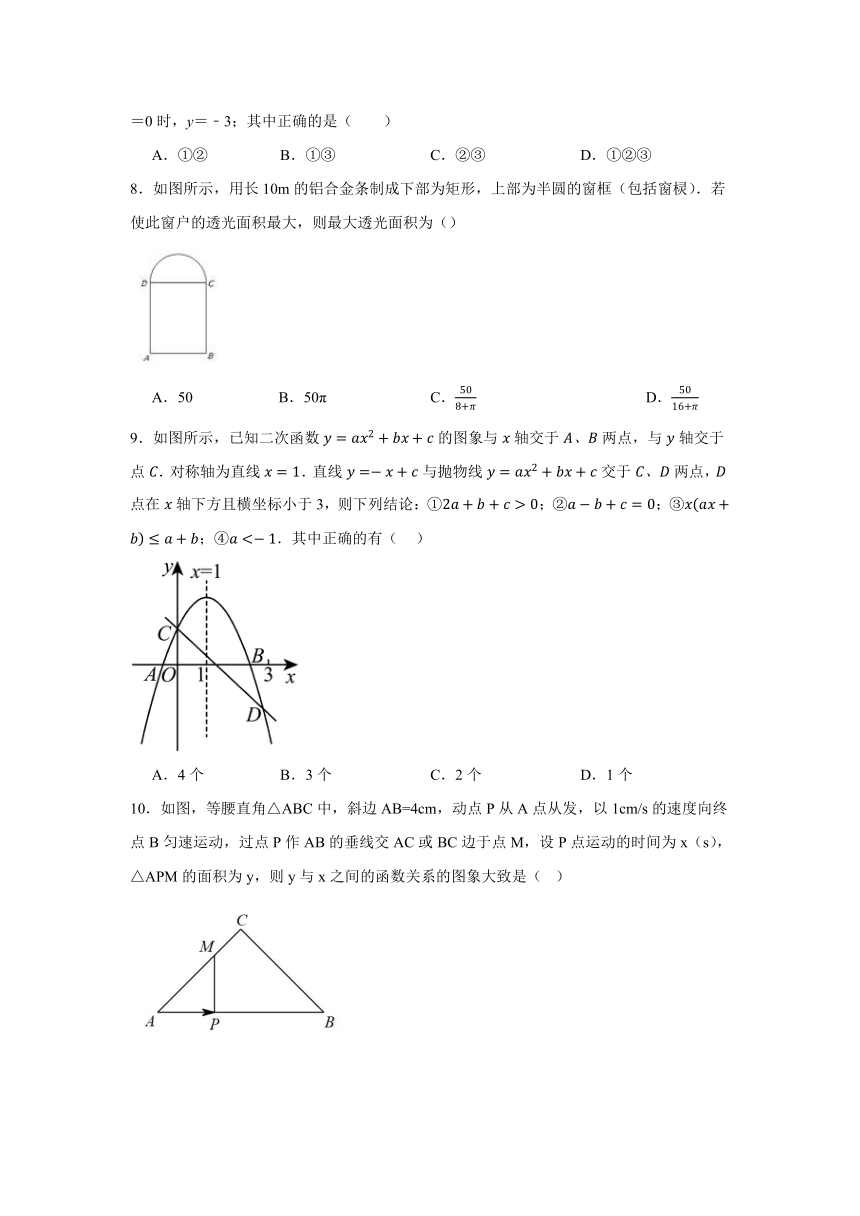
18.跳绳是大家喜爱的一项体育运动,当绳子甩到最高处时,其形状视为一条抛物线.如图是小冬与小雪将绳子甩到最高处时的示意图,并且相距4米,现以两人的站立点所在的直线为x轴,其中小冬拿绳子的手的坐标是.身高米的小丽站在绳子的正下方,且距y轴的距离为1米,绳子刚好经过她的头顶.若身高米的小伟站在这条绳子的正下方,他距y轴m米,则m的取值范围为 .
三、解答题
19.如图,在平面直角坐标系中,抛物线与x轴交于点、点,与y轴交于点C,点P是直线上一动点.
(1)求抛物线的解析式;
(2)过点P作轴,交抛物线于点Q,设的长度为,当h随m的增大而减小时,求出P的横坐标m的取值范围.
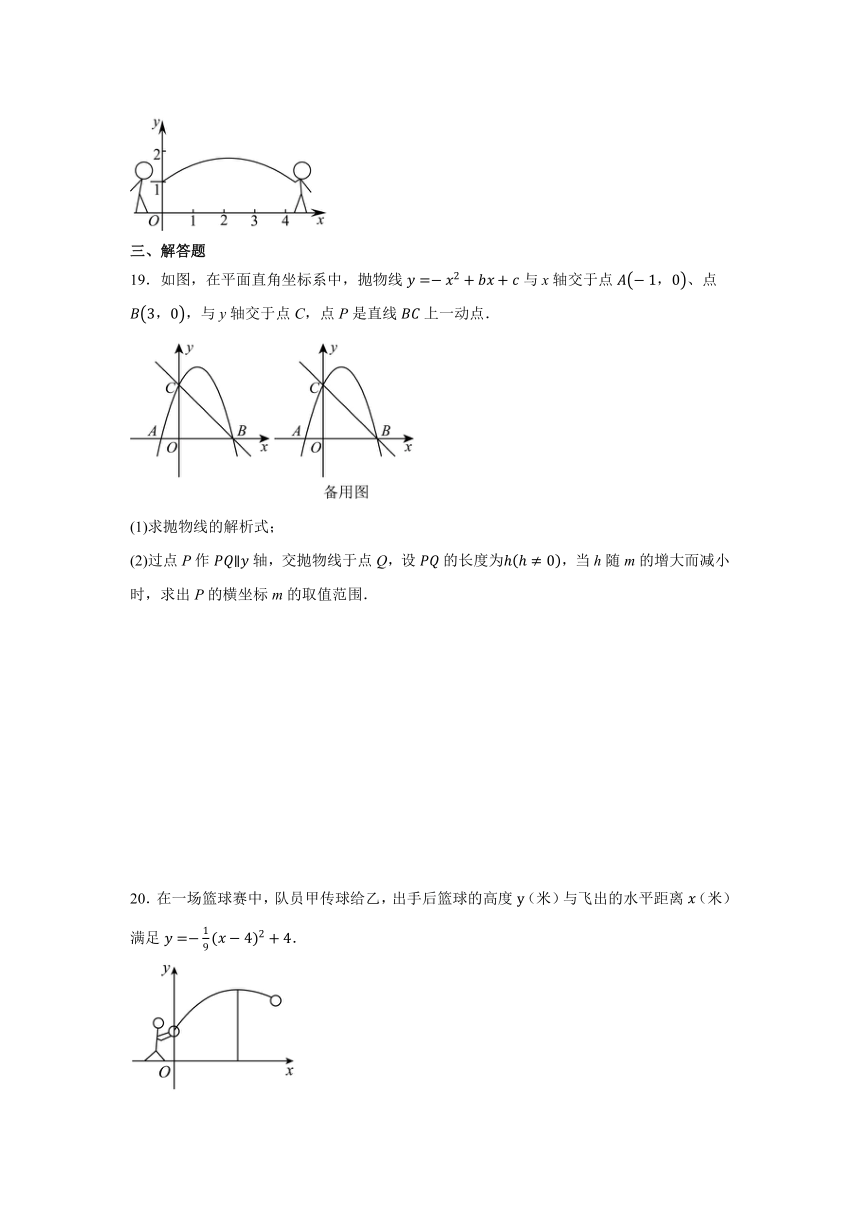
20.在一场篮球赛中,队员甲传球给乙,出手后篮球的高度(米)与飞出的水平距离(米)满足.
(1)这次传球的出手高度是________米,当篮球飞行的水平距离为________米时,达到最大高度,最大高度是________米;
(2)队员乙在篮球飞行方向上距甲6米处,他的最大摸高是3米,他在原地能接到球吗?如能接到,请计算说明;如不能他应该前进或后退多少米才能接到?
(3)球场界线在甲的传球方向前方9米处,如未能成功传球,篮球是否会出界?
21.为加强学生的素质教育,让学生看到自己的劳动成果,兴华中学围建了一个如图所示的矩形苗圃园让学生种菜.苗圃园其中一边靠墙,另外三边用长为的篱笆围成,已知墙长为,设这个苗圃园垂直于墙的一边的长为,这个苗圃园的面积为.
(1)求与之间的函数关系式;(直接写出的取值范围)
(2)当矩形场地的面积为时,求垂直于墙的一边的长;
(3)当取何值时这个苗圃园的面积最大,最大面积为多少?
22.如图,二次函数y=ax2+bx+c的图象与x轴相交于点A(﹣1,0)、B(3,0)两点,与y轴相交于点C(0,﹣3).
(1)求此二次函数的解析式;
(2)若抛物线的顶点为D,点E在抛物线上,且与点C关于抛物线的对称轴对称,直线AE交对称轴于点F,试判断四边形CDEF的形状,并证明你的结论.
23.如图,一小球从原点处抛出,球的抛出路线近似抛物线.若小球到达最高点的坐标为,.
(1)求抛物线的函数表达式;
(2)若要在斜坡上的点处竖直立一个高5米的广告牌,点的横坐标为3,请判断小球能否飞过这个广告牌?通过计算说明理由;
(3)计算小球在飞行的过程中距离斜坡的高度最大时与原点的水平距离是多少.
24.校园景观设计:如图1,学校计划在流经校园的小河上建造一座桥孔为抛物线的小桥,桥孔的跨径为8m,拱高为6m.
(1)把该桥孔看作一个二次函数的图像,建立适当的平面直角坐标系,写出这个二次函数的表达式;
(2)施工时,工人师傅先要制作如图2的桥孔模型,图中每个立柱之间距离相等,请你计算模型中左侧第二根立柱(AB)的高.
25.商店出售某品牌护眼灯,每台进价为40元,在销售过程中发现,月销量(台)与销售单价(元)之间满足一次函数关系,规定销售单价不低于进价,且不高于进价的2倍,其部分对应数据如下表所示:
销售单价(元) … 50 60 70 …
月销量(台) … 90 80 70 …
(1)求y与x之间的函数关系式;
(2)当护眼灯销售单价定为多少元时,商店每月出售这种护眼灯所获的利润最大?最大月利润为多少元?
26.在平面直角坐标系中,抛物线(a为常数,)与y轴交于点.
(1)求抛物线的解析式;
(2)将抛物线记为,将抛物线 记为,与合起来的图象记为L.对于L上的两点和,当,时,总有,求t的取值范围.
参考答案:
1.A
2.C
3.B
4.C
5.B
6.A
7.C
8.C
9.B
10.A
11.3
12.
13.
14.10.
15.1或6
16./
17.
18.
19.(1)
(2)或
20.(1)
(2)不能,他应该后退1米或前进5米
(3)篮球会出界
21.(1)
(2)
(3)当取时,最大面积为
22.(1)y=x2﹣2x﹣3
(2)正方形
23.(1)
(2)能飞过
(3)米
24.(1)(建系的方式不同,则答案不定)
(2)
25.(1)
(2)护眼灯销售单价定为80元时,商店每月出售这种护眼灯所获的利润最大,最大月利润为2400元
26.(1)
(2)或
一、单选题
1.二次函数的顶点坐标是( )
A. B. C. D.
2.比较二次函数与的图象,下列结论错误的是( )
A.对称轴相同 B.顶点相同
C.图象都有最高点 D.开口方向相反
3.已知二次函数y=﹣2bx+6b的顶点为(m,n).当1≤m≤a时,5≤n≤9,则a的取值范围为( )
A.1<a≤3 B.3≤a≤5 C.3≤a<5 D.5≤a≤7
4.函数是关于的二次函数,则的值为( )
A. B.或 C. D.不存在
5.把抛物线向右平移个单位,然后向上平移个单位,则平移后抛物线的表达式为( )
A. B.
C. D.
6.二次函数的图象如图,若一元二次方程有实数解,则k的最小值为
A. B. C. D.0
7.画二次函数y=ax2+bx+c的图象时,列表如下:
x …… 1 2 3 4 5 ……
y …… 0 1 0 ﹣3 ﹣8 ……
关于此函数有下列说法:①函数图象开口向上;②当x>2时,y随x的增大而减小;③当x=0时,y=﹣3;其中正确的是( )
A.①② B.①③ C.②③ D.①②③
8.如图所示,用长10m的铝合金条制成下部为矩形,上部为半圆的窗框(包括窗棂).若使此窗户的透光面积最大,则最大透光面积为()
A.50 B.50π C. D.
9.如图所示,已知二次函数的图象与轴交于两点,与轴交于点.对称轴为直线.直线与抛物线交于两点,点在轴下方且横坐标小于3,则下列结论:①;②;③;④.其中正确的有( )
A.4个 B.3个 C.2个 D.1个
10.如图,等腰直角△ABC中,斜边AB=4cm,动点P从A点从发,以1cm/s的速度向终点B匀速运动,过点P作AB的垂线交AC或BC边于点M,设P点运动的时间为x(s),△APM的面积为y,则y与x之间的函数关系的图象大致是( )
A. B.
C. D.
二、填空题
11.若二次函数y=x2﹣6x+3a的图象与x轴有且只有一个交点,则a的值为 .
12.抛物线y=x2向左平移1个单位,再向上平移5个单位所得函数解析式为 .
13.若点,,在二次函数的图像上,则,,的大小关系为 .(用“”连接)
14.学校有一个圆形喷水池,喷出的水流呈抛物线,一条水流的高度h(单位:m)与水流运动时间t(单位:s)之间的关系式为h=10t﹣t2,那么水流从喷出至回落到地面所需要的时间是 s.
15.抛物线y=x2+mx+(m﹣1)与x轴交于点A(x1,0),B(x2,0),x1<x2,与y轴交于点C,且满足x12+x22+x1x2=7,则△ABC的面积为 .
16.若抛物线(m是常数)与直线有两个不同的交点,且这两个交点在抛物线对称轴的同侧,则m的取值范围是 .
17.已知抛物线与轴的一个交点的横坐标大于1且小于2,则m的取值范围是 .
18.跳绳是大家喜爱的一项体育运动,当绳子甩到最高处时,其形状视为一条抛物线.如图是小冬与小雪将绳子甩到最高处时的示意图,并且相距4米,现以两人的站立点所在的直线为x轴,其中小冬拿绳子的手的坐标是.身高米的小丽站在绳子的正下方,且距y轴的距离为1米,绳子刚好经过她的头顶.若身高米的小伟站在这条绳子的正下方,他距y轴m米,则m的取值范围为 .
三、解答题
19.如图,在平面直角坐标系中,抛物线与x轴交于点、点,与y轴交于点C,点P是直线上一动点.
(1)求抛物线的解析式;
(2)过点P作轴,交抛物线于点Q,设的长度为,当h随m的增大而减小时,求出P的横坐标m的取值范围.
20.在一场篮球赛中,队员甲传球给乙,出手后篮球的高度(米)与飞出的水平距离(米)满足.
(1)这次传球的出手高度是________米,当篮球飞行的水平距离为________米时,达到最大高度,最大高度是________米;
(2)队员乙在篮球飞行方向上距甲6米处,他的最大摸高是3米,他在原地能接到球吗?如能接到,请计算说明;如不能他应该前进或后退多少米才能接到?
(3)球场界线在甲的传球方向前方9米处,如未能成功传球,篮球是否会出界?
21.为加强学生的素质教育,让学生看到自己的劳动成果,兴华中学围建了一个如图所示的矩形苗圃园让学生种菜.苗圃园其中一边靠墙,另外三边用长为的篱笆围成,已知墙长为,设这个苗圃园垂直于墙的一边的长为,这个苗圃园的面积为.
(1)求与之间的函数关系式;(直接写出的取值范围)
(2)当矩形场地的面积为时,求垂直于墙的一边的长;
(3)当取何值时这个苗圃园的面积最大,最大面积为多少?
22.如图,二次函数y=ax2+bx+c的图象与x轴相交于点A(﹣1,0)、B(3,0)两点,与y轴相交于点C(0,﹣3).
(1)求此二次函数的解析式;
(2)若抛物线的顶点为D,点E在抛物线上,且与点C关于抛物线的对称轴对称,直线AE交对称轴于点F,试判断四边形CDEF的形状,并证明你的结论.
23.如图,一小球从原点处抛出,球的抛出路线近似抛物线.若小球到达最高点的坐标为,.
(1)求抛物线的函数表达式;
(2)若要在斜坡上的点处竖直立一个高5米的广告牌,点的横坐标为3,请判断小球能否飞过这个广告牌?通过计算说明理由;
(3)计算小球在飞行的过程中距离斜坡的高度最大时与原点的水平距离是多少.
24.校园景观设计:如图1,学校计划在流经校园的小河上建造一座桥孔为抛物线的小桥,桥孔的跨径为8m,拱高为6m.
(1)把该桥孔看作一个二次函数的图像,建立适当的平面直角坐标系,写出这个二次函数的表达式;
(2)施工时,工人师傅先要制作如图2的桥孔模型,图中每个立柱之间距离相等,请你计算模型中左侧第二根立柱(AB)的高.
25.商店出售某品牌护眼灯,每台进价为40元,在销售过程中发现,月销量(台)与销售单价(元)之间满足一次函数关系,规定销售单价不低于进价,且不高于进价的2倍,其部分对应数据如下表所示:
销售单价(元) … 50 60 70 …
月销量(台) … 90 80 70 …
(1)求y与x之间的函数关系式;
(2)当护眼灯销售单价定为多少元时,商店每月出售这种护眼灯所获的利润最大?最大月利润为多少元?
26.在平面直角坐标系中,抛物线(a为常数,)与y轴交于点.
(1)求抛物线的解析式;
(2)将抛物线记为,将抛物线 记为,与合起来的图象记为L.对于L上的两点和,当,时,总有,求t的取值范围.
参考答案:
1.A
2.C
3.B
4.C
5.B
6.A
7.C
8.C
9.B
10.A
11.3
12.
13.
14.10.
15.1或6
16./
17.
18.
19.(1)
(2)或
20.(1)
(2)不能,他应该后退1米或前进5米
(3)篮球会出界
21.(1)
(2)
(3)当取时,最大面积为
22.(1)y=x2﹣2x﹣3
(2)正方形
23.(1)
(2)能飞过
(3)米
24.(1)(建系的方式不同,则答案不定)
(2)
25.(1)
(2)护眼灯销售单价定为80元时,商店每月出售这种护眼灯所获的利润最大,最大月利润为2400元
26.(1)
(2)或
同课章节目录
