福建省龙岩市2023-2024学年高一下学期7月期末考试 数学试题(含答案)
文档属性
| 名称 | 福建省龙岩市2023-2024学年高一下学期7月期末考试 数学试题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 756.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-25 00:00:00 | ||
图片预览



文档简介
龙岩市2023-2024学年高一下学期7月期末考试
数学试题
(考试时间:120分钟 满分:150分)
注意事项:
1.考生将自己的姓名、准考证号及所有的答案均填写在答题卡上.
2.答题要求见答题卡上的“填涂样例”和“注意事项”.
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 若圆锥的母线长为2,其侧面积为,则该圆锥的底面半径为( )
A. 2 B. C. D. 1
2. 若复数,则的虚部为( )
A. i B. 1 C. D.
3. 某人有3把钥匙,其中只有1把能打开门,若随机地取一把钥匙试着开门,把不能开门的钥匙扔掉,则第二次才能打开门的概率为( )
A. B. C. D.
4. 已知m,n是两条不同的直线,是两个不同的平面,下列命题错误的是( )
A. 若,,则
B. 若,,则
C. 若,,,则
D. 若,,则m与所成角和n与所成的角相等
5. 为了迎接2025年第九届亚冬会的召开,某班组织全班学生开展有关亚冬会知识的竞赛活动.已知该班男生30人,女生20人.按照分层抽样的方法从该班共抽取10人,进行一轮答题.相关统计情况如下:男生答对题目的平均数为10,方差为1;女生答对题目的平均数为15,方差为0.5,则这10人答对题目的方差为( )
A. 6.8 B. 6.9 C. 7 D. 7.2
6. 在中,内角A,B,C的对边分别为a,b,c,,若的面积为,则( )
A. B. C. D.
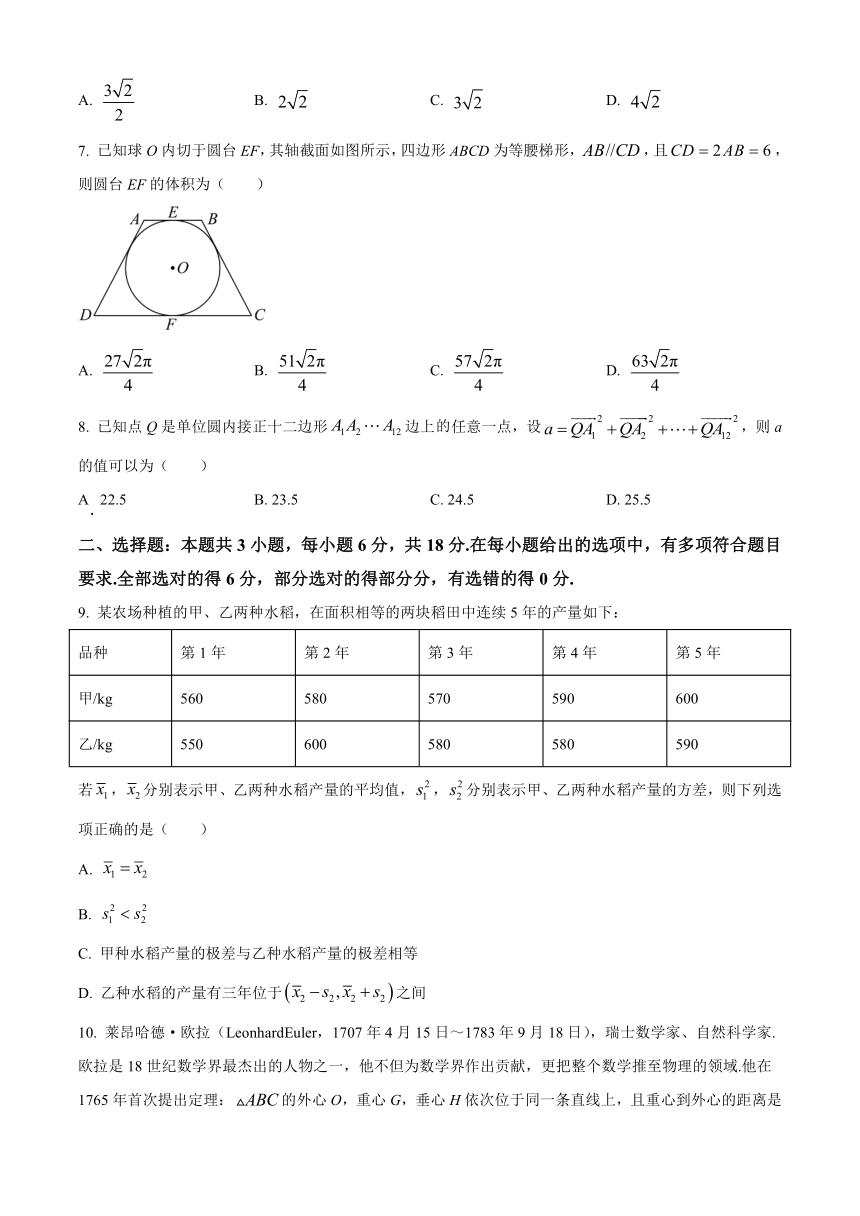
7. 已知球O内切于圆台EF,其轴截面如图所示,四边形ABCD为等腰梯形,,且,则圆台EF的体积为( )
A. B. C. D.
8. 已知点Q是单位圆内接正十二边形边上任意一点,设,则a的值可以为( )
A 22.5 B. 23.5 C. 24.5 D. 25.5
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9. 某农场种植的甲、乙两种水稻,在面积相等的两块稻田中连续5年的产量如下:
品种 第1年 第2年 第3年 第4年 第5年
甲/kg 560 580 570 590 600
乙/kg 550 600 580 580 590
若,分别表示甲、乙两种水稻产量的平均值,,分别表示甲、乙两种水稻产量的方差,则下列选项正确的是( )
A.
B.
C. 甲种水稻产量的极差与乙种水稻产量的极差相等
D. 乙种水稻的产量有三年位于之间
10. 莱昂哈德·欧拉(LeonhardEuler,1707年4月15日~1783年9月18日),瑞士数学家、自然科学家.欧拉是18世纪数学界最杰出的人物之一,他不但为数学界作出贡献,更把整个数学推至物理的领域.他在1765年首次提出定理:的外心O,重心G,垂心H依次位于同一条直线上,且重心到外心的距离是重心到垂心距离的一半,该直线被称为欧拉线.若,,则下列结论正确的是( )
A. B.
C. D.
11. 如图,在菱形ABCD中,M,N分别为棱AB,CD动点(不含端点),将菱形ABCD沿对角线BD折起,使点A不在平面BCD内.在翻折的过程中,下列结论正确的有( )
A. 若,则存在点M,N,使得MN与BC垂直
B. 对任意点M,存在点N,使得与,共面
C. 对任意点M,存在点N,使得MN与AD,BC所成的角相等
D. 若存在某个位置,使得直线AB与直线CD垂直,则一定为锐角
三、填空题:本题共3小题,每小题5分,共15分.
12. 若虚数i是方程的一个根,则______.
13. 设样本空间含有等可能的样本点,若事件A,B,C是的子集,且A,B,C两两独立,其中,,,,则______.
14. 空间四边形ABCD的四个顶点都在同一球面上,若,,,,空间四边形ABCD的体积为,它的外接球体积为,则的最大值为______.
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15. 已知是同一平面内的三个向量,其中.
(1)若,且,求;
(2)若的夹角为,,求在上的投影向量的坐标.
16. 为了解某工厂生产的产品尺寸情况,通过抽样,得到200件产品的尺寸(单位:mm)的数据,其频率分布直方图如图所示.
(1)求图中x的值,并根据频率分布直方图,估计这200件产品尺寸的平均数和上四分位数(同一组中的数据用该组区间的中点值代表,结果保留两位小数);
(2)记尺寸在内的产品为优等品,每件可获利5元;尺寸在内的产品为不合格品,每件亏损2元;其余尺寸的产品为合格品,每件可获利3元.若此工厂某月生产5000件产品,当该月利润未能达到15000元,则需要对该工厂设备实施升级改造.用样本的频率代替总体在各组的频率,试判断是否需要对该工厂设备实施升级改造.
17. 如图,在一条无限长的轨道上,一个质点最初位于位置0,规定:每次投掷一枚质地均匀的硬币,若正面向上,则质点向右移动一个单位,若反面向上,则质点向左移动一个单位,设投掷n次硬币后,质点位于位置.
(1)请直接写出和的数值;
(2)求;
(3)用a表示质点向右移动一个单位,用b表示质点向左移动一个单位,请写出投掷4次硬币的样本空间,并证明:.
18. 在中,内角A,B,C的对边分别为,,,且.
(1)求;
(2)设外接圆的半径为1,圆心为,为圆上异于点的一个动点.
(i)若,求证:四边形为等腰梯形;
(ii)若,求的取值范围.
19. 如图,在几何体中,四边形ABEF为正方形,,.记二面角大小为,二面角的大小为.
(1)证明:;
(2)若,且.
(i)求直线BD与平面CBE所成角的正弦值;
(ii)作出二面角的平面角,说明理由并求的值.
参考答案
1. B.
2. C
3. B.
4. C
5. A.
6. C
7. D.
8. B
9. ABD
10. AC.
11. BCD
12. 1
13.
14.
15. (1)
(2)
16. (1),平均数为99.64,上四分位数为102.14,
(2)不需要对该工厂设备实施升级改造,利用见解析
17. (1),,
(2)
(3)证明:掷4次硬币的样本空间为:
包含的样本点有
所以;
包含的样本点有
所以;
故,
18. (1)
(2)(i)证明;由正弦定理,则或,又,故,
则,故为外接圆直径,为中点,
又,故为等边三角形,故,
又,则,故,
又,则四边形为菱形,则,
故,故四边形为等腰梯形;
(ii)
19. (1)证明 在以,,,,,为顶点的五面体中,
,,平面,
平面.又平面,故
(2)(i)
(ii)由于平面,平面,故平面平面
过作,过作,连接,
则为二面角的平面角,
理由:,平面,平面平面,
故平面,平面,故,
又,平面,
故平面,平面,故,
故为二面角的平面角,
由于,所以,,
又,故,
数学试题
(考试时间:120分钟 满分:150分)
注意事项:
1.考生将自己的姓名、准考证号及所有的答案均填写在答题卡上.
2.答题要求见答题卡上的“填涂样例”和“注意事项”.
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 若圆锥的母线长为2,其侧面积为,则该圆锥的底面半径为( )
A. 2 B. C. D. 1
2. 若复数,则的虚部为( )
A. i B. 1 C. D.
3. 某人有3把钥匙,其中只有1把能打开门,若随机地取一把钥匙试着开门,把不能开门的钥匙扔掉,则第二次才能打开门的概率为( )
A. B. C. D.
4. 已知m,n是两条不同的直线,是两个不同的平面,下列命题错误的是( )
A. 若,,则
B. 若,,则
C. 若,,,则
D. 若,,则m与所成角和n与所成的角相等
5. 为了迎接2025年第九届亚冬会的召开,某班组织全班学生开展有关亚冬会知识的竞赛活动.已知该班男生30人,女生20人.按照分层抽样的方法从该班共抽取10人,进行一轮答题.相关统计情况如下:男生答对题目的平均数为10,方差为1;女生答对题目的平均数为15,方差为0.5,则这10人答对题目的方差为( )
A. 6.8 B. 6.9 C. 7 D. 7.2
6. 在中,内角A,B,C的对边分别为a,b,c,,若的面积为,则( )
A. B. C. D.
7. 已知球O内切于圆台EF,其轴截面如图所示,四边形ABCD为等腰梯形,,且,则圆台EF的体积为( )
A. B. C. D.
8. 已知点Q是单位圆内接正十二边形边上任意一点,设,则a的值可以为( )
A 22.5 B. 23.5 C. 24.5 D. 25.5
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9. 某农场种植的甲、乙两种水稻,在面积相等的两块稻田中连续5年的产量如下:
品种 第1年 第2年 第3年 第4年 第5年
甲/kg 560 580 570 590 600
乙/kg 550 600 580 580 590
若,分别表示甲、乙两种水稻产量的平均值,,分别表示甲、乙两种水稻产量的方差,则下列选项正确的是( )
A.
B.
C. 甲种水稻产量的极差与乙种水稻产量的极差相等
D. 乙种水稻的产量有三年位于之间
10. 莱昂哈德·欧拉(LeonhardEuler,1707年4月15日~1783年9月18日),瑞士数学家、自然科学家.欧拉是18世纪数学界最杰出的人物之一,他不但为数学界作出贡献,更把整个数学推至物理的领域.他在1765年首次提出定理:的外心O,重心G,垂心H依次位于同一条直线上,且重心到外心的距离是重心到垂心距离的一半,该直线被称为欧拉线.若,,则下列结论正确的是( )
A. B.
C. D.
11. 如图,在菱形ABCD中,M,N分别为棱AB,CD动点(不含端点),将菱形ABCD沿对角线BD折起,使点A不在平面BCD内.在翻折的过程中,下列结论正确的有( )
A. 若,则存在点M,N,使得MN与BC垂直
B. 对任意点M,存在点N,使得与,共面
C. 对任意点M,存在点N,使得MN与AD,BC所成的角相等
D. 若存在某个位置,使得直线AB与直线CD垂直,则一定为锐角
三、填空题:本题共3小题,每小题5分,共15分.
12. 若虚数i是方程的一个根,则______.
13. 设样本空间含有等可能的样本点,若事件A,B,C是的子集,且A,B,C两两独立,其中,,,,则______.
14. 空间四边形ABCD的四个顶点都在同一球面上,若,,,,空间四边形ABCD的体积为,它的外接球体积为,则的最大值为______.
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15. 已知是同一平面内的三个向量,其中.
(1)若,且,求;
(2)若的夹角为,,求在上的投影向量的坐标.
16. 为了解某工厂生产的产品尺寸情况,通过抽样,得到200件产品的尺寸(单位:mm)的数据,其频率分布直方图如图所示.
(1)求图中x的值,并根据频率分布直方图,估计这200件产品尺寸的平均数和上四分位数(同一组中的数据用该组区间的中点值代表,结果保留两位小数);
(2)记尺寸在内的产品为优等品,每件可获利5元;尺寸在内的产品为不合格品,每件亏损2元;其余尺寸的产品为合格品,每件可获利3元.若此工厂某月生产5000件产品,当该月利润未能达到15000元,则需要对该工厂设备实施升级改造.用样本的频率代替总体在各组的频率,试判断是否需要对该工厂设备实施升级改造.
17. 如图,在一条无限长的轨道上,一个质点最初位于位置0,规定:每次投掷一枚质地均匀的硬币,若正面向上,则质点向右移动一个单位,若反面向上,则质点向左移动一个单位,设投掷n次硬币后,质点位于位置.
(1)请直接写出和的数值;
(2)求;
(3)用a表示质点向右移动一个单位,用b表示质点向左移动一个单位,请写出投掷4次硬币的样本空间,并证明:.
18. 在中,内角A,B,C的对边分别为,,,且.
(1)求;
(2)设外接圆的半径为1,圆心为,为圆上异于点的一个动点.
(i)若,求证:四边形为等腰梯形;
(ii)若,求的取值范围.
19. 如图,在几何体中,四边形ABEF为正方形,,.记二面角大小为,二面角的大小为.
(1)证明:;
(2)若,且.
(i)求直线BD与平面CBE所成角的正弦值;
(ii)作出二面角的平面角,说明理由并求的值.
参考答案
1. B.
2. C
3. B.
4. C
5. A.
6. C
7. D.
8. B
9. ABD
10. AC.
11. BCD
12. 1
13.
14.
15. (1)
(2)
16. (1),平均数为99.64,上四分位数为102.14,
(2)不需要对该工厂设备实施升级改造,利用见解析
17. (1),,
(2)
(3)证明:掷4次硬币的样本空间为:
包含的样本点有
所以;
包含的样本点有
所以;
故,
18. (1)
(2)(i)证明;由正弦定理,则或,又,故,
则,故为外接圆直径,为中点,
又,故为等边三角形,故,
又,则,故,
又,则四边形为菱形,则,
故,故四边形为等腰梯形;
(ii)
19. (1)证明 在以,,,,,为顶点的五面体中,
,,平面,
平面.又平面,故
(2)(i)
(ii)由于平面,平面,故平面平面
过作,过作,连接,
则为二面角的平面角,
理由:,平面,平面平面,
故平面,平面,故,
又,平面,
故平面,平面,故,
故为二面角的平面角,
由于,所以,,
又,故,
同课章节目录
