2024年陕西省西安三中中考数学六模试卷(含答案)
文档属性
| 名称 | 2024年陕西省西安三中中考数学六模试卷(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 591.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-25 00:00:00 | ||
图片预览




文档简介
2024年陕西省西安三中中考数学六模试卷
一、选择题(共8小题,每小题3分,计24分每小题只有一个选项符合题意)
1.(3分)手机移动支付给生活带来便捷,若张阿姨微信收入5元表示为+5元,则张阿姨微信支出3元应表示为( )
A.﹣3元 B.+3元 C.﹣8元 D.+2元
2.(3分)如图所示的是某几何体的三视图,则该几何体的形状是( )
A.长方体 B.三棱柱 C.圆锥 D.正方体
3.(3分)化简(﹣3x3)2 2x所得的结果等于( )
A.﹣6x6 B.6x6 C.﹣18x7 D.18x7
4.(3分)一个角的度数是42°46′,则它的余角的度数为( )
A.47°14′ B.47°54′ C.57°14′ D.37°54′
5.(3分)已知函数y=kx(k≠0,k为常数)的函数值y随x值的增大而减小,那么这个函数图象可能经过的点是( )
A.(0.5,1) B.(2,1) C.(﹣2,4) D.(﹣2,﹣2)
6.(3分)如图,在Rt△ABC中,∠C=90°,D、E分别为CA、CB的中点,AF平分∠BAC,交DE于点F,若AC=6,BC=8,则EF的长为( )
A.2 B.1 C.4 D.
7.(3分)如图,四边形ABCD是⊙O的内接四边形,BC=CD,∠C=120°,∠D=80°,则∠AOB的度数为( )
A.100° B.115° C.120° D.135°
8.(3分)在平面直角坐标系中,若抛物线y=x2+(n﹣2m)x+m﹣n与抛物线y=x2+(4m﹣6)x+2m﹣3关于y轴对称,则符合条件的m,n的值为( )
A.m=,n= B.m=,n=
C.m=0,n=3 D.m=3,n=0
二、填空题(共5小题,每小题3分,计15分)
9.(3分)方程x2﹣4x=0的解为 .
10.(3分)如图,在正六边形ABCDEF中,连接AC、CF,则∠ACF的度数为 .
11.(3分)我国南宋数学家杨辉在1261年所著的《详解九章算法》一书里出现了如图所示的表,即“杨辉三角”,这是数学史上一个伟大成就.如图中取一列数:1,3,6,10,…,记a1=1,a2=3,a3=6,a4=10…,那么a9的值是 .
12.(3分)如图,在平面直角坐标系中,菱形ABCD的点C坐标为(﹣3,0),点D坐标为(0,4),点E为菱形的对称中心,若反比例函数恰好经过点E,则k的值为 .
13.(3分)如图,在矩形ABCD中,AB=6,BC=8,O为矩形ABCD的对角线的交点,以D为圆心,半径为1作⊙D,P为⊙D上的一个动点,连接AP、OP,则△AOP面积的最大值为 .
三、解答题(共13小题,计81分,解答应写出过程)
14.(5分)计算:()﹣2﹣6sin30°﹣|﹣1|.
15.(5分)求不等式的最大整数解.
16.(5分)解分式方程:﹣1=.
17.(5分)如图,在Rt△ABC中,∠BAC=90°,请用尺规作图法在边BC上求作一点D,使得S△ABD=S△ACD.(保留作图痕迹,不写作法)
18.(5分)如图所示,A、D、B、E四点在同一条直线上,若BC=EF,∠A=∠EDF,∠E+∠CBE=180°.求证:AC=DF.
19.(5分)某学校用33000元购进甲、乙两种医用口罩共计1000盒,免费发放给全校师生,甲,乙两种口罩的售价分别是30元/盒,35元/盒,求甲、乙两种口罩各购进了多少盒?
20.(5分)中华文化,源远流长,在古典文学方面,明代许仲琳著的《封神演义》、清代李汝珍著的《镜花缘》、清代郭小亭著的《济公传》、清代无垢道人著的《八仙传》(分别记作A,B,C,D)是我国古代四大神话小说.小明准备利用课余时间阅读这四部小说.
(1)若小明随机选择其中一部进行阅读,则他选择《封神演义》的概率是 ;
(2)若小明随机选择其中两部进行阅读,请你用列表或画树状图的方法,求出小明选择《镜花缘》和《八仙传》的概率.
21.(6分)阳光明媚的一天,小明与同学计划测量学校周围一栋古建筑AB的高度,由于古建筑底部不可到达,他们在古建筑AB的影子顶端C处,直立一个长为2米的标杆DC,经测量标杆的影子CE长为1米,接下来他们沿着BE方向从E点出发走了9米到达点F处,利用无人机测得GF为12米,并用无人机在G处测得观测B点的俯角约为37°,求古建筑AB的高.(参考数据:tan53°≈,sin53°≈,cos53°≈)
22.(7分)某店商计划采购甲、乙两种不同型号的平板电脑共30台,两种型号的平板电脑每台进价和销售价格如表所示:
型号 甲 乙
每台进价/元 1600 2500
每台售价/元 2000 3000
设采购甲型平板电脑x台,全部售出后获利y元.
(1)求y与x的函数表达式;
(2)若要求采购甲型平板电脑数量不小于乙型的2倍,如何采购才能使得获利最大?最大利润为多少?
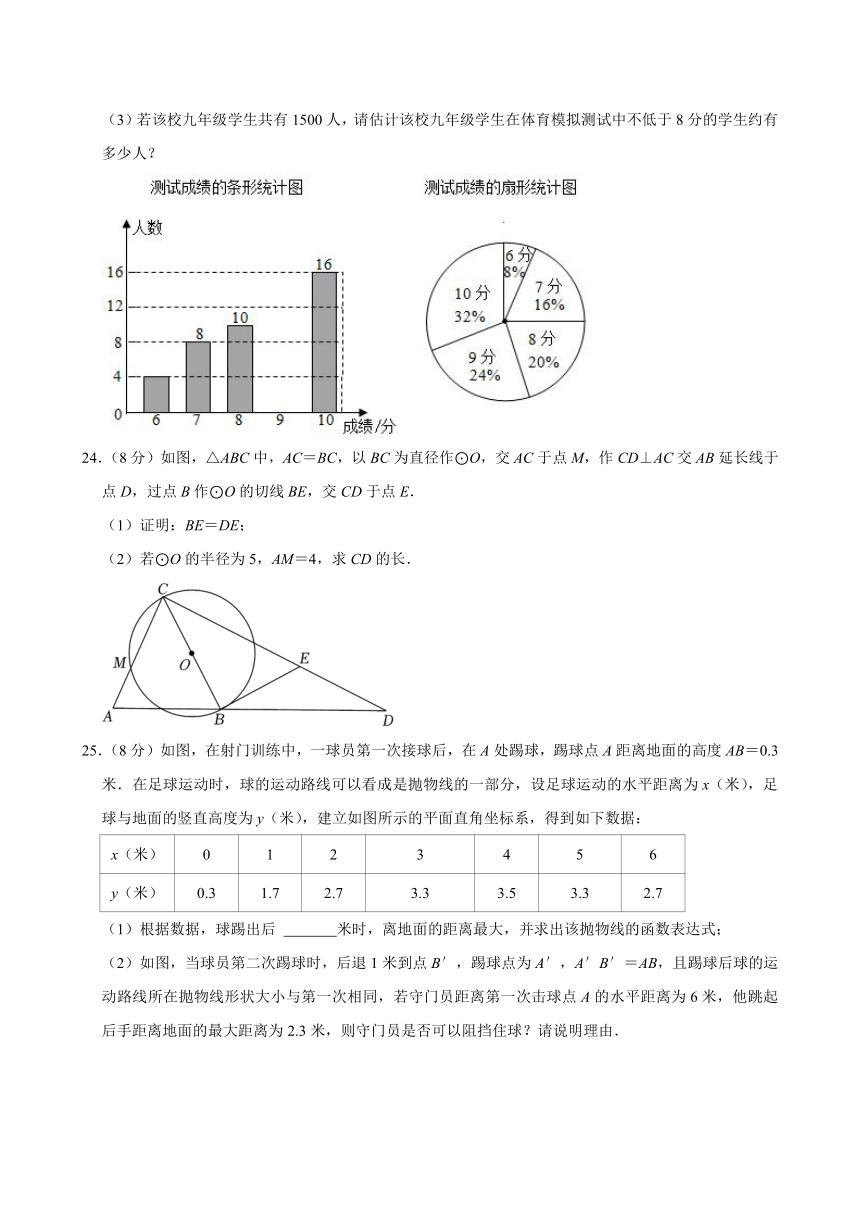
23.(7分)某校为了解九年级同学的体育考试准备情况,随机抽查该年级若干名学生进行体育模拟测试,根据测试成绩(单位:分)绘制成两幅不完整的统计图,请根据图中信息回答下面的问题:
(1)请补全条形统计图;
(2)所调查学生测试成绩的平均数为 ,中位数为 .众数为 ;
(3)若该校九年级学生共有1500人,请估计该校九年级学生在体育模拟测试中不低于8分的学生约有多少人?
24.(8分)如图,△ABC中,AC=BC,以BC为直径作⊙O,交AC于点M,作CD⊥AC交AB延长线于点D,过点B作⊙O的切线BE,交CD于点E.
(1)证明:BE=DE;
(2)若⊙O的半径为5,AM=4,求CD的长.
25.(8分)如图,在射门训练中,一球员第一次接球后,在A处踢球,踢球点A距离地面的高度AB=0.3米.在足球运动时,球的运动路线可以看成是抛物线的一部分,设足球运动的水平距离为x(米),足球与地面的竖直高度为y(米),建立如图所示的平面直角坐标系,得到如下数据:
x(米) 0 1 2 3 4 5 6
y(米) 0.3 1.7 2.7 3.3 3.5 3.3 2.7
(1)根据数据,球踢出后 米时,离地面的距离最大,并求出该抛物线的函数表达式;
(2)如图,当球员第二次踢球时,后退1米到点B′,踢球点为A′,A′B′=AB,且踢球后球的运动路线所在抛物线形状大小与第一次相同,若守门员距离第一次击球点A的水平距离为6米,他跳起后手距离地面的最大距离为2.3米,则守门员是否可以阻挡住球?请说明理由.
26.(10分)问题探究
(1)如图①,在△ABC中,AB=6,C是⊙O上任意一点,若⊙O的半径为2,点O到AB的距离为5,则△ABC面积的最大值为 .
问题解决
(2)如图②是一个矩形花园,AB=2千米,BD=4千米,聪聪给花园设计一种花卉种植方案:BCD内的点M处建一座凉亭,小路BD,BM,CM,DM将花园分成四个区域,用来种植不同,其中△CDM区域种植郁金香,小路CM改为一条玻璃观赏栈道.若∠CDM=∠DBM,是否点M,使得玻璃观赏栈道CM的值最小?若存在,请求出CM 的最小值及此时CDM的面不存在,请说明理由.
2024年陕西省西安三中中考数学六模试卷
参考答案
一、选择题(共8小题,每小题3分,计24分每小题只有一个选项符合题意)
1.(3分)手机移动支付给生活带来便捷,若张阿姨微信收入5元表示为+5元,则张阿姨微信支出3元应表示为( )
A.﹣3元 B.+3元 C.﹣8元 D.+2元
选:A.
2.(3分)如图所示的是某几何体的三视图,则该几何体的形状是( )
A.长方体 B.三棱柱 C.圆锥 D.正方体
选:B.
3.(3分)化简(﹣3x3)2 2x所得的结果等于( )
A.﹣6x6 B.6x6 C.﹣18x7 D.18x7
选:D.
4.(3分)一个角的度数是42°46′,则它的余角的度数为( )
A.47°14′ B.47°54′ C.57°14′ D.37°54′
选:A.
5.(3分)已知函数y=kx(k≠0,k为常数)的函数值y随x值的增大而减小,那么这个函数图象可能经过的点是( )
A.(0.5,1) B.(2,1) C.(﹣2,4) D.(﹣2,﹣2)
选:C.
6.(3分)如图,在Rt△ABC中,∠C=90°,D、E分别为CA、CB的中点,AF平分∠BAC,交DE于点F,若AC=6,BC=8,则EF的长为( )
A.2 B.1 C.4 D.
选:A.
7.(3分)如图,四边形ABCD是⊙O的内接四边形,BC=CD,∠C=120°,∠D=80°,则∠AOB的度数为( )
A.100° B.115° C.120° D.135°
选:A.
8.(3分)在平面直角坐标系中,若抛物线y=x2+(n﹣2m)x+m﹣n与抛物线y=x2+(4m﹣6)x+2m﹣3关于y轴对称,则符合条件的m,n的值为( )
A.m=,n= B.m=,n=
C.m=0,n=3 D.m=3,n=0
选:D.
二、填空题(共5小题,每小题3分,计15分)
9.(3分)方程x2﹣4x=0的解为 x1=0,x2=4 .
10.(3分)如图,在正六边形ABCDEF中,连接AC、CF,则∠ACF的度数为 30 .
11.(3分)我国南宋数学家杨辉在1261年所著的《详解九章算法》一书里出现了如图所示的表,即“杨辉三角”,这是数学史上一个伟大成就.如图中取一列数:1,3,6,10,…,记a1=1,a2=3,a3=6,a4=10…,那么a9的值是 45 .
12.(3分)如图,在平面直角坐标系中,菱形ABCD的点C坐标为(﹣3,0),点D坐标为(0,4),点E为菱形的对称中心,若反比例函数恰好经过点E,则k的值为 ﹣8 .
13.(3分)如图,在矩形ABCD中,AB=6,BC=8,O为矩形ABCD的对角线的交点,以D为圆心,半径为1作⊙D,P为⊙D上的一个动点,连接AP、OP,则△AOP面积的最大值为 14.5 .
三、解答题(共13小题,计81分,解答应写出过程)
14.(5分)计算:()﹣2﹣6sin30°﹣|﹣1|.
【解答】解:原式=﹣6×﹣(﹣1)
=﹣3﹣+1
=4﹣3﹣+1
=2﹣.
15.(5分)求不等式的最大整数解.
【解答】解:去分母,得:24﹣3(x﹣2)>2x,
去括号,得:24﹣3x+6>2x,
移项、合并同类项得:﹣5x>﹣30.
解得x<6,
则最大的整数解是:5.
16.(5分)解分式方程:﹣1=.
【解答】解:去分母得:x(x+2)﹣x2+4=1,
解得:x=﹣1.5,
经检验x=﹣1.5是分式方程的解.
17.(5分)如图,在Rt△ABC中,∠BAC=90°,请用尺规作图法在边BC上求作一点D,使得S△ABD=S△ACD.(保留作图痕迹,不写作法)
【解答】解:如图,点D即为所求.
18.(5分)如图所示,A、D、B、E四点在同一条直线上,若BC=EF,∠A=∠EDF,∠E+∠CBE=180°.求证:AC=DF.
【解答】证明:∵∠ABC+∠CBE=180°,∠E+∠CBE=180°.
∴∠ABC=∠E,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(AAS),
∴AC=DF.
19.(5分)某学校用33000元购进甲、乙两种医用口罩共计1000盒,免费发放给全校师生,甲,乙两种口罩的售价分别是30元/盒,35元/盒,求甲、乙两种口罩各购进了多少盒?
【解答】解:设学校购进甲种口罩x盒,购进乙种口罩y盒,
依题意,得:,
解得:.
答:学校购进甲种口罩400盒,购进乙种口罩600盒.
20.(5分)中华文化,源远流长,在古典文学方面,明代许仲琳著的《封神演义》、清代李汝珍著的《镜花缘》、清代郭小亭著的《济公传》、清代无垢道人著的《八仙传》(分别记作A,B,C,D)是我国古代四大神话小说.小明准备利用课余时间阅读这四部小说.
(1)若小明随机选择其中一部进行阅读,则他选择《封神演义》的概率是 ;
(2)若小明随机选择其中两部进行阅读,请你用列表或画树状图的方法,求出小明选择《镜花缘》和《八仙传》的概率.
【解答】解:(1)由题意知,共有4种等可能的结果,其中他选择《封神演义》的结果有1种,
∴他选择《封神演义》的概率是.
故答案为:.
(2)列表如下:
A B C D
A (A,B) (A,C) (A,D)
B (B,A) (B,C) (B,D)
C (C,A) (C,B) (C,D)
D (D,A) (D,B) (D,C)
共有12种等可能的结果,其中小明选择《镜花缘》和《八仙传》的结果有:(B,D),(D,B),共2种,
∴小明选择《镜花缘》和《八仙传》的概率为=.
21.(6分)阳光明媚的一天,小明与同学计划测量学校周围一栋古建筑AB的高度,由于古建筑底部不可到达,他们在古建筑AB的影子顶端C处,直立一个长为2米的标杆DC,经测量标杆的影子CE长为1米,接下来他们沿着BE方向从E点出发走了9米到达点F处,利用无人机测得GF为12米,并用无人机在G处测得观测B点的俯角约为37°,求古建筑AB的高.(参考数据:tan53°≈,sin53°≈,cos53°≈)
【解答】解:由题意,知∠BGF=90°﹣37°=53°,
在Rt△BGF中,
GF=12,∠BGF=53°,
∵tan∠BGF=,
∴BF=GFtan∠BGF=12tan53°=12×=16,
∴BC=BF﹣CE﹣EF=16﹣1﹣9=6,
∵太阳光线是平行光线,
∴AC∥DE,
∴∠ACB=∠DEC,
∵∠ABC=∠DCE=90°,
∴△ABC∽△DCE,
∴,
即,
解得AB=12.
答:古建筑AB的高为12米.
22.(7分)某店商计划采购甲、乙两种不同型号的平板电脑共30台,两种型号的平板电脑每台进价和销售价格如表所示:
型号 甲 乙
每台进价/元 1600 2500
每台售价/元 2000 3000
设采购甲型平板电脑x台,全部售出后获利y元.
(1)求y与x的函数表达式;
(2)若要求采购甲型平板电脑数量不小于乙型的2倍,如何采购才能使得获利最大?最大利润为多少?
【解答】解:(1)由题意得:y=(2000﹣1600)x+(3000﹣2500)(30﹣x)=﹣100x+15000,
∴全部售出后该商店获利y与x之间函数表达式为y=﹣100x+15000;
(2)由题意得:x≥2(30﹣x),
解得:x≥20,
∴20≤x≤30,
∵y=﹣100x+15000,且﹣100<0,
∴y随x的增大而减小,
∴当x=20时,y有最大值,最大值=﹣100×20+15000=13000,
∴采购甲型电脑20台,乙型电脑10台时商店获得最大利润,最大利润是13000元.
23.(7分)某校为了解九年级同学的体育考试准备情况,随机抽查该年级若干名学生进行体育模拟测试,根据测试成绩(单位:分)绘制成两幅不完整的统计图,请根据图中信息回答下面的问题:
(1)请补全条形统计图;
(2)所调查学生测试成绩的平均数为 8.56 ,中位数为 9 .众数为 10 ;
(3)若该校九年级学生共有1500人,请估计该校九年级学生在体育模拟测试中不低于8分的学生约有多少人?
【解答】解:(1)抽样学生中成绩为8分的有10人,占抽样学生数的20%,
所以本次抽样人数为:10÷20%=50(人),
因为成绩9分的人数占抽样人数的24%,
所以抽样学生中成绩为9分的有:50×24%=12(人).
补全条形统计图如下:
(2)所调查学生测试成绩的平均数为:
=8.56;
把该组数据按从小到大的顺序排列后,第24、25个数都是9,所以该组数据的中位数为:9;
该组数据中,10分出现的次数最多,所以众数为:10.
故答案为:8.56,9,10.
(3)由扇形图知,抽样学生中成绩不少于8分的占:20%+24%+32%=76%,
所以该校九年级学生在体育模拟测试中不低于8分的学生约有:1500×76%=1140(人).
答:该校九年级学生在体育模拟测试中不低于8分的学生约有1140人.
24.(8分)如图,△ABC中,AC=BC,以BC为直径作⊙O,交AC于点M,作CD⊥AC交AB延长线于点D,过点B作⊙O的切线BE,交CD于点E.
(1)证明:BE=DE;
(2)若⊙O的半径为5,AM=4,求CD的长.
【解答】(1)证明:∵CD⊥AC,
∴∠A+∠D=90°,
∵BE与⊙O切于点B,
∴CB⊥BE,
∴∠CBA+∠EBD=90°,
∵AC=BC,
∴∠A=∠CBA,
∴∠EBD=∠D,
∴BE=DE;
(2)解:如图,连接MB,
∵BC是⊙O的直径,⊙O的半径为5,
∴BM⊥AC,BC=AC=2×5=10,
∵AM=4,
∴MC=AC﹣AM=10﹣4=6,
∴MB===8,
∵AC⊥CD,
∴MB∥DC,
∴∠MBC=∠BCE,
∵∠BMC=∠CBE=90°,
∴△BMC∽△CBE,
∴,
∴,
∴BE=,
∴DE=BE=,
∵过点B作⊙O的切线BE,
∴∠CBE=90°,
∵CE==,
∴.
25.(8分)如图,在射门训练中,一球员第一次接球后,在A处踢球,踢球点A距离地面的高度AB=0.3米.在足球运动时,球的运动路线可以看成是抛物线的一部分,设足球运动的水平距离为x(米),足球与地面的竖直高度为y(米),建立如图所示的平面直角坐标系,得到如下数据:
x(米) 0 1 2 3 4 5 6
y(米) 0.3 1.7 2.7 3.3 3.5 3.3 2.7
(1)根据数据,球踢出后 4 米时,离地面的距离最大,并求出该抛物线的函数表达式;
(2)如图,当球员第二次踢球时,后退1米到点B′,踢球点为A′,A′B′=AB,且踢球后球的运动路线所在抛物线形状大小与第一次相同,若守门员距离第一次击球点A的水平距离为6米,他跳起后手距离地面的最大距离为2.3米,则守门员是否可以阻挡住球?请说明理由.
【解答】解:(1)由题意,根据表格数据可得,抛物线的对称轴是直线x==4,
∴顶点为(4,3.5).
∴当球踢出后4米时,离地面距离最大为3.5米.
故答案为:4.
又由题意,可设抛物线为y=a(x﹣4)2+3.5,
且抛物线过点(0,0.3),
∴0.3=16a+3.5.
∴a=﹣.
∴该抛物线的函数表达式为y=﹣(x﹣4)2+3.5.
(2)守门员可以阻挡住球.理由如下:
由题意可得,后退1米后的解析式为y=﹣(x﹣4+1)2+3.5,即y=﹣(x﹣3)2+3.5,
又守门员的位置是(6,0),
∴当x=6时,y=﹣(6﹣3)2+3.5=﹣1.8+3.5=1.7<2.3.
∴守门员可以阻挡住球.
26.(10分)问题探究
(1)如图①,在△ABC中,AB=6,C是⊙O上任意一点,若⊙O的半径为2,点O到AB的距离为5,则△ABC面积的最大值为 21 .
问题解决
(2)如图②是一个矩形花园,AB=2千米,BD=4千米,聪聪给花园设计一种花卉种植方案:BCD内的点M处建一座凉亭,小路BD,BM,CM,DM将花园分成四个区域,用来种植不同,其中△CDM区域种植郁金香,小路CM改为一条玻璃观赏栈道.若∠CDM=∠DBM,是否点M,使得玻璃观赏栈道CM的值最小?若存在,请求出CM 的最小值及此时CDM的面不存在,请说明理由.
【解答】解:(1)如图,过点O作OD⊥AB于点D,延长DO交⊙O于点E,连接AE,BE,
当点C与点E重合时,△ABC的面积最大,
此时S△ABC=.
故答案为:21.
(2)存在.
理由如下:在Rt△ABD 中,∠A=90°,AB=2,BD=4,
∴∠ADB=30°,,
∴∠CDB=60°,
∴∠CDM+∠BDM=60°,
∵∠CDM=∠DBM,
∴∠BDM+∠DBM=60°,
∴∠BMD=120°,
由特殊角的三角函数值及边角关系得出∠BMD=120°,
设点O是△BMD外接圆的圆心,由定边BD及定角∠BMD=120°,作△BMD的外接圆,
连接OB,OC,OM,
则∠BOD=120°,
∵OB=OD,
∴∠OBD=∠ODB=30°,
∴点O在AD上,∠ABO=30°,在 Rt△ABO 中,AB=2,∠ABO=30°,
,
∴,
在Rt△OCD中,CD=2,,
∴OC==,
∵在△OCM中,CM+OM≥OC,
∴,
根据OM、OC的长,由三角形三边关系得出CM的最小值,
∴当O,C,M三点共线时,CM的值最小,
即CM的最小值为 .
此时点M在OC与⊙O的交点M'处,
∴,
过点M'作M′N⊥CD于点N,
∴∠CNM'=∠CDO=90°,
∴△CM′N∽△COD,
∴,
解得 ,
S△CDM'==,
∴存在点M,使得玻璃观赏栈道CM的值最小,最小值为 千米,
此时△CDM的面积为 平方千米.
一、选择题(共8小题,每小题3分,计24分每小题只有一个选项符合题意)
1.(3分)手机移动支付给生活带来便捷,若张阿姨微信收入5元表示为+5元,则张阿姨微信支出3元应表示为( )
A.﹣3元 B.+3元 C.﹣8元 D.+2元
2.(3分)如图所示的是某几何体的三视图,则该几何体的形状是( )
A.长方体 B.三棱柱 C.圆锥 D.正方体
3.(3分)化简(﹣3x3)2 2x所得的结果等于( )
A.﹣6x6 B.6x6 C.﹣18x7 D.18x7
4.(3分)一个角的度数是42°46′,则它的余角的度数为( )
A.47°14′ B.47°54′ C.57°14′ D.37°54′
5.(3分)已知函数y=kx(k≠0,k为常数)的函数值y随x值的增大而减小,那么这个函数图象可能经过的点是( )
A.(0.5,1) B.(2,1) C.(﹣2,4) D.(﹣2,﹣2)
6.(3分)如图,在Rt△ABC中,∠C=90°,D、E分别为CA、CB的中点,AF平分∠BAC,交DE于点F,若AC=6,BC=8,则EF的长为( )
A.2 B.1 C.4 D.
7.(3分)如图,四边形ABCD是⊙O的内接四边形,BC=CD,∠C=120°,∠D=80°,则∠AOB的度数为( )
A.100° B.115° C.120° D.135°
8.(3分)在平面直角坐标系中,若抛物线y=x2+(n﹣2m)x+m﹣n与抛物线y=x2+(4m﹣6)x+2m﹣3关于y轴对称,则符合条件的m,n的值为( )
A.m=,n= B.m=,n=
C.m=0,n=3 D.m=3,n=0
二、填空题(共5小题,每小题3分,计15分)
9.(3分)方程x2﹣4x=0的解为 .
10.(3分)如图,在正六边形ABCDEF中,连接AC、CF,则∠ACF的度数为 .
11.(3分)我国南宋数学家杨辉在1261年所著的《详解九章算法》一书里出现了如图所示的表,即“杨辉三角”,这是数学史上一个伟大成就.如图中取一列数:1,3,6,10,…,记a1=1,a2=3,a3=6,a4=10…,那么a9的值是 .
12.(3分)如图,在平面直角坐标系中,菱形ABCD的点C坐标为(﹣3,0),点D坐标为(0,4),点E为菱形的对称中心,若反比例函数恰好经过点E,则k的值为 .
13.(3分)如图,在矩形ABCD中,AB=6,BC=8,O为矩形ABCD的对角线的交点,以D为圆心,半径为1作⊙D,P为⊙D上的一个动点,连接AP、OP,则△AOP面积的最大值为 .
三、解答题(共13小题,计81分,解答应写出过程)
14.(5分)计算:()﹣2﹣6sin30°﹣|﹣1|.
15.(5分)求不等式的最大整数解.
16.(5分)解分式方程:﹣1=.
17.(5分)如图,在Rt△ABC中,∠BAC=90°,请用尺规作图法在边BC上求作一点D,使得S△ABD=S△ACD.(保留作图痕迹,不写作法)
18.(5分)如图所示,A、D、B、E四点在同一条直线上,若BC=EF,∠A=∠EDF,∠E+∠CBE=180°.求证:AC=DF.
19.(5分)某学校用33000元购进甲、乙两种医用口罩共计1000盒,免费发放给全校师生,甲,乙两种口罩的售价分别是30元/盒,35元/盒,求甲、乙两种口罩各购进了多少盒?
20.(5分)中华文化,源远流长,在古典文学方面,明代许仲琳著的《封神演义》、清代李汝珍著的《镜花缘》、清代郭小亭著的《济公传》、清代无垢道人著的《八仙传》(分别记作A,B,C,D)是我国古代四大神话小说.小明准备利用课余时间阅读这四部小说.
(1)若小明随机选择其中一部进行阅读,则他选择《封神演义》的概率是 ;
(2)若小明随机选择其中两部进行阅读,请你用列表或画树状图的方法,求出小明选择《镜花缘》和《八仙传》的概率.
21.(6分)阳光明媚的一天,小明与同学计划测量学校周围一栋古建筑AB的高度,由于古建筑底部不可到达,他们在古建筑AB的影子顶端C处,直立一个长为2米的标杆DC,经测量标杆的影子CE长为1米,接下来他们沿着BE方向从E点出发走了9米到达点F处,利用无人机测得GF为12米,并用无人机在G处测得观测B点的俯角约为37°,求古建筑AB的高.(参考数据:tan53°≈,sin53°≈,cos53°≈)
22.(7分)某店商计划采购甲、乙两种不同型号的平板电脑共30台,两种型号的平板电脑每台进价和销售价格如表所示:
型号 甲 乙
每台进价/元 1600 2500
每台售价/元 2000 3000
设采购甲型平板电脑x台,全部售出后获利y元.
(1)求y与x的函数表达式;
(2)若要求采购甲型平板电脑数量不小于乙型的2倍,如何采购才能使得获利最大?最大利润为多少?
23.(7分)某校为了解九年级同学的体育考试准备情况,随机抽查该年级若干名学生进行体育模拟测试,根据测试成绩(单位:分)绘制成两幅不完整的统计图,请根据图中信息回答下面的问题:
(1)请补全条形统计图;
(2)所调查学生测试成绩的平均数为 ,中位数为 .众数为 ;
(3)若该校九年级学生共有1500人,请估计该校九年级学生在体育模拟测试中不低于8分的学生约有多少人?
24.(8分)如图,△ABC中,AC=BC,以BC为直径作⊙O,交AC于点M,作CD⊥AC交AB延长线于点D,过点B作⊙O的切线BE,交CD于点E.
(1)证明:BE=DE;
(2)若⊙O的半径为5,AM=4,求CD的长.
25.(8分)如图,在射门训练中,一球员第一次接球后,在A处踢球,踢球点A距离地面的高度AB=0.3米.在足球运动时,球的运动路线可以看成是抛物线的一部分,设足球运动的水平距离为x(米),足球与地面的竖直高度为y(米),建立如图所示的平面直角坐标系,得到如下数据:
x(米) 0 1 2 3 4 5 6
y(米) 0.3 1.7 2.7 3.3 3.5 3.3 2.7
(1)根据数据,球踢出后 米时,离地面的距离最大,并求出该抛物线的函数表达式;
(2)如图,当球员第二次踢球时,后退1米到点B′,踢球点为A′,A′B′=AB,且踢球后球的运动路线所在抛物线形状大小与第一次相同,若守门员距离第一次击球点A的水平距离为6米,他跳起后手距离地面的最大距离为2.3米,则守门员是否可以阻挡住球?请说明理由.
26.(10分)问题探究
(1)如图①,在△ABC中,AB=6,C是⊙O上任意一点,若⊙O的半径为2,点O到AB的距离为5,则△ABC面积的最大值为 .
问题解决
(2)如图②是一个矩形花园,AB=2千米,BD=4千米,聪聪给花园设计一种花卉种植方案:BCD内的点M处建一座凉亭,小路BD,BM,CM,DM将花园分成四个区域,用来种植不同,其中△CDM区域种植郁金香,小路CM改为一条玻璃观赏栈道.若∠CDM=∠DBM,是否点M,使得玻璃观赏栈道CM的值最小?若存在,请求出CM 的最小值及此时CDM的面不存在,请说明理由.
2024年陕西省西安三中中考数学六模试卷
参考答案
一、选择题(共8小题,每小题3分,计24分每小题只有一个选项符合题意)
1.(3分)手机移动支付给生活带来便捷,若张阿姨微信收入5元表示为+5元,则张阿姨微信支出3元应表示为( )
A.﹣3元 B.+3元 C.﹣8元 D.+2元
选:A.
2.(3分)如图所示的是某几何体的三视图,则该几何体的形状是( )
A.长方体 B.三棱柱 C.圆锥 D.正方体
选:B.
3.(3分)化简(﹣3x3)2 2x所得的结果等于( )
A.﹣6x6 B.6x6 C.﹣18x7 D.18x7
选:D.
4.(3分)一个角的度数是42°46′,则它的余角的度数为( )
A.47°14′ B.47°54′ C.57°14′ D.37°54′
选:A.
5.(3分)已知函数y=kx(k≠0,k为常数)的函数值y随x值的增大而减小,那么这个函数图象可能经过的点是( )
A.(0.5,1) B.(2,1) C.(﹣2,4) D.(﹣2,﹣2)
选:C.
6.(3分)如图,在Rt△ABC中,∠C=90°,D、E分别为CA、CB的中点,AF平分∠BAC,交DE于点F,若AC=6,BC=8,则EF的长为( )
A.2 B.1 C.4 D.
选:A.
7.(3分)如图,四边形ABCD是⊙O的内接四边形,BC=CD,∠C=120°,∠D=80°,则∠AOB的度数为( )
A.100° B.115° C.120° D.135°
选:A.
8.(3分)在平面直角坐标系中,若抛物线y=x2+(n﹣2m)x+m﹣n与抛物线y=x2+(4m﹣6)x+2m﹣3关于y轴对称,则符合条件的m,n的值为( )
A.m=,n= B.m=,n=
C.m=0,n=3 D.m=3,n=0
选:D.
二、填空题(共5小题,每小题3分,计15分)
9.(3分)方程x2﹣4x=0的解为 x1=0,x2=4 .
10.(3分)如图,在正六边形ABCDEF中,连接AC、CF,则∠ACF的度数为 30 .
11.(3分)我国南宋数学家杨辉在1261年所著的《详解九章算法》一书里出现了如图所示的表,即“杨辉三角”,这是数学史上一个伟大成就.如图中取一列数:1,3,6,10,…,记a1=1,a2=3,a3=6,a4=10…,那么a9的值是 45 .
12.(3分)如图,在平面直角坐标系中,菱形ABCD的点C坐标为(﹣3,0),点D坐标为(0,4),点E为菱形的对称中心,若反比例函数恰好经过点E,则k的值为 ﹣8 .
13.(3分)如图,在矩形ABCD中,AB=6,BC=8,O为矩形ABCD的对角线的交点,以D为圆心,半径为1作⊙D,P为⊙D上的一个动点,连接AP、OP,则△AOP面积的最大值为 14.5 .
三、解答题(共13小题,计81分,解答应写出过程)
14.(5分)计算:()﹣2﹣6sin30°﹣|﹣1|.
【解答】解:原式=﹣6×﹣(﹣1)
=﹣3﹣+1
=4﹣3﹣+1
=2﹣.
15.(5分)求不等式的最大整数解.
【解答】解:去分母,得:24﹣3(x﹣2)>2x,
去括号,得:24﹣3x+6>2x,
移项、合并同类项得:﹣5x>﹣30.
解得x<6,
则最大的整数解是:5.
16.(5分)解分式方程:﹣1=.
【解答】解:去分母得:x(x+2)﹣x2+4=1,
解得:x=﹣1.5,
经检验x=﹣1.5是分式方程的解.
17.(5分)如图,在Rt△ABC中,∠BAC=90°,请用尺规作图法在边BC上求作一点D,使得S△ABD=S△ACD.(保留作图痕迹,不写作法)
【解答】解:如图,点D即为所求.
18.(5分)如图所示,A、D、B、E四点在同一条直线上,若BC=EF,∠A=∠EDF,∠E+∠CBE=180°.求证:AC=DF.
【解答】证明:∵∠ABC+∠CBE=180°,∠E+∠CBE=180°.
∴∠ABC=∠E,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(AAS),
∴AC=DF.
19.(5分)某学校用33000元购进甲、乙两种医用口罩共计1000盒,免费发放给全校师生,甲,乙两种口罩的售价分别是30元/盒,35元/盒,求甲、乙两种口罩各购进了多少盒?
【解答】解:设学校购进甲种口罩x盒,购进乙种口罩y盒,
依题意,得:,
解得:.
答:学校购进甲种口罩400盒,购进乙种口罩600盒.
20.(5分)中华文化,源远流长,在古典文学方面,明代许仲琳著的《封神演义》、清代李汝珍著的《镜花缘》、清代郭小亭著的《济公传》、清代无垢道人著的《八仙传》(分别记作A,B,C,D)是我国古代四大神话小说.小明准备利用课余时间阅读这四部小说.
(1)若小明随机选择其中一部进行阅读,则他选择《封神演义》的概率是 ;
(2)若小明随机选择其中两部进行阅读,请你用列表或画树状图的方法,求出小明选择《镜花缘》和《八仙传》的概率.
【解答】解:(1)由题意知,共有4种等可能的结果,其中他选择《封神演义》的结果有1种,
∴他选择《封神演义》的概率是.
故答案为:.
(2)列表如下:
A B C D
A (A,B) (A,C) (A,D)
B (B,A) (B,C) (B,D)
C (C,A) (C,B) (C,D)
D (D,A) (D,B) (D,C)
共有12种等可能的结果,其中小明选择《镜花缘》和《八仙传》的结果有:(B,D),(D,B),共2种,
∴小明选择《镜花缘》和《八仙传》的概率为=.
21.(6分)阳光明媚的一天,小明与同学计划测量学校周围一栋古建筑AB的高度,由于古建筑底部不可到达,他们在古建筑AB的影子顶端C处,直立一个长为2米的标杆DC,经测量标杆的影子CE长为1米,接下来他们沿着BE方向从E点出发走了9米到达点F处,利用无人机测得GF为12米,并用无人机在G处测得观测B点的俯角约为37°,求古建筑AB的高.(参考数据:tan53°≈,sin53°≈,cos53°≈)
【解答】解:由题意,知∠BGF=90°﹣37°=53°,
在Rt△BGF中,
GF=12,∠BGF=53°,
∵tan∠BGF=,
∴BF=GFtan∠BGF=12tan53°=12×=16,
∴BC=BF﹣CE﹣EF=16﹣1﹣9=6,
∵太阳光线是平行光线,
∴AC∥DE,
∴∠ACB=∠DEC,
∵∠ABC=∠DCE=90°,
∴△ABC∽△DCE,
∴,
即,
解得AB=12.
答:古建筑AB的高为12米.
22.(7分)某店商计划采购甲、乙两种不同型号的平板电脑共30台,两种型号的平板电脑每台进价和销售价格如表所示:
型号 甲 乙
每台进价/元 1600 2500
每台售价/元 2000 3000
设采购甲型平板电脑x台,全部售出后获利y元.
(1)求y与x的函数表达式;
(2)若要求采购甲型平板电脑数量不小于乙型的2倍,如何采购才能使得获利最大?最大利润为多少?
【解答】解:(1)由题意得:y=(2000﹣1600)x+(3000﹣2500)(30﹣x)=﹣100x+15000,
∴全部售出后该商店获利y与x之间函数表达式为y=﹣100x+15000;
(2)由题意得:x≥2(30﹣x),
解得:x≥20,
∴20≤x≤30,
∵y=﹣100x+15000,且﹣100<0,
∴y随x的增大而减小,
∴当x=20时,y有最大值,最大值=﹣100×20+15000=13000,
∴采购甲型电脑20台,乙型电脑10台时商店获得最大利润,最大利润是13000元.
23.(7分)某校为了解九年级同学的体育考试准备情况,随机抽查该年级若干名学生进行体育模拟测试,根据测试成绩(单位:分)绘制成两幅不完整的统计图,请根据图中信息回答下面的问题:
(1)请补全条形统计图;
(2)所调查学生测试成绩的平均数为 8.56 ,中位数为 9 .众数为 10 ;
(3)若该校九年级学生共有1500人,请估计该校九年级学生在体育模拟测试中不低于8分的学生约有多少人?
【解答】解:(1)抽样学生中成绩为8分的有10人,占抽样学生数的20%,
所以本次抽样人数为:10÷20%=50(人),
因为成绩9分的人数占抽样人数的24%,
所以抽样学生中成绩为9分的有:50×24%=12(人).
补全条形统计图如下:
(2)所调查学生测试成绩的平均数为:
=8.56;
把该组数据按从小到大的顺序排列后,第24、25个数都是9,所以该组数据的中位数为:9;
该组数据中,10分出现的次数最多,所以众数为:10.
故答案为:8.56,9,10.
(3)由扇形图知,抽样学生中成绩不少于8分的占:20%+24%+32%=76%,
所以该校九年级学生在体育模拟测试中不低于8分的学生约有:1500×76%=1140(人).
答:该校九年级学生在体育模拟测试中不低于8分的学生约有1140人.
24.(8分)如图,△ABC中,AC=BC,以BC为直径作⊙O,交AC于点M,作CD⊥AC交AB延长线于点D,过点B作⊙O的切线BE,交CD于点E.
(1)证明:BE=DE;
(2)若⊙O的半径为5,AM=4,求CD的长.
【解答】(1)证明:∵CD⊥AC,
∴∠A+∠D=90°,
∵BE与⊙O切于点B,
∴CB⊥BE,
∴∠CBA+∠EBD=90°,
∵AC=BC,
∴∠A=∠CBA,
∴∠EBD=∠D,
∴BE=DE;
(2)解:如图,连接MB,
∵BC是⊙O的直径,⊙O的半径为5,
∴BM⊥AC,BC=AC=2×5=10,
∵AM=4,
∴MC=AC﹣AM=10﹣4=6,
∴MB===8,
∵AC⊥CD,
∴MB∥DC,
∴∠MBC=∠BCE,
∵∠BMC=∠CBE=90°,
∴△BMC∽△CBE,
∴,
∴,
∴BE=,
∴DE=BE=,
∵过点B作⊙O的切线BE,
∴∠CBE=90°,
∵CE==,
∴.
25.(8分)如图,在射门训练中,一球员第一次接球后,在A处踢球,踢球点A距离地面的高度AB=0.3米.在足球运动时,球的运动路线可以看成是抛物线的一部分,设足球运动的水平距离为x(米),足球与地面的竖直高度为y(米),建立如图所示的平面直角坐标系,得到如下数据:
x(米) 0 1 2 3 4 5 6
y(米) 0.3 1.7 2.7 3.3 3.5 3.3 2.7
(1)根据数据,球踢出后 4 米时,离地面的距离最大,并求出该抛物线的函数表达式;
(2)如图,当球员第二次踢球时,后退1米到点B′,踢球点为A′,A′B′=AB,且踢球后球的运动路线所在抛物线形状大小与第一次相同,若守门员距离第一次击球点A的水平距离为6米,他跳起后手距离地面的最大距离为2.3米,则守门员是否可以阻挡住球?请说明理由.
【解答】解:(1)由题意,根据表格数据可得,抛物线的对称轴是直线x==4,
∴顶点为(4,3.5).
∴当球踢出后4米时,离地面距离最大为3.5米.
故答案为:4.
又由题意,可设抛物线为y=a(x﹣4)2+3.5,
且抛物线过点(0,0.3),
∴0.3=16a+3.5.
∴a=﹣.
∴该抛物线的函数表达式为y=﹣(x﹣4)2+3.5.
(2)守门员可以阻挡住球.理由如下:
由题意可得,后退1米后的解析式为y=﹣(x﹣4+1)2+3.5,即y=﹣(x﹣3)2+3.5,
又守门员的位置是(6,0),
∴当x=6时,y=﹣(6﹣3)2+3.5=﹣1.8+3.5=1.7<2.3.
∴守门员可以阻挡住球.
26.(10分)问题探究
(1)如图①,在△ABC中,AB=6,C是⊙O上任意一点,若⊙O的半径为2,点O到AB的距离为5,则△ABC面积的最大值为 21 .
问题解决
(2)如图②是一个矩形花园,AB=2千米,BD=4千米,聪聪给花园设计一种花卉种植方案:BCD内的点M处建一座凉亭,小路BD,BM,CM,DM将花园分成四个区域,用来种植不同,其中△CDM区域种植郁金香,小路CM改为一条玻璃观赏栈道.若∠CDM=∠DBM,是否点M,使得玻璃观赏栈道CM的值最小?若存在,请求出CM 的最小值及此时CDM的面不存在,请说明理由.
【解答】解:(1)如图,过点O作OD⊥AB于点D,延长DO交⊙O于点E,连接AE,BE,
当点C与点E重合时,△ABC的面积最大,
此时S△ABC=.
故答案为:21.
(2)存在.
理由如下:在Rt△ABD 中,∠A=90°,AB=2,BD=4,
∴∠ADB=30°,,
∴∠CDB=60°,
∴∠CDM+∠BDM=60°,
∵∠CDM=∠DBM,
∴∠BDM+∠DBM=60°,
∴∠BMD=120°,
由特殊角的三角函数值及边角关系得出∠BMD=120°,
设点O是△BMD外接圆的圆心,由定边BD及定角∠BMD=120°,作△BMD的外接圆,
连接OB,OC,OM,
则∠BOD=120°,
∵OB=OD,
∴∠OBD=∠ODB=30°,
∴点O在AD上,∠ABO=30°,在 Rt△ABO 中,AB=2,∠ABO=30°,
,
∴,
在Rt△OCD中,CD=2,,
∴OC==,
∵在△OCM中,CM+OM≥OC,
∴,
根据OM、OC的长,由三角形三边关系得出CM的最小值,
∴当O,C,M三点共线时,CM的值最小,
即CM的最小值为 .
此时点M在OC与⊙O的交点M'处,
∴,
过点M'作M′N⊥CD于点N,
∴∠CNM'=∠CDO=90°,
∴△CM′N∽△COD,
∴,
解得 ,
S△CDM'==,
∴存在点M,使得玻璃观赏栈道CM的值最小,最小值为 千米,
此时△CDM的面积为 平方千米.
同课章节目录
