浙教版数学七年级上册第5章一元一次方程 精品单元测试(含解析)
文档属性
| 名称 | 浙教版数学七年级上册第5章一元一次方程 精品单元测试(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-25 13:20:45 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
苏教版七年级上册数学 第五单元 单元测试
【浙教版】
学校:___________姓名:___________班级:___________考号:___________
满分:120分 考试时间:120分钟
题号 一 二 三 总分
得分
选择题(本大题共10小题,每小题3分,共30分。下列各题的备选答案中,只有一项是最符合题意的,请选出。)
1.下列方程中,是一元一次方程的是( )
A.=﹣1 B.x2=4x+5 C.8﹣x=1 D.x+y=7
2.若ax=ay,那么下列等式一定成立的是( )
A.x=y B.x=|y| C.(a﹣1)x=(a﹣1)y D.3﹣ax=3﹣ay
3.一元一次方程6(x﹣2)=8(x﹣2)的解为( )
A.x=1 B.x=2 C.x=3 D.x=6
4.已知关于x的方程(k2﹣4)x2+(k﹣2)x=k+6是一元一次方程,则方程的解为( )
A.﹣2 B.2 C.﹣6 D.﹣1
5.下列方程变形不正确的是( )
A.4x﹣3=3x+2变形得:4x﹣3x=2+3
B.3x=2变形得:
C.2(3x﹣2)=3(x+1)变形得:6x﹣4=3x+3
D.变形得:4x﹣1=3x+18
6.已知关于x的方程2x+a﹣9=0的解是x=﹣2,则a的值是( )
A.5 B.﹣5 C.12 D.13
7.将一堆糖果分给幼儿园的小朋友,如果每人2颗,那么就多4颗;如果每人3颗,那么就少6颗.设有糖果x颗,则可得方程为( )
A. B.2x+4=3x﹣6 C. D.
8.解方程时,小刚在去分母的过程中,右边的“﹣1”漏乘了公分母6,因而求得方程的解为x=2,则方程正确的解是( )
A.x=﹣3 B.x=﹣2 C. D.
9.若关于x的方程x=﹣无解,则a的值为( )
A.1 B.﹣1 C.0 D.±1
10.面的框图表示小明解方程3(x﹣1)=5+x的流程,其中,步骤④的依据是( )
A.等式性质1 B.等式性质2 C.去括号法则 D.乘法分配律
二、填空题(本大题共10小题,每小题4分,共40分。)
11.已知方程(k﹣2)x|k﹣1|﹣2017=2021是关于x的一元一次方程,则k= .
12.解方程5(x﹣2)=6(﹣).有以下四个步骤,其中第①步的依据是 .
解:①去括号,得5x﹣10=3x﹣2.
②移项,得5x﹣3x=10﹣2.
③合并同类项,得2x=8.
④系数化为1,得x=4.
13.代数式与代数式k+3的值相等时,k的值为 .
14.定义新运算:a b=a﹣b+ab,例如:(﹣4) 3=﹣4﹣3+(﹣4)×3=﹣19,那么当(﹣x) (﹣2)=2x时,x= .
15.若代数式5x﹣5与2x﹣9的值互为相反数,则x= .
16.王阿姨购回一批儿童鞋,加价15%后定价出售,每双46元,这种儿童鞋的进价是 元.
17.某工厂甲车间有54人,乙车间有48人,要使甲车间人数是乙车间人数的2倍,则需要从乙车间调往甲车间 人.
18.我们知道,,…
因此关于x的方程=120的解是 x= ;
当于x的方程=2021的解是 x= (用含n的式子表示).
19.整式ax+2b的值随x的取值不同而不同,如表是当x取不同值时对应的整式的值,则关于x的方程﹣ax﹣2b=2的解是 x= .
x ﹣2 ﹣1 0 1 2
ax+2b 2 0 ﹣2 ﹣4 ﹣6
20.小明解方程+1=时,由于粗心大意,在去分母时,方程左边的1没有乘以10,由此得方程的解为x=4,则a= .
三、解答题(本大题共6小题,前5小题每小题8分,第6小题10分,共50分。解答应写出文字说明、证明过程或演算步骤.)
21.解方程.
(1)12﹣2(x﹣5)=1﹣5x;
(2)﹣=1.
22.列方程求解:当k取何值时,代数式的值比的值大4?
23.我们规定一种新的运算“ ”:a b=a+ab﹣3b.例如:4 2=4+4×2﹣3×2=6,5 (﹣3)=5+5×(﹣3)﹣3×(﹣3)=﹣1.
(1)(﹣1) 3= ﹣13 ,(2x﹣1) = 3x﹣3 ;
(2)若4 (x+1)=(2x﹣1) ,求x的值.
24.在做解方程练习时,有一个方程“y﹣=y+■”题中■处不清晰,李明问老师,老师只是说:“■是一个有理数,该方程的解与当x=2时整式5(x﹣1)﹣2(x﹣2)﹣4的值相同.”依据老师的提示,请你帮李明找到“■”这个有理数,并求出方程的解.
25.两船从同一港口同时出发反向而行,甲船顺水,乙船逆水,两船在静水中的速度都是50km/h,水流速度是akm/h.
(1)2h后两船相距多远?
(2)2h后甲船比乙船多航行多少千米?
一艘小快艇送游客在甲、乙两个码头间往返,其中去程的时间是回程的时间3倍,则小快艇在静水中的速度v与水流速度a的关系是 .
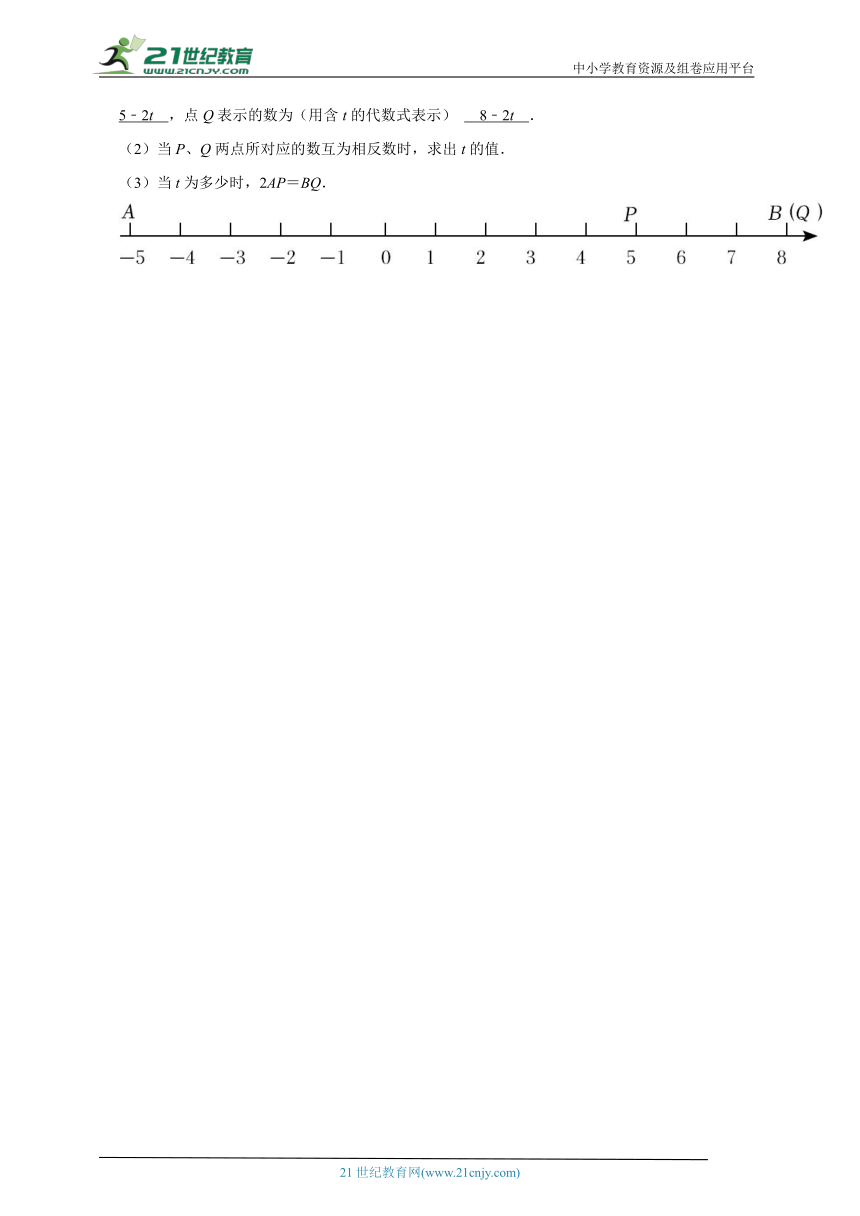
26.已知数轴上有A,B两点,点A位于原点左侧,离原点5个单位,点B位于原点右侧,离原点8个单位.已知P、Q是数轴上的两动点,点Q在点P的右侧3个单位处,当点P运动时,点Q也随之运动.出发时点Q与点B重合,点P以每秒2个单位的速度沿着B→A的路线运动,当点P到达点A时运动停止.设运动时间为t秒.
(1)点A表示的数为 ﹣5 ,点B表示的数为 8 ,点P表示的数为(用含t的代数式表示) 5﹣2t ,点Q表示的数为(用含t的代数式表示) 8﹣2t .
(2)当P、Q两点所对应的数互为相反数时,求出t的值.
(3)当t为多少时,2AP=BQ.
参考答案
选择题
1.【思路点拨】根据一元一次方程的定义:只含有一个未知数(元),并且未知数的指数是1(次)的方程叫做一元一次方程,它的一般形式是ax+b=0(a,b是常数且a≠0),对各选项分析判断后利用排除法求解.
【答案】解:A、该方程是分式方程,故本选项不符合题意.
B、该方程中的未知数最高次数是2,不是一元一次方程,故本选项不符合题意.
C、该方程符合一元一次方程的定义,故本选项符合题意.
D、该方程中含有2个未知数,不是一元一次方程,故本选项不符合题意.
故选:C.
2.【思路点拨】利用等式的性质对每个式子进行变形即可找出答案.
【答案】解:A、当a=0时,x与y不一定相等,故本选项错误;
B、当a=0时,x与|y|不一定相等,故本选项错误;
C、当a=0时,x与y不一定相等,故本选项错误;
D、等式ax=ay的两边同时乘﹣1,再同时加上3,该等式仍然成立,故本选项正确.
故选:D.
3.【思路点拨】方程去括号,移项,合并同类项,把x系数化为1,即可求出解.
【答案】解:去括号得:6x﹣12=8x﹣16,
移项得:6x﹣8x=﹣16+12,
合并得:﹣2x=﹣4,
解得:x=2.
故选:B.
4.【思路点拨】根据一元一次方程的定义得出k2﹣4=0且k﹣2≠0,求出k的值即可得到一元一次方程,解方程即可.
【答案】解:∵方程(k2﹣4)x2+(k﹣2)x=k+6是关于x的一元一次方程,
∴,
解得:k=﹣2,
所以方程为﹣4x=﹣2+6,
解得:x=﹣1,
故选:D.
5.【思路点拨】各项方程变形得到结果,即可作出判断.
【答案】解:A、4x﹣3=3x+2变形得:4x﹣3x=2+3,不符合题意;
B、3x=2变形得:x=,不符合题意;
C、2(3x﹣2)=3(x+1)变形得:6x﹣4=3x+3,不符合题意;
D、x﹣1=x+3变形得:4x﹣6=3x+18,符合题意.
故选:D.
6.【思路点拨】把x=﹣2代入方程计算即可求出a的值.
【答案】解:把x=﹣2代入方程2x+a﹣9=0得:﹣4+a﹣9=0,
解得:a=13.
故选:D.
7.【思路点拨】设有糖果x颗,根据该幼儿园小朋友的人数不变,即可得出关于x的一元一次方程,此题得解.
【答案】解:设有糖果x颗,
根据题意得:.
故选:A.
8.【思路点拨】根据“在去分母的过程中,右边的“﹣1”漏乘了公分母6,因而求得方程的解为x=2”可得x=2是方程2(2x﹣1)=3(x+a)﹣1的解,进而求出a的值,再根据求解一元一次方程的步骤进行求解即可.
【答案】解:由题意得,
x=2是方程2(2x﹣1)=3(x+a)﹣1的解,
所以a=,
则正确解为:
去分母得,2(2x﹣1)=3(x+)﹣6,
去括号得,4x﹣2=3x+1﹣6,
移项合并同类项得,x=﹣3,
故选:A.
9.【思路点拨】若一元一次方程ax+b=0无解,则a=0,b≠0,据此可得出a的值.
【答案】解:x=﹣,
去分母得,2ax=3x﹣x+6,
整理得,(2a﹣2)x﹣6=0,
∵方程无解,
∴2a﹣2=0,
解得a=1.
故选:A.
10.【思路点拨】利用等式的基本性质判断即可.
【答案】解:下面的框图表示小明解方程3(x﹣1)=5+x的流程,其中,步骤④的依据是等式性质2,
故选:B.
填空题
11.【思路点拨】根据一元一次方程的定义得出k﹣2≠0且|k﹣1|=1,再求出即可.
【答案】解:∵方程(k﹣2)x|k﹣1|﹣2017=2021是关于x的一元一次方程,
∴k﹣2≠0且|k﹣1|=1,
解得:k=0,
故答案为:0.
12.【思路点拨】解决此题应先去括号,再移项,移项时要注意符号的变化.
【答案】解:第①步去括号的依据是:乘法分配律.
故答案是:乘法分配律.
13.【思路点拨】根据题意可列出两个代数式相等时的方程,解方程即可.
【答案】解:根据题意得:=k+3,
去分母得:4(2k﹣1)=3k+36,
去括号得:8k﹣4=3k+36,
移项合并同类项得:5k=40,
解得:k=8.
故答案为:8.
14.【思路点拨】已知等式利用题中的新定义列出方程,计算即可求出解.
【答案】解:∵a b=a﹣b+ab,(﹣x) (﹣2)=2x,
∴﹣x+2+2x=2x,
解得x=2.
故答案为:2.
15.【思路点拨】首先根据题意,可得:(5x﹣5)+(2x﹣9)=0;然后去括号、移项、合并同类项、系数化为1,求出x的值即可.
【答案】解:∵代数式5x﹣5与2x﹣9的值互为相反数,
∴(5x﹣5)+(2x﹣9)=0,
去括号,可得:5x﹣5+2x﹣9=0,
移项,可得:5x+2x=5+9,
合并同类项,可得:7x=14,
系数化为1,可得:x=2.
故答案为:2.
16.【思路点拨】设进价为x元,根据进价+加价=定价列出方程求解即可.
【答案】解:设进价为x元,
由题意得x(1+15%)=46,
解得x=40,
∴这种儿童鞋的进价是40元,
故答案为:40.
17.【思路点拨】设需要从乙车间调往甲车间x人,则调动后甲车间的人数为(54+x)人,乙车间有(48﹣x)人,再根据“甲车间人数是乙车间人数的2倍”,列出方程解答即可.
【答案】解:设需要从乙车间调往甲车间x人,则调动后甲车间的人数为(54+x)人,乙车间有(48﹣x)人,根据题意得
54+x=2(48﹣x),
解得x=14.
答:需要从乙车间调往甲车间14人.
故答案为:14.
18.【思路点拨】先化简,再合并同类项,最后将x的系数化为,进而解决此题.
【答案】解:∵=120,
∴(1﹣)x+.
∴=120.
∴.
∴x=160.
∵=2021,
∴.
∴.
∴.
∴x=.
故答案为:x=160,x=
19.【思路点拨】根据图表求得一元一次方程﹣ax﹣2b=2为2x+2=2,即可得出答案.
【答案】解:∵当x=0时,ax+2b=﹣2,
∴2b=﹣2,b=﹣1,
∵x=﹣2时,ax+2b=2,
∴﹣2a﹣2=2,a=﹣2,
∴﹣ax﹣2b=2为2x+2=2,
解得x=0.
故答案为:x=0.
20.【思路点拨】由于去分母时,方程左边的1没有乘以10,所以方程2(2x﹣1)+1=5(x+a),然后把x=4代入此方程可求出a的值.
【答案】解:根据题意,x=4为方程2(2x﹣1)+1=5(x+a)的解,
所以2(8﹣1)+1=5(4+a),
解得a=﹣1.
故答案为﹣1.
解答题
21.【思路点拨】(1)方程去括号,移项合并,把x系数化为1,即可求出解;
(2)方程去分母,去括号,移项合并,把x系数化为1,即可求出解.
【答案】解:(1)去括号得:12﹣2x+10=1﹣5x,
移项得:5x﹣2x=1﹣12﹣10,
合并同类项得:3x=﹣21,
解得:x=﹣7;
(2)去分母得:x﹣7﹣2(5x+8)=4,
去括号得:x﹣7﹣10x﹣16=4,
移项得:x﹣10x=4+16+7,
合并同类项得:﹣9x=27,
解得:x=﹣3.
22.【思路点拨】根据题意列出方程,求出方程的解即可得到k的值.
【答案】解:依题意得:﹣=4,
去分母得:2k﹣2﹣9k﹣9=24,
移项合并得:﹣7k=35,
解得:k=﹣5.
23.【思路点拨】(1)两式利用题中的新定义计算即可得到结果;
(2)已知等式利用题中的新定义化简,计算即可求出x的值.
【答案】解:(1)根据题中的新定义得:
(﹣1) 3=﹣1﹣3﹣9=﹣13;(2x﹣1) =2x﹣1+(2x﹣1)﹣=3x﹣3;
故答案为:﹣13,3x﹣3;
(2)已知等式利用题中的新定义化简得:
4+4(x+1)﹣3(x+1)=3x﹣3,
去括号得:4+4x+4﹣3x﹣3=3x﹣3,
移项合并得:﹣2x=﹣8,
解得:x=4.
24.【思路点拨】利用“该方程的解与当x=2时整式5(x﹣1)﹣2(x﹣2)﹣4的值相同”求出方程的解;再将方程的解代入y﹣=y+■中求得■.
【答案】解:当x=2时,整式5(x﹣1)﹣2(x﹣2)﹣4=5×(2﹣1)﹣2×(2﹣2)﹣4=1.
∵方程的解与当x=2时整式5(x﹣1)﹣2(x﹣2)﹣4的值相同,
∴方程的解为:y=1.
当y=1时,1﹣=×1+■.
解得:■=1﹣.
答:“■”这个有理数为,方程的解为:y=1.
25.【思路点拨】(1)根据顺水速度=50+a,逆水速度=50﹣a,再根据路程=速度×时间,即可计算出2h后两船相距多远;
(2)根据顺水速度=50+a,逆水速度=50﹣a,再根据路程=速度×时间,即可计算出2h后甲船比乙船多航行多少千米;
(3)设回程用的时间为x小时,则去程用的时间为3x小时,再根据去程和回程的路程是一样的,即可列出相应的方程,从而可以求得v与a的关系.
【答案】解:(1)由题意可得,
2(50+a)+2(50﹣a)
=100+2a+100﹣2a
=200(千米),
答:2h后两船相距200千米;
(2)由题意可得,
2(50+a)﹣2(50﹣a)
=100+2a﹣100+2a
=4a(千米),
答:2h后甲船比乙船多航行4a千米;
(3)由题意可得,去程为逆水航行,回程为顺水航行,
设回程用的时间为x小时,则去程用的时间为3x小时,
3x(v﹣a)=x(v+a),
解得v=2a,
即小快艇在静水中的速度v与水流速度a的关系是v=2a,
故答案为:v=2a.
26.【思路点拨】(1)根据点A和点B的位置与它们距离原点的距离可得A、B表示的数;根据点P和点Q的运动方向和速度可得点P和点Q表示的数;
(2)由题意得,5﹣2t=﹣(8﹣2t),解方程可得答案;
(3)分别用含t的代数式表示出AP和BQ,再列方程即可.
【答案】解:(1)∵点A位于原点左侧,离原点5个单位,点B位于原点右侧,离原点8个单位,
∴点A表示的数是﹣5,点B表示的数是8,
∴点P表示的数是5﹣2t,点Q表示的数是5﹣2t+3=8﹣2t,
故答案为:﹣5,8,5﹣2t,8﹣2t;
(2)由题意得,5﹣2t=﹣(8﹣2t),
解得t=;
(3)由题意得,AP=5﹣2t﹣(﹣5)=10﹣2t,BQ=8﹣(8﹣2t)=2t,
∴2(10﹣2t)=2t,
解得t=.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
苏教版七年级上册数学 第五单元 单元测试
【浙教版】
学校:___________姓名:___________班级:___________考号:___________
满分:120分 考试时间:120分钟
题号 一 二 三 总分
得分
选择题(本大题共10小题,每小题3分,共30分。下列各题的备选答案中,只有一项是最符合题意的,请选出。)
1.下列方程中,是一元一次方程的是( )
A.=﹣1 B.x2=4x+5 C.8﹣x=1 D.x+y=7
2.若ax=ay,那么下列等式一定成立的是( )
A.x=y B.x=|y| C.(a﹣1)x=(a﹣1)y D.3﹣ax=3﹣ay
3.一元一次方程6(x﹣2)=8(x﹣2)的解为( )
A.x=1 B.x=2 C.x=3 D.x=6
4.已知关于x的方程(k2﹣4)x2+(k﹣2)x=k+6是一元一次方程,则方程的解为( )
A.﹣2 B.2 C.﹣6 D.﹣1
5.下列方程变形不正确的是( )
A.4x﹣3=3x+2变形得:4x﹣3x=2+3
B.3x=2变形得:
C.2(3x﹣2)=3(x+1)变形得:6x﹣4=3x+3
D.变形得:4x﹣1=3x+18
6.已知关于x的方程2x+a﹣9=0的解是x=﹣2,则a的值是( )
A.5 B.﹣5 C.12 D.13
7.将一堆糖果分给幼儿园的小朋友,如果每人2颗,那么就多4颗;如果每人3颗,那么就少6颗.设有糖果x颗,则可得方程为( )
A. B.2x+4=3x﹣6 C. D.
8.解方程时,小刚在去分母的过程中,右边的“﹣1”漏乘了公分母6,因而求得方程的解为x=2,则方程正确的解是( )
A.x=﹣3 B.x=﹣2 C. D.
9.若关于x的方程x=﹣无解,则a的值为( )
A.1 B.﹣1 C.0 D.±1
10.面的框图表示小明解方程3(x﹣1)=5+x的流程,其中,步骤④的依据是( )
A.等式性质1 B.等式性质2 C.去括号法则 D.乘法分配律
二、填空题(本大题共10小题,每小题4分,共40分。)
11.已知方程(k﹣2)x|k﹣1|﹣2017=2021是关于x的一元一次方程,则k= .
12.解方程5(x﹣2)=6(﹣).有以下四个步骤,其中第①步的依据是 .
解:①去括号,得5x﹣10=3x﹣2.
②移项,得5x﹣3x=10﹣2.
③合并同类项,得2x=8.
④系数化为1,得x=4.
13.代数式与代数式k+3的值相等时,k的值为 .
14.定义新运算:a b=a﹣b+ab,例如:(﹣4) 3=﹣4﹣3+(﹣4)×3=﹣19,那么当(﹣x) (﹣2)=2x时,x= .
15.若代数式5x﹣5与2x﹣9的值互为相反数,则x= .
16.王阿姨购回一批儿童鞋,加价15%后定价出售,每双46元,这种儿童鞋的进价是 元.
17.某工厂甲车间有54人,乙车间有48人,要使甲车间人数是乙车间人数的2倍,则需要从乙车间调往甲车间 人.
18.我们知道,,…
因此关于x的方程=120的解是 x= ;
当于x的方程=2021的解是 x= (用含n的式子表示).
19.整式ax+2b的值随x的取值不同而不同,如表是当x取不同值时对应的整式的值,则关于x的方程﹣ax﹣2b=2的解是 x= .
x ﹣2 ﹣1 0 1 2
ax+2b 2 0 ﹣2 ﹣4 ﹣6
20.小明解方程+1=时,由于粗心大意,在去分母时,方程左边的1没有乘以10,由此得方程的解为x=4,则a= .
三、解答题(本大题共6小题,前5小题每小题8分,第6小题10分,共50分。解答应写出文字说明、证明过程或演算步骤.)
21.解方程.
(1)12﹣2(x﹣5)=1﹣5x;
(2)﹣=1.
22.列方程求解:当k取何值时,代数式的值比的值大4?
23.我们规定一种新的运算“ ”:a b=a+ab﹣3b.例如:4 2=4+4×2﹣3×2=6,5 (﹣3)=5+5×(﹣3)﹣3×(﹣3)=﹣1.
(1)(﹣1) 3= ﹣13 ,(2x﹣1) = 3x﹣3 ;
(2)若4 (x+1)=(2x﹣1) ,求x的值.
24.在做解方程练习时,有一个方程“y﹣=y+■”题中■处不清晰,李明问老师,老师只是说:“■是一个有理数,该方程的解与当x=2时整式5(x﹣1)﹣2(x﹣2)﹣4的值相同.”依据老师的提示,请你帮李明找到“■”这个有理数,并求出方程的解.
25.两船从同一港口同时出发反向而行,甲船顺水,乙船逆水,两船在静水中的速度都是50km/h,水流速度是akm/h.
(1)2h后两船相距多远?
(2)2h后甲船比乙船多航行多少千米?
一艘小快艇送游客在甲、乙两个码头间往返,其中去程的时间是回程的时间3倍,则小快艇在静水中的速度v与水流速度a的关系是 .
26.已知数轴上有A,B两点,点A位于原点左侧,离原点5个单位,点B位于原点右侧,离原点8个单位.已知P、Q是数轴上的两动点,点Q在点P的右侧3个单位处,当点P运动时,点Q也随之运动.出发时点Q与点B重合,点P以每秒2个单位的速度沿着B→A的路线运动,当点P到达点A时运动停止.设运动时间为t秒.
(1)点A表示的数为 ﹣5 ,点B表示的数为 8 ,点P表示的数为(用含t的代数式表示) 5﹣2t ,点Q表示的数为(用含t的代数式表示) 8﹣2t .
(2)当P、Q两点所对应的数互为相反数时,求出t的值.
(3)当t为多少时,2AP=BQ.
参考答案
选择题
1.【思路点拨】根据一元一次方程的定义:只含有一个未知数(元),并且未知数的指数是1(次)的方程叫做一元一次方程,它的一般形式是ax+b=0(a,b是常数且a≠0),对各选项分析判断后利用排除法求解.
【答案】解:A、该方程是分式方程,故本选项不符合题意.
B、该方程中的未知数最高次数是2,不是一元一次方程,故本选项不符合题意.
C、该方程符合一元一次方程的定义,故本选项符合题意.
D、该方程中含有2个未知数,不是一元一次方程,故本选项不符合题意.
故选:C.
2.【思路点拨】利用等式的性质对每个式子进行变形即可找出答案.
【答案】解:A、当a=0时,x与y不一定相等,故本选项错误;
B、当a=0时,x与|y|不一定相等,故本选项错误;
C、当a=0时,x与y不一定相等,故本选项错误;
D、等式ax=ay的两边同时乘﹣1,再同时加上3,该等式仍然成立,故本选项正确.
故选:D.
3.【思路点拨】方程去括号,移项,合并同类项,把x系数化为1,即可求出解.
【答案】解:去括号得:6x﹣12=8x﹣16,
移项得:6x﹣8x=﹣16+12,
合并得:﹣2x=﹣4,
解得:x=2.
故选:B.
4.【思路点拨】根据一元一次方程的定义得出k2﹣4=0且k﹣2≠0,求出k的值即可得到一元一次方程,解方程即可.
【答案】解:∵方程(k2﹣4)x2+(k﹣2)x=k+6是关于x的一元一次方程,
∴,
解得:k=﹣2,
所以方程为﹣4x=﹣2+6,
解得:x=﹣1,
故选:D.
5.【思路点拨】各项方程变形得到结果,即可作出判断.
【答案】解:A、4x﹣3=3x+2变形得:4x﹣3x=2+3,不符合题意;
B、3x=2变形得:x=,不符合题意;
C、2(3x﹣2)=3(x+1)变形得:6x﹣4=3x+3,不符合题意;
D、x﹣1=x+3变形得:4x﹣6=3x+18,符合题意.
故选:D.
6.【思路点拨】把x=﹣2代入方程计算即可求出a的值.
【答案】解:把x=﹣2代入方程2x+a﹣9=0得:﹣4+a﹣9=0,
解得:a=13.
故选:D.
7.【思路点拨】设有糖果x颗,根据该幼儿园小朋友的人数不变,即可得出关于x的一元一次方程,此题得解.
【答案】解:设有糖果x颗,
根据题意得:.
故选:A.
8.【思路点拨】根据“在去分母的过程中,右边的“﹣1”漏乘了公分母6,因而求得方程的解为x=2”可得x=2是方程2(2x﹣1)=3(x+a)﹣1的解,进而求出a的值,再根据求解一元一次方程的步骤进行求解即可.
【答案】解:由题意得,
x=2是方程2(2x﹣1)=3(x+a)﹣1的解,
所以a=,
则正确解为:
去分母得,2(2x﹣1)=3(x+)﹣6,
去括号得,4x﹣2=3x+1﹣6,
移项合并同类项得,x=﹣3,
故选:A.
9.【思路点拨】若一元一次方程ax+b=0无解,则a=0,b≠0,据此可得出a的值.
【答案】解:x=﹣,
去分母得,2ax=3x﹣x+6,
整理得,(2a﹣2)x﹣6=0,
∵方程无解,
∴2a﹣2=0,
解得a=1.
故选:A.
10.【思路点拨】利用等式的基本性质判断即可.
【答案】解:下面的框图表示小明解方程3(x﹣1)=5+x的流程,其中,步骤④的依据是等式性质2,
故选:B.
填空题
11.【思路点拨】根据一元一次方程的定义得出k﹣2≠0且|k﹣1|=1,再求出即可.
【答案】解:∵方程(k﹣2)x|k﹣1|﹣2017=2021是关于x的一元一次方程,
∴k﹣2≠0且|k﹣1|=1,
解得:k=0,
故答案为:0.
12.【思路点拨】解决此题应先去括号,再移项,移项时要注意符号的变化.
【答案】解:第①步去括号的依据是:乘法分配律.
故答案是:乘法分配律.
13.【思路点拨】根据题意可列出两个代数式相等时的方程,解方程即可.
【答案】解:根据题意得:=k+3,
去分母得:4(2k﹣1)=3k+36,
去括号得:8k﹣4=3k+36,
移项合并同类项得:5k=40,
解得:k=8.
故答案为:8.
14.【思路点拨】已知等式利用题中的新定义列出方程,计算即可求出解.
【答案】解:∵a b=a﹣b+ab,(﹣x) (﹣2)=2x,
∴﹣x+2+2x=2x,
解得x=2.
故答案为:2.
15.【思路点拨】首先根据题意,可得:(5x﹣5)+(2x﹣9)=0;然后去括号、移项、合并同类项、系数化为1,求出x的值即可.
【答案】解:∵代数式5x﹣5与2x﹣9的值互为相反数,
∴(5x﹣5)+(2x﹣9)=0,
去括号,可得:5x﹣5+2x﹣9=0,
移项,可得:5x+2x=5+9,
合并同类项,可得:7x=14,
系数化为1,可得:x=2.
故答案为:2.
16.【思路点拨】设进价为x元,根据进价+加价=定价列出方程求解即可.
【答案】解:设进价为x元,
由题意得x(1+15%)=46,
解得x=40,
∴这种儿童鞋的进价是40元,
故答案为:40.
17.【思路点拨】设需要从乙车间调往甲车间x人,则调动后甲车间的人数为(54+x)人,乙车间有(48﹣x)人,再根据“甲车间人数是乙车间人数的2倍”,列出方程解答即可.
【答案】解:设需要从乙车间调往甲车间x人,则调动后甲车间的人数为(54+x)人,乙车间有(48﹣x)人,根据题意得
54+x=2(48﹣x),
解得x=14.
答:需要从乙车间调往甲车间14人.
故答案为:14.
18.【思路点拨】先化简,再合并同类项,最后将x的系数化为,进而解决此题.
【答案】解:∵=120,
∴(1﹣)x+.
∴=120.
∴.
∴x=160.
∵=2021,
∴.
∴.
∴.
∴x=.
故答案为:x=160,x=
19.【思路点拨】根据图表求得一元一次方程﹣ax﹣2b=2为2x+2=2,即可得出答案.
【答案】解:∵当x=0时,ax+2b=﹣2,
∴2b=﹣2,b=﹣1,
∵x=﹣2时,ax+2b=2,
∴﹣2a﹣2=2,a=﹣2,
∴﹣ax﹣2b=2为2x+2=2,
解得x=0.
故答案为:x=0.
20.【思路点拨】由于去分母时,方程左边的1没有乘以10,所以方程2(2x﹣1)+1=5(x+a),然后把x=4代入此方程可求出a的值.
【答案】解:根据题意,x=4为方程2(2x﹣1)+1=5(x+a)的解,
所以2(8﹣1)+1=5(4+a),
解得a=﹣1.
故答案为﹣1.
解答题
21.【思路点拨】(1)方程去括号,移项合并,把x系数化为1,即可求出解;
(2)方程去分母,去括号,移项合并,把x系数化为1,即可求出解.
【答案】解:(1)去括号得:12﹣2x+10=1﹣5x,
移项得:5x﹣2x=1﹣12﹣10,
合并同类项得:3x=﹣21,
解得:x=﹣7;
(2)去分母得:x﹣7﹣2(5x+8)=4,
去括号得:x﹣7﹣10x﹣16=4,
移项得:x﹣10x=4+16+7,
合并同类项得:﹣9x=27,
解得:x=﹣3.
22.【思路点拨】根据题意列出方程,求出方程的解即可得到k的值.
【答案】解:依题意得:﹣=4,
去分母得:2k﹣2﹣9k﹣9=24,
移项合并得:﹣7k=35,
解得:k=﹣5.
23.【思路点拨】(1)两式利用题中的新定义计算即可得到结果;
(2)已知等式利用题中的新定义化简,计算即可求出x的值.
【答案】解:(1)根据题中的新定义得:
(﹣1) 3=﹣1﹣3﹣9=﹣13;(2x﹣1) =2x﹣1+(2x﹣1)﹣=3x﹣3;
故答案为:﹣13,3x﹣3;
(2)已知等式利用题中的新定义化简得:
4+4(x+1)﹣3(x+1)=3x﹣3,
去括号得:4+4x+4﹣3x﹣3=3x﹣3,
移项合并得:﹣2x=﹣8,
解得:x=4.
24.【思路点拨】利用“该方程的解与当x=2时整式5(x﹣1)﹣2(x﹣2)﹣4的值相同”求出方程的解;再将方程的解代入y﹣=y+■中求得■.
【答案】解:当x=2时,整式5(x﹣1)﹣2(x﹣2)﹣4=5×(2﹣1)﹣2×(2﹣2)﹣4=1.
∵方程的解与当x=2时整式5(x﹣1)﹣2(x﹣2)﹣4的值相同,
∴方程的解为:y=1.
当y=1时,1﹣=×1+■.
解得:■=1﹣.
答:“■”这个有理数为,方程的解为:y=1.
25.【思路点拨】(1)根据顺水速度=50+a,逆水速度=50﹣a,再根据路程=速度×时间,即可计算出2h后两船相距多远;
(2)根据顺水速度=50+a,逆水速度=50﹣a,再根据路程=速度×时间,即可计算出2h后甲船比乙船多航行多少千米;
(3)设回程用的时间为x小时,则去程用的时间为3x小时,再根据去程和回程的路程是一样的,即可列出相应的方程,从而可以求得v与a的关系.
【答案】解:(1)由题意可得,
2(50+a)+2(50﹣a)
=100+2a+100﹣2a
=200(千米),
答:2h后两船相距200千米;
(2)由题意可得,
2(50+a)﹣2(50﹣a)
=100+2a﹣100+2a
=4a(千米),
答:2h后甲船比乙船多航行4a千米;
(3)由题意可得,去程为逆水航行,回程为顺水航行,
设回程用的时间为x小时,则去程用的时间为3x小时,
3x(v﹣a)=x(v+a),
解得v=2a,
即小快艇在静水中的速度v与水流速度a的关系是v=2a,
故答案为:v=2a.
26.【思路点拨】(1)根据点A和点B的位置与它们距离原点的距离可得A、B表示的数;根据点P和点Q的运动方向和速度可得点P和点Q表示的数;
(2)由题意得,5﹣2t=﹣(8﹣2t),解方程可得答案;
(3)分别用含t的代数式表示出AP和BQ,再列方程即可.
【答案】解:(1)∵点A位于原点左侧,离原点5个单位,点B位于原点右侧,离原点8个单位,
∴点A表示的数是﹣5,点B表示的数是8,
∴点P表示的数是5﹣2t,点Q表示的数是5﹣2t+3=8﹣2t,
故答案为:﹣5,8,5﹣2t,8﹣2t;
(2)由题意得,5﹣2t=﹣(8﹣2t),
解得t=;
(3)由题意得,AP=5﹣2t﹣(﹣5)=10﹣2t,BQ=8﹣(8﹣2t)=2t,
∴2(10﹣2t)=2t,
解得t=.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
