浙教版数学七年级上册第4章代数式 精品单元测试(含解析)
文档属性
| 名称 | 浙教版数学七年级上册第4章代数式 精品单元测试(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-25 13:25:37 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
苏教版七年级上册数学 第一单元 单元测试
【浙教版】
学校:___________姓名:___________班级:___________考号:___________
满分:120分 考试时间:120分钟
题号 一 二 三 总分
得分
选择题(本大题共10小题,每小题3分,共30分。下列各题的备选答案中,只有一项是最符合题意的,请选出。)
1.计算(﹣m)3+(﹣m)3的结果是( )
A.2m3 B.﹣2m3 C.﹣m6 D.m6
2.列式子正确的是( )
A.x﹣(y﹣z)=x﹣y﹣z B.x+2y﹣2z=x﹣2(y+z)
C.﹣(x﹣y+z)=﹣x﹣y﹣z D.﹣2(x+y)﹣z=﹣2x﹣2y﹣z
3.已知单项式﹣3am﹣1b6与ab2n是同类项,则m+n的值是( )
A.0 B.3 C.4 D.5
4.下列概念表述正确的是( )
A.单项式ab的系数是0,次数是2
B.﹣4a2b,3ab,5是多项式﹣4a2b+3ab﹣5的项
C.单项式﹣23a3b3的系数是﹣2,次数是5
D.是二次二项式
5.下列去括号或添括号中:①2a﹣2(﹣3x+2y﹣1)=2a+6x﹣4y+2;②﹣3a3﹣[﹣2a2+(3﹣a)]=﹣3a3+2a2+a+3
;③﹣2x2+y﹣z﹣5=﹣(2x2﹣5)﹣(z﹣y);④3a2﹣6a﹣4ab+1=3a2﹣[6a+(4ab﹣1)],其中正确的序号是( )
A.①② B.②③ C.①④ D.③④
6.已知单项式2a6bn+1与a3mb3的和仍然是单项式,则式子9m2﹣mn﹣36的值为( )
A.﹣1 B.﹣2 C.﹣3 D.﹣4
7.如果代数式2x+3y+1的值为4,那么代数式3﹣4x﹣6y的值为( )
A.1 B.﹣5 C.3 D.﹣3
8.如果(k﹣2)x3+(|k|﹣2)x2﹣6是关于字母x的三次二项式,则k的值为( )
A.±2 B.﹣2 C.2 D.0
9.当x=3时,代数式px3+qx﹣1的值为4,则当x=﹣3时,px3+qx﹣1的值是( )
A.﹣4 B.﹣6 C.4 D.6
10.若多项式4x2﹣3x+7与多项式5x3+(m﹣2)x2﹣2x+3相加后,结果不含x2项,则常数m的值是( )
A.﹣2 B.2 C.5 D.6
二、填空题(本大题共10小题,每小题4分,共40分。)
11.“a的3倍与b的平方的差”用代数式表示为 .
12.多项式2a3b+3b﹣1是 次 项式,其中常数项为 .
13.设单项式﹣x3y2z的系数为α,次数是b,则α+b= .
14.若x2+x﹣3=0,则代数式2(x﹣2)(x+2)﹣x(x﹣1)的值是 .
15.多项式a2b+2ab4﹣38是 次 项式.
16.代数式﹣2a3bm与4an+1b4是同类项,则m+n= .
17.某种商品每件标价a元,若以标价的七折销售,则这种商品每件的售价为 元 .
18.有理数a,b,c在数轴上的位置如图所示,则|a+c|﹣|a﹣b|+|b﹣c|= .
19.若代数式(2x2+ax﹣y+6)﹣(2bx2﹣3x﹣5y﹣1)的值与字母x的取值无关,则代数式a2b的值为 .
20.下面是小强做的一道多项式的加减运算题,由于他不小心把一滴墨水滴在了上面:(﹣x2+3xy﹣y2)﹣2(﹣x2+4xy﹣y2)=﹣5xy+y2,阴影部分即为被墨迹弄污的部分.那么被墨汁遮住的一项应是 .
21.观察下列单项式的排列规律:3x,﹣7x2,11x3,﹣15x4,19x5,…,照这样排列第n个单项式应是 .
三、解答题(本大题共6小题,前5小题每小题8分,第6小题10分,共50分。解答应写出文字说明、证明过程或演算步骤.)
21.代数式:①﹣x;②x2+x﹣1;③;④;⑤;⑥πm3y;⑦;⑧.
(1)请上述代数式的序号分别填在相应的圆圈内:
(2)其中次数最高的多项式是 次项式;
(3)其中次数最高的单项式的次数是 ,系数是 .
22.化简:
(1)2(2a2+9b)+3(﹣5a2﹣4b) (2)3x2﹣2[7x﹣(4x﹣3)﹣2x2]
(3)(5ab+3a2)﹣2(a2+2ab); (4)8x2﹣[﹣3x﹣2(x2﹣7x﹣5)+3]+4x.
23.在化简(2x2﹣1+3x)﹣4(x﹣x2+1)时,甲、乙两同学的解答如下:
甲:(2x2﹣1+3x)﹣4(x﹣x2+1)
=2x2﹣1+3x﹣4x﹣4x2﹣4
=(2﹣4)x2+(3﹣4)x+(﹣1﹣4)
=﹣2x2﹣x﹣5
乙:(2x2﹣1+3x)﹣4(x﹣x2+1)
=2x2﹣1+3x﹣4x+x2﹣1
=3x2﹣x﹣2
他们的解答正确吗?如不正确,
(1)把出错部分标出来,并写出正确的结果;
(2)写出正确的解题过程.
24.小云准备完成题目:化简:(□x2+6x+8)﹣(6x+5x2+2).发现系数“□”印刷不清楚.不过却知道该题标准答案的结果是常数.你能通过计算告知小云原题中“□”是几?
25.老师写出一个整式(ax2+bx﹣1)﹣(4x2+3x)(其中a,b为常数,且表示为系数),然后让同学给a,b赋予不同的数值进行计算.
(1)甲同学给出了a=5,b=﹣1,请按照甲同学给出的数值化简整式;
(2)乙同学给出一组数,计算的最后结果与x的取值无关,求a,b的值.
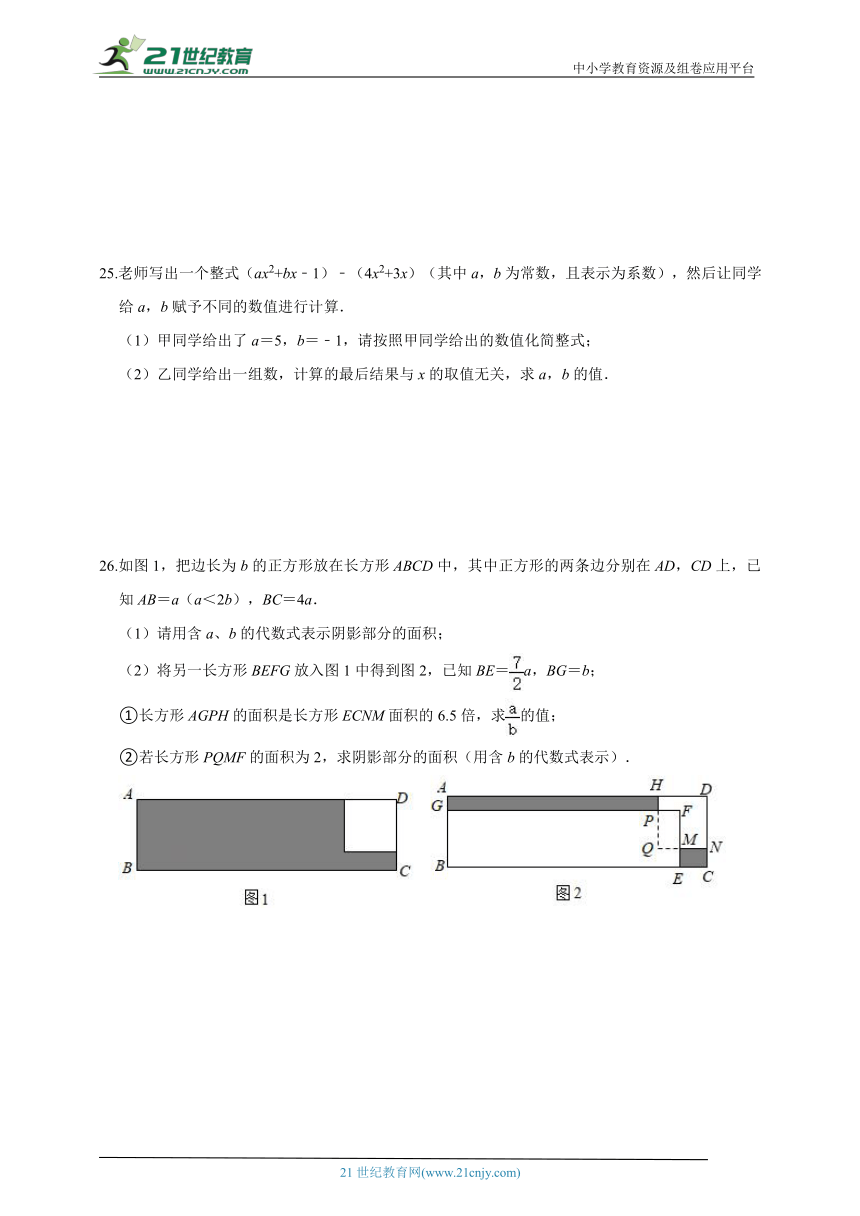
26.如图1,把边长为b的正方形放在长方形ABCD中,其中正方形的两条边分别在AD,CD上,已知AB=a(a<2b),BC=4a.
(1)请用含a、b的代数式表示阴影部分的面积;
(2)将另一长方形BEFG放入图1中得到图2,已知BE=a,BG=b;
①长方形AGPH的面积是长方形ECNM面积的6.5倍,求的值;
②若长方形PQMF的面积为2,求阴影部分的面积(用含b的代数式表示).
参考答案
选择题
1.【思路点拨】根据合并同类项法则解答即可.
【答案】解:(﹣m)3+(﹣m)3=2(﹣m)3=﹣2m3.
故选:B.
2.【思路点拨】原式各项利用去括号法则及添括号法则判断即可.
【答案】解:A、原式=x﹣y+z,不符合题意;
B、原式=x﹣2(﹣y+z),不符合题意;
C、﹣(x﹣y+z)=﹣x+y﹣z,不符合题意;
D、﹣2(x+y)﹣z=﹣2z﹣2y﹣z,符合题意;
故选:D.
3.【思路点拨】根据同类项是字母相同,且相同的字母的指数也相同,可得m、n的值,再代入所求式子计算即可.
【答案】解:∵单项式﹣3am﹣1b6与ab2n是同类项,
∴m﹣1=1,2n=6,
解得m=2,n=3,
∴m+n=2+3=5.
故选:D.
4.【思路点拨】根据单项式的系数与次数的定义、多项式的次数及其定义解决此题.
【答案】解:A.根据单项式的系数与次数的定义,单项式ab的系数是1,次数是2,故A不正确,那么A不符合题意.
B.根据多项式的定义,多项式﹣4a2b+3ab﹣5的项包括﹣4a2b、3ab、﹣5,故B不正确,那么B不符合题意.
C.根据单项式的系数与次数的定义,单项式﹣23a3b3的系数是﹣23=﹣8,次数是6,故C不正确,那么C不符合题意.
D.根据多项式的定义,是二次二项式,故D正确,那么D符合题意.
故选:D.
5.【思路点拨】根据去括号、添括号法则及合并同类项法则逐项判断即可.
【答案】解:①2a﹣2(﹣3x+2y﹣1)=2a+6x﹣4y+2,故①正确;
②﹣3a3﹣[﹣2a2+(3﹣a)]=﹣3a3﹣(﹣2a2+3﹣a)=﹣3a3+2a2﹣3+a=﹣3a3+2a2+a﹣3,故②不正确;
③﹣2x2+y﹣z﹣5=﹣(2x2+5)﹣(z﹣y),故③不正确;
④3a2﹣6a﹣4ab+1=3a2﹣[6a+(4ab﹣1)],故④正确;
故选:C.
6.【思路点拨】根据合并同类项法则得出3m=6,n+1=3,求出m、n的值,再代入求出答案即可.
【答案】解:根据题意,得3m=6,n+1=3,
解得m=2,n=2.
所以9m2﹣mn﹣36=9×22﹣2×2﹣36=﹣4.
故选:D.
7.【思路点拨】将所求的代数式适当变形,利用整体代入的思想解答即可.
【答案】解:原式=3﹣4x﹣6y
=3﹣2(2x+3y).
∵2x+3y+1=4,
∴2x+3y=3
∴原式=3﹣2×3=﹣3.
故选:D.
8.【思路点拨】根据多项式及其次数的定义、绝对值解决此题.
【答案】解:由题意得:k﹣2≠0且|k|﹣2=0.
∴k≠2且k=±2.
∴k=﹣2.
故选:B.
9.【思路点拨】将x=3代入代数式中,得到关于p,q的式子,再将x=﹣3代入代数式并整理,利用整体代入的方法解答即可得出结论.
【答案】解:∵当x=3时,代数式px3+qx﹣1的值为4,
∴27p+3q﹣1=4,
∴27p+3q=5.
∴当x=﹣3时,
px3+qx﹣1
=﹣27p﹣3p﹣1
=﹣(27p+3q)﹣1
=﹣5﹣1
=﹣6.
故选:B.
10.【思路点拨】先将两式相加,合并同类项,再令x2项的系数为0,即可解除m.
【答案】解:∵4x2﹣3x+7+5x3+(m﹣2)x2﹣2x+3=5x3+(m+2)x2﹣5x+10,
而4x2﹣3x+7与多项式5x3+(m﹣2)x2﹣2x+3相加后,结果不含x2项,
∴m+2=0,
∴m=﹣2,
故选:A.
选题题
11.【思路点拨】a的3倍即为3a,b的平方即为b2,再将两者作差即可得.
【答案】解:“a的3倍与b的平方的差”用代数式表示为3a﹣b2,
故答案为:3a﹣b2.
【点睛】本题主要考查列代数式,列代数式应该注意的四个问题
1.在同一个式子或具体问题中,每一个字母只能代表一个量.
2.要注意书写的规范性.用字母表示数以后,在含有字母与数字的乘法中,通常将“×”简写作“ ”或者省略不写.
3.在数和表示数的字母乘积中,一般把数写在字母的前面,这个数若是带分数要把它化成假分数.
4.含有字母的除法,一般不用“÷”(除号),而是写成分数的形式.
12.【思路点拨】根据几个单项式的和叫做多项式,每个单项式叫做多项式的项,其中不含字母的项叫做常数项.多项式中次数最高的项的次数叫做多项式的次数,如果一个多项式含有a个单项式,次数是b,那么这个多项式就叫b次a项式可得答案.
【答案】解:多项式2a3b+3b﹣l是四次三项式,其中常数项为﹣1,
故答案为:四;三;﹣1.
13.【思路点拨】根据单项式的系数与次数的定义解决此题.
【答案】解:∵单项式﹣x3y2z的系数为﹣1,次数为6,
∴α=﹣1,b=6.
∴α+b=﹣1+6=5.
故答案为:5.
14.【思路点拨】根据多项式的项及次数的概念进行分析解答.
【答案】解:多项式a2b+2ab4﹣38含有a2b、2ab4、﹣38三项,其中2ab4的次数最高为五次,
∴多项式a2b+2ab4﹣38是五次三项式,
故答案为:五、三.
15.【思路点拨】根据同类项的定义(所含字母相同,相同字母的指数相同)即可解答.
【答案】解:∵代数式﹣2a3bm与4an+1b4是同类项,
∴n+1=3,m=4,
解得m=4,n=2,
∴m+n=4+2=6.
故答案为:6.
16.【思路点拨】根据售价=标价×0.7列式即可.
【答案】解:根据题意得,这种商品每件的售价为0.7a元.
故答案为:0.7a元.
17.【思路点拨】根据数轴可确定a、b、c的符号与绝对值的大小,从而可以去掉绝对值符号进行化简.
【答案】解:由题意得,
c<a<0<b,且|c|>|a|>|b|,
∴a+c<0,a﹣b<0,b﹣c>0,
∴|a+c|﹣|a﹣b|+|b﹣c|
=﹣(a+c)﹣[﹣(a﹣b)]+b﹣c
=﹣a﹣c+a﹣b+b﹣c
=﹣2c,
故答案为:﹣2c.
18.【思路点拨】直接利用整式的加减运算法则化简,进而得出a,b的值,进而得出答案.
【答案】解:∵代数式(2x2+ax﹣y+6)﹣(2bx2﹣3x﹣5y﹣1)的值与字母x的取值无关,
∴(2x2+ax﹣y+6)﹣(2bx2﹣3x﹣5y﹣1)
=2x2+ax﹣y+6﹣2bx2+3x+5y+1
=(2﹣2b)x2+(a+3)x+4y+7,
∴2﹣2b=0,a+3=0,
解得:b=1,a=﹣3,
∴a2b=(﹣3)2=9.
故答案为:9.
19.思路点拨】直接去括号,再合并同类项得出答案.
【答案】解:∵(﹣x2+3xy﹣y2)﹣2(﹣x2+4xy﹣y2)=﹣5xy+y2,
∴﹣x2+3xy﹣y2+5x2﹣8xy+3y2=﹣5xy+y2,
4x2﹣5xy+y2=﹣5xy+y2,
故被墨汁遮住的一项应是4x2.
故答案为:4x2.
20.【思路点拨】根据每个单项式的系数的符号,系数的绝对值以及x的次数与它排列的位数的关系即可得出结论.
【答案】解:∵观察多项式的排列发现如下规律:①奇数项为正,偶数项为负;②系数的绝对值从3开始依次相差4;③x的次数与它所在位置数相同,及第n个多项式中x的次数为n,
∴这样排列第n个单项式应是:(﹣1)n+1(4n﹣1)xn.
故答案为:(﹣1)n+1(4n﹣1)xn.
解答题
21.【思路点拨】(1)直接利用多项式以及单项式定义分析即可;
(2)直接利用多项式的次数确定方法分析得出答案;
(3)直接利用单项式的次数与系数确定方法分析即可.
【答案】解:(1)多项式:②④⑧;单项式:①⑤⑥;
(2)次数最高的多项式是二;
故答案为:二;
(3)次数最高的单项式的次数是4,系数是π.
故答案为:4,π.
22.【思路点拨】(1)首先去括号,再合并同类项即可.
(2)首先去小括号,再去中括号,再合并同类项即可.
(3)原式去括号合并即可得到结果;
(4)原式去括号合并即可得到结果.
【答案】解:(1)原式=4a2+18b﹣15a2﹣12b,
=﹣11a2+6b;
(2)原式=3x2﹣2(7x﹣4x+3﹣2x2),
=3x2﹣14x+8x﹣6+4x2,
=7x2﹣6x﹣6.
(3)原式=5ab+3a2﹣2a2﹣4ab=a2+ab;
(4)原式=8x2+3x+2x2﹣14x﹣10﹣3+4x=10x2﹣7x﹣13.
23.【思路点拨】(1)直接利用去括号法则判断得出错误原因;
(2)直接去括号,进而合并同类项得出答案.
【答案】解:(1)甲:(2x2﹣1+3x)﹣4(x﹣x2+1)
=2x2﹣1+3x﹣4x﹣4
=2x2﹣1+3x﹣4x+4x2﹣4;
乙:(2x2﹣1+3x)﹣4(x﹣x2+1)
=2x2﹣1+3x﹣4x+
=2x2﹣1+3x﹣4x+4x2﹣4;
(2)(2x2﹣1+3x)﹣4(x﹣x2+1)
=2x2﹣1+3x﹣4x+4x2﹣4
=6x2﹣x﹣5.
24.【思路点拨】根据整式的加减运算法则,先去括号,再计算加减,从而解决此题.
【答案】解:(□x2+6x+8)﹣(6x+5x2+2)
=□x2+6x+8﹣6x﹣5x2﹣2
=(□﹣5)x2+6.
∵该题标准答案的结果是常数,
∴□﹣5=0.
∴□=5.
25.【思路点拨】(1)将a=5,b=﹣1代入,再去括号、合并同类型即可得答案;
(2)先去括号、合并同类项,再根据计算的最后结果与x的取值无关列出关于a、b的方程,即可解得答案.
【答案】解:(1)∵a=5,b=﹣1,
∴(ax2+bx﹣1)﹣(4x2+3x)
=(5x2﹣x﹣1)﹣(4x2+3x)
=5x2﹣x﹣1﹣4x2﹣3x
=x2﹣4x﹣1;
(2)(ax2+bx﹣1)﹣(4x2+3x)
=ax2+bx﹣1﹣4x2﹣3x
=(a﹣4)x2+(b﹣3)x﹣1,
∵计算的最后结果与x的取值无关,
∴a﹣4=0,b﹣3=0,
∴a=4,b=3.
26.【思路点拨】(1)根据阴影部分的面积等于长方形ABCD的面积﹣边长为b的正方形面积即可得出结论;
(2)①根据长方形AGPH的面积是长方形ECNM面积的6.5倍列等式,可得答案;
②根据长方形PQMF的面积为2,列等式可得(a﹣2b)2=4,根据a<2b,得a﹣2b=﹣2,最后根据面积和可得答案.
【答案】解:(1)阴影部分的面积=a 4a﹣b2=4a2﹣b2;
(2)①∵AB=a,BG=b,
∴AG=a﹣b,
∵AD=BC=4a,DH=b,
∴AH=4a﹣b,
∵BE=a,BC=4a,
∴CE=4a﹣a=a,
∵长方形AGPH的面积是长方形ECNM面积的6.5倍,
∴(a﹣b)(4a﹣b)=6.5×a×(a﹣b),
∴3a=4b,
∴=;
②如图2,PQ=EF﹣EM=b﹣(a﹣b)=2b﹣a,
QM=QN﹣MN=b﹣a,
∵长方形PQMF的面积为2,
∴(2b﹣a)(b﹣a)=2,
(a﹣2b)2=4,
∴a﹣2b=±2,
∵a<2b,
∴a﹣2b<0,
∴a﹣2b=﹣2,
∴a=2b﹣2,
∴如图2中阴影部分的面积=长方形AGPH的面积+长方形ECNM的面积
=(a﹣b)(4a﹣b)+
=(a﹣b)(4a﹣b+a)
=(2b﹣2﹣b)(9b﹣9﹣b)
=(b﹣2)(8b﹣9)
=8b2﹣25b+18.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
苏教版七年级上册数学 第一单元 单元测试
【浙教版】
学校:___________姓名:___________班级:___________考号:___________
满分:120分 考试时间:120分钟
题号 一 二 三 总分
得分
选择题(本大题共10小题,每小题3分,共30分。下列各题的备选答案中,只有一项是最符合题意的,请选出。)
1.计算(﹣m)3+(﹣m)3的结果是( )
A.2m3 B.﹣2m3 C.﹣m6 D.m6
2.列式子正确的是( )
A.x﹣(y﹣z)=x﹣y﹣z B.x+2y﹣2z=x﹣2(y+z)
C.﹣(x﹣y+z)=﹣x﹣y﹣z D.﹣2(x+y)﹣z=﹣2x﹣2y﹣z
3.已知单项式﹣3am﹣1b6与ab2n是同类项,则m+n的值是( )
A.0 B.3 C.4 D.5
4.下列概念表述正确的是( )
A.单项式ab的系数是0,次数是2
B.﹣4a2b,3ab,5是多项式﹣4a2b+3ab﹣5的项
C.单项式﹣23a3b3的系数是﹣2,次数是5
D.是二次二项式
5.下列去括号或添括号中:①2a﹣2(﹣3x+2y﹣1)=2a+6x﹣4y+2;②﹣3a3﹣[﹣2a2+(3﹣a)]=﹣3a3+2a2+a+3
;③﹣2x2+y﹣z﹣5=﹣(2x2﹣5)﹣(z﹣y);④3a2﹣6a﹣4ab+1=3a2﹣[6a+(4ab﹣1)],其中正确的序号是( )
A.①② B.②③ C.①④ D.③④
6.已知单项式2a6bn+1与a3mb3的和仍然是单项式,则式子9m2﹣mn﹣36的值为( )
A.﹣1 B.﹣2 C.﹣3 D.﹣4
7.如果代数式2x+3y+1的值为4,那么代数式3﹣4x﹣6y的值为( )
A.1 B.﹣5 C.3 D.﹣3
8.如果(k﹣2)x3+(|k|﹣2)x2﹣6是关于字母x的三次二项式,则k的值为( )
A.±2 B.﹣2 C.2 D.0
9.当x=3时,代数式px3+qx﹣1的值为4,则当x=﹣3时,px3+qx﹣1的值是( )
A.﹣4 B.﹣6 C.4 D.6
10.若多项式4x2﹣3x+7与多项式5x3+(m﹣2)x2﹣2x+3相加后,结果不含x2项,则常数m的值是( )
A.﹣2 B.2 C.5 D.6
二、填空题(本大题共10小题,每小题4分,共40分。)
11.“a的3倍与b的平方的差”用代数式表示为 .
12.多项式2a3b+3b﹣1是 次 项式,其中常数项为 .
13.设单项式﹣x3y2z的系数为α,次数是b,则α+b= .
14.若x2+x﹣3=0,则代数式2(x﹣2)(x+2)﹣x(x﹣1)的值是 .
15.多项式a2b+2ab4﹣38是 次 项式.
16.代数式﹣2a3bm与4an+1b4是同类项,则m+n= .
17.某种商品每件标价a元,若以标价的七折销售,则这种商品每件的售价为 元 .
18.有理数a,b,c在数轴上的位置如图所示,则|a+c|﹣|a﹣b|+|b﹣c|= .
19.若代数式(2x2+ax﹣y+6)﹣(2bx2﹣3x﹣5y﹣1)的值与字母x的取值无关,则代数式a2b的值为 .
20.下面是小强做的一道多项式的加减运算题,由于他不小心把一滴墨水滴在了上面:(﹣x2+3xy﹣y2)﹣2(﹣x2+4xy﹣y2)=﹣5xy+y2,阴影部分即为被墨迹弄污的部分.那么被墨汁遮住的一项应是 .
21.观察下列单项式的排列规律:3x,﹣7x2,11x3,﹣15x4,19x5,…,照这样排列第n个单项式应是 .
三、解答题(本大题共6小题,前5小题每小题8分,第6小题10分,共50分。解答应写出文字说明、证明过程或演算步骤.)
21.代数式:①﹣x;②x2+x﹣1;③;④;⑤;⑥πm3y;⑦;⑧.
(1)请上述代数式的序号分别填在相应的圆圈内:
(2)其中次数最高的多项式是 次项式;
(3)其中次数最高的单项式的次数是 ,系数是 .
22.化简:
(1)2(2a2+9b)+3(﹣5a2﹣4b) (2)3x2﹣2[7x﹣(4x﹣3)﹣2x2]
(3)(5ab+3a2)﹣2(a2+2ab); (4)8x2﹣[﹣3x﹣2(x2﹣7x﹣5)+3]+4x.
23.在化简(2x2﹣1+3x)﹣4(x﹣x2+1)时,甲、乙两同学的解答如下:
甲:(2x2﹣1+3x)﹣4(x﹣x2+1)
=2x2﹣1+3x﹣4x﹣4x2﹣4
=(2﹣4)x2+(3﹣4)x+(﹣1﹣4)
=﹣2x2﹣x﹣5
乙:(2x2﹣1+3x)﹣4(x﹣x2+1)
=2x2﹣1+3x﹣4x+x2﹣1
=3x2﹣x﹣2
他们的解答正确吗?如不正确,
(1)把出错部分标出来,并写出正确的结果;
(2)写出正确的解题过程.
24.小云准备完成题目:化简:(□x2+6x+8)﹣(6x+5x2+2).发现系数“□”印刷不清楚.不过却知道该题标准答案的结果是常数.你能通过计算告知小云原题中“□”是几?
25.老师写出一个整式(ax2+bx﹣1)﹣(4x2+3x)(其中a,b为常数,且表示为系数),然后让同学给a,b赋予不同的数值进行计算.
(1)甲同学给出了a=5,b=﹣1,请按照甲同学给出的数值化简整式;
(2)乙同学给出一组数,计算的最后结果与x的取值无关,求a,b的值.
26.如图1,把边长为b的正方形放在长方形ABCD中,其中正方形的两条边分别在AD,CD上,已知AB=a(a<2b),BC=4a.
(1)请用含a、b的代数式表示阴影部分的面积;
(2)将另一长方形BEFG放入图1中得到图2,已知BE=a,BG=b;
①长方形AGPH的面积是长方形ECNM面积的6.5倍,求的值;
②若长方形PQMF的面积为2,求阴影部分的面积(用含b的代数式表示).
参考答案
选择题
1.【思路点拨】根据合并同类项法则解答即可.
【答案】解:(﹣m)3+(﹣m)3=2(﹣m)3=﹣2m3.
故选:B.
2.【思路点拨】原式各项利用去括号法则及添括号法则判断即可.
【答案】解:A、原式=x﹣y+z,不符合题意;
B、原式=x﹣2(﹣y+z),不符合题意;
C、﹣(x﹣y+z)=﹣x+y﹣z,不符合题意;
D、﹣2(x+y)﹣z=﹣2z﹣2y﹣z,符合题意;
故选:D.
3.【思路点拨】根据同类项是字母相同,且相同的字母的指数也相同,可得m、n的值,再代入所求式子计算即可.
【答案】解:∵单项式﹣3am﹣1b6与ab2n是同类项,
∴m﹣1=1,2n=6,
解得m=2,n=3,
∴m+n=2+3=5.
故选:D.
4.【思路点拨】根据单项式的系数与次数的定义、多项式的次数及其定义解决此题.
【答案】解:A.根据单项式的系数与次数的定义,单项式ab的系数是1,次数是2,故A不正确,那么A不符合题意.
B.根据多项式的定义,多项式﹣4a2b+3ab﹣5的项包括﹣4a2b、3ab、﹣5,故B不正确,那么B不符合题意.
C.根据单项式的系数与次数的定义,单项式﹣23a3b3的系数是﹣23=﹣8,次数是6,故C不正确,那么C不符合题意.
D.根据多项式的定义,是二次二项式,故D正确,那么D符合题意.
故选:D.
5.【思路点拨】根据去括号、添括号法则及合并同类项法则逐项判断即可.
【答案】解:①2a﹣2(﹣3x+2y﹣1)=2a+6x﹣4y+2,故①正确;
②﹣3a3﹣[﹣2a2+(3﹣a)]=﹣3a3﹣(﹣2a2+3﹣a)=﹣3a3+2a2﹣3+a=﹣3a3+2a2+a﹣3,故②不正确;
③﹣2x2+y﹣z﹣5=﹣(2x2+5)﹣(z﹣y),故③不正确;
④3a2﹣6a﹣4ab+1=3a2﹣[6a+(4ab﹣1)],故④正确;
故选:C.
6.【思路点拨】根据合并同类项法则得出3m=6,n+1=3,求出m、n的值,再代入求出答案即可.
【答案】解:根据题意,得3m=6,n+1=3,
解得m=2,n=2.
所以9m2﹣mn﹣36=9×22﹣2×2﹣36=﹣4.
故选:D.
7.【思路点拨】将所求的代数式适当变形,利用整体代入的思想解答即可.
【答案】解:原式=3﹣4x﹣6y
=3﹣2(2x+3y).
∵2x+3y+1=4,
∴2x+3y=3
∴原式=3﹣2×3=﹣3.
故选:D.
8.【思路点拨】根据多项式及其次数的定义、绝对值解决此题.
【答案】解:由题意得:k﹣2≠0且|k|﹣2=0.
∴k≠2且k=±2.
∴k=﹣2.
故选:B.
9.【思路点拨】将x=3代入代数式中,得到关于p,q的式子,再将x=﹣3代入代数式并整理,利用整体代入的方法解答即可得出结论.
【答案】解:∵当x=3时,代数式px3+qx﹣1的值为4,
∴27p+3q﹣1=4,
∴27p+3q=5.
∴当x=﹣3时,
px3+qx﹣1
=﹣27p﹣3p﹣1
=﹣(27p+3q)﹣1
=﹣5﹣1
=﹣6.
故选:B.
10.【思路点拨】先将两式相加,合并同类项,再令x2项的系数为0,即可解除m.
【答案】解:∵4x2﹣3x+7+5x3+(m﹣2)x2﹣2x+3=5x3+(m+2)x2﹣5x+10,
而4x2﹣3x+7与多项式5x3+(m﹣2)x2﹣2x+3相加后,结果不含x2项,
∴m+2=0,
∴m=﹣2,
故选:A.
选题题
11.【思路点拨】a的3倍即为3a,b的平方即为b2,再将两者作差即可得.
【答案】解:“a的3倍与b的平方的差”用代数式表示为3a﹣b2,
故答案为:3a﹣b2.
【点睛】本题主要考查列代数式,列代数式应该注意的四个问题
1.在同一个式子或具体问题中,每一个字母只能代表一个量.
2.要注意书写的规范性.用字母表示数以后,在含有字母与数字的乘法中,通常将“×”简写作“ ”或者省略不写.
3.在数和表示数的字母乘积中,一般把数写在字母的前面,这个数若是带分数要把它化成假分数.
4.含有字母的除法,一般不用“÷”(除号),而是写成分数的形式.
12.【思路点拨】根据几个单项式的和叫做多项式,每个单项式叫做多项式的项,其中不含字母的项叫做常数项.多项式中次数最高的项的次数叫做多项式的次数,如果一个多项式含有a个单项式,次数是b,那么这个多项式就叫b次a项式可得答案.
【答案】解:多项式2a3b+3b﹣l是四次三项式,其中常数项为﹣1,
故答案为:四;三;﹣1.
13.【思路点拨】根据单项式的系数与次数的定义解决此题.
【答案】解:∵单项式﹣x3y2z的系数为﹣1,次数为6,
∴α=﹣1,b=6.
∴α+b=﹣1+6=5.
故答案为:5.
14.【思路点拨】根据多项式的项及次数的概念进行分析解答.
【答案】解:多项式a2b+2ab4﹣38含有a2b、2ab4、﹣38三项,其中2ab4的次数最高为五次,
∴多项式a2b+2ab4﹣38是五次三项式,
故答案为:五、三.
15.【思路点拨】根据同类项的定义(所含字母相同,相同字母的指数相同)即可解答.
【答案】解:∵代数式﹣2a3bm与4an+1b4是同类项,
∴n+1=3,m=4,
解得m=4,n=2,
∴m+n=4+2=6.
故答案为:6.
16.【思路点拨】根据售价=标价×0.7列式即可.
【答案】解:根据题意得,这种商品每件的售价为0.7a元.
故答案为:0.7a元.
17.【思路点拨】根据数轴可确定a、b、c的符号与绝对值的大小,从而可以去掉绝对值符号进行化简.
【答案】解:由题意得,
c<a<0<b,且|c|>|a|>|b|,
∴a+c<0,a﹣b<0,b﹣c>0,
∴|a+c|﹣|a﹣b|+|b﹣c|
=﹣(a+c)﹣[﹣(a﹣b)]+b﹣c
=﹣a﹣c+a﹣b+b﹣c
=﹣2c,
故答案为:﹣2c.
18.【思路点拨】直接利用整式的加减运算法则化简,进而得出a,b的值,进而得出答案.
【答案】解:∵代数式(2x2+ax﹣y+6)﹣(2bx2﹣3x﹣5y﹣1)的值与字母x的取值无关,
∴(2x2+ax﹣y+6)﹣(2bx2﹣3x﹣5y﹣1)
=2x2+ax﹣y+6﹣2bx2+3x+5y+1
=(2﹣2b)x2+(a+3)x+4y+7,
∴2﹣2b=0,a+3=0,
解得:b=1,a=﹣3,
∴a2b=(﹣3)2=9.
故答案为:9.
19.思路点拨】直接去括号,再合并同类项得出答案.
【答案】解:∵(﹣x2+3xy﹣y2)﹣2(﹣x2+4xy﹣y2)=﹣5xy+y2,
∴﹣x2+3xy﹣y2+5x2﹣8xy+3y2=﹣5xy+y2,
4x2﹣5xy+y2=﹣5xy+y2,
故被墨汁遮住的一项应是4x2.
故答案为:4x2.
20.【思路点拨】根据每个单项式的系数的符号,系数的绝对值以及x的次数与它排列的位数的关系即可得出结论.
【答案】解:∵观察多项式的排列发现如下规律:①奇数项为正,偶数项为负;②系数的绝对值从3开始依次相差4;③x的次数与它所在位置数相同,及第n个多项式中x的次数为n,
∴这样排列第n个单项式应是:(﹣1)n+1(4n﹣1)xn.
故答案为:(﹣1)n+1(4n﹣1)xn.
解答题
21.【思路点拨】(1)直接利用多项式以及单项式定义分析即可;
(2)直接利用多项式的次数确定方法分析得出答案;
(3)直接利用单项式的次数与系数确定方法分析即可.
【答案】解:(1)多项式:②④⑧;单项式:①⑤⑥;
(2)次数最高的多项式是二;
故答案为:二;
(3)次数最高的单项式的次数是4,系数是π.
故答案为:4,π.
22.【思路点拨】(1)首先去括号,再合并同类项即可.
(2)首先去小括号,再去中括号,再合并同类项即可.
(3)原式去括号合并即可得到结果;
(4)原式去括号合并即可得到结果.
【答案】解:(1)原式=4a2+18b﹣15a2﹣12b,
=﹣11a2+6b;
(2)原式=3x2﹣2(7x﹣4x+3﹣2x2),
=3x2﹣14x+8x﹣6+4x2,
=7x2﹣6x﹣6.
(3)原式=5ab+3a2﹣2a2﹣4ab=a2+ab;
(4)原式=8x2+3x+2x2﹣14x﹣10﹣3+4x=10x2﹣7x﹣13.
23.【思路点拨】(1)直接利用去括号法则判断得出错误原因;
(2)直接去括号,进而合并同类项得出答案.
【答案】解:(1)甲:(2x2﹣1+3x)﹣4(x﹣x2+1)
=2x2﹣1+3x﹣4x﹣4
=2x2﹣1+3x﹣4x+4x2﹣4;
乙:(2x2﹣1+3x)﹣4(x﹣x2+1)
=2x2﹣1+3x﹣4x+
=2x2﹣1+3x﹣4x+4x2﹣4;
(2)(2x2﹣1+3x)﹣4(x﹣x2+1)
=2x2﹣1+3x﹣4x+4x2﹣4
=6x2﹣x﹣5.
24.【思路点拨】根据整式的加减运算法则,先去括号,再计算加减,从而解决此题.
【答案】解:(□x2+6x+8)﹣(6x+5x2+2)
=□x2+6x+8﹣6x﹣5x2﹣2
=(□﹣5)x2+6.
∵该题标准答案的结果是常数,
∴□﹣5=0.
∴□=5.
25.【思路点拨】(1)将a=5,b=﹣1代入,再去括号、合并同类型即可得答案;
(2)先去括号、合并同类项,再根据计算的最后结果与x的取值无关列出关于a、b的方程,即可解得答案.
【答案】解:(1)∵a=5,b=﹣1,
∴(ax2+bx﹣1)﹣(4x2+3x)
=(5x2﹣x﹣1)﹣(4x2+3x)
=5x2﹣x﹣1﹣4x2﹣3x
=x2﹣4x﹣1;
(2)(ax2+bx﹣1)﹣(4x2+3x)
=ax2+bx﹣1﹣4x2﹣3x
=(a﹣4)x2+(b﹣3)x﹣1,
∵计算的最后结果与x的取值无关,
∴a﹣4=0,b﹣3=0,
∴a=4,b=3.
26.【思路点拨】(1)根据阴影部分的面积等于长方形ABCD的面积﹣边长为b的正方形面积即可得出结论;
(2)①根据长方形AGPH的面积是长方形ECNM面积的6.5倍列等式,可得答案;
②根据长方形PQMF的面积为2,列等式可得(a﹣2b)2=4,根据a<2b,得a﹣2b=﹣2,最后根据面积和可得答案.
【答案】解:(1)阴影部分的面积=a 4a﹣b2=4a2﹣b2;
(2)①∵AB=a,BG=b,
∴AG=a﹣b,
∵AD=BC=4a,DH=b,
∴AH=4a﹣b,
∵BE=a,BC=4a,
∴CE=4a﹣a=a,
∵长方形AGPH的面积是长方形ECNM面积的6.5倍,
∴(a﹣b)(4a﹣b)=6.5×a×(a﹣b),
∴3a=4b,
∴=;
②如图2,PQ=EF﹣EM=b﹣(a﹣b)=2b﹣a,
QM=QN﹣MN=b﹣a,
∵长方形PQMF的面积为2,
∴(2b﹣a)(b﹣a)=2,
(a﹣2b)2=4,
∴a﹣2b=±2,
∵a<2b,
∴a﹣2b<0,
∴a﹣2b=﹣2,
∴a=2b﹣2,
∴如图2中阴影部分的面积=长方形AGPH的面积+长方形ECNM的面积
=(a﹣b)(4a﹣b)+
=(a﹣b)(4a﹣b+a)
=(2b﹣2﹣b)(9b﹣9﹣b)
=(b﹣2)(8b﹣9)
=8b2﹣25b+18.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
