浙教版数学七年级上册期末测试 精品单元测试(含解析)
文档属性
| 名称 | 浙教版数学七年级上册期末测试 精品单元测试(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-25 13:53:16 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
苏教版七年级上册数学 期末测试 单元测试
【浙教版】
学校:___________姓名:___________班级:___________考号:___________
满分:120分 考试时间:120分钟
题号 一 二 三 总分
得分
选择题(本大题共10小题,每小题3分,共30分。下列各题的备选答案中,只有一项是最符合题意的,请选出。)
1.3的相反数是
A. B. 3 C. D.
2.下列各数中,属于有理数的是( )
A.π B. C.2.019 D.
3.如图,∠1的内错角是( )
A.∠2 B.∠3 C.∠4 D.∠5
4.下列方程中,属于一元一次方程的是( )
A.2x-1=0. B.1-x=y. C.. D.1-x2=0
5.小明记录了一星期每天的最低温度,如下表.
星期 一 二 三 四 五 六 日
温度 -2℃ -1℃ +2℃ +6℃ +4℃ +1℃ -3℃
这个星期的平均最低温度是( )摄氏度.
A.-1℃ B.0℃ C.+1℃ D.+2℃
6.平面内不同的两点确定一条直线,不同的三点最多确定三条直线,若在平面内的不同的n个点最多可确定36条直线,则n的值为( )
A.6 B.7 C.8 D.9
7.下列方程中变形正确的是( )
A.方程3x﹣2=2x﹣1移项,得3x﹣2x=﹣1﹣2
B.方程去分母,得5(x﹣1)﹣2x=1
C.方程3﹣x=2﹣5(x﹣1)去括号,得3﹣x=2﹣5x﹣1
D.方程系数化为1,得x=﹣1
8.下列各组单项式中,不是同类项的是( )
A.4m2y与 B.7x2n与﹣9xn2
C.3mnx2与 D.与
9.如图,现要从村庄A修建一条连接公路PQ的最短小路,过点A作AH⊥PQ于点H,沿AH修建公路,这样做的理由是( )
A.垂线段最短
B.两点之间,线段最短
C.过一点可以作无数条直线
D.两点确定一条直线
10.观察下面由正整数组成的数阵:
照此规律,按从上到下、从左到右的顺序,第51行的第1个数是( )
A.2500 B.2501 C.2601 D.2602
填空题(本大题共10小题,每小题4分,共40分。)
8的立方根是___.
单项式的次数是______.
13.某校七年级(1)班有女生人,男生比女生的2倍少7人,则用含的代数式表示男生的人数为______.
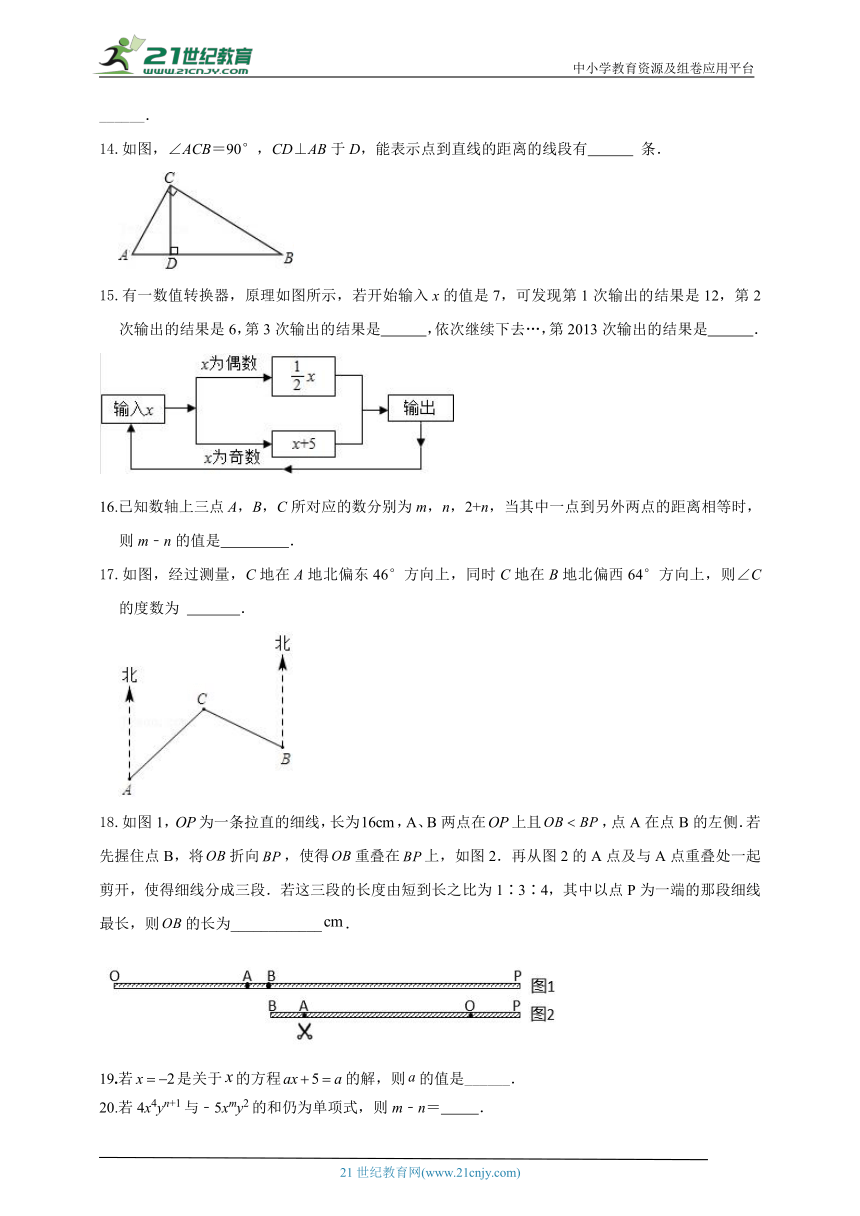
14.如图,∠ACB=90°,CD⊥AB于D,能表示点到直线的距离的线段有 条.
15.有一数值转换器,原理如图所示,若开始输入x的值是7,可发现第1次输出的结果是12,第2次输出的结果是6,第3次输出的结果是 ,依次继续下去…,第2013次输出的结果是 .
16.已知数轴上三点A,B,C所对应的数分别为m,n,2+n,当其中一点到另外两点的距离相等时,则m﹣n的值是 .
17.如图,经过测量,C地在A地北偏东46°方向上,同时C地在B地北偏西64°方向上,则∠C的度数为 .
18.如图1,为一条拉直的细线,长为,A、B两点在上且,点A在点B的左侧.若先握住点B,将折向,使得重叠在上,如图2.再从图2的A点及与A点重叠处一起剪开,使得细线分成三段.若这三段的长度由短到长之比为1∶3∶4,其中以点P为一端的那段细线最长,则的长为____________.
19.若是关于的方程的解,则的值是______.
20.若4x4yn+1与﹣5xmy2的和仍为单项式,则m﹣n= .
三、解答题(本大题共6小题,前5小题每小题8分,第6小题10分,共50分。解答应写出文字说明、证明过程或演算步骤.)
21.计算:
(1)4+(﹣3)2×2. (2)×6.
22.先化简,再求值;3(x2﹣3y)﹣(3x2+y﹣x),其中x=﹣2,y=.
23.图①、图②、图③均是4×4的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点称为格点,点A、B、C均为格点.只用无刻度的直尺,分别在给定的网格中找一格点M,按下列要求作图:
(1)在图①中,连结MA、MB,使MA=MB;
(2)在图②中,连结MA、MB、MC,使MA=MB=MC;
(3)在图③中,连结MA、MC,使∠AMC=2∠ABC.
24.观察下面三行数:
2,﹣4,8,﹣16,32,﹣64,…; ①
4,﹣2,10,﹣14,34,﹣62,…; ②
1,﹣2,4,﹣8,16,﹣32,….③
如图,在上面的数据中,用一个长方形圈出同一列的三个数,这列的第一个数表示为a,其余各数分别用a,b,c表示.
(1)若这三个数分别在这三行数的第n列,请用含n的式子分别表示a、b、c的值.
a= ,b= ,c= ;
(2)若a记为x,求a、b、c这三个数的和(结果用含x的式子表示并化简).
25.有20袋大米,以每袋30千克为标准,超过或不足的千克数分别用正负数来表述,记录如下:
与标准质量的差值(单位:千克) ﹣3 1 0 2.5 ﹣2 ﹣1.5
袋数 1 2 3 8 4 2
(1)20袋大米中,最重的一袋比最轻的一袋重多少千克?
(2)与标准重量比较,20袋大米总计超过多少千克或不足多少千克?
(3)若大米每千克售价3.5元,出售这20袋大米可卖多少元?
26.华联超市第一次用7000元购进甲、乙两种商品,其中甲商品的件数是乙商品件数的2倍,甲、乙两种商品的进价和售价如表:(注:获利=售价﹣进价)
甲 乙
进价(元/件) 20 30
售价(元/件) 25 40
(1)该超市购进甲、乙两种商品各多少件?
(2)该超市将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润?
(3)该超市第二次以第一次的进价又购进甲、乙两种商品,其中甲商品的件数不变,乙商品的件数是第一次的3倍:甲商品按原价销售,乙商品打折销售,第二次两种商品都售完以后获得的总利润比第一次获得的总利润多800元,求第二次乙商品是按原价打几折销售?
参考答案
选择题
1.【答案】A
【解析】解:3的相反数是
故选:
依据相反数的定义回答即可.
2.【答案】C
【分析】此题考察有理数的定义,即整数和分数都是有理数,依此即可判断.
【详解】是无限不循环小数,不是有理数,故A不选;
是无理数,不是有理数,故B不选;
2.019属于有理数,故C选;
是无理数不是有理数,故D不选.
故此题选D.
3.【答案】D
试题分析:根据内错角位于截线异侧,位于两条被截线之间可知∠1的内错角是∠5.
故选D.
4.【答案】A
【分析】根据一元一次方程的定义即可判断.
【详解】2x-1=0是一元一次方程,故A正确;
1-x=y中含有两个未知数,故不是一元一次方程,故B不选;
中x的次数不是1,故不选C;
1-x2=0中x的次数是2,故D不选.
故选A.
5.【答案】C
【分析】求出7天的温度值的平均数即可得到答案.
【详解】()
故选C.
6.【分析】根据平面内不同的两点确定一条直线,不同的三点最多确定三条直线…依此类推找出规律,用代数式表示出来,再将36代入所得的代数式进行计算.
【解答】解:∵平面内不同的两点确定1条直线,可表示为:=1;
平面内不同的三点最多确定3条直线,可表示为:=3;
平面内不同的四点确定6条直线,可表示为:=6;以此类推,可得:
平面内不同的n点可确定(n≥2)条直线.由已知可得:=36,
解得n=﹣8(舍去)或n=9.
故选:D.
7.【分析】各项中方程变形得到结果,即可作出判断.
【解答】解:由3x﹣2=2x﹣1移项,得3x﹣2x=﹣1+2,不符合题意;
B、由去分母,得5(x﹣1)﹣2x=1,符合题意;
C、由3﹣x=2﹣5(x﹣1)去括号,得3﹣x=2﹣5x+5,不符合题意;
D、由系数化为1,得x=﹣,不符合题意.
故选:B.
8【分析】根据同类项的定义(所含字母相同,相同字母的指数相同)判断即可.
【解答】解:A、4m2y与,所含字母相同,相同字母的指数相同,是同类项,故本选项不符合题意;
B、7x2n与﹣9xn2,所含字母相同,但相同字母的指数不相同,所以不是同类项,故本选项符合题意;
C、3mnx2与,所含字母相同,相同字母的指数相同,是同类项,故本选项不符合题意;
D、和,所含字母相同,相同字母的指数相同,是同类项,故本选项不符合题意;
故选:B.
9.【分析】根据垂线段的性质:垂线段最短,进行判断即可.
【解答】解:∵从直线外一点到这条直线上各点所连线段中,垂线段最短,
∴过点A作AH⊥PQ于点H,这样做的理由是垂线段最短.
故选:A.
10.【分析】观察数阵可知第n行最后一个数是n2,第n+1行第一个数就是n2+1,按此规律计算第51行第一个数即可.
【解答】解:观察数阵可知第n行最后一个数是n2,第n+1行第一个数就是n2+1,
∴第51行第一个数就是502+1=2501,
故选:B.
填空题
11.【答案】2
【分析】利用立方根的定义计算即可得到结果.
【详解】解:8的立方根为2,
故答案为:2.
12.【答案】6
【分析】根据单项式次数的定义解答即可.
【详解】解:单项式的次数是6.
故答案为:6.
13.【答案】
【分析】根据题意列出代数式即可.
【详解】某校七年级(1)班有女生人,男生比女生的2倍少7人,则男生的人数为()人
故答案为:
14.【分析】根据点到直线的距离的定义,得结论.
【解答】解:点C到AB的距离是线段CD,
点B到CD的距离是线段BD,
点A到CD的距离是线段AD,
点A到CB的距离是线段CA,
点B到AC的距离是线段BC,
故答案为:5
15.【分析】由输入x为7是奇数,得到输出的结果为x+5,将偶数12代入x代入计算得到结果为6,将偶数6代入x计算得到第3次的输出结果,依此类推得到一般性规律,即可得到第2013次的结果.
【解答】解:根据题意得:开始输入x的值是7,可发现第1次输出的结果是7+5=12;
第2次输出的结果是×12=6;
第3次输出的结果是×6=3;
第4次输出的结果为3+5=8;
第5次输出的结果为×8=4;
第6次输出的结果为×4=2;
第7次输出的结果为×2=1;
第8次输出的结果为1+5=6;
归纳总结得到输出的结果从第2次开始以6,3,8,4,2,1循环,
∵(2013﹣1)÷6=335…2,
则第2013次输出的结果为3.
故答案为:3;3
16.【分析】方向角是从正北或正南方向到目标方向所形成的小于90°的角,根据平行线的性质求得∠ACF与∠BCF的度数,∠ACF与∠BCF的和即为∠C的度数.
【解答】解:由题意作图如下
∠DAC=46°,∠CBE=64°,
由平行线的性质可得
∠ACF=∠DAC=46°,∠BCF=∠CBE=64°,
∴∠ACB=∠ACF+∠BCF=46°+64°=110°,
故答案:110°.
18.【分析】
根据题意可知剪断后的三段可以表示为OA、2AB、PB-AB,而根据题设可设三段分别为m,3m,4m,由总长度为16cm求出m的值,再分两种情况讨论OA=m或OA=3m,从而求出各线段的长.
【解答】
解:由题意可知剪断后的三段可以表示为OA、2AB、PB-AB,
而这三段的长度由短到长之比为1:3:4,于是可设三段分别为m,3m,4m
∵OA+2AB+PB-AB=OP=16
即m+3m+4m=16
∴m=2
∴剪断后的三条线段的长分别为2cm,6cm,8cm
又∵以点P为一端的那段细线最长
∴PB-AB=8,于是分类
若OA=2,则2AB=6,PB-AB=8
∴AB=3,PB=11
此时OB=OA+AB=5
若2AB=2,则OA=6,PB-AB=8
∴OA=6,AB=1,PB=9
此时OB=OA+AB=7
综上,OB的长为5或7
故答案为:5或7.
19.【答案】
【分析】直接把的值代入进而得出答案.
【详解】解:∵是方程的解,
∴,
解得:.
故答案为:.
20.【分析】根据同类项的定义(所含字母相同,相同字母的指数相同)列出方程,求出n,m的值,再代入代数式计算即可.
【解答】解:根据题意得:m=4,n+1=2,
解得:n=1,
则m﹣n=4﹣1=3.
故答案是:3.
解答题
21.【答案】(1)22;(2)8
【分析】(1)先算乘方,再算乘法,最后算加法;
(2)运用乘法分配律的逆运算计算.
【详解】解:(1)原式;
(2)原式.
22.【答案】,-7
【分析】先去括号,再合并同类项化为最简,再把、的值代入即可得出答案.
【详解】解:原式
,
把,代入上式,
原式.
23.【分析】(1)根据勾股定理得MA=MB=.
(2)连接AC,取AC中点M,MA=MB=MC=.
(3)取△ABC外心M,由圆周角定理得∠AMC=2∠ABC.
【解答】解:如图,
24.【分析】(1)由第①行第n个数为﹣(﹣2)n,而第②行第n个数是第①行相应数字与2的和,第③行第n个数是第①行相应数字的,据此可得;
(2)由(1)中所得规律可得若a=x、b=x+2、c=x,代入计算可得.
【解答】解:(1)由数列知a=﹣(﹣2)n、b=﹣(﹣2)n+2,c=,
故答案为:﹣(﹣2)n、﹣(﹣2)n+2、;
(2)若a=x,则b=x+2、c=x,
根据题意,得:a+b+c=x+x+2+x=x+2.
25.【分析】(1)根据表格中的数据可以求得20袋大米中,最重的一袋比最轻的一袋重多少千克;
(2)根据表格中的数据可以求得与标准重量比较,20袋大米总计超过或不足多少千克;
(3)根据题意和(2)中的结果可以解答本题.
【解答】解:(1)最重的一袋比最轻的一袋重:2.5﹣(﹣3)=2.5+3=5.5(千克),
答:最重的一袋比最轻的一袋重5.5千克;
(2)(﹣3)×1+(﹣2)×4+(﹣1.5)×2+1×2+0×3+2.5×8=8(千克),
答:20 袋大米总计超过8千克;
(3)3.5×(30×20+8)=2128(元),
答:出售这 20 袋大米可卖2128元.
26.【分析】
(1)设第一次购进乙种商品x件,则购进甲种商品2x件,根据题意列出方程即可求出答案;
(2)根据利润等于单件利润乘以售出件数即可求出答案.
(3)根据题意列出方程即可求出答案.
【解答】
解:(1)设第一次购进乙种商品x件,则购进甲种商品2x件,
根据题意得:20×2x+30x=7000,
解得:x=100,
∴2x=200件,
答:该超市第一次购进甲种商品100件,乙种商品200件.
(2)(25﹣20)×200+(40﹣30)×100=2000(元)
答:该超市将第一次购进的甲、乙两种商品全部卖完后一共可获得利润2000元.
(3)设第二次乙种商品是按原价打y折销售;
根据题意得:(25﹣20)×200+(40×﹣30)×100×3=2000+800,
解得:y=9
答:第二次乙商品是按原价打9折销售.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
苏教版七年级上册数学 期末测试 单元测试
【浙教版】
学校:___________姓名:___________班级:___________考号:___________
满分:120分 考试时间:120分钟
题号 一 二 三 总分
得分
选择题(本大题共10小题,每小题3分,共30分。下列各题的备选答案中,只有一项是最符合题意的,请选出。)
1.3的相反数是
A. B. 3 C. D.
2.下列各数中,属于有理数的是( )
A.π B. C.2.019 D.
3.如图,∠1的内错角是( )
A.∠2 B.∠3 C.∠4 D.∠5
4.下列方程中,属于一元一次方程的是( )
A.2x-1=0. B.1-x=y. C.. D.1-x2=0
5.小明记录了一星期每天的最低温度,如下表.
星期 一 二 三 四 五 六 日
温度 -2℃ -1℃ +2℃ +6℃ +4℃ +1℃ -3℃
这个星期的平均最低温度是( )摄氏度.
A.-1℃ B.0℃ C.+1℃ D.+2℃
6.平面内不同的两点确定一条直线,不同的三点最多确定三条直线,若在平面内的不同的n个点最多可确定36条直线,则n的值为( )
A.6 B.7 C.8 D.9
7.下列方程中变形正确的是( )
A.方程3x﹣2=2x﹣1移项,得3x﹣2x=﹣1﹣2
B.方程去分母,得5(x﹣1)﹣2x=1
C.方程3﹣x=2﹣5(x﹣1)去括号,得3﹣x=2﹣5x﹣1
D.方程系数化为1,得x=﹣1
8.下列各组单项式中,不是同类项的是( )
A.4m2y与 B.7x2n与﹣9xn2
C.3mnx2与 D.与
9.如图,现要从村庄A修建一条连接公路PQ的最短小路,过点A作AH⊥PQ于点H,沿AH修建公路,这样做的理由是( )
A.垂线段最短
B.两点之间,线段最短
C.过一点可以作无数条直线
D.两点确定一条直线
10.观察下面由正整数组成的数阵:
照此规律,按从上到下、从左到右的顺序,第51行的第1个数是( )
A.2500 B.2501 C.2601 D.2602
填空题(本大题共10小题,每小题4分,共40分。)
8的立方根是___.
单项式的次数是______.
13.某校七年级(1)班有女生人,男生比女生的2倍少7人,则用含的代数式表示男生的人数为______.
14.如图,∠ACB=90°,CD⊥AB于D,能表示点到直线的距离的线段有 条.
15.有一数值转换器,原理如图所示,若开始输入x的值是7,可发现第1次输出的结果是12,第2次输出的结果是6,第3次输出的结果是 ,依次继续下去…,第2013次输出的结果是 .
16.已知数轴上三点A,B,C所对应的数分别为m,n,2+n,当其中一点到另外两点的距离相等时,则m﹣n的值是 .
17.如图,经过测量,C地在A地北偏东46°方向上,同时C地在B地北偏西64°方向上,则∠C的度数为 .
18.如图1,为一条拉直的细线,长为,A、B两点在上且,点A在点B的左侧.若先握住点B,将折向,使得重叠在上,如图2.再从图2的A点及与A点重叠处一起剪开,使得细线分成三段.若这三段的长度由短到长之比为1∶3∶4,其中以点P为一端的那段细线最长,则的长为____________.
19.若是关于的方程的解,则的值是______.
20.若4x4yn+1与﹣5xmy2的和仍为单项式,则m﹣n= .
三、解答题(本大题共6小题,前5小题每小题8分,第6小题10分,共50分。解答应写出文字说明、证明过程或演算步骤.)
21.计算:
(1)4+(﹣3)2×2. (2)×6.
22.先化简,再求值;3(x2﹣3y)﹣(3x2+y﹣x),其中x=﹣2,y=.
23.图①、图②、图③均是4×4的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点称为格点,点A、B、C均为格点.只用无刻度的直尺,分别在给定的网格中找一格点M,按下列要求作图:
(1)在图①中,连结MA、MB,使MA=MB;
(2)在图②中,连结MA、MB、MC,使MA=MB=MC;
(3)在图③中,连结MA、MC,使∠AMC=2∠ABC.
24.观察下面三行数:
2,﹣4,8,﹣16,32,﹣64,…; ①
4,﹣2,10,﹣14,34,﹣62,…; ②
1,﹣2,4,﹣8,16,﹣32,….③
如图,在上面的数据中,用一个长方形圈出同一列的三个数,这列的第一个数表示为a,其余各数分别用a,b,c表示.
(1)若这三个数分别在这三行数的第n列,请用含n的式子分别表示a、b、c的值.
a= ,b= ,c= ;
(2)若a记为x,求a、b、c这三个数的和(结果用含x的式子表示并化简).
25.有20袋大米,以每袋30千克为标准,超过或不足的千克数分别用正负数来表述,记录如下:
与标准质量的差值(单位:千克) ﹣3 1 0 2.5 ﹣2 ﹣1.5
袋数 1 2 3 8 4 2
(1)20袋大米中,最重的一袋比最轻的一袋重多少千克?
(2)与标准重量比较,20袋大米总计超过多少千克或不足多少千克?
(3)若大米每千克售价3.5元,出售这20袋大米可卖多少元?
26.华联超市第一次用7000元购进甲、乙两种商品,其中甲商品的件数是乙商品件数的2倍,甲、乙两种商品的进价和售价如表:(注:获利=售价﹣进价)
甲 乙
进价(元/件) 20 30
售价(元/件) 25 40
(1)该超市购进甲、乙两种商品各多少件?
(2)该超市将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润?
(3)该超市第二次以第一次的进价又购进甲、乙两种商品,其中甲商品的件数不变,乙商品的件数是第一次的3倍:甲商品按原价销售,乙商品打折销售,第二次两种商品都售完以后获得的总利润比第一次获得的总利润多800元,求第二次乙商品是按原价打几折销售?
参考答案
选择题
1.【答案】A
【解析】解:3的相反数是
故选:
依据相反数的定义回答即可.
2.【答案】C
【分析】此题考察有理数的定义,即整数和分数都是有理数,依此即可判断.
【详解】是无限不循环小数,不是有理数,故A不选;
是无理数,不是有理数,故B不选;
2.019属于有理数,故C选;
是无理数不是有理数,故D不选.
故此题选D.
3.【答案】D
试题分析:根据内错角位于截线异侧,位于两条被截线之间可知∠1的内错角是∠5.
故选D.
4.【答案】A
【分析】根据一元一次方程的定义即可判断.
【详解】2x-1=0是一元一次方程,故A正确;
1-x=y中含有两个未知数,故不是一元一次方程,故B不选;
中x的次数不是1,故不选C;
1-x2=0中x的次数是2,故D不选.
故选A.
5.【答案】C
【分析】求出7天的温度值的平均数即可得到答案.
【详解】()
故选C.
6.【分析】根据平面内不同的两点确定一条直线,不同的三点最多确定三条直线…依此类推找出规律,用代数式表示出来,再将36代入所得的代数式进行计算.
【解答】解:∵平面内不同的两点确定1条直线,可表示为:=1;
平面内不同的三点最多确定3条直线,可表示为:=3;
平面内不同的四点确定6条直线,可表示为:=6;以此类推,可得:
平面内不同的n点可确定(n≥2)条直线.由已知可得:=36,
解得n=﹣8(舍去)或n=9.
故选:D.
7.【分析】各项中方程变形得到结果,即可作出判断.
【解答】解:由3x﹣2=2x﹣1移项,得3x﹣2x=﹣1+2,不符合题意;
B、由去分母,得5(x﹣1)﹣2x=1,符合题意;
C、由3﹣x=2﹣5(x﹣1)去括号,得3﹣x=2﹣5x+5,不符合题意;
D、由系数化为1,得x=﹣,不符合题意.
故选:B.
8【分析】根据同类项的定义(所含字母相同,相同字母的指数相同)判断即可.
【解答】解:A、4m2y与,所含字母相同,相同字母的指数相同,是同类项,故本选项不符合题意;
B、7x2n与﹣9xn2,所含字母相同,但相同字母的指数不相同,所以不是同类项,故本选项符合题意;
C、3mnx2与,所含字母相同,相同字母的指数相同,是同类项,故本选项不符合题意;
D、和,所含字母相同,相同字母的指数相同,是同类项,故本选项不符合题意;
故选:B.
9.【分析】根据垂线段的性质:垂线段最短,进行判断即可.
【解答】解:∵从直线外一点到这条直线上各点所连线段中,垂线段最短,
∴过点A作AH⊥PQ于点H,这样做的理由是垂线段最短.
故选:A.
10.【分析】观察数阵可知第n行最后一个数是n2,第n+1行第一个数就是n2+1,按此规律计算第51行第一个数即可.
【解答】解:观察数阵可知第n行最后一个数是n2,第n+1行第一个数就是n2+1,
∴第51行第一个数就是502+1=2501,
故选:B.
填空题
11.【答案】2
【分析】利用立方根的定义计算即可得到结果.
【详解】解:8的立方根为2,
故答案为:2.
12.【答案】6
【分析】根据单项式次数的定义解答即可.
【详解】解:单项式的次数是6.
故答案为:6.
13.【答案】
【分析】根据题意列出代数式即可.
【详解】某校七年级(1)班有女生人,男生比女生的2倍少7人,则男生的人数为()人
故答案为:
14.【分析】根据点到直线的距离的定义,得结论.
【解答】解:点C到AB的距离是线段CD,
点B到CD的距离是线段BD,
点A到CD的距离是线段AD,
点A到CB的距离是线段CA,
点B到AC的距离是线段BC,
故答案为:5
15.【分析】由输入x为7是奇数,得到输出的结果为x+5,将偶数12代入x代入计算得到结果为6,将偶数6代入x计算得到第3次的输出结果,依此类推得到一般性规律,即可得到第2013次的结果.
【解答】解:根据题意得:开始输入x的值是7,可发现第1次输出的结果是7+5=12;
第2次输出的结果是×12=6;
第3次输出的结果是×6=3;
第4次输出的结果为3+5=8;
第5次输出的结果为×8=4;
第6次输出的结果为×4=2;
第7次输出的结果为×2=1;
第8次输出的结果为1+5=6;
归纳总结得到输出的结果从第2次开始以6,3,8,4,2,1循环,
∵(2013﹣1)÷6=335…2,
则第2013次输出的结果为3.
故答案为:3;3
16.【分析】方向角是从正北或正南方向到目标方向所形成的小于90°的角,根据平行线的性质求得∠ACF与∠BCF的度数,∠ACF与∠BCF的和即为∠C的度数.
【解答】解:由题意作图如下
∠DAC=46°,∠CBE=64°,
由平行线的性质可得
∠ACF=∠DAC=46°,∠BCF=∠CBE=64°,
∴∠ACB=∠ACF+∠BCF=46°+64°=110°,
故答案:110°.
18.【分析】
根据题意可知剪断后的三段可以表示为OA、2AB、PB-AB,而根据题设可设三段分别为m,3m,4m,由总长度为16cm求出m的值,再分两种情况讨论OA=m或OA=3m,从而求出各线段的长.
【解答】
解:由题意可知剪断后的三段可以表示为OA、2AB、PB-AB,
而这三段的长度由短到长之比为1:3:4,于是可设三段分别为m,3m,4m
∵OA+2AB+PB-AB=OP=16
即m+3m+4m=16
∴m=2
∴剪断后的三条线段的长分别为2cm,6cm,8cm
又∵以点P为一端的那段细线最长
∴PB-AB=8,于是分类
若OA=2,则2AB=6,PB-AB=8
∴AB=3,PB=11
此时OB=OA+AB=5
若2AB=2,则OA=6,PB-AB=8
∴OA=6,AB=1,PB=9
此时OB=OA+AB=7
综上,OB的长为5或7
故答案为:5或7.
19.【答案】
【分析】直接把的值代入进而得出答案.
【详解】解:∵是方程的解,
∴,
解得:.
故答案为:.
20.【分析】根据同类项的定义(所含字母相同,相同字母的指数相同)列出方程,求出n,m的值,再代入代数式计算即可.
【解答】解:根据题意得:m=4,n+1=2,
解得:n=1,
则m﹣n=4﹣1=3.
故答案是:3.
解答题
21.【答案】(1)22;(2)8
【分析】(1)先算乘方,再算乘法,最后算加法;
(2)运用乘法分配律的逆运算计算.
【详解】解:(1)原式;
(2)原式.
22.【答案】,-7
【分析】先去括号,再合并同类项化为最简,再把、的值代入即可得出答案.
【详解】解:原式
,
把,代入上式,
原式.
23.【分析】(1)根据勾股定理得MA=MB=.
(2)连接AC,取AC中点M,MA=MB=MC=.
(3)取△ABC外心M,由圆周角定理得∠AMC=2∠ABC.
【解答】解:如图,
24.【分析】(1)由第①行第n个数为﹣(﹣2)n,而第②行第n个数是第①行相应数字与2的和,第③行第n个数是第①行相应数字的,据此可得;
(2)由(1)中所得规律可得若a=x、b=x+2、c=x,代入计算可得.
【解答】解:(1)由数列知a=﹣(﹣2)n、b=﹣(﹣2)n+2,c=,
故答案为:﹣(﹣2)n、﹣(﹣2)n+2、;
(2)若a=x,则b=x+2、c=x,
根据题意,得:a+b+c=x+x+2+x=x+2.
25.【分析】(1)根据表格中的数据可以求得20袋大米中,最重的一袋比最轻的一袋重多少千克;
(2)根据表格中的数据可以求得与标准重量比较,20袋大米总计超过或不足多少千克;
(3)根据题意和(2)中的结果可以解答本题.
【解答】解:(1)最重的一袋比最轻的一袋重:2.5﹣(﹣3)=2.5+3=5.5(千克),
答:最重的一袋比最轻的一袋重5.5千克;
(2)(﹣3)×1+(﹣2)×4+(﹣1.5)×2+1×2+0×3+2.5×8=8(千克),
答:20 袋大米总计超过8千克;
(3)3.5×(30×20+8)=2128(元),
答:出售这 20 袋大米可卖2128元.
26.【分析】
(1)设第一次购进乙种商品x件,则购进甲种商品2x件,根据题意列出方程即可求出答案;
(2)根据利润等于单件利润乘以售出件数即可求出答案.
(3)根据题意列出方程即可求出答案.
【解答】
解:(1)设第一次购进乙种商品x件,则购进甲种商品2x件,
根据题意得:20×2x+30x=7000,
解得:x=100,
∴2x=200件,
答:该超市第一次购进甲种商品100件,乙种商品200件.
(2)(25﹣20)×200+(40﹣30)×100=2000(元)
答:该超市将第一次购进的甲、乙两种商品全部卖完后一共可获得利润2000元.
(3)设第二次乙种商品是按原价打y折销售;
根据题意得:(25﹣20)×200+(40×﹣30)×100×3=2000+800,
解得:y=9
答:第二次乙商品是按原价打9折销售.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
