浙教版数学七年级上册期中测试 精品单元测试(含解析)
文档属性
| 名称 | 浙教版数学七年级上册期中测试 精品单元测试(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-25 13:30:02 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
苏教版七年级上册数学 期中测试(1-4章) 单元测试
【浙教版】
学校:___________姓名:___________班级:___________考号:___________
满分:120分 考试时间:120分钟
题号 一 二 三 总分
得分
选择题(本大题共10小题,每小题3分,共30分。下列各题的备选答案中,只有一项是最符合题意的,请选出。)
1.的倒数是( )
A. B. C. D.
2.绝对值大于且小于的整数个数是( )
A. B. C. D.
3.若在单位长度的数轴上随意画出一条长的线段,则线段盖住的整数点至少有( )
A.9个 B.10个 C.100个 D.101个
4.若与是同一个数的两个不同的平方根,则m的值( )
A. B.1 C.或1 D.
5.若,则的值是( )
A.2 B.1 C. D.3
6.点A,B在数轴上的位置如图所示,其对应的有理数分别是a和b.对于下列四个结论:①;②;③;④;⑤.其中正确的是( )
A.①②③④ B.①②③⑤ C.①③⑤ D.②③④
7.某学校计划购买甲、乙两种品牌的电子白板共40台.甲、乙两种品牌电子白板的单价分别为2.5万元/台和1.5万元/台,若购买甲品牌电子白板费用为万元,则购买乙品牌电子白板费用为( )
A.万元 B.万元 C.万元 D.万元
8.如图,在一个正方形的内部放置大小不同的两个小正方形,其中较大的正方形的面积为11,较小的正方形的面积为4,中间重叠部分的面积为1,则图中三角形的面积为( )
A.11 B.10 C.6 D.5
9.为了求的值,可令,则,因此,所以,仿照以上推理计算出的值是( )
A. B. C. D.
10.若规定“!”是一种数学运算符号,且1!=1,2!=2×1=2,3!=3×2×1=6,4!=4×3×2×1=24, ,则的值为( )
A.9900 B.99! C. D.2
填空题(本大题共10小题,每小题4分,共40分。)
11.绝对值是 .
12.目前,我国基本医疗保险覆盖已超过13500000000人,数据13500000000用科学记数法可以表示为 .
13.已知三个有理数、、,其积是负数,则 .
14.在计算两位数的平方运算时,我们可以利用“竖式”方式进行快速运算,其步骤如图所示(图1,2,3),现有一个两位数,其十位数字为,在进行平方运算时,部分步骤如图4所示(为小于的正整数),则这个两位数是 (用含的代数式表达).
15.在一条可以折叠的数轴上,A和B表示的数分别是和6,点C为A、B之间一点(不与A、B重合),以点C为折点,将此数轴向右对折,且,则C点表示的数是 .
16.比较大小: (填“”“”“”).
17.在这四个数中,任取两个数相乘,所得的积最大是 ,所得的积最小是 .
18.已知的立方根是3,,则= .
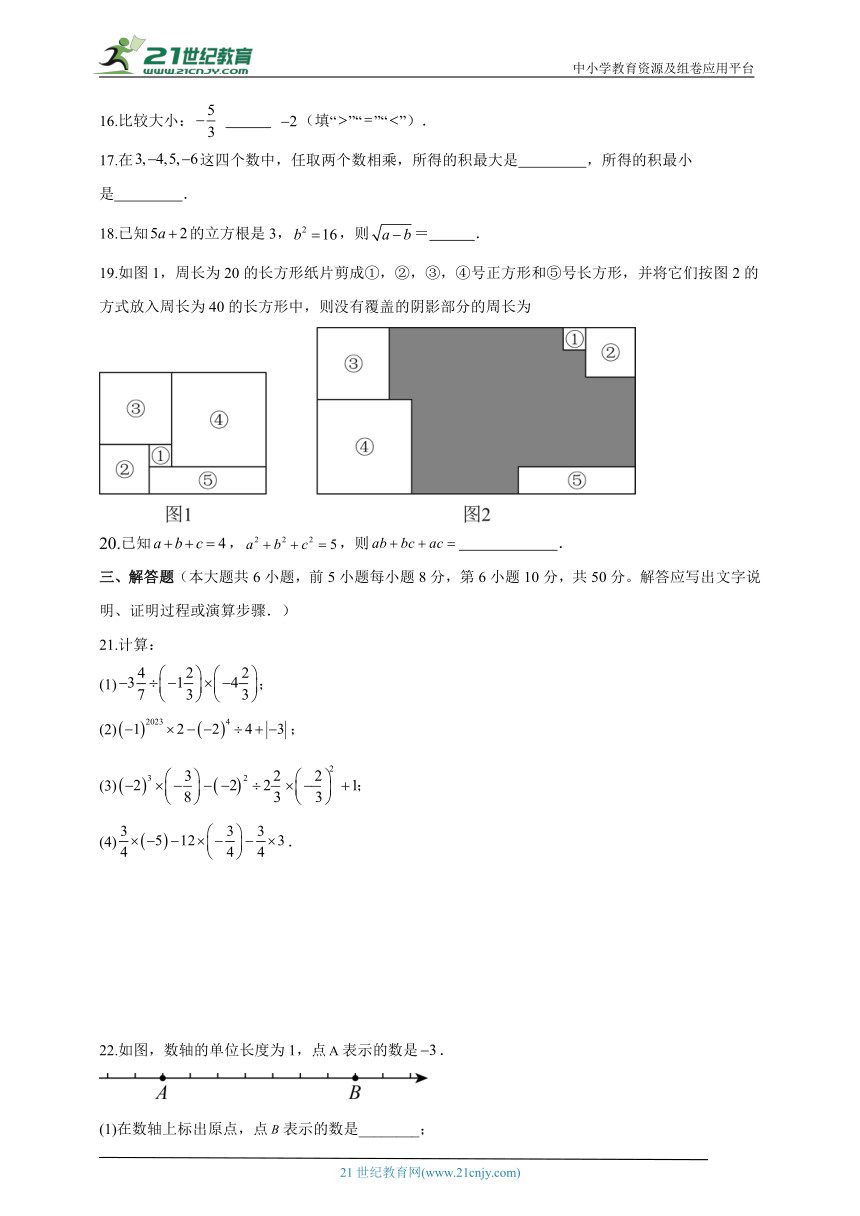
19.如图1,周长为20的长方形纸片剪成①,②,③,④号正方形和⑤号长方形,并将它们按图2的方式放入周长为40的长方形中,则没有覆盖的阴影部分的周长为
20.已知,,则 .
三、解答题(本大题共6小题,前5小题每小题8分,第6小题10分,共50分。解答应写出文字说明、证明过程或演算步骤.)
21.计算:
(1);
(2);
(3);
(4).
22.如图,数轴的单位长度为1,点表示的数是.
(1)在数轴上标出原点,点表示的数是________;
(2)在数轴上表示出下列各数:,,,,并将这些数及点,表示的数用“”号连接起来.
23.为了节省材料,某水产养殖户利用水库的岸堤(岸堤足够长)为一边, 用围网在水库中围成了如图所示的①、②、③三块长方形区域,其中区域①的一边长为a米,区域③长方形的长为b米, 是其宽的4倍.
(1)宽的长度为 米,围成养殖场围网的总长度为 米;
(2)当、时,求围网的总长度.
24.已知的立方根是,的平方根是.
(1)求的值.
(2)求的平方根.
25.某水果店以每箱200元的价格从水果批发市场购进20箱樱桃.若以每箱净重10千克为标准,超过的千克数记为正数,不足的千克数记为负数,称重的记录如下表:
与标准质量的差值(单位:千克) 0
箱数 1 4 3 4 5 3
(1)这20箱樱桃质量相差最大是多少千克?
(2)这20箱樱桃的总质量是多少千克?
(3)水果店购进这批樱桃需要付运费100元,要把这些樱桃全部以零售的形式卖掉,并按照全部销售后获得利润为成本的作为销售目标制定零售价,若第一天水果店以该零售价售出了总质量的,第二天因害怕剩余的樱桃腐烂,决定降价把剩余的樱桃按原零售价的七折售完,请计算该水果店在销售这批樱桃的过程中共盈利或亏损多少元?(提示:成本=总进价+运费)
26.阅读下面的文字,解答问题∶大家知道是无理数,而无理数是无限不循环小数,因此的小数部分我们不可能全部写出来.将这个数减去其整数部分,得到的差就是小数部分,因为的整数部分是1,于是用来表示的小数部分.又例如:
∵,即,
∴的整数部分是2,小数部分为.
根据上述材料,回答下列问题:
(1)的整数部分是___,小数部分是___.
(2)也是夹在相邻两个整数之间的,可以表示为,求的值;
(3)若的整数部分为x,小数部分为y,求的平方根.
参考答案
选择题
1.【答案】C
【分析】乘积为“1”的两个数互为倒数,根据定义解答即可.
【详解】解:∵,
∴的倒数是,
故选:C.
2.【答案】C
【分析】根据绝对值的定义解答即可.
【详解】解:绝对值大于且小于的所有整数是:,,共个.
故选:C.
3.【答案】C
【分析】分类讨论:线段的两端点是整数点,线段的两端点不是整数点,根据线段的长度,可得答案.
【详解】解:当线段的两端点是整数点时,一条长的线段,则被线段盖住的整数有个,
当线段的两端点不是整数点时,一条长的线段,则被线段盖住的整数有个,
线段盖住的整数点至少有个
故选:C.
4.【答案】B
【分析】根据一个正数的两个平方根互为相反数得到,即可求出m的值.
【详解】解:∵与是同一个数的两个不同的平方根,
∴,
∴,
故答案为:1.
5.【答案】C
【分析】原式变形后,将的值代入计算即可求出值.
【详解】解:∵,
∴原式,
故选:C.
6.【答案】B
【分析】由数轴可知:,据此即可求解.
【详解】解:由数轴可知:
①,故①正确;
②,∴,故②正确;
③,故③正确;
④,故④错误;
⑤,故⑤正确
故选:B
7.【答案】A
【分析】根据购买甲品牌电子白板费用为万元可得购买甲品牌电子白板台,可求出购买乙品牌电子白板的数量为台,再根据“单价×数量”可得结论.
【详解】解:∵甲品牌电子白板的单价分别为2.5万元/台,且购买甲品牌电子白板费用为万元,
∴购买甲品牌电子白板台,
∴购买乙品牌电子白板的数量为台,
∴购买乙品牌电子白板费用为万元
故选:A
8.【答案】D
【分析】观察图形可知,两个空白部分的长相等,宽也相等,则重叠部分也为正方形,根据较大的正方形的面积为11,较小的正方形的面积为4,中间重叠部分的面积为1,则较大的正方形的边长为,较小的正方形的边长为2,中间重叠部分的正方形边长为1;从而得出空白部分的长方形的较小边长为,继而得,,然后由求解即可.
【详解】解:观察图形可知,两个空白部分的长相等,宽也相等,
重叠部分也为正方形,
∵较大的正方形的面积为11,较小的正方形的面积为4,中间重叠部分的面积为1,
∴较大的正方形的边长为,较小的正方形的边长为2,中间重叠部分的正方形边长为1;
∴空白部分的长方形的较小边长为,
∴
∴
∴
故选:D.
9.【答案】D
【分析】本题通过题干给出的方法,可以设,然后用,得到M的解.
【详解】解:设 ,
故选:D.
10.【答案】A
【分析】先根据数学运算符号“!”得出和的值,再计算有理数的乘除法即可得.
【详解】由题意得:
故选:A.
填空题
11.【答案】
【分析】根据绝对值的意义解答即可.
【详解】解:负数的绝对值是它的相反数,
的绝对值是,
故答案为:.
12.【答案】
【分析】科学记数法的表示形式为的形式,其中,为整数.确定的值时,要看把原数变成时,小数点移动了多少位,的绝对值与小数点移动的位数相同.当原数绝对值时,是正整数;当原数的绝对值时,是负整数.
【详解】解:,
故答案为:.
13.【答案】或
【分析】根据题意可知,有两种情况:①、、均为负数;②、、中有一个负数,根据绝对值的意义化简求值,即可得到答案
【详解】解:由题意可知,,则有两种情况:
①、、均为负数,则
②、、中有一个负数,则,
故答案为:或
14.【答案】
【分析】观察图形可发现:“竖式”的第一行从左向右分别为:十位上的数字的平方与个位上的数字的平方,即中的是中的平方,中的是中的平方,每个数的平方占两个空,平方是一位数的前面的空用填补;第二行从左向右是这个两位数的个位上的数字与十位上的数字之积的倍,即是中,乘积为两位的填中间两个空格,乘积为三位数的从左边第一个空格开始填.以此规律即可解答.
【详解】解:根据题意可得,图1,竖式中第一行:中的是中的平方,中的是中的平方;第二行:是中;
图2,竖式中第一行:中的是中的平方,中的是中的平方;第二行:是中;
图3,竖式中第一行:中的是中的平方,中的是中的平方;第二行:是中;
∴图4中,第二行的这个两位数可表示为:,这个数是某个乘方数中十位上的数字与个位上的数字之积的倍,
∴这个两位数的十位上的数字与个位上的数字之积为:,
∵这个两位数的十位数字为,
∴这个两位数的个位数字为,
∴这个两位数是,
故答案为:.
15.【答案】或
【分析】设点C表示的数为x,根据点A表示的数为,点B表示的数为6,得到,,根据,或,且, 分类讨论即得.
【详解】设点C表示的数为x,
∵点A表示的数为,点B表示的数为6,
∴,,
∵,
∴,,
或,.
故答案为:或.
16.【答案】
【分析】按照两个负数比较大小的法则进行比较即可.
【详解】解:,
.
故答案为:.
17.【答案】 24
【分析】根据两数相乘,同号得正、异号得负求两数的积,再由正数大于负数,即可求解.
【详解】解:∵,
∴积最大是24,
∵,
∴积最小是,
故答案为:24,.
18.【答案】1或3/3或1
【分析】根据题意求出,的值,代入即可求解.
【详解】解:的立方根是3,
,
,
,
,
当,时,
;
当,时,
;
综上,的值为1或3,
故答案为:1或3.
19.【答案】30
【分析】在图1中,设①号正方形的边长为x,②号正方形的边长为y,则③号正方形的边长为,④号正方形的边长为,根据图1的周长求得,再根据图2的周长求得,进而可由没有覆盖的阴影部分的周长为求解即可.
【详解】解:在图1中,设①号正方形的边长为x,②号正方形的边长为y,则③号正方形的边长为,④号正方形的边长为,
由图1中长方形的周长为20得,
解得:,
如图2,
由图2中的长方形的周长为40得,
∴,
由图2得没有覆盖的阴影部分的周长为,
故答案为:30.
20.【答案】
【分析】将两边同时平方可得出,由可得出,从而即可得到答案.
【详解】解:,
,
,
,
,
,
,
故答案为:.
解答题
21.【答案】(1)
(2)
(3)
(4)3
【详解】(1)
;
(2)
;
(3)
;
(4)
.
22.【答案】(1)4
(2)见解析,
【分析】(1)根据的相对位置即可求解;
(2)先将各数化简,即可求解.
【详解】(1)解:∵点在点的右边,且距离点个单位长度
故点表示的数是:
故答案为:
(2)解:
在数轴上表示各数,如图所示:
由数轴可知:
23.【答案】(1);
(2)240
【分析】(1)根据图示得出的长,进而得出养殖场围网的总长度;
(2)把、代入代数式解答即可.
【详解】(1)解:∵长方形的长为b米, 是其宽的4倍.
∴,
∵为a米,
∴围成养殖场围网的总长度(米);
(2)把,代入(米),
答:围网的总长度为240米.
24.【答案】(1),
(2)
【分析】(1)根据平方根、立方根的定义可得,求解即可;
(2)将的值代入,然后根据平方根的定义求解即可.
【详解】(1)解:∵的立方根是,的平方根是.
∴,
解得:,;
(2)解:∵,,
∴,
∵的平方根是,
∴的平方根.
26.【答案】(1)这20箱樱桃质量相差最大是1.3千克
(2)这20箱樱桃的总质量是205千克
(3)该水果店销售这批樱桃共盈利1312元
【分析】(1)用与标准质量的差值中的最大值减去最小值进行求解即可;
(2)用标准质量加上与标准质量的差值之和进行计算即可;
(3)先求出成本,根据按照全部销售后获得利润为成本的作为销售目标制定零售价,求出零售价,再根据两天的销售方式,求出总售价,利用总售价减去成本,进行判断即可.
【详解】(1)解:(千克)
答:这20箱樱桃质量相差最大是1.3千克.
(2)
(千克)
这20箱樱桃的总质量是205千克.
(3)
(元)
(元)
(元)
答:该水果店销售这批樱桃共盈利1312元
26.【答案】(1)4,
(2)
(3)的平方根为
【分析】(1)根据无理数的估算求解即可;
(2)根据无理数的估算求解即可;
(3)首先根据无理数的估算求出x和y的值,然后代入求解即可.
【详解】(1)∵
∴
∴的整数部分是4,小数部分是,
故答案为:4,;
(2)∵,
∴,,
∴.
(3)∵
∴
∴,,
∴,
.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
苏教版七年级上册数学 期中测试(1-4章) 单元测试
【浙教版】
学校:___________姓名:___________班级:___________考号:___________
满分:120分 考试时间:120分钟
题号 一 二 三 总分
得分
选择题(本大题共10小题,每小题3分,共30分。下列各题的备选答案中,只有一项是最符合题意的,请选出。)
1.的倒数是( )
A. B. C. D.
2.绝对值大于且小于的整数个数是( )
A. B. C. D.
3.若在单位长度的数轴上随意画出一条长的线段,则线段盖住的整数点至少有( )
A.9个 B.10个 C.100个 D.101个
4.若与是同一个数的两个不同的平方根,则m的值( )
A. B.1 C.或1 D.
5.若,则的值是( )
A.2 B.1 C. D.3
6.点A,B在数轴上的位置如图所示,其对应的有理数分别是a和b.对于下列四个结论:①;②;③;④;⑤.其中正确的是( )
A.①②③④ B.①②③⑤ C.①③⑤ D.②③④
7.某学校计划购买甲、乙两种品牌的电子白板共40台.甲、乙两种品牌电子白板的单价分别为2.5万元/台和1.5万元/台,若购买甲品牌电子白板费用为万元,则购买乙品牌电子白板费用为( )
A.万元 B.万元 C.万元 D.万元
8.如图,在一个正方形的内部放置大小不同的两个小正方形,其中较大的正方形的面积为11,较小的正方形的面积为4,中间重叠部分的面积为1,则图中三角形的面积为( )
A.11 B.10 C.6 D.5
9.为了求的值,可令,则,因此,所以,仿照以上推理计算出的值是( )
A. B. C. D.
10.若规定“!”是一种数学运算符号,且1!=1,2!=2×1=2,3!=3×2×1=6,4!=4×3×2×1=24, ,则的值为( )
A.9900 B.99! C. D.2
填空题(本大题共10小题,每小题4分,共40分。)
11.绝对值是 .
12.目前,我国基本医疗保险覆盖已超过13500000000人,数据13500000000用科学记数法可以表示为 .
13.已知三个有理数、、,其积是负数,则 .
14.在计算两位数的平方运算时,我们可以利用“竖式”方式进行快速运算,其步骤如图所示(图1,2,3),现有一个两位数,其十位数字为,在进行平方运算时,部分步骤如图4所示(为小于的正整数),则这个两位数是 (用含的代数式表达).
15.在一条可以折叠的数轴上,A和B表示的数分别是和6,点C为A、B之间一点(不与A、B重合),以点C为折点,将此数轴向右对折,且,则C点表示的数是 .
16.比较大小: (填“”“”“”).
17.在这四个数中,任取两个数相乘,所得的积最大是 ,所得的积最小是 .
18.已知的立方根是3,,则= .
19.如图1,周长为20的长方形纸片剪成①,②,③,④号正方形和⑤号长方形,并将它们按图2的方式放入周长为40的长方形中,则没有覆盖的阴影部分的周长为
20.已知,,则 .
三、解答题(本大题共6小题,前5小题每小题8分,第6小题10分,共50分。解答应写出文字说明、证明过程或演算步骤.)
21.计算:
(1);
(2);
(3);
(4).
22.如图,数轴的单位长度为1,点表示的数是.
(1)在数轴上标出原点,点表示的数是________;
(2)在数轴上表示出下列各数:,,,,并将这些数及点,表示的数用“”号连接起来.
23.为了节省材料,某水产养殖户利用水库的岸堤(岸堤足够长)为一边, 用围网在水库中围成了如图所示的①、②、③三块长方形区域,其中区域①的一边长为a米,区域③长方形的长为b米, 是其宽的4倍.
(1)宽的长度为 米,围成养殖场围网的总长度为 米;
(2)当、时,求围网的总长度.
24.已知的立方根是,的平方根是.
(1)求的值.
(2)求的平方根.
25.某水果店以每箱200元的价格从水果批发市场购进20箱樱桃.若以每箱净重10千克为标准,超过的千克数记为正数,不足的千克数记为负数,称重的记录如下表:
与标准质量的差值(单位:千克) 0
箱数 1 4 3 4 5 3
(1)这20箱樱桃质量相差最大是多少千克?
(2)这20箱樱桃的总质量是多少千克?
(3)水果店购进这批樱桃需要付运费100元,要把这些樱桃全部以零售的形式卖掉,并按照全部销售后获得利润为成本的作为销售目标制定零售价,若第一天水果店以该零售价售出了总质量的,第二天因害怕剩余的樱桃腐烂,决定降价把剩余的樱桃按原零售价的七折售完,请计算该水果店在销售这批樱桃的过程中共盈利或亏损多少元?(提示:成本=总进价+运费)
26.阅读下面的文字,解答问题∶大家知道是无理数,而无理数是无限不循环小数,因此的小数部分我们不可能全部写出来.将这个数减去其整数部分,得到的差就是小数部分,因为的整数部分是1,于是用来表示的小数部分.又例如:
∵,即,
∴的整数部分是2,小数部分为.
根据上述材料,回答下列问题:
(1)的整数部分是___,小数部分是___.
(2)也是夹在相邻两个整数之间的,可以表示为,求的值;
(3)若的整数部分为x,小数部分为y,求的平方根.
参考答案
选择题
1.【答案】C
【分析】乘积为“1”的两个数互为倒数,根据定义解答即可.
【详解】解:∵,
∴的倒数是,
故选:C.
2.【答案】C
【分析】根据绝对值的定义解答即可.
【详解】解:绝对值大于且小于的所有整数是:,,共个.
故选:C.
3.【答案】C
【分析】分类讨论:线段的两端点是整数点,线段的两端点不是整数点,根据线段的长度,可得答案.
【详解】解:当线段的两端点是整数点时,一条长的线段,则被线段盖住的整数有个,
当线段的两端点不是整数点时,一条长的线段,则被线段盖住的整数有个,
线段盖住的整数点至少有个
故选:C.
4.【答案】B
【分析】根据一个正数的两个平方根互为相反数得到,即可求出m的值.
【详解】解:∵与是同一个数的两个不同的平方根,
∴,
∴,
故答案为:1.
5.【答案】C
【分析】原式变形后,将的值代入计算即可求出值.
【详解】解:∵,
∴原式,
故选:C.
6.【答案】B
【分析】由数轴可知:,据此即可求解.
【详解】解:由数轴可知:
①,故①正确;
②,∴,故②正确;
③,故③正确;
④,故④错误;
⑤,故⑤正确
故选:B
7.【答案】A
【分析】根据购买甲品牌电子白板费用为万元可得购买甲品牌电子白板台,可求出购买乙品牌电子白板的数量为台,再根据“单价×数量”可得结论.
【详解】解:∵甲品牌电子白板的单价分别为2.5万元/台,且购买甲品牌电子白板费用为万元,
∴购买甲品牌电子白板台,
∴购买乙品牌电子白板的数量为台,
∴购买乙品牌电子白板费用为万元
故选:A
8.【答案】D
【分析】观察图形可知,两个空白部分的长相等,宽也相等,则重叠部分也为正方形,根据较大的正方形的面积为11,较小的正方形的面积为4,中间重叠部分的面积为1,则较大的正方形的边长为,较小的正方形的边长为2,中间重叠部分的正方形边长为1;从而得出空白部分的长方形的较小边长为,继而得,,然后由求解即可.
【详解】解:观察图形可知,两个空白部分的长相等,宽也相等,
重叠部分也为正方形,
∵较大的正方形的面积为11,较小的正方形的面积为4,中间重叠部分的面积为1,
∴较大的正方形的边长为,较小的正方形的边长为2,中间重叠部分的正方形边长为1;
∴空白部分的长方形的较小边长为,
∴
∴
∴
故选:D.
9.【答案】D
【分析】本题通过题干给出的方法,可以设,然后用,得到M的解.
【详解】解:设 ,
故选:D.
10.【答案】A
【分析】先根据数学运算符号“!”得出和的值,再计算有理数的乘除法即可得.
【详解】由题意得:
故选:A.
填空题
11.【答案】
【分析】根据绝对值的意义解答即可.
【详解】解:负数的绝对值是它的相反数,
的绝对值是,
故答案为:.
12.【答案】
【分析】科学记数法的表示形式为的形式,其中,为整数.确定的值时,要看把原数变成时,小数点移动了多少位,的绝对值与小数点移动的位数相同.当原数绝对值时,是正整数;当原数的绝对值时,是负整数.
【详解】解:,
故答案为:.
13.【答案】或
【分析】根据题意可知,有两种情况:①、、均为负数;②、、中有一个负数,根据绝对值的意义化简求值,即可得到答案
【详解】解:由题意可知,,则有两种情况:
①、、均为负数,则
②、、中有一个负数,则,
故答案为:或
14.【答案】
【分析】观察图形可发现:“竖式”的第一行从左向右分别为:十位上的数字的平方与个位上的数字的平方,即中的是中的平方,中的是中的平方,每个数的平方占两个空,平方是一位数的前面的空用填补;第二行从左向右是这个两位数的个位上的数字与十位上的数字之积的倍,即是中,乘积为两位的填中间两个空格,乘积为三位数的从左边第一个空格开始填.以此规律即可解答.
【详解】解:根据题意可得,图1,竖式中第一行:中的是中的平方,中的是中的平方;第二行:是中;
图2,竖式中第一行:中的是中的平方,中的是中的平方;第二行:是中;
图3,竖式中第一行:中的是中的平方,中的是中的平方;第二行:是中;
∴图4中,第二行的这个两位数可表示为:,这个数是某个乘方数中十位上的数字与个位上的数字之积的倍,
∴这个两位数的十位上的数字与个位上的数字之积为:,
∵这个两位数的十位数字为,
∴这个两位数的个位数字为,
∴这个两位数是,
故答案为:.
15.【答案】或
【分析】设点C表示的数为x,根据点A表示的数为,点B表示的数为6,得到,,根据,或,且, 分类讨论即得.
【详解】设点C表示的数为x,
∵点A表示的数为,点B表示的数为6,
∴,,
∵,
∴,,
或,.
故答案为:或.
16.【答案】
【分析】按照两个负数比较大小的法则进行比较即可.
【详解】解:,
.
故答案为:.
17.【答案】 24
【分析】根据两数相乘,同号得正、异号得负求两数的积,再由正数大于负数,即可求解.
【详解】解:∵,
∴积最大是24,
∵,
∴积最小是,
故答案为:24,.
18.【答案】1或3/3或1
【分析】根据题意求出,的值,代入即可求解.
【详解】解:的立方根是3,
,
,
,
,
当,时,
;
当,时,
;
综上,的值为1或3,
故答案为:1或3.
19.【答案】30
【分析】在图1中,设①号正方形的边长为x,②号正方形的边长为y,则③号正方形的边长为,④号正方形的边长为,根据图1的周长求得,再根据图2的周长求得,进而可由没有覆盖的阴影部分的周长为求解即可.
【详解】解:在图1中,设①号正方形的边长为x,②号正方形的边长为y,则③号正方形的边长为,④号正方形的边长为,
由图1中长方形的周长为20得,
解得:,
如图2,
由图2中的长方形的周长为40得,
∴,
由图2得没有覆盖的阴影部分的周长为,
故答案为:30.
20.【答案】
【分析】将两边同时平方可得出,由可得出,从而即可得到答案.
【详解】解:,
,
,
,
,
,
,
故答案为:.
解答题
21.【答案】(1)
(2)
(3)
(4)3
【详解】(1)
;
(2)
;
(3)
;
(4)
.
22.【答案】(1)4
(2)见解析,
【分析】(1)根据的相对位置即可求解;
(2)先将各数化简,即可求解.
【详解】(1)解:∵点在点的右边,且距离点个单位长度
故点表示的数是:
故答案为:
(2)解:
在数轴上表示各数,如图所示:
由数轴可知:
23.【答案】(1);
(2)240
【分析】(1)根据图示得出的长,进而得出养殖场围网的总长度;
(2)把、代入代数式解答即可.
【详解】(1)解:∵长方形的长为b米, 是其宽的4倍.
∴,
∵为a米,
∴围成养殖场围网的总长度(米);
(2)把,代入(米),
答:围网的总长度为240米.
24.【答案】(1),
(2)
【分析】(1)根据平方根、立方根的定义可得,求解即可;
(2)将的值代入,然后根据平方根的定义求解即可.
【详解】(1)解:∵的立方根是,的平方根是.
∴,
解得:,;
(2)解:∵,,
∴,
∵的平方根是,
∴的平方根.
26.【答案】(1)这20箱樱桃质量相差最大是1.3千克
(2)这20箱樱桃的总质量是205千克
(3)该水果店销售这批樱桃共盈利1312元
【分析】(1)用与标准质量的差值中的最大值减去最小值进行求解即可;
(2)用标准质量加上与标准质量的差值之和进行计算即可;
(3)先求出成本,根据按照全部销售后获得利润为成本的作为销售目标制定零售价,求出零售价,再根据两天的销售方式,求出总售价,利用总售价减去成本,进行判断即可.
【详解】(1)解:(千克)
答:这20箱樱桃质量相差最大是1.3千克.
(2)
(千克)
这20箱樱桃的总质量是205千克.
(3)
(元)
(元)
(元)
答:该水果店销售这批樱桃共盈利1312元
26.【答案】(1)4,
(2)
(3)的平方根为
【分析】(1)根据无理数的估算求解即可;
(2)根据无理数的估算求解即可;
(3)首先根据无理数的估算求出x和y的值,然后代入求解即可.
【详解】(1)∵
∴
∴的整数部分是4,小数部分是,
故答案为:4,;
(2)∵,
∴,,
∴.
(3)∵
∴
∴,,
∴,
.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
