第一章综合测试题(含答案)
图片预览



文档简介
中小学教育资源及组卷应用平台
第一章综合测试题
时间: 45分钟 满分: 100分 得 分:__________
一、选择题(每题3分,共30分)
1.在△ABC中,∠A=36°,∠B=72°,则△ABC是 ( )
A.钝角三角形 B.等腰三角形 C.等边三角形 D.等腰直角三角形
2.下列长度的3 根小木棒不能搭成三角形的是 ( )
3.如图,在△ABC 中,∠C=90°,点D在AC上,DE∥AB,若∠CDE=160°,则∠B的度数为 ( )
A.40° B.50° C.60° D.70°
第3题图 第4题图
4.如图,点 D,E分别在线段AB,AC上,CD 与BE 相交于O点,已知AB=AC,添加下列条件,不能证明△ABE≌△ACD的是 ( )
A.∠B=∠C B. BE=CD C. BD=CE D.∠BDO=∠CEO
5.如图所示,将含 45°角的直角三角板与含角的直角三角板叠放在一起,若∠1=70°,则∠2的度数为( )
A.85° B.60° C.50°
6.中国古代数学家刘徽在《九章算术注》中,给出了证明三角形面积公式的出入相补法.如图,在△ABC 中,分别取AB,AC的中点D,E,连接DE,过点 A 作AF⊥DE,垂足为 F,将△ABC分割后拼接成长方形 BCHG.若DE=5,AF=3,则△ABC的面积是 ( )
A.20 B.25 C.30 D.35
7.如图,图1中有3个以MN为高的三角形,图2中有10个以MN为高的三角形,图3 中有21个以MN为高的三角形,…,以此类推,则图6中以MN为高的三角形的个数为 ( )
A.55 B.78 C.96 D.105
8.如图,在△ABC和△BDE中,点C在边BD上,边AC交边BE于点F,若 AC=BD,AB=ED,BC=BE,则∠ACB等于( )
A.∠EDB B.∠BED C.∠EBD D.2∠ABF
第8题图 第9题图
9.如图,四边形 ABCD 是正方形,BE⊥EF,DF⊥EF,BE=2.5cm ,DF=4 cm,那么 EF 的长为 ( )
A.6.5 cm B.6 cm C.5.5 cm D.4 cm
10.如图,把△ABC沿DE 折叠,当点 A 落在四边形 BCDE 内部时,则∠A 与∠1+∠2 之间有一种数量关系始终保持不变,请试着找一找这个规律,你发现的规律是 ( )
二、填空题(每题4分,共24分)
11.如图,已知 连接AB,∠ABE = 65°,∠BAD = 30°,则∠CBE 的度数为
______________.
12. 如图,已知∠ABC=∠DCB,添加下列条件中的一个:①∠A=∠D ②AC=DB ③AB=DC.其中不能确定的是_____________.(填序号)
第12题图 第13题图
13.如图,点O是,的三条中线AD,BE,CF的交点,若阴影部分的面积 则 的面积为_____________.
14.在 中, AD 是的中线,设AD长为m,则m的取值范围是___________.
第4题图 第15题图
15.如图,在 中, 垂足分别是点 D,E,AD,CE 交于点 H,已知 则 __________.
16.当三角形中一个内角β是另外一个内角α的0.5倍时,我们称此三角形为“友好三角形”,其中α是这个“友好三角形”的“友好角”.如果一个“友好三角形”中有一个内角为54°,那么这个“友好三角形”的“友好角”的度数为____________.
三、解答题(共46分)
17.(8分)已知:线段 a,∠α,求作: 使 ∠B=∠α.
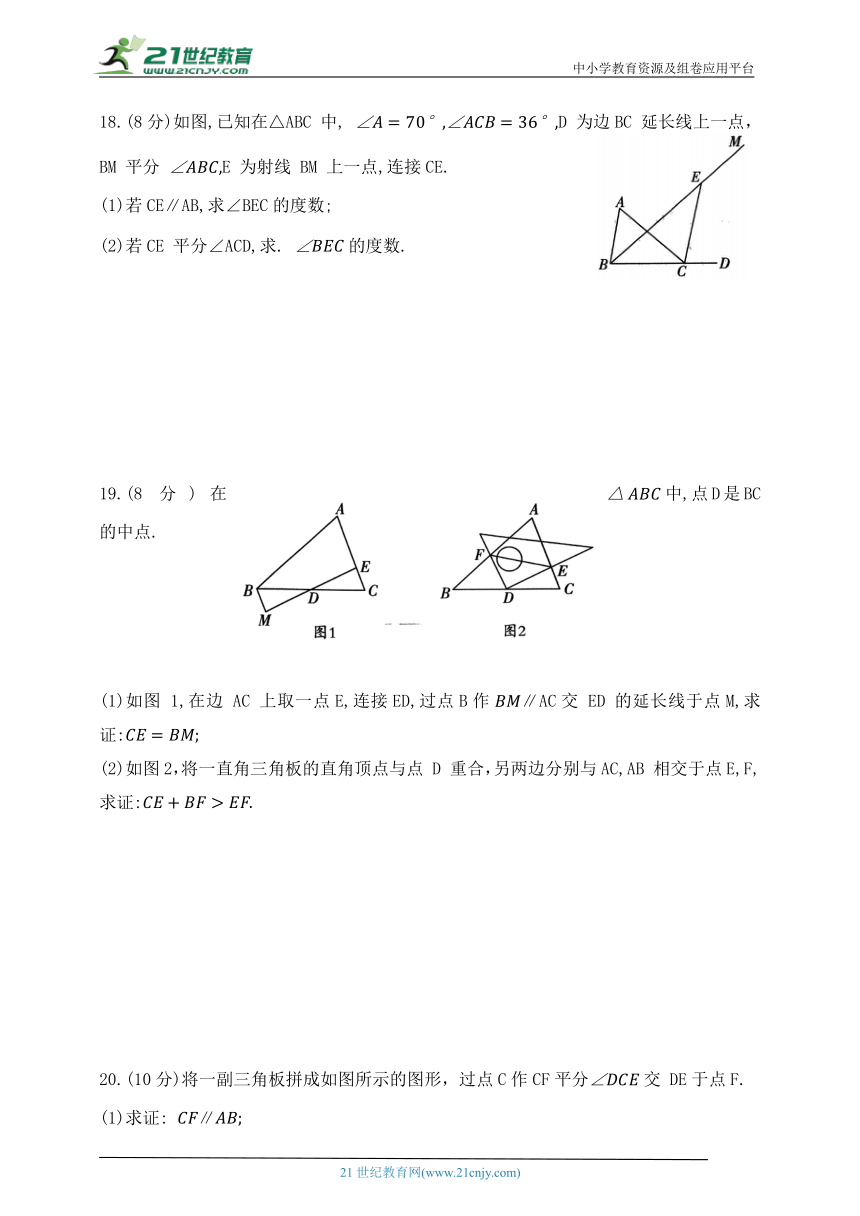
18.(8分)如图,已知在△ABC 中, D 为边BC 延长线上一点,BM 平分 E 为射线 BM 上一点,连接CE.
(1)若CE∥AB,求∠BEC的度数;
(2)若CE 平分∠ACD,求. 的度数.
19.(8分)在中,点D是BC的中点.
(1)如图 1,在边 AC 上取一点E,连接ED,过点B作∥AC交 ED 的延长线于点M,求证:
(2)如图2,将一直角三角板的直角顶点与点 D 重合,另两边分别与AC,AB 相交于点E,F,求证:
20.(10分)将一副三角板拼成如图所示的图形,过点C作CF平分交 DE于点F.
(1)求证: ∥
(2)求 的度数.
21.(12分)“一线三等角”模型是平面几何图形中的重要模型之一,“一线三等角”指的是图形中出现同一条直线上有3个角相等的情况,在学习过程中,我们发现“一线三等角”模型的出现,还经常会伴随着出现全等三角形.根据对材料的理解解决以下问题:
(1)如图 1, 猜想DE,AD,BE之间的关系;
(2)如图2,将(1)中条件改为. 请问(1)中的结论是否成立 若成立,请给出证明;若不成立,请说明理由;
(3)如图3,在中,点D为AB上一点,,请直接写出AB的长.
参考答案
1. B 2. B 3. D 4. B 5. D 6. C
7.B 解析:图1 中以 MN为高的三角形的个数是 图 2 中以 MN 为高的三角形的个数是 图 3 中以MN为高的三角形的个数是 图 6 中以MN为高的三角形的个数是
8. C 9. A 10. B
12. ② 13. 6
解析:如图所示,延长 AD 至点 E,使 连接 EC.
因为 AD,∠ADB=∠EDC,所以△ABD≌△ECD(SAS),所以CE=AB=5.
15.4
16.54°或108°或84°
解析:①当三角形中一个内角α=54°时,“友好角”的度数为54°;
②当三角形中一个内角β=54°时,由题意得α=54°÷0.5=108°,
所以“友好角”的度数为 108°;
③当54°角既不是α也不是β时,
因为α+β+54°=180°,所以
所以α=84°,所以“友好角”的度数为84°.
17.解:如图所示,△ABC即为所求作.
18.解:(1)因为∠A=70°,∠ACB=36°,
所以∠ABC=180°-∠A-∠ACB=180°-70°-36°=74°.
因为 BM平分∠ABC,所以
因为CE∥AB,所以∠BEC=∠ABE=37°;
(2)因为∠ACB=36°,所以∠ACD=180°-∠ACB=180°-36°=144°.
因为 BM 平分∠ABC, CE 平分∠ACD,∠ABC=74°,
所以
所以∠BCE = 180°-∠ECD=180°-72°=108°,
所以∠BEC=180°-∠EBC-∠BCE=180°-37°-108°=35°.
19.解:(1)证明:因为点 D 是 BC 的中点,所以 BD=CD.
因为 BM∥AC,所以∠CED=∠M,∠C=∠DBM,
所以△EDC≌△MDB(AAS),所以CE=BM;
(2)如图,过点 B 作 BM∥AC 交 ED 延长线于点 M,连接 MF.
20.解:(1)证明:由题意,得△ACB是等腰直角三角形,且∠ACB=∠DCE=90°,
所以∠B=45°.
因为CF平分∠DCE,所以∠DCF=∠ECF=45°,
所以∠B=∠ECF,所以 CF∥AB;
(2)由三角板知,∠E=60°,由(1)知,∠ECF=45°,
所以∠CFE=180°-60°-45°=75°,所以∠DFC=180°-75°=105°.
21.解:(1)DE=AD+BE.理由:
因为∠ADC=∠CEB=∠ACB=90°,所以∠ACD+∠CAD=∠ACD+∠BCE=90°,
所以∠CAD=∠BCE,
又因为 AC=BC,所以△ADC≌△CEB(AAS),
所以CE=AD,CD=BE,所以DE=CD+CE=BE+AD;
(2)(1)中结论仍然成立,理由:
因为∠ADC=∠CEB=∠ACB,∠BCE+∠ACD=180°-∠ACB,∠ACD+∠CAD=180°-∠ADC,
所以∠CAD=∠BCE.
在△ADC 和△CEB中, 所以△ADC≌△CEB(AAS),
所以AD=CE,DC=BE,所以 DE=AD+BE,
所以(1)中结论仍然成立;
(3) 因为∠A = ∠EDF =∠B,∠EDB =180°-∠ADE=∠A+∠AED=∠EDF+∠FDB,
所以∠AED=∠FDB,
因为 DE=DF,所以△AED≌△BDF(AAS),所以AE=BD,AD=BF,
所以AB=AD+BD=AE+BF=2+5=7.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第一章综合测试题
时间: 45分钟 满分: 100分 得 分:__________
一、选择题(每题3分,共30分)
1.在△ABC中,∠A=36°,∠B=72°,则△ABC是 ( )
A.钝角三角形 B.等腰三角形 C.等边三角形 D.等腰直角三角形
2.下列长度的3 根小木棒不能搭成三角形的是 ( )
3.如图,在△ABC 中,∠C=90°,点D在AC上,DE∥AB,若∠CDE=160°,则∠B的度数为 ( )
A.40° B.50° C.60° D.70°
第3题图 第4题图
4.如图,点 D,E分别在线段AB,AC上,CD 与BE 相交于O点,已知AB=AC,添加下列条件,不能证明△ABE≌△ACD的是 ( )
A.∠B=∠C B. BE=CD C. BD=CE D.∠BDO=∠CEO
5.如图所示,将含 45°角的直角三角板与含角的直角三角板叠放在一起,若∠1=70°,则∠2的度数为( )
A.85° B.60° C.50°
6.中国古代数学家刘徽在《九章算术注》中,给出了证明三角形面积公式的出入相补法.如图,在△ABC 中,分别取AB,AC的中点D,E,连接DE,过点 A 作AF⊥DE,垂足为 F,将△ABC分割后拼接成长方形 BCHG.若DE=5,AF=3,则△ABC的面积是 ( )
A.20 B.25 C.30 D.35
7.如图,图1中有3个以MN为高的三角形,图2中有10个以MN为高的三角形,图3 中有21个以MN为高的三角形,…,以此类推,则图6中以MN为高的三角形的个数为 ( )
A.55 B.78 C.96 D.105
8.如图,在△ABC和△BDE中,点C在边BD上,边AC交边BE于点F,若 AC=BD,AB=ED,BC=BE,则∠ACB等于( )
A.∠EDB B.∠BED C.∠EBD D.2∠ABF
第8题图 第9题图
9.如图,四边形 ABCD 是正方形,BE⊥EF,DF⊥EF,BE=2.5cm ,DF=4 cm,那么 EF 的长为 ( )
A.6.5 cm B.6 cm C.5.5 cm D.4 cm
10.如图,把△ABC沿DE 折叠,当点 A 落在四边形 BCDE 内部时,则∠A 与∠1+∠2 之间有一种数量关系始终保持不变,请试着找一找这个规律,你发现的规律是 ( )
二、填空题(每题4分,共24分)
11.如图,已知 连接AB,∠ABE = 65°,∠BAD = 30°,则∠CBE 的度数为
______________.
12. 如图,已知∠ABC=∠DCB,添加下列条件中的一个:①∠A=∠D ②AC=DB ③AB=DC.其中不能确定的是_____________.(填序号)
第12题图 第13题图
13.如图,点O是,的三条中线AD,BE,CF的交点,若阴影部分的面积 则 的面积为_____________.
14.在 中, AD 是的中线,设AD长为m,则m的取值范围是___________.
第4题图 第15题图
15.如图,在 中, 垂足分别是点 D,E,AD,CE 交于点 H,已知 则 __________.
16.当三角形中一个内角β是另外一个内角α的0.5倍时,我们称此三角形为“友好三角形”,其中α是这个“友好三角形”的“友好角”.如果一个“友好三角形”中有一个内角为54°,那么这个“友好三角形”的“友好角”的度数为____________.
三、解答题(共46分)
17.(8分)已知:线段 a,∠α,求作: 使 ∠B=∠α.
18.(8分)如图,已知在△ABC 中, D 为边BC 延长线上一点,BM 平分 E 为射线 BM 上一点,连接CE.
(1)若CE∥AB,求∠BEC的度数;
(2)若CE 平分∠ACD,求. 的度数.
19.(8分)在中,点D是BC的中点.
(1)如图 1,在边 AC 上取一点E,连接ED,过点B作∥AC交 ED 的延长线于点M,求证:
(2)如图2,将一直角三角板的直角顶点与点 D 重合,另两边分别与AC,AB 相交于点E,F,求证:
20.(10分)将一副三角板拼成如图所示的图形,过点C作CF平分交 DE于点F.
(1)求证: ∥
(2)求 的度数.
21.(12分)“一线三等角”模型是平面几何图形中的重要模型之一,“一线三等角”指的是图形中出现同一条直线上有3个角相等的情况,在学习过程中,我们发现“一线三等角”模型的出现,还经常会伴随着出现全等三角形.根据对材料的理解解决以下问题:
(1)如图 1, 猜想DE,AD,BE之间的关系;
(2)如图2,将(1)中条件改为. 请问(1)中的结论是否成立 若成立,请给出证明;若不成立,请说明理由;
(3)如图3,在中,点D为AB上一点,,请直接写出AB的长.
参考答案
1. B 2. B 3. D 4. B 5. D 6. C
7.B 解析:图1 中以 MN为高的三角形的个数是 图 2 中以 MN 为高的三角形的个数是 图 3 中以MN为高的三角形的个数是 图 6 中以MN为高的三角形的个数是
8. C 9. A 10. B
12. ② 13. 6
解析:如图所示,延长 AD 至点 E,使 连接 EC.
因为 AD,∠ADB=∠EDC,所以△ABD≌△ECD(SAS),所以CE=AB=5.
15.4
16.54°或108°或84°
解析:①当三角形中一个内角α=54°时,“友好角”的度数为54°;
②当三角形中一个内角β=54°时,由题意得α=54°÷0.5=108°,
所以“友好角”的度数为 108°;
③当54°角既不是α也不是β时,
因为α+β+54°=180°,所以
所以α=84°,所以“友好角”的度数为84°.
17.解:如图所示,△ABC即为所求作.
18.解:(1)因为∠A=70°,∠ACB=36°,
所以∠ABC=180°-∠A-∠ACB=180°-70°-36°=74°.
因为 BM平分∠ABC,所以
因为CE∥AB,所以∠BEC=∠ABE=37°;
(2)因为∠ACB=36°,所以∠ACD=180°-∠ACB=180°-36°=144°.
因为 BM 平分∠ABC, CE 平分∠ACD,∠ABC=74°,
所以
所以∠BCE = 180°-∠ECD=180°-72°=108°,
所以∠BEC=180°-∠EBC-∠BCE=180°-37°-108°=35°.
19.解:(1)证明:因为点 D 是 BC 的中点,所以 BD=CD.
因为 BM∥AC,所以∠CED=∠M,∠C=∠DBM,
所以△EDC≌△MDB(AAS),所以CE=BM;
(2)如图,过点 B 作 BM∥AC 交 ED 延长线于点 M,连接 MF.
20.解:(1)证明:由题意,得△ACB是等腰直角三角形,且∠ACB=∠DCE=90°,
所以∠B=45°.
因为CF平分∠DCE,所以∠DCF=∠ECF=45°,
所以∠B=∠ECF,所以 CF∥AB;
(2)由三角板知,∠E=60°,由(1)知,∠ECF=45°,
所以∠CFE=180°-60°-45°=75°,所以∠DFC=180°-75°=105°.
21.解:(1)DE=AD+BE.理由:
因为∠ADC=∠CEB=∠ACB=90°,所以∠ACD+∠CAD=∠ACD+∠BCE=90°,
所以∠CAD=∠BCE,
又因为 AC=BC,所以△ADC≌△CEB(AAS),
所以CE=AD,CD=BE,所以DE=CD+CE=BE+AD;
(2)(1)中结论仍然成立,理由:
因为∠ADC=∠CEB=∠ACB,∠BCE+∠ACD=180°-∠ACB,∠ACD+∠CAD=180°-∠ADC,
所以∠CAD=∠BCE.
在△ADC 和△CEB中, 所以△ADC≌△CEB(AAS),
所以AD=CE,DC=BE,所以 DE=AD+BE,
所以(1)中结论仍然成立;
(3) 因为∠A = ∠EDF =∠B,∠EDB =180°-∠ADE=∠A+∠AED=∠EDF+∠FDB,
所以∠AED=∠FDB,
因为 DE=DF,所以△AED≌△BDF(AAS),所以AE=BD,AD=BF,
所以AB=AD+BD=AE+BF=2+5=7.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
