第一章 三角形 5 利用三角形全等测距离(含答案)
文档属性
| 名称 | 第一章 三角形 5 利用三角形全等测距离(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 5.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-25 13:41:41 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第一章 三角形
5 利用三角形全等测距离
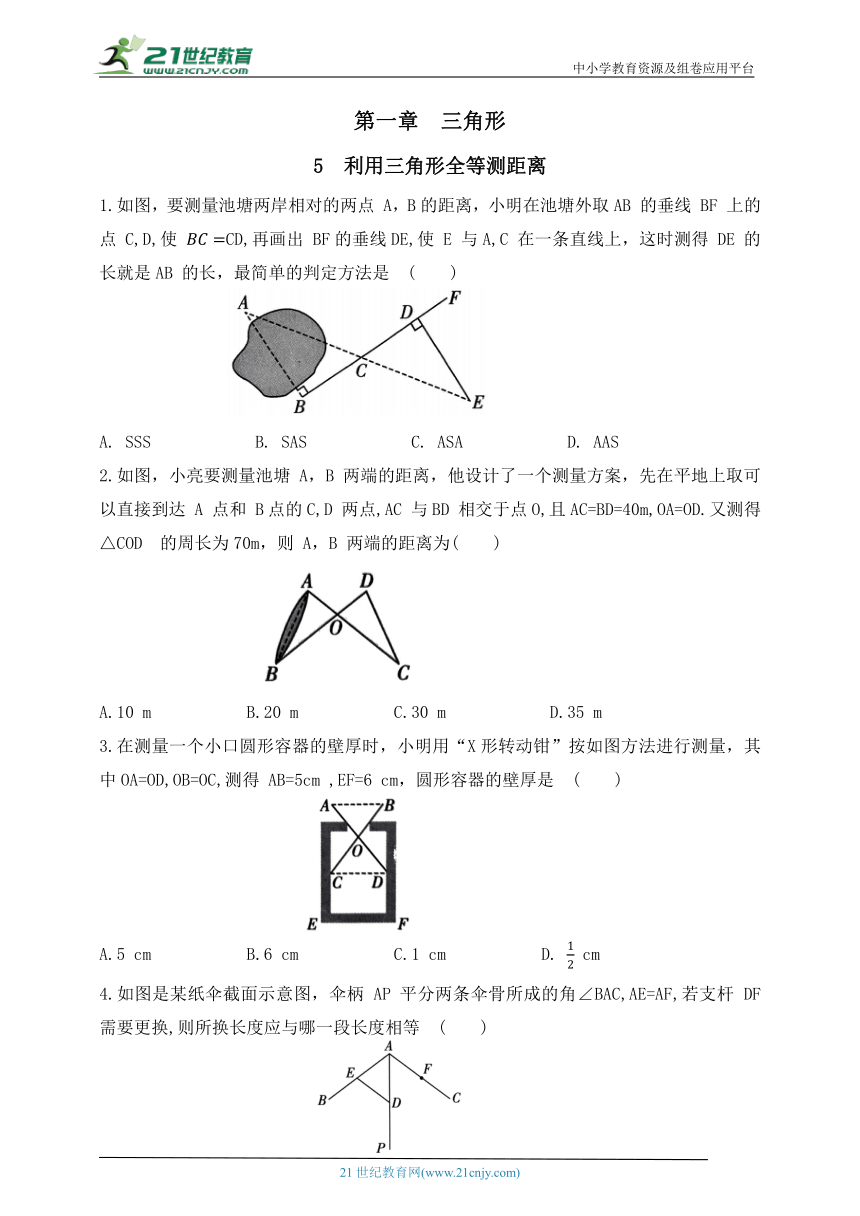
1.如图,要测量池塘两岸相对的两点 A,B的距离,小明在池塘外取AB 的垂线 BF 上的点 C,D,使 CD,再画出 BF的垂线DE,使 E 与A,C 在一条直线上,这时测得 DE 的长就是AB 的长,最简单的判定方法是 ( )
A. SSS B. SAS C. ASA D. AAS
2.如图,小亮要测量池塘 A,B 两端的距离,他设计了一个测量方案,先在平地上取可以直接到达 A 点和 B点的C,D 两点,AC 与BD 相交于点O,且AC=BD=40m,OA=OD.又测得△COD 的周长为70m,则 A,B 两端的距离为( )
A.10 m B.20 m C.30 m D.35 m
3.在测量一个小口圆形容器的壁厚时,小明用“X形转动钳”按如图方法进行测量,其中OA=OD,OB=OC,测得 AB=5cm ,EF=6 cm,圆形容器的壁厚是 ( )
A.5 cm B.6 cm C.1 cm D. cm
4.如图是某纸伞截面示意图,伞柄 AP 平分两条伞骨所成的角∠BAC,AE=AF,若支杆 DF 需要更换,则所换长度应与哪一段长度相等 ( )
A. BE B. AE C. DE D. DP
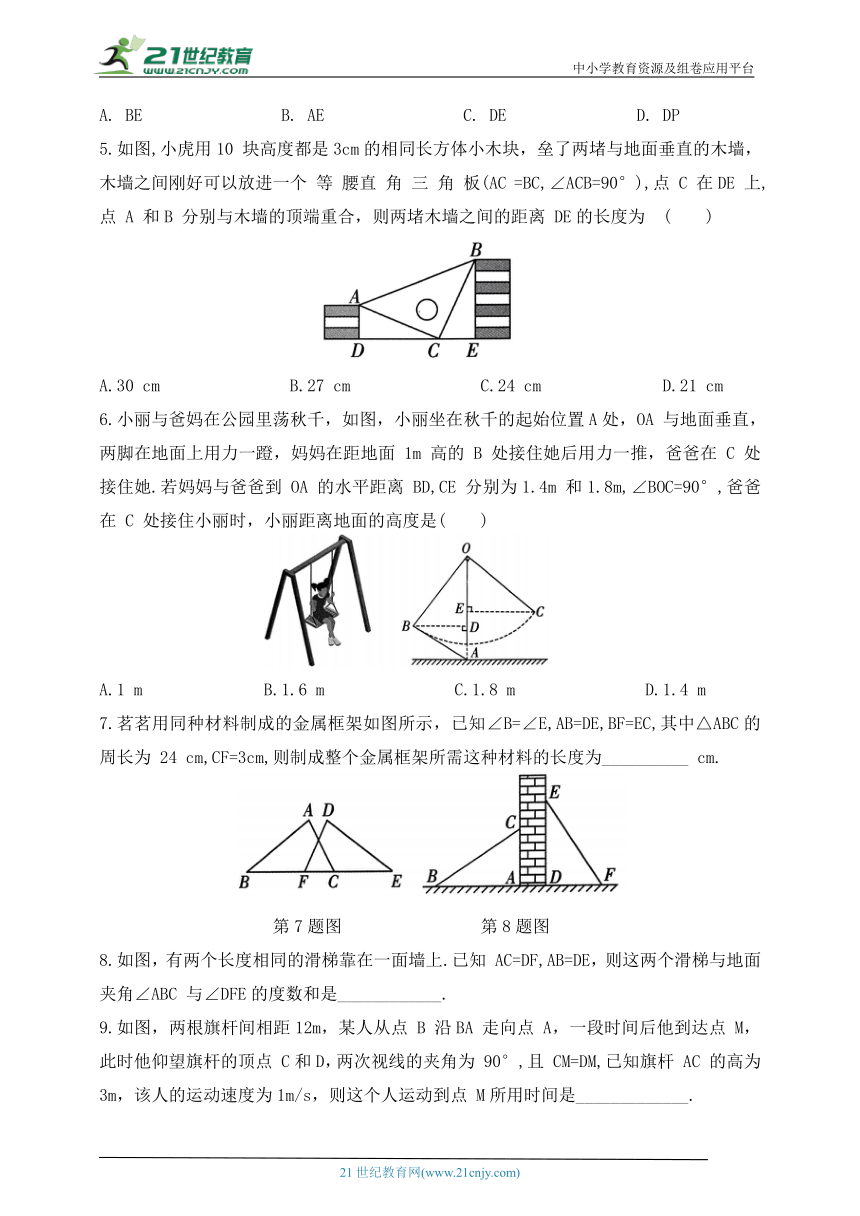
5.如图,小虎用10 块高度都是3cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个 等 腰直 角 三 角 板(AC =BC,∠ACB=90°),点 C 在DE 上,点 A 和B 分别与木墙的顶端重合,则两堵木墙之间的距离 DE的长度为 ( )
A.30 cm B.27 cm C.24 cm D.21 cm
6.小丽与爸妈在公园里荡秋千,如图,小丽坐在秋千的起始位置A处,OA 与地面垂直,两脚在地面上用力一蹬,妈妈在距地面 1m 高的 B 处接住她后用力一推,爸爸在 C 处接住她.若妈妈与爸爸到 OA 的水平距离 BD,CE 分别为1.4m 和1.8m,∠BOC=90°,爸爸在 C 处接住小丽时,小丽距离地面的高度是( )
A.1 m B.1.6 m C.1.8 m D.1.4 m
7.茗茗用同种材料制成的金属框架如图所示,已知∠B=∠E,AB=DE,BF=EC,其中△ABC的周长为 24 cm,CF=3cm,则制成整个金属框架所需这种材料的长度为__________ cm.
第7题图 第8题图
8.如图,有两个长度相同的滑梯靠在一面墙上.已知 AC=DF,AB=DE,则这两个滑梯与地面夹角∠ABC 与∠DFE的度数和是____________.
9.如图,两根旗杆间相距12m,某人从点 B 沿BA 走向点 A,一段时间后他到达点 M,此时他仰望旗杆的顶点 C和D,两次视线的夹角为 90°,且 CM=DM,已知旗杆 AC 的高为3m,该人的运动速度为1m/s,则这个人运动到点 M所用时间是_____________.
第9题图 第10题图
10.如图,小明与小红玩跷跷板游戏,如果跷跷板的支点 O(即跷跷板的中点)至地面的距离是50cm,当小红从水平位置 CD下降 30cm时,这时小明离地面的高度是________cm.
11.教室里有几盆花,如图1,测量这几盆花两旁的A,B 两点间的距离不方便,因此,选点A,B 都能到达的一点O,如图 2,连接BO并延长BO 到点C,使 CO=BO,连接AO并延长AO 到点 D,使 DO=AO.那么C,D两点间的距离就是A,B 两点间的距离.请说明理由.
12.如图,要测量河两岸上A,B 两点的距离,在点 B所在河岸一侧平地上取一点 C,使A,B,C在一条直线上,另取点 D,使 CD=BC,测得∠DCB=100°,∠ADC=65°,在CD的延长线上取点E,使 这时测得 DE的长就是A,B 两点的距离,为什么
13.如图所示,O为码头,A,B 两个灯塔与码头的距离相等,OA,OB为海岸线,一轮船从码头开出,计划沿 的平分线航行,航行途中,测得轮船与灯塔A,B的距离相
等,此时轮船有没有偏离航线 画出图形并说明你的理由.
参考答案
1. C 2. C 3. D 4. C 5. A
6.D 解析:由题意可知 OB=OC,
因为 所以90°,
所以,
在△COE 和△OBD中, 所以△COE≌△OBD(AAS),
所以CE=OD,OE=BD.
因为 BD,CE分别为 1.4m 和1.8m,所以DE=OD-OE=CE-BD=1.8-1.4=0.4(m),
因为 AD=1m,所以AE=AD+DE=1.4(m),
所以爸爸是在距离地面1.4m 的地方接住小丽的.
7.45 8.90° 9.3s 10.80
11.解:在△COD和△BOA 中,CO=BO,∠COD=∠BOA,DO=AO,所以△COD≌△BOA(SAS).
所以CD=AB.所以只要测出C,D两点间的距离就可知A,B两点间的距离.
12.证明:因为∠DCB=100°,∠ADC=65°,所以∠A=15°,所以∠BEC=∠A.
在△BCE和△DCA中, 所以△BCE≌△DCA(AAS),
所以AC=CE,
因为 所以 即
所以测得 DE的长就是A,B两点的距离.
13.解:此时轮船没有偏离航线.理由:
如图,由题意知( PB,所以
所以 所以此时轮船没有偏离航线.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第一章 三角形
5 利用三角形全等测距离
1.如图,要测量池塘两岸相对的两点 A,B的距离,小明在池塘外取AB 的垂线 BF 上的点 C,D,使 CD,再画出 BF的垂线DE,使 E 与A,C 在一条直线上,这时测得 DE 的长就是AB 的长,最简单的判定方法是 ( )
A. SSS B. SAS C. ASA D. AAS
2.如图,小亮要测量池塘 A,B 两端的距离,他设计了一个测量方案,先在平地上取可以直接到达 A 点和 B点的C,D 两点,AC 与BD 相交于点O,且AC=BD=40m,OA=OD.又测得△COD 的周长为70m,则 A,B 两端的距离为( )
A.10 m B.20 m C.30 m D.35 m
3.在测量一个小口圆形容器的壁厚时,小明用“X形转动钳”按如图方法进行测量,其中OA=OD,OB=OC,测得 AB=5cm ,EF=6 cm,圆形容器的壁厚是 ( )
A.5 cm B.6 cm C.1 cm D. cm
4.如图是某纸伞截面示意图,伞柄 AP 平分两条伞骨所成的角∠BAC,AE=AF,若支杆 DF 需要更换,则所换长度应与哪一段长度相等 ( )
A. BE B. AE C. DE D. DP
5.如图,小虎用10 块高度都是3cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个 等 腰直 角 三 角 板(AC =BC,∠ACB=90°),点 C 在DE 上,点 A 和B 分别与木墙的顶端重合,则两堵木墙之间的距离 DE的长度为 ( )
A.30 cm B.27 cm C.24 cm D.21 cm
6.小丽与爸妈在公园里荡秋千,如图,小丽坐在秋千的起始位置A处,OA 与地面垂直,两脚在地面上用力一蹬,妈妈在距地面 1m 高的 B 处接住她后用力一推,爸爸在 C 处接住她.若妈妈与爸爸到 OA 的水平距离 BD,CE 分别为1.4m 和1.8m,∠BOC=90°,爸爸在 C 处接住小丽时,小丽距离地面的高度是( )
A.1 m B.1.6 m C.1.8 m D.1.4 m
7.茗茗用同种材料制成的金属框架如图所示,已知∠B=∠E,AB=DE,BF=EC,其中△ABC的周长为 24 cm,CF=3cm,则制成整个金属框架所需这种材料的长度为__________ cm.
第7题图 第8题图
8.如图,有两个长度相同的滑梯靠在一面墙上.已知 AC=DF,AB=DE,则这两个滑梯与地面夹角∠ABC 与∠DFE的度数和是____________.
9.如图,两根旗杆间相距12m,某人从点 B 沿BA 走向点 A,一段时间后他到达点 M,此时他仰望旗杆的顶点 C和D,两次视线的夹角为 90°,且 CM=DM,已知旗杆 AC 的高为3m,该人的运动速度为1m/s,则这个人运动到点 M所用时间是_____________.
第9题图 第10题图
10.如图,小明与小红玩跷跷板游戏,如果跷跷板的支点 O(即跷跷板的中点)至地面的距离是50cm,当小红从水平位置 CD下降 30cm时,这时小明离地面的高度是________cm.
11.教室里有几盆花,如图1,测量这几盆花两旁的A,B 两点间的距离不方便,因此,选点A,B 都能到达的一点O,如图 2,连接BO并延长BO 到点C,使 CO=BO,连接AO并延长AO 到点 D,使 DO=AO.那么C,D两点间的距离就是A,B 两点间的距离.请说明理由.
12.如图,要测量河两岸上A,B 两点的距离,在点 B所在河岸一侧平地上取一点 C,使A,B,C在一条直线上,另取点 D,使 CD=BC,测得∠DCB=100°,∠ADC=65°,在CD的延长线上取点E,使 这时测得 DE的长就是A,B 两点的距离,为什么
13.如图所示,O为码头,A,B 两个灯塔与码头的距离相等,OA,OB为海岸线,一轮船从码头开出,计划沿 的平分线航行,航行途中,测得轮船与灯塔A,B的距离相
等,此时轮船有没有偏离航线 画出图形并说明你的理由.
参考答案
1. C 2. C 3. D 4. C 5. A
6.D 解析:由题意可知 OB=OC,
因为 所以90°,
所以,
在△COE 和△OBD中, 所以△COE≌△OBD(AAS),
所以CE=OD,OE=BD.
因为 BD,CE分别为 1.4m 和1.8m,所以DE=OD-OE=CE-BD=1.8-1.4=0.4(m),
因为 AD=1m,所以AE=AD+DE=1.4(m),
所以爸爸是在距离地面1.4m 的地方接住小丽的.
7.45 8.90° 9.3s 10.80
11.解:在△COD和△BOA 中,CO=BO,∠COD=∠BOA,DO=AO,所以△COD≌△BOA(SAS).
所以CD=AB.所以只要测出C,D两点间的距离就可知A,B两点间的距离.
12.证明:因为∠DCB=100°,∠ADC=65°,所以∠A=15°,所以∠BEC=∠A.
在△BCE和△DCA中, 所以△BCE≌△DCA(AAS),
所以AC=CE,
因为 所以 即
所以测得 DE的长就是A,B两点的距离.
13.解:此时轮船没有偏离航线.理由:
如图,由题意知( PB,所以
所以 所以此时轮船没有偏离航线.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
