第一章 三角形 章末复习(含答案)
图片预览


文档简介
中小学教育资源及组卷应用平台
第一章 三角形
章末复习
类型一 三角形的基本知识
1.如图所示,AB∥CD, EF⊥BD,垂足为点E,∠1=40°,则∠2 的度数为 ( )
A.50° B.40° C.45° D.25°
2.如图, 为 的中线,AP 为 的中线, 为△AP C 的中线,…,按此规律, 为 的中线.若△ABC 的面积为16,则的面积为( )
3.在△ABC中,有两边长分别是6 和7,已知第三边x的长度是5 的整数倍,则x的值可能是___________.
4.如图所示,平面上直线a,b分别经过线段OK 两端点,则a,b相交所成锐角的度数是___________.
第4题图 第5题图
5.如图,ED 是△EBC的一条中线, BE=CE,△ABC的周长为 40,则的周长为_____________.
6.已知是三角形的三边长,试化简
类型二 全等三角形的判定
7.如图,已知AB=AD,AC=AE,要证△ABC≌△ADE,可以添加的条件是 ( )
A.∠1=∠2 B.∠B=∠D C.∠C=∠E D.∠CAD=∠DAC
8.在△ABC 中,∠B=∠C=50°,将△ABC 沿图中虚线剪开,剪下的两个三角形不一定全等的是( )
9.已知:如图,在△ABC 和△DEF 中,点 B,E,C,F在同一条直线上,下面四个条件:①AB=DE ②AC=DF ③BE=CF ④∠ABC=∠DEF.
(1)请选择其中的三个条件,使得△ABC≌△DEF(写出一种情况即可);
(2) 在(1)的条件下,求证:△ABC≌△DEF.
类型三 全等三角形的实际应用
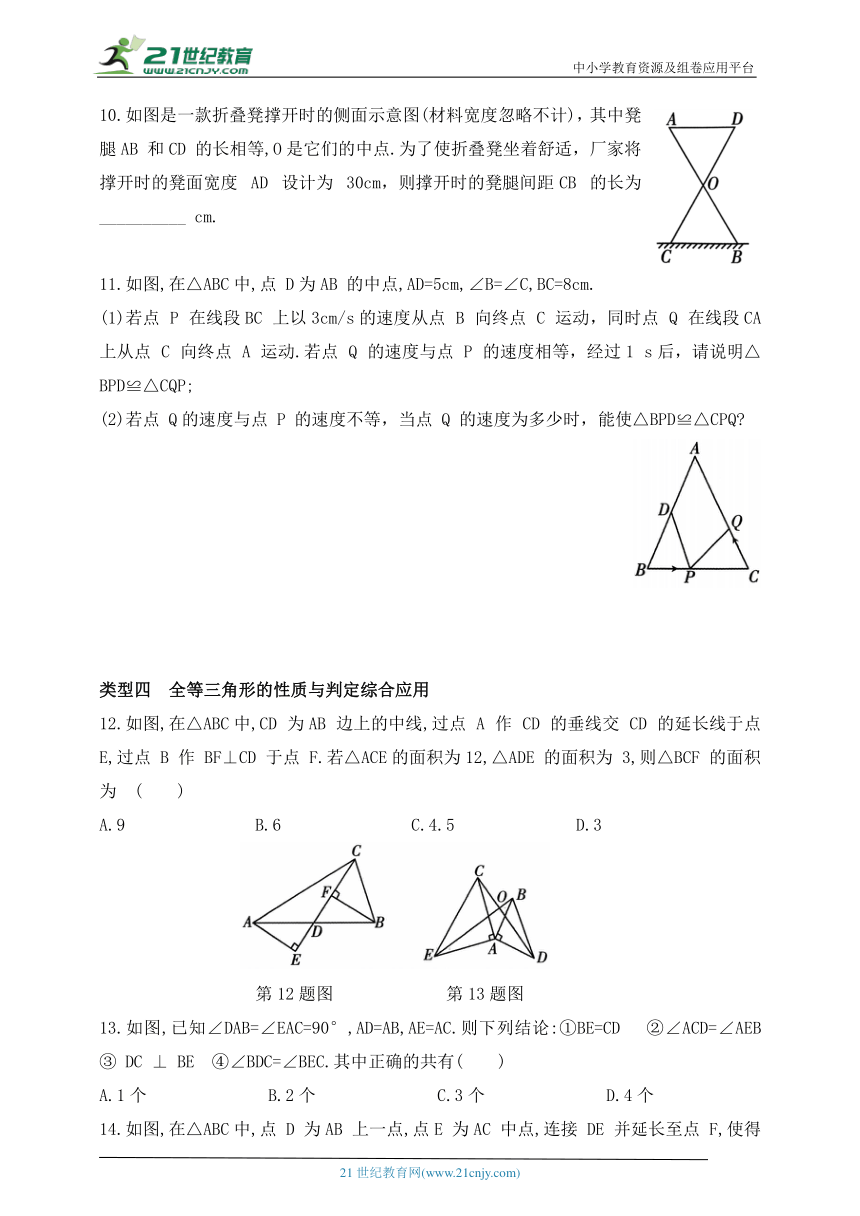
10.如图是一款折叠凳撑开时的侧面示意图(材料宽度忽略不计),其中凳腿AB 和CD 的长相等,O是它们的中点.为了使折叠凳坐着舒适,厂家将撑开时的凳面宽度 AD 设计为 30cm,则撑开时的凳腿间距CB 的长为__________ cm.
11.如图,在△ABC中,点 D为AB 的中点,AD=5cm,∠B=∠C,BC=8cm.
(1)若点 P 在线段BC 上以3cm/s的速度从点 B 向终点 C 运动,同时点 Q 在线段CA 上从点 C 向终点 A 运动.若点 Q 的速度与点 P 的速度相等,经过1 s后,请说明△BPD≌△CQP;
(2)若点 Q的速度与点 P 的速度不等,当点 Q 的速度为多少时,能使△BPD≌△CPQ
类型四 全等三角形的性质与判定综合应用
12.如图,在△ABC中,CD 为AB 边上的中线,过点 A 作 CD 的垂线交 CD 的延长线于点 E,过点 B 作 BF⊥CD 于点 F.若△ACE的面积为12,△ADE 的面积为 3,则△BCF 的面积为 ( )
A.9 B.6 C.4.5 D.3
第12题图 第13题图
13.如图,已知∠DAB=∠EAC=90°,AD=AB,AE=AC.则下列结论:①BE=CD ②∠ACD=∠AEB ③ DC ⊥ BE ④∠BDC=∠BEC.其中正确的共有( )
A.1个 B.2个 C.3个 D.4个
14.如图,在△ABC中,点 D 为AB 上一点,点E 为AC 中点,连接 DE 并延长至点 F,使得EF=ED,连接CF.
(1)求证:CF∥AB;
(2)若∠ABC= 50°,连接 BE,BE 平分∠ABC,AC平分∠BCF,求∠A 的度数.
易错点 忽视全等判定中边角的顺序造成答案错误
15.如图,点 E,点F在BC上,BE=CF,∠B=∠C,添加一个条件,不能证明△ABF≌△DCE的是 ( )
A.∠A=∠D B.∠AFB=∠DEC C. AB=DC D. AF=DE
参考答案
1. A 2. D 3.5 或 10 4.30° 5.24
6.解:根据三角形的三边关系,两边之和大于第三边,
得,
所以
7. A
8. D 解析:A.根据SAS可以推出剪下的两个三角形全等,故 A 选项不符合题意;B.根据SAS可以推出剪下的两个三角形全等,故 B选项不符合题意;
C.如图 1:
因为∠B+∠BDF=180°-∠DFB,∠DFC=180°-∠DFB,所以∠DFC=∠B+∠BDF,
又因为∠DFC=∠DFE+∠EFC,所以∠DFE+∠EFC=∠B+∠BDF,
因为∠B=∠DFE=50°,所以∠EFC=∠BDF,
因为 BD=FC,∠B=∠C,所以△DBF≌△FCE(ASA).
根据ASA 可以推出剪下的两个三角形全等,
故 C 选项不符合题意;
D.如图2:
由C选项可得∠EFC=∠BDF,∠B=∠C,但EC不是两个角的夹边,所以两个三角形不一定全等,故 D选项符合题意.
9.解:(1)由题知,选择的三个条件是:①②③;或者选择的三个条件是:①③④.
(2)证明:当选择①②③时,
因为 BE=CF,所以BE+EC=CF+EC,即 BC=EF,
在△ABC和△DEF中, 所以△ABC≌△DEF(SSS);
当选择①③④时,
因为 BE=CF,所以BE+EC=CF+EC,即 BC=EF.
在△ABC和△DEF中, 所以△ABC≌△DEF(SAS).
10.30
11.解:(1)因为 BP=3×1=3(cm),CQ=3×1=3(cm),所以 BP=CQ.因为点 D 为AB 的中点,
所以BD=AD=5cm.
因为CP=BC-BP=8-3=5(cm),所以 BD=CP.
又因为∠B=∠C,所以△BPD≌△CQP(SAS);
(2)设点 Q 的运动时间为 t s,运动速度为v cm/s.
因为△BPD≌△CPQ,所以 BP=CP=4 cm,BD=CQ=5cm,
所以 所以
所以当点 Q的运动速度为 时,能使△BPD≌△CPQ.
12. B 13. C
14.解:(1)证明:因为点 E 为 AC 中点,所以AE=CE,
在△AED和△CEF中, 所以△AED≌△CEF(SAS),
所以∠A=∠ACF,所以CF∥AB;
(2)因为 AC 平分∠BCF,所以∠ACB=∠ACF,
因为∠A=∠ACF,所以∠A=∠ACB,
因为∠A+∠ABC+∠ACB=180°,∠ABC=50°,
所以2∠A=130°,所以∠A=65°.
15. D
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第一章 三角形
章末复习
类型一 三角形的基本知识
1.如图所示,AB∥CD, EF⊥BD,垂足为点E,∠1=40°,则∠2 的度数为 ( )
A.50° B.40° C.45° D.25°
2.如图, 为 的中线,AP 为 的中线, 为△AP C 的中线,…,按此规律, 为 的中线.若△ABC 的面积为16,则的面积为( )
3.在△ABC中,有两边长分别是6 和7,已知第三边x的长度是5 的整数倍,则x的值可能是___________.
4.如图所示,平面上直线a,b分别经过线段OK 两端点,则a,b相交所成锐角的度数是___________.
第4题图 第5题图
5.如图,ED 是△EBC的一条中线, BE=CE,△ABC的周长为 40,则的周长为_____________.
6.已知是三角形的三边长,试化简
类型二 全等三角形的判定
7.如图,已知AB=AD,AC=AE,要证△ABC≌△ADE,可以添加的条件是 ( )
A.∠1=∠2 B.∠B=∠D C.∠C=∠E D.∠CAD=∠DAC
8.在△ABC 中,∠B=∠C=50°,将△ABC 沿图中虚线剪开,剪下的两个三角形不一定全等的是( )
9.已知:如图,在△ABC 和△DEF 中,点 B,E,C,F在同一条直线上,下面四个条件:①AB=DE ②AC=DF ③BE=CF ④∠ABC=∠DEF.
(1)请选择其中的三个条件,使得△ABC≌△DEF(写出一种情况即可);
(2) 在(1)的条件下,求证:△ABC≌△DEF.
类型三 全等三角形的实际应用
10.如图是一款折叠凳撑开时的侧面示意图(材料宽度忽略不计),其中凳腿AB 和CD 的长相等,O是它们的中点.为了使折叠凳坐着舒适,厂家将撑开时的凳面宽度 AD 设计为 30cm,则撑开时的凳腿间距CB 的长为__________ cm.
11.如图,在△ABC中,点 D为AB 的中点,AD=5cm,∠B=∠C,BC=8cm.
(1)若点 P 在线段BC 上以3cm/s的速度从点 B 向终点 C 运动,同时点 Q 在线段CA 上从点 C 向终点 A 运动.若点 Q 的速度与点 P 的速度相等,经过1 s后,请说明△BPD≌△CQP;
(2)若点 Q的速度与点 P 的速度不等,当点 Q 的速度为多少时,能使△BPD≌△CPQ
类型四 全等三角形的性质与判定综合应用
12.如图,在△ABC中,CD 为AB 边上的中线,过点 A 作 CD 的垂线交 CD 的延长线于点 E,过点 B 作 BF⊥CD 于点 F.若△ACE的面积为12,△ADE 的面积为 3,则△BCF 的面积为 ( )
A.9 B.6 C.4.5 D.3
第12题图 第13题图
13.如图,已知∠DAB=∠EAC=90°,AD=AB,AE=AC.则下列结论:①BE=CD ②∠ACD=∠AEB ③ DC ⊥ BE ④∠BDC=∠BEC.其中正确的共有( )
A.1个 B.2个 C.3个 D.4个
14.如图,在△ABC中,点 D 为AB 上一点,点E 为AC 中点,连接 DE 并延长至点 F,使得EF=ED,连接CF.
(1)求证:CF∥AB;
(2)若∠ABC= 50°,连接 BE,BE 平分∠ABC,AC平分∠BCF,求∠A 的度数.
易错点 忽视全等判定中边角的顺序造成答案错误
15.如图,点 E,点F在BC上,BE=CF,∠B=∠C,添加一个条件,不能证明△ABF≌△DCE的是 ( )
A.∠A=∠D B.∠AFB=∠DEC C. AB=DC D. AF=DE
参考答案
1. A 2. D 3.5 或 10 4.30° 5.24
6.解:根据三角形的三边关系,两边之和大于第三边,
得,
所以
7. A
8. D 解析:A.根据SAS可以推出剪下的两个三角形全等,故 A 选项不符合题意;B.根据SAS可以推出剪下的两个三角形全等,故 B选项不符合题意;
C.如图 1:
因为∠B+∠BDF=180°-∠DFB,∠DFC=180°-∠DFB,所以∠DFC=∠B+∠BDF,
又因为∠DFC=∠DFE+∠EFC,所以∠DFE+∠EFC=∠B+∠BDF,
因为∠B=∠DFE=50°,所以∠EFC=∠BDF,
因为 BD=FC,∠B=∠C,所以△DBF≌△FCE(ASA).
根据ASA 可以推出剪下的两个三角形全等,
故 C 选项不符合题意;
D.如图2:
由C选项可得∠EFC=∠BDF,∠B=∠C,但EC不是两个角的夹边,所以两个三角形不一定全等,故 D选项符合题意.
9.解:(1)由题知,选择的三个条件是:①②③;或者选择的三个条件是:①③④.
(2)证明:当选择①②③时,
因为 BE=CF,所以BE+EC=CF+EC,即 BC=EF,
在△ABC和△DEF中, 所以△ABC≌△DEF(SSS);
当选择①③④时,
因为 BE=CF,所以BE+EC=CF+EC,即 BC=EF.
在△ABC和△DEF中, 所以△ABC≌△DEF(SAS).
10.30
11.解:(1)因为 BP=3×1=3(cm),CQ=3×1=3(cm),所以 BP=CQ.因为点 D 为AB 的中点,
所以BD=AD=5cm.
因为CP=BC-BP=8-3=5(cm),所以 BD=CP.
又因为∠B=∠C,所以△BPD≌△CQP(SAS);
(2)设点 Q 的运动时间为 t s,运动速度为v cm/s.
因为△BPD≌△CPQ,所以 BP=CP=4 cm,BD=CQ=5cm,
所以 所以
所以当点 Q的运动速度为 时,能使△BPD≌△CPQ.
12. B 13. C
14.解:(1)证明:因为点 E 为 AC 中点,所以AE=CE,
在△AED和△CEF中, 所以△AED≌△CEF(SAS),
所以∠A=∠ACF,所以CF∥AB;
(2)因为 AC 平分∠BCF,所以∠ACB=∠ACF,
因为∠A=∠ACF,所以∠A=∠ACB,
因为∠A+∠ABC+∠ACB=180°,∠ABC=50°,
所以2∠A=130°,所以∠A=65°.
15. D
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
