平面向量复习
图片预览


文档简介
平 面 向 量 复 习
教学目标:理解向量的相关概念、向量的运算、向量的应用
教学重难点:几个重要概念的理解、数量积与数乘运算的区别、求向量的夹角
重要知识点提要:
一、向量的相关概念:
1)定义:既有大小又有方向的量叫向量。
2)重要概念:
(1)零向量:长度为0的向量,记作0.
(2)单位向量:长度为1个单位长度的向量.
(3)平行向量:也叫共线向量,方向相同或相反
的非零向量.
(4)相等向量:长度相等且方向相同的向量.
(5)相反向量:长度相等且方向相反的向量.
向量的表示:
几何表示:有向线段
字母表示
坐标表示: (x,y)
二、向量的运算
1)加法:
①两个法则
三角形法则
重要结论:AB+BC+CA= 0
平行四边形法则
②坐标表示:设 a = (x1, y1), b = (x2, y2)
则a + b =( x1 + x2 , y1 + y2 )
2)减法:
①减法法则:
OA-OB =BA
②坐标运算:
若 a=( x1, y1 ), b=( x2, y2 )
则a - b= (x1 - x2 , y1 - y2)
3)运算律
加法减法运算率
(1)交换律:a+b=b+a
(2)结合律:(a+b)+c=a+(b+c)
(3)实数λ与向量 a 的积
定义:λa是一个向量. 它的长度 |λa| =|λ| |a|;
它的方向
(1) 当λ≥0时,λa 的方向与a方向相同;
(2) 当λ<0时,λa 的方向与a方向相反.
其实质就是向量的伸长或缩短!
4)坐标运算:
若a = (x , y), 则λa = λ (x , y) = (λ x , λ y)
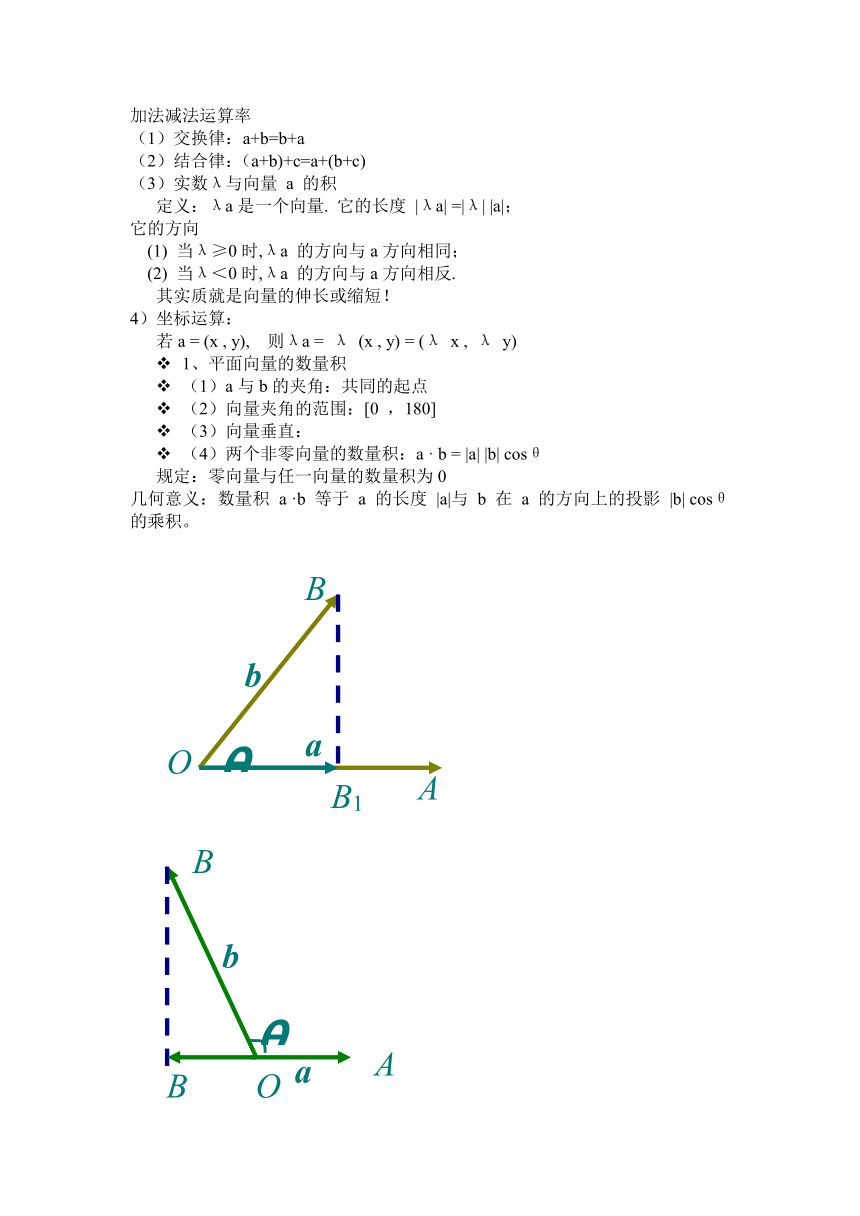
1、平面向量的数量积
(1)a与b的夹角:共同的起点
(2)向量夹角的范围:[0 ,180]
(3)向量垂直:
(4)两个非零向量的数量积:a · b = |a| |b| cosθ
规定:零向量与任一向量的数量积为0
几何意义:数量积 a ·b 等于 a 的长度 |a|与 b 在 a 的方向上的投影 |b| cosθ的乘积。
5)数量积的运算律:
⑴交换律:
⑵对数乘的结合律:
⑶分配律:
注意:数量积不满足结合律
ab为非零向量,e为单位向量
(1)e· a = a · e =| a | cosθ
(2)a ⊥ b的充要条件是 a · b =0
(3) 当 a与b同向时, a · b = |a | | b | ;
当 a 与b 反向时,a · b = - |a | | b |
特别地:a · a=| a | 2 或 | a | =
(4)cosθ= (5)| a·b | ≤ | a | | b |
6)向量的模(长度)
1. 设 a = ( x , y ), 则
2. 若表示向量 a 的起点和终点的坐标分别
为A(x1,y1)、B (x2,y2) ,则
3.向量的加法运算
三、平面向量之间关系
1、向量平行(共线)充要条件的两种形式:
2、向量垂直充要条件的两种形式:
(3)两个向量相等的充要条件是两个向量的坐标相等.
即:
那么
四、平面向量的基本定理
如果 是同一平面内的两个不共线向量,那么对于这一平面内的任一向量 ,有且只有一对实数
使
典例讲解:
例1、设AB=2(a+5b),BC= 2a + 8b,CD=3(a b),求证:A、B、D 三点共线。
例2、若向量 =(-3,4),则 按向量 =(2,-1)平移后的坐标为_____.
例3、给出下列命题:①若|a|=|b|,则a=b;②若A,B,C,D是不共线的四点,则AB= DC是四边形ABCD为平行四边形的充要条件;③若a=b,b=c,则a=c;④a=b的充要条件是|a|=|b|且a∥b;⑤若a∥b,b∥c,则a∥c
其中,正确命题的序号是______
例4、已知a,b方向相同,且|a|=3,|b|=7,则|2a-b|=___________
例5、若将向量a=(2,1)绕原点按逆时针方向旋转 得到向量b,则向量b的坐标为_____
例6、下列算式中不正确的是( )
(A) AB+BC+CA=0 (B) AB-AC=BC
(C) 0·AB=0 (D)λ(μa)=(λμ)a
例7、设P、Q是四边形ABCD对角线AC、BD中点,BC=a,DA=b,则 PQ=_________
例8、若a、b、c是非零的平面向量,其中任意两个向量都不共线,则( ) (A)(a)2·(b)2=(a·b)2 (B)|a+b|>|a-b| (C)(a·b)·c-(b·c)·a与b垂直 (D)(a·b)·c-(b·c)·a=0
例9、设a=(1,0),b=(1,1),且(a+λb)⊥b,则实数λ的值是( )
(A)2 (B)0 (C)1 (D)-1/2
例10、在三角形ABC中, =(2,3), =(1,k),且三角形ABC的一个内角为直角,求实数k的值
回家作业:
1、 判断下列命题正确与否?
1 若,则;
1 若向量,则按平移后的坐标仍是;
1 若,则=;
1 若,则,中至少有一个为;
1
1 的顶点A、B、C分别对应向量,,,则重心对应向量为;
1 //存在不全为零的实数,使;
2、已知=,,求值,使且
3、 已知点O是形内的一点,设,且,试用和表示;
3、 设向量
a) 当为何值时,A、B、C三点共线?
a) 当为何值时,
3、 设始点为同一点O的向量的终点A、B、C在同一条直线上,根据下列条件,把用表示出来:①c为线段AB的中点②c为以3:2内分线段AB的分点③C为以3:1外分线段AB的分点;
A
a
b
θ
B
B1
O
B
A
θ
b
B1
a
O
B
b
(B1)
A
a
O
A
y
B
C
O
x
教学目标:理解向量的相关概念、向量的运算、向量的应用
教学重难点:几个重要概念的理解、数量积与数乘运算的区别、求向量的夹角
重要知识点提要:
一、向量的相关概念:
1)定义:既有大小又有方向的量叫向量。
2)重要概念:
(1)零向量:长度为0的向量,记作0.
(2)单位向量:长度为1个单位长度的向量.
(3)平行向量:也叫共线向量,方向相同或相反
的非零向量.
(4)相等向量:长度相等且方向相同的向量.
(5)相反向量:长度相等且方向相反的向量.
向量的表示:
几何表示:有向线段
字母表示
坐标表示: (x,y)
二、向量的运算
1)加法:
①两个法则
三角形法则
重要结论:AB+BC+CA= 0
平行四边形法则
②坐标表示:设 a = (x1, y1), b = (x2, y2)
则a + b =( x1 + x2 , y1 + y2 )
2)减法:
①减法法则:
OA-OB =BA
②坐标运算:
若 a=( x1, y1 ), b=( x2, y2 )
则a - b= (x1 - x2 , y1 - y2)
3)运算律
加法减法运算率
(1)交换律:a+b=b+a
(2)结合律:(a+b)+c=a+(b+c)
(3)实数λ与向量 a 的积
定义:λa是一个向量. 它的长度 |λa| =|λ| |a|;
它的方向
(1) 当λ≥0时,λa 的方向与a方向相同;
(2) 当λ<0时,λa 的方向与a方向相反.
其实质就是向量的伸长或缩短!
4)坐标运算:
若a = (x , y), 则λa = λ (x , y) = (λ x , λ y)
1、平面向量的数量积
(1)a与b的夹角:共同的起点
(2)向量夹角的范围:[0 ,180]
(3)向量垂直:
(4)两个非零向量的数量积:a · b = |a| |b| cosθ
规定:零向量与任一向量的数量积为0
几何意义:数量积 a ·b 等于 a 的长度 |a|与 b 在 a 的方向上的投影 |b| cosθ的乘积。
5)数量积的运算律:
⑴交换律:
⑵对数乘的结合律:
⑶分配律:
注意:数量积不满足结合律
ab为非零向量,e为单位向量
(1)e· a = a · e =| a | cosθ
(2)a ⊥ b的充要条件是 a · b =0
(3) 当 a与b同向时, a · b = |a | | b | ;
当 a 与b 反向时,a · b = - |a | | b |
特别地:a · a=| a | 2 或 | a | =
(4)cosθ= (5)| a·b | ≤ | a | | b |
6)向量的模(长度)
1. 设 a = ( x , y ), 则
2. 若表示向量 a 的起点和终点的坐标分别
为A(x1,y1)、B (x2,y2) ,则
3.向量的加法运算
三、平面向量之间关系
1、向量平行(共线)充要条件的两种形式:
2、向量垂直充要条件的两种形式:
(3)两个向量相等的充要条件是两个向量的坐标相等.
即:
那么
四、平面向量的基本定理
如果 是同一平面内的两个不共线向量,那么对于这一平面内的任一向量 ,有且只有一对实数
使
典例讲解:
例1、设AB=2(a+5b),BC= 2a + 8b,CD=3(a b),求证:A、B、D 三点共线。
例2、若向量 =(-3,4),则 按向量 =(2,-1)平移后的坐标为_____.
例3、给出下列命题:①若|a|=|b|,则a=b;②若A,B,C,D是不共线的四点,则AB= DC是四边形ABCD为平行四边形的充要条件;③若a=b,b=c,则a=c;④a=b的充要条件是|a|=|b|且a∥b;⑤若a∥b,b∥c,则a∥c
其中,正确命题的序号是______
例4、已知a,b方向相同,且|a|=3,|b|=7,则|2a-b|=___________
例5、若将向量a=(2,1)绕原点按逆时针方向旋转 得到向量b,则向量b的坐标为_____
例6、下列算式中不正确的是( )
(A) AB+BC+CA=0 (B) AB-AC=BC
(C) 0·AB=0 (D)λ(μa)=(λμ)a
例7、设P、Q是四边形ABCD对角线AC、BD中点,BC=a,DA=b,则 PQ=_________
例8、若a、b、c是非零的平面向量,其中任意两个向量都不共线,则( ) (A)(a)2·(b)2=(a·b)2 (B)|a+b|>|a-b| (C)(a·b)·c-(b·c)·a与b垂直 (D)(a·b)·c-(b·c)·a=0
例9、设a=(1,0),b=(1,1),且(a+λb)⊥b,则实数λ的值是( )
(A)2 (B)0 (C)1 (D)-1/2
例10、在三角形ABC中, =(2,3), =(1,k),且三角形ABC的一个内角为直角,求实数k的值
回家作业:
1、 判断下列命题正确与否?
1 若,则;
1 若向量,则按平移后的坐标仍是;
1 若,则=;
1 若,则,中至少有一个为;
1
1 的顶点A、B、C分别对应向量,,,则重心对应向量为;
1 //存在不全为零的实数,使;
2、已知=,,求值,使且
3、 已知点O是形内的一点,设,且,试用和表示;
3、 设向量
a) 当为何值时,A、B、C三点共线?
a) 当为何值时,
3、 设始点为同一点O的向量的终点A、B、C在同一条直线上,根据下列条件,把用表示出来:①c为线段AB的中点②c为以3:2内分线段AB的分点③C为以3:1外分线段AB的分点;
A
a
b
θ
B
B1
O
B
A
θ
b
B1
a
O
B
b
(B1)
A
a
O
A
y
B
C
O
x
