【人教版数学九年级上册同步练习】 23.1图形的旋转(含答案)
文档属性
| 名称 | 【人教版数学九年级上册同步练习】 23.1图形的旋转(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 4.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-25 13:45:50 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
【人教版数学九年级上册同步练习】
23.1图形的旋转
一、单选题
1.下列说法正确的有( )个
①三角形的一个外角大于它的任何一个内角
②若一个三角形的三个内角度数的比为,则这个三角形是直角三角形
③长方形既是中心对称图形又是轴对称图形
④如图,图形绕着中心旋转或或后能与自身重合
A.1 B.2 C.3 D.4
2.一个数学游戏,正六边形被平均分为6格(其中1格涂有阴影),规则如下:若第一个正六边形下面标的数字为a(a为正整数),则先绕正六边形的中心顺时针旋转a格;再沿某条边所在的直线l翻折,得到第二个图形。例如:若第一个正六边形下面标的数字为2,如图,则先绕其中心顺时针旋转2格;再沿直线l翻折,得到第二个图形。若第一个正六边形下面标的数字为4,如图,按照游戏规则,得到第二个图形应是( )
A. B.
C. D.
3.如图,将 绕顶点C旋转得到 ,且点B刚好落在 上,若 , ,则 等于( )
A. B. C. D.
4.下列图形绕某点旋转后,不能与原来图形重合的是(旋转度数不超过180°)( )
A. B. C. D.
5.如图,是由绕点顺时针旋转得到的.若点恰好在的延长线上,且,则等于( )
A.120° B.125° C.130° D.135°
二、填空题
6.一个正五角星绕着它的中心至少旋转 度能与自身重合.
7.如图,将以点为旋转中心逆时针旋转得到,当点在边上时,恰好有,若,则旋转角 , .
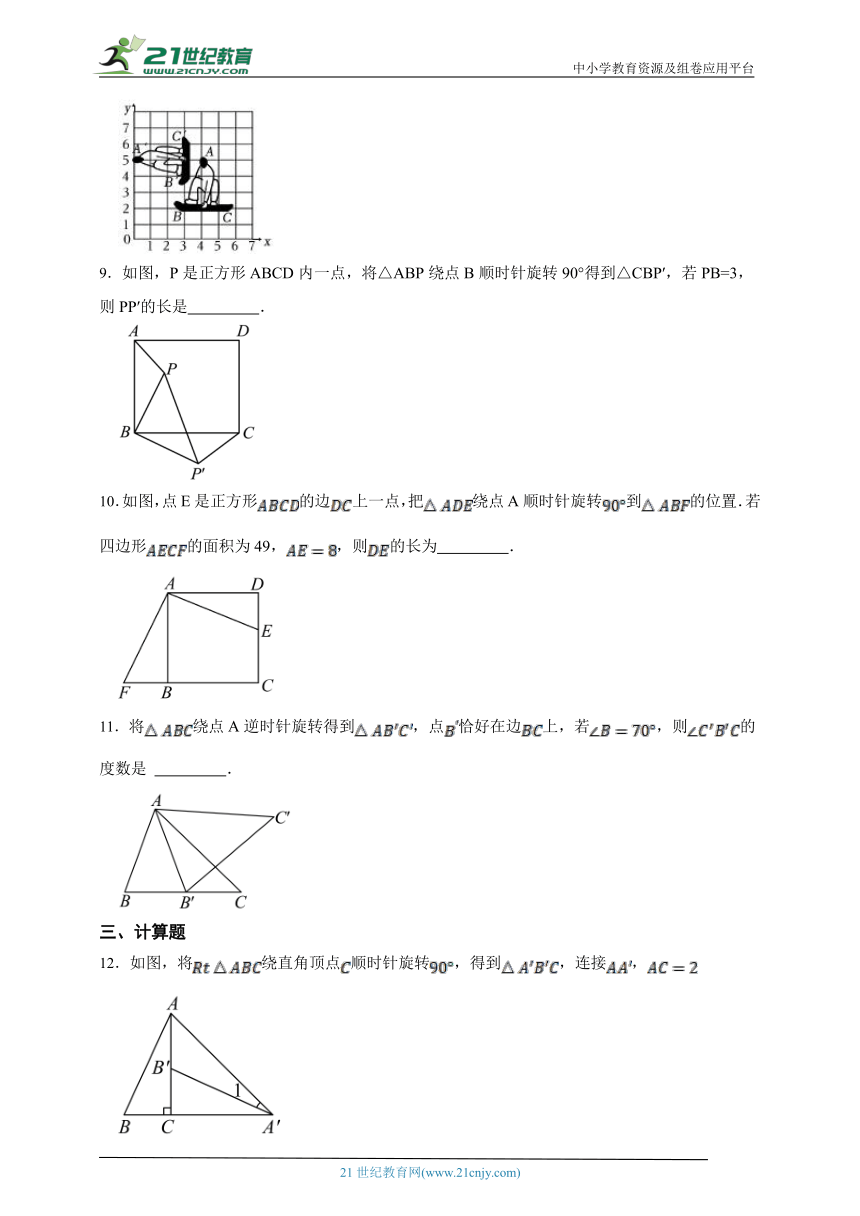
8.在冬奥会单板滑雪项目中,运动员的空中姿态优美飘逸.如图,在平面直角坐标系中,将我国运动员的初始位置用△ABC标记,则他在空中的运动可看成从初始位置绕某旋转中心逆时针旋转一定角度后到达另一位置,记为△A′B′C′,在这一过程中,旋转中心的坐标是 .
9.如图,P是正方形ABCD内一点,将△ABP绕点B顺时针旋转90°得到△CBP′,若PB=3,则PP′的长是 .
10.如图,点E是正方形的边上一点,把绕点A顺时针旋转到的位置.若四边形的面积为49,,则的长为 .
11.将绕点A逆时针旋转得到,点恰好在边上,若,则的度数是 .
三、计算题
12.如图,将绕直角顶点顺时针旋转,得到,连接,
(1)求的长
(2)若,求的度数.
四、解答题
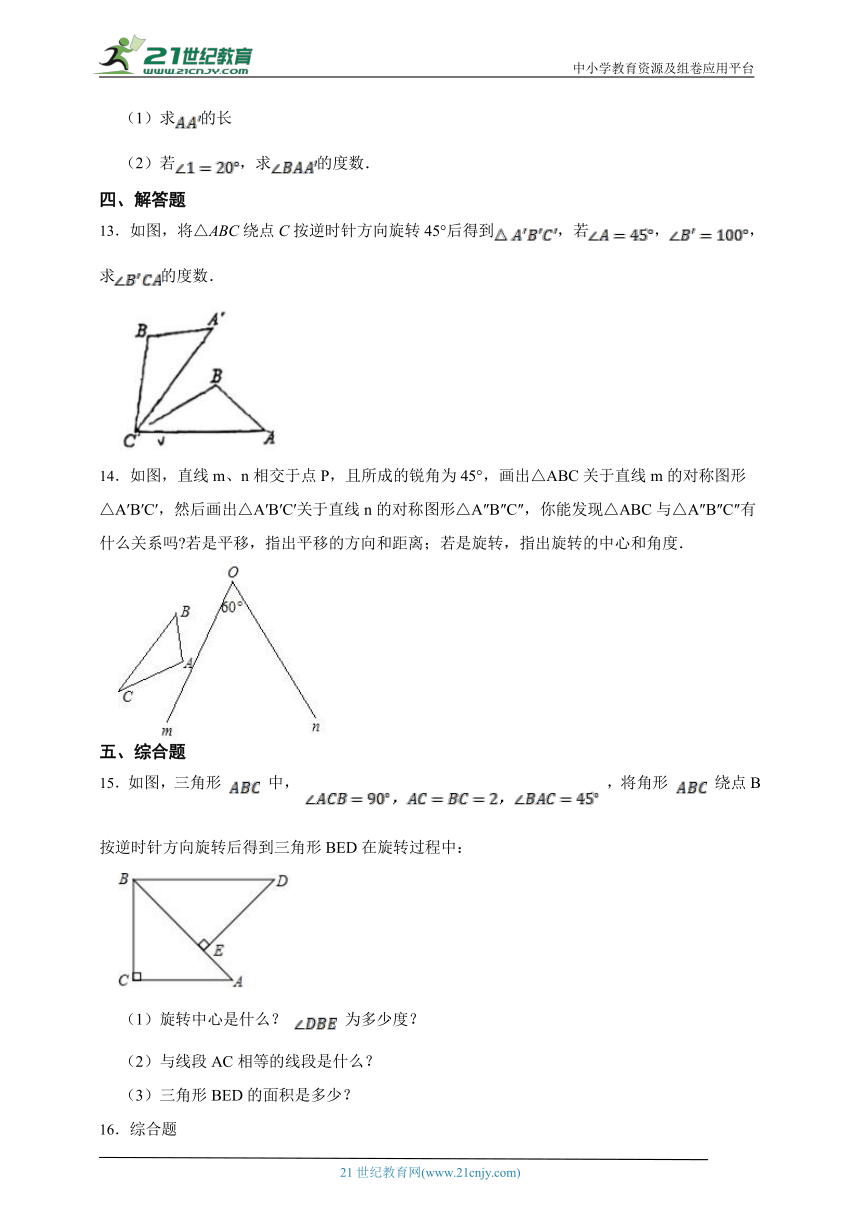
13.如图,将△ABC绕点C按逆时针方向旋转45°后得到,若,,求的度数.
14.如图,直线m、n相交于点P,且所成的锐角为45°,画出△ABC关于直线m的对称图形△A′B′C′,然后画出△A′B′C′关于直线n的对称图形△A″B″C″,你能发现△ABC与△A″B″C″有什么关系吗 若是平移,指出平移的方向和距离;若是旋转,指出旋转的中心和角度.
五、综合题
15.如图,三角形 中, ,将角形 绕点B按逆时针方向旋转后得到三角形BED在旋转过程中:
(1)旋转中心是什么? 为多少度?
(2)与线段AC相等的线段是什么?
(3)三角形BED的面积是多少?
16.综合题
(1)如图①所示,P是等边△ABC内的一点,连接PA、PB、PC,将△BAP绕B点顺时针旋转60°得△BCQ,连接PQ.若PA2+PB2=PC2,证明∠PQC=90°;
(2)如图②所示,P是等腰直角△ABC(∠ABC=90°)内的一点,连接PA、PB、PC,将△BAP绕B点顺时针旋转90°得△BCQ,连接PQ.当PA、PB、PC满足什么条件时,∠PQC=90°?请说明.
17.如图,方格纸中每个小正方形的边长都是单位1,△ABC在平面直角坐标系中的位置如图所示.
(1)将△ABC绕点O顺时针方向旋转90°后得△A1B1C1,画出△A1B1C1并直接写出点C1的坐标为 ;
(2)以原点O为位似中心,在第四象限画一个△A2B2C2,使它与△ABC位似,并且△A2B2C2与△ABC的相似比为2:1.
六、实践探究题
18.数学综合实践课上,小明用一块直角三角板进行探究:将三角板的直角顶点O放在直线上,将边落在射线上,边位于直线上方,三角板 绕点O顺时针旋转,旋转角为a,作直线平分交所在直线于点E.
(1)提出问题:如图1,若旋转角,求的度数;
(2)探索发现:如图2,若旋转角时,求的值;
(3)拓展探究:继续旋转三角板,若旋转角时,此时与还存在(2)中的结论吗?若存在,说明理由;如不存在,直接写出与之间的关系.
答案解析部分
1.【答案】C
【知识点】三角形内角和定理;三角形的外角性质;旋转的性质;中心对称及中心对称图形
2.【答案】A
【知识点】翻折变换(折叠问题);图形的旋转
3.【答案】D
【知识点】三角形的外角性质;等腰三角形的性质;旋转的性质
4.【答案】D
【知识点】旋转对称图形
5.【答案】C
【知识点】多边形内角与外角;旋转的性质
6.【答案】72
【知识点】旋转的性质
7.【答案】;
【知识点】等腰三角形的性质;旋转的性质;内错角的概念
8.【答案】(2,3)
【知识点】图形的旋转;旋转对称图形
9.【答案】
【知识点】勾股定理;旋转的性质
10.【答案】
【知识点】勾股定理;正方形的性质;旋转的性质
11.【答案】
【知识点】等腰三角形的性质;旋转的性质
12.【答案】(1)
(2)
【知识点】三角形内角和定理;勾股定理;旋转的性质
13.【答案】解:∵旋转
∴,,
∵
∴
∴.
【知识点】旋转的性质
14.【答案】解:△A″B″C″可由△ABC 顺时针 旋转得到,旋转的中心是点P, 旋转的角度为90°.图略
【知识点】旋转对称图形
15.【答案】(1)解:∵∠ACB=90°,AC=BC=2.∠BAC=45°,
∴∠ABC=45°
∵将三角形ABC绕点B按逆时针方向旋转后得到三角形BED,
∴旋转中心为点B,∠DBE=∠ABC=45°
(2)解:∵将三角形ABC绕点B按逆时针方向旋转后得到三角形BED,
∴BE=BC,AC=DE
∵AC=BC
∴AC=DE=BE=BC
∴与线段AC相等的线段是DE,BE,BC;
(3)解:∵BE=BC=2,AC=DE=2
∴S△BDE= ×2×2=2.
【知识点】三角形的面积;旋转的性质
16.【答案】(1)证明:由旋转的性质知:BP=BQ、PA=QC,∠ABP=∠CBQ;
∵△ABC是等边三角形,
∴∠ABC=60°,即∠CBP+∠ABP=60°;
∵∠ABP=∠CBQ,
∴∠CBP+∠CBQ=60°,即∠PBQ=60°;
又∵BP=BQ,∴△BPQ是等边三角形;
∴BP=PQ;
∵PA2+PB2=PC2,即PQ2+QC2=PC2;
∴△PQC是直角三角形,且∠PQC=90°
(2)解:PA2+2PB2=PC2;理由如下:
同(1)可得:△PBQ是等腰直角三角形,则PQ= PB,即PQ2=2PB2;
由旋转的性质知:PA=QC;
在△PQC中,若∠PQC=90°,则PQ2+QC2=PC2,即PA2+2PB2=PC2;
故当PA2+2PB2=PC2时,∠PQC=90°
【知识点】等边三角形的性质;等边三角形的判定;勾股定理的逆定理;旋转的性质
17.【答案】(1)(2,3)
(2)如图,△A2B2C2为所作.
【知识点】作图﹣位似变换;作图﹣旋转
18.【答案】(1)
(2)
(3)不存在,
【知识点】角的运算;余角、补角及其性质;旋转的性质
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【人教版数学九年级上册同步练习】
23.1图形的旋转
一、单选题
1.下列说法正确的有( )个
①三角形的一个外角大于它的任何一个内角
②若一个三角形的三个内角度数的比为,则这个三角形是直角三角形
③长方形既是中心对称图形又是轴对称图形
④如图,图形绕着中心旋转或或后能与自身重合
A.1 B.2 C.3 D.4
2.一个数学游戏,正六边形被平均分为6格(其中1格涂有阴影),规则如下:若第一个正六边形下面标的数字为a(a为正整数),则先绕正六边形的中心顺时针旋转a格;再沿某条边所在的直线l翻折,得到第二个图形。例如:若第一个正六边形下面标的数字为2,如图,则先绕其中心顺时针旋转2格;再沿直线l翻折,得到第二个图形。若第一个正六边形下面标的数字为4,如图,按照游戏规则,得到第二个图形应是( )
A. B.
C. D.
3.如图,将 绕顶点C旋转得到 ,且点B刚好落在 上,若 , ,则 等于( )
A. B. C. D.
4.下列图形绕某点旋转后,不能与原来图形重合的是(旋转度数不超过180°)( )
A. B. C. D.
5.如图,是由绕点顺时针旋转得到的.若点恰好在的延长线上,且,则等于( )
A.120° B.125° C.130° D.135°
二、填空题
6.一个正五角星绕着它的中心至少旋转 度能与自身重合.
7.如图,将以点为旋转中心逆时针旋转得到,当点在边上时,恰好有,若,则旋转角 , .
8.在冬奥会单板滑雪项目中,运动员的空中姿态优美飘逸.如图,在平面直角坐标系中,将我国运动员的初始位置用△ABC标记,则他在空中的运动可看成从初始位置绕某旋转中心逆时针旋转一定角度后到达另一位置,记为△A′B′C′,在这一过程中,旋转中心的坐标是 .
9.如图,P是正方形ABCD内一点,将△ABP绕点B顺时针旋转90°得到△CBP′,若PB=3,则PP′的长是 .
10.如图,点E是正方形的边上一点,把绕点A顺时针旋转到的位置.若四边形的面积为49,,则的长为 .
11.将绕点A逆时针旋转得到,点恰好在边上,若,则的度数是 .
三、计算题
12.如图,将绕直角顶点顺时针旋转,得到,连接,
(1)求的长
(2)若,求的度数.
四、解答题
13.如图,将△ABC绕点C按逆时针方向旋转45°后得到,若,,求的度数.
14.如图,直线m、n相交于点P,且所成的锐角为45°,画出△ABC关于直线m的对称图形△A′B′C′,然后画出△A′B′C′关于直线n的对称图形△A″B″C″,你能发现△ABC与△A″B″C″有什么关系吗 若是平移,指出平移的方向和距离;若是旋转,指出旋转的中心和角度.
五、综合题
15.如图,三角形 中, ,将角形 绕点B按逆时针方向旋转后得到三角形BED在旋转过程中:
(1)旋转中心是什么? 为多少度?
(2)与线段AC相等的线段是什么?
(3)三角形BED的面积是多少?
16.综合题
(1)如图①所示,P是等边△ABC内的一点,连接PA、PB、PC,将△BAP绕B点顺时针旋转60°得△BCQ,连接PQ.若PA2+PB2=PC2,证明∠PQC=90°;
(2)如图②所示,P是等腰直角△ABC(∠ABC=90°)内的一点,连接PA、PB、PC,将△BAP绕B点顺时针旋转90°得△BCQ,连接PQ.当PA、PB、PC满足什么条件时,∠PQC=90°?请说明.
17.如图,方格纸中每个小正方形的边长都是单位1,△ABC在平面直角坐标系中的位置如图所示.
(1)将△ABC绕点O顺时针方向旋转90°后得△A1B1C1,画出△A1B1C1并直接写出点C1的坐标为 ;
(2)以原点O为位似中心,在第四象限画一个△A2B2C2,使它与△ABC位似,并且△A2B2C2与△ABC的相似比为2:1.
六、实践探究题
18.数学综合实践课上,小明用一块直角三角板进行探究:将三角板的直角顶点O放在直线上,将边落在射线上,边位于直线上方,三角板 绕点O顺时针旋转,旋转角为a,作直线平分交所在直线于点E.
(1)提出问题:如图1,若旋转角,求的度数;
(2)探索发现:如图2,若旋转角时,求的值;
(3)拓展探究:继续旋转三角板,若旋转角时,此时与还存在(2)中的结论吗?若存在,说明理由;如不存在,直接写出与之间的关系.
答案解析部分
1.【答案】C
【知识点】三角形内角和定理;三角形的外角性质;旋转的性质;中心对称及中心对称图形
2.【答案】A
【知识点】翻折变换(折叠问题);图形的旋转
3.【答案】D
【知识点】三角形的外角性质;等腰三角形的性质;旋转的性质
4.【答案】D
【知识点】旋转对称图形
5.【答案】C
【知识点】多边形内角与外角;旋转的性质
6.【答案】72
【知识点】旋转的性质
7.【答案】;
【知识点】等腰三角形的性质;旋转的性质;内错角的概念
8.【答案】(2,3)
【知识点】图形的旋转;旋转对称图形
9.【答案】
【知识点】勾股定理;旋转的性质
10.【答案】
【知识点】勾股定理;正方形的性质;旋转的性质
11.【答案】
【知识点】等腰三角形的性质;旋转的性质
12.【答案】(1)
(2)
【知识点】三角形内角和定理;勾股定理;旋转的性质
13.【答案】解:∵旋转
∴,,
∵
∴
∴.
【知识点】旋转的性质
14.【答案】解:△A″B″C″可由△ABC 顺时针 旋转得到,旋转的中心是点P, 旋转的角度为90°.图略
【知识点】旋转对称图形
15.【答案】(1)解:∵∠ACB=90°,AC=BC=2.∠BAC=45°,
∴∠ABC=45°
∵将三角形ABC绕点B按逆时针方向旋转后得到三角形BED,
∴旋转中心为点B,∠DBE=∠ABC=45°
(2)解:∵将三角形ABC绕点B按逆时针方向旋转后得到三角形BED,
∴BE=BC,AC=DE
∵AC=BC
∴AC=DE=BE=BC
∴与线段AC相等的线段是DE,BE,BC;
(3)解:∵BE=BC=2,AC=DE=2
∴S△BDE= ×2×2=2.
【知识点】三角形的面积;旋转的性质
16.【答案】(1)证明:由旋转的性质知:BP=BQ、PA=QC,∠ABP=∠CBQ;
∵△ABC是等边三角形,
∴∠ABC=60°,即∠CBP+∠ABP=60°;
∵∠ABP=∠CBQ,
∴∠CBP+∠CBQ=60°,即∠PBQ=60°;
又∵BP=BQ,∴△BPQ是等边三角形;
∴BP=PQ;
∵PA2+PB2=PC2,即PQ2+QC2=PC2;
∴△PQC是直角三角形,且∠PQC=90°
(2)解:PA2+2PB2=PC2;理由如下:
同(1)可得:△PBQ是等腰直角三角形,则PQ= PB,即PQ2=2PB2;
由旋转的性质知:PA=QC;
在△PQC中,若∠PQC=90°,则PQ2+QC2=PC2,即PA2+2PB2=PC2;
故当PA2+2PB2=PC2时,∠PQC=90°
【知识点】等边三角形的性质;等边三角形的判定;勾股定理的逆定理;旋转的性质
17.【答案】(1)(2,3)
(2)如图,△A2B2C2为所作.
【知识点】作图﹣位似变换;作图﹣旋转
18.【答案】(1)
(2)
(3)不存在,
【知识点】角的运算;余角、补角及其性质;旋转的性质
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
