第3讲 四边形2023-2024学年人教版三年级数学尖子生突破练习(含答案)
文档属性
| 名称 | 第3讲 四边形2023-2024学年人教版三年级数学尖子生突破练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 844.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-25 17:18:10 | ||
图片预览



文档简介
第3讲 四边形
专题概述
生活中,常常能看到有四条边、四个角的封闭图形,我们称之为四边形。在四边形当中还含有几种特殊的四边形——梯形、平行四边形、长方形和正方形。
梯形:只有一组对边平行的四边形。梯形中平行的一组对边分别叫“上底”和“下底”,不平行的一组对边皆叫“腰”。过梯形的一顶点,作该顶点所对应的边的垂线。我们称这条垂线为“高”,与之垂直的边为“底”。
梯形的面积=(上底+下底)×高÷2。
平行四边形:两组对边分别平行的四边形。平行四边形的对边平行且相等,对角也相等。相较于三角形的稳定性而言,平行四边形具有不稳定性。过平行四边形的一顶点,作该顶点所对应的边的垂线。我们称这条垂线为“高”,与之垂直的边为“底”。
平行四边形的面积=底×高。由公式可知,同底等高的平行四边形面积相等。
长方形:有一个角是直角的平行四边形。长方形是特殊的平行四边形,它不仅具有平行四边形所具有的所有性质,它的四个角还都为直角。我们一般称长方形中较长的那一条边为“长”,较短的那一条边为“宽”。
长方形的周长=(长+宽)×2;长方形的面积=长×宽。
正方形:一组邻边相等的长方形。正方形是特殊的长方形,在对边平行且相等,四个角都为直角的基础上,它的四条边都相等,我们一般称正方形的边为“边长”。
正方形的周长=边长×4;正方形的面积=边长×边长。
以上几种图形的关系可以用下图表示。
常用的面积单位有平方厘米( 平方分米 和平方米 相邻两个常用的面积单位之间的进率是100,即:
1平方分米=100平方厘米,
1平方米=100平方分米。
典型例题1
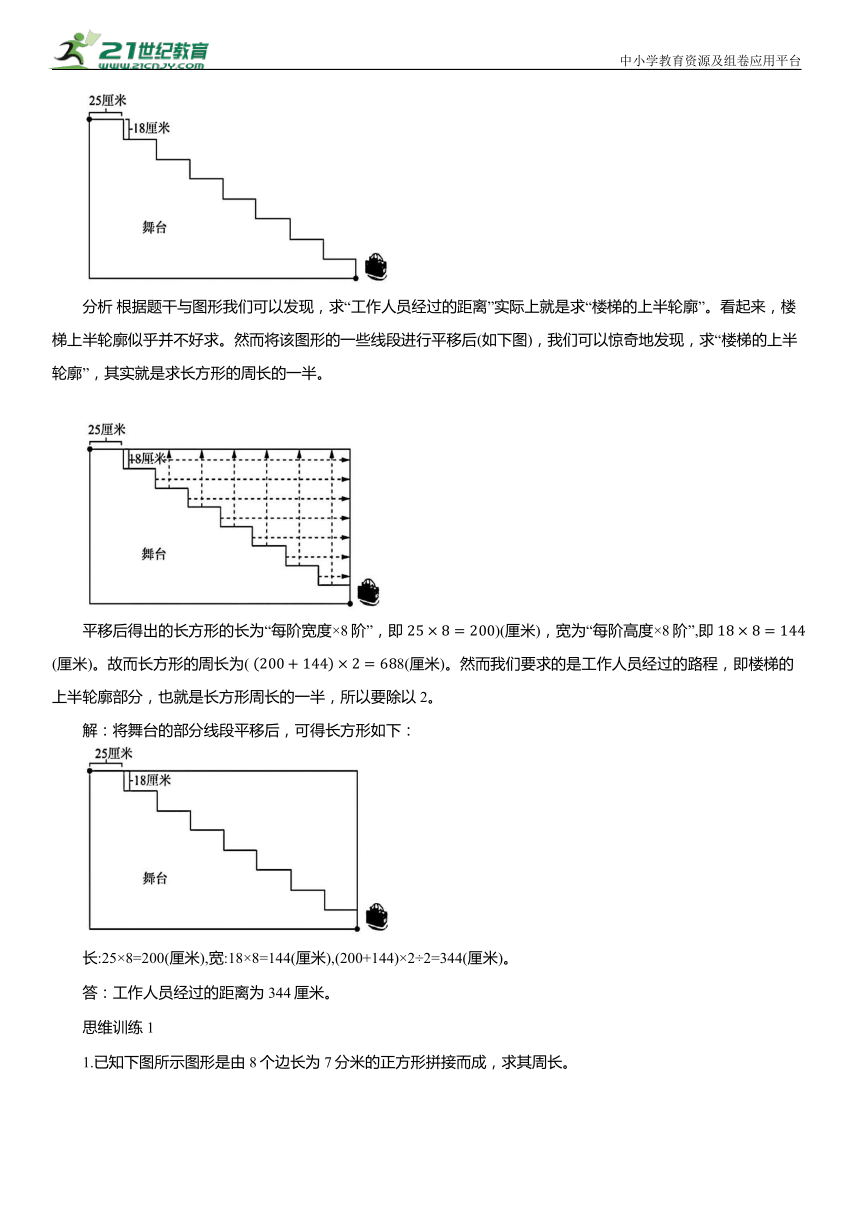
为庆祝“一带一路”国际合作高峰论坛在京顺利召开,某校决定举办一次文艺晚会。在搭设舞台之际,工作人员发现自己将工具包忘在舞台下,故而决定去拿。已知下舞台的楼梯共有8阶,每阶高度为18 厘米,宽度为25厘米(具体如下图所示),请问工作人员经过的距离有多长
分析 根据题干与图形我们可以发现,求“工作人员经过的距离”实际上就是求“楼梯的上半轮廓”。看起来,楼梯上半轮廓似乎并不好求。然而将该图形的一些线段进行平移后(如下图),我们可以惊奇地发现,求“楼梯的上半轮廓”,其实就是求长方形的周长的一半。
平移后得出的长方形的长为“每阶宽度×8阶”,即 )(厘米),宽为“每阶高度×8阶”,即 (厘米)。故而长方形的周长为( 8(厘米)。然而我们要求的是工作人员经过的路程,即楼梯的上半轮廓部分,也就是长方形周长的一半,所以要除以2。
解:将舞台的部分线段平移后,可得长方形如下:
长:25×8=200(厘米),宽:18×8=144(厘米),(200+144)×2÷2=344(厘米)。
答:工作人员经过的距离为344厘米。
思维训练1
1.已知下图所示图形是由8个边长为7分米的正方形拼接而成,求其周长。
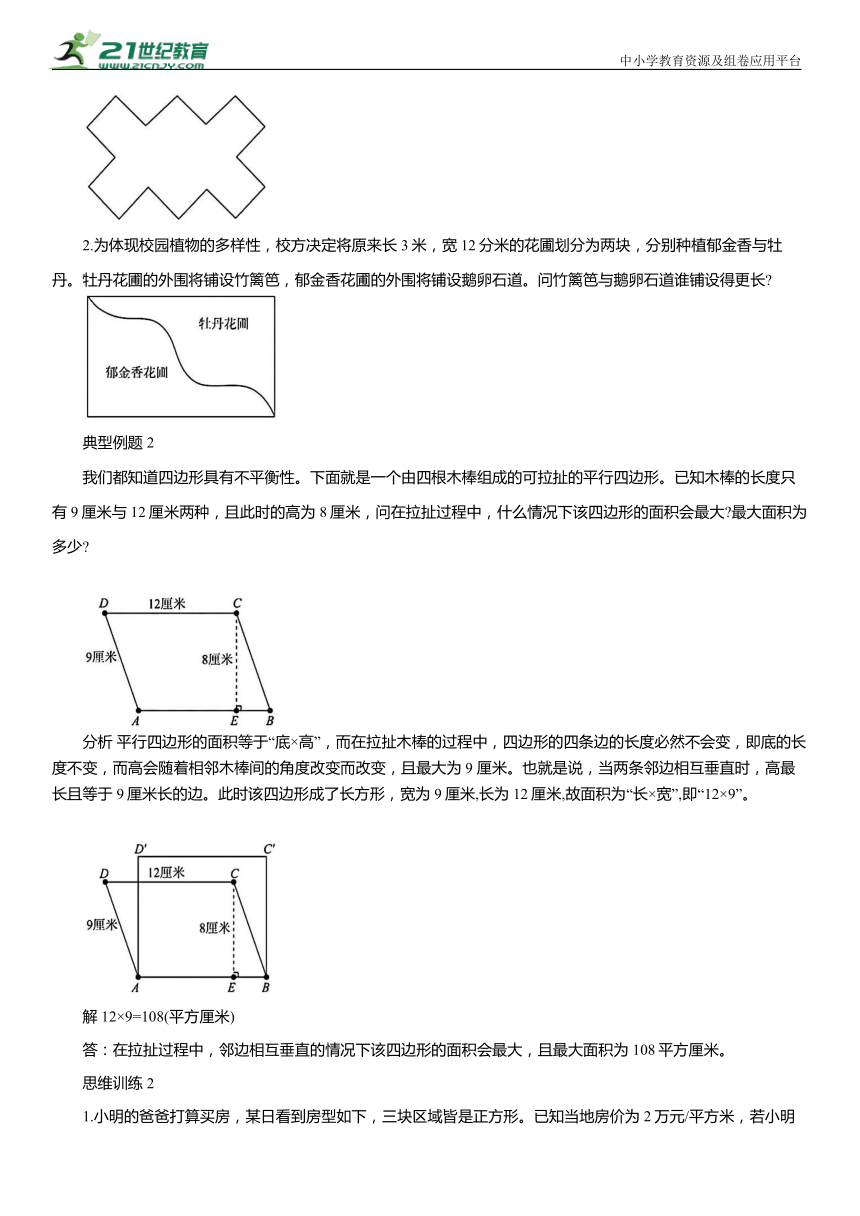
2.为体现校园植物的多样性,校方决定将原来长3米,宽12分米的花圃划分为两块,分别种植郁金香与牡丹。牡丹花圃的外围将铺设竹篱笆,郁金香花圃的外围将铺设鹅卵石道。问竹篱笆与鹅卵石道谁铺设得更长
典型例题2
我们都知道四边形具有不平衡性。下面就是一个由四根木棒组成的可拉扯的平行四边形。已知木棒的长度只有9厘米与12厘米两种,且此时的高为8厘米,问在拉扯过程中,什么情况下该四边形的面积会最大 最大面积为多少
分析 平行四边形的面积等于“底×高”,而在拉扯木棒的过程中,四边形的四条边的长度必然不会变,即底的长度不变,而高会随着相邻木棒间的角度改变而改变,且最大为9 厘米。也就是说,当两条邻边相互垂直时,高最长且等于9厘米长的边。此时该四边形成了长方形,宽为9厘米,长为12厘米,故面积为“长×宽”,即“12×9”。
解 12×9=108(平方厘米)
答:在拉扯过程中,邻边相互垂直的情况下该四边形的面积会最大,且最大面积为 108平方厘米。
思维训练2
1.小明的爸爸打算买房,某日看到房型如下,三块区域皆是正方形。已知当地房价为2万元/平方米,若小明家要买这套房需要准备多少钱
2.某长方形木板的周长为42厘米,在该木板上裁去面积最大的正方形后,留下的长方形的宽为5厘米,求裁去的正方形面积。
典型例题3
某长方形土地长为4 米,宽为3米,中央有一边长为30分米的正方形区域不可种植;两侧各有一个上底为20厘米,下底为40厘米,高为50厘米的梯形区域不可种植。求可种植区域的面积。
分析 根据题目,我们可以分析出该土地的情况应如图:
从图中可知,只要将大长方形面积减去正方形面积和两个梯形的面积,就能求得可种植区域的面积。
首先,长方形面积为“4×3=12”平方米,正方形面积为“30×30=900”平方分米,两个梯形面积为 平方厘米。
接着,我们利用单位利率进行单位之间的换算,将面积单位统一起来。由于涉及平方米、平方分米、平方厘米三种面积单位,故而在这里我们将选取平方分米作为最终结果。
12平方米=1200平方分米;3000平方厘米=30 平方分米,即长方形的面积为1200平方分米,两个梯形的面积为30平方分米。
最后,将长方形面积减去正方形面积的差减去两个梯形面积就能求得可种植区域的面积为“1200—900—30=270”平方分米。
解 长方形面积:4×3=12(平方米)=1200(平方分米),
正方形面积:30×30=900(平方分米),
两个梯形面积: ×(20+40)×50×2=3000(平方厘米)=30(平方分米),
可种植区域的面积:1200—900—30=270(平方分米)。
答:可种植区域的面积为 270平方分米。
思维训练3
1.某长方形土地长为11米,宽为7米,中央有一边长为60分米的正方形区域不可种植。经过技术开发后,在该正方形区域中心又有一个边长为40厘米的正方形区域并且该正方形区域四边上各有一个上底为25厘米,下底为45 厘米,高为80厘米的梯形区域可种植。求可种植区域的面积。
一个长方形,周长为3米,长是宽的3倍多30厘米,则这个长方形的面积为多少平方分米
典型例题4
某长方形长宽比为5:3,已知其周长为48,求其面积。
分析 因为长方形的周长=(长+宽)×2,所以“长+宽”等于‘ 因为某长方形的长宽比为5:3,也就是说“长+宽”一共分成了“5+3=8”份,每一份是 所以长为“5×3=15”,宽为“3×3=9”。因为长方形的面积=长×宽,所以长方形的面积等于15×9=135。
解 5+3=8,48÷2÷8=3,
长:5×3=15,宽:3×3=9,面积:15×9=135。
答:面积为135。
思维训练4
1.某长方形菜圃长宽比为7:2,已知其宽为4米,求菜圃面积。
2.某正方形木板的一边长减少了3厘米,则整体面积减少了 42平方厘米,求原来正方形的边长。
竞赛强化
1.两个 的三角形一定能拼成一个平行四边形。
2.一个正方形,相邻的两条边长度之和是3分米,则这个正方形的面积为 平方厘米。
3.一个梯形的下底是上底的5倍,如果把下底缩小12厘米,那么梯形就变成了一个平行四边形。则原来的梯形的上底是 厘米,下底是 厘米。
4.以下说法正确的有 。
① 把一个长方形框架沿着对角拉成平行四边形时,平行四边形的面积与原来长方形的面积相比变小;
② 经过平行四边形的中心点任意画一条直线,都能把这个平行四边形分成两个完全一样的图形,那么这两个图形一定是三角形;
③有一组对边平行的四边形是平行四边形;
④捏住一个用木条钉成的平行四边形的对角,将平行四边形拉成一个长方形,它的面积变小了。
5.把两个边长分别为10 厘米,4厘米,7 厘米的三角形,拼成一个平行四边形,共有 种拼法,其中周长最大的平行四边形的周长是 厘米。
6.用六个边长为6厘米的小正方形拼成一个长方形,这个长方形的周长是多少厘米
7.小明的爸爸打算买房,某日看到房型如下,中间区域是正方形,两边是长方形。已知当地房价为2万元/平方米,若小明家要买这套房需要准备多少钱
8.下图所示图形是由若干个正方形拼接而成,已知该图形的周长为192厘米,求其面积。
9.在下边画出三种由两个边分别为2厘米,3厘米,4厘米的三角形拼成的平行四边形。(每个格子边长为1厘米)
一个长方形,周长为14分米,长是宽的2倍少5厘米,求这个长方形的面积。
11.为了给外婆过生日,小贺一家分成两组出发。妈妈先后经过蛋糕店和超市,最后到达外婆家,同时小贺和爸爸也从家里出发,经过鲜花店,最后与妈妈同时到达外婆家。已知小贺和爸爸的行走速度是妈妈的 ,超市距外婆家仅15米,问小贺一家一共走了多少米
第 3 讲 四边形
中小学教育资源及组卷应用平台
思维训练1
1.将该图形中的部分线段平移后可得:边长为“7 分米×4”的正方形,如下图。
7×4×4=112(分米)。答:周长为112分米。
2.原来花圃为长方形,故而割据后,牡丹花圃的周长与郁金香花圃的周长皆是“长+宽+公共曲线”。所以两个图形的周长一样长,即竹篱巴与鹅卵石道铺设得一样长。
思维训练2
1. 房子面积:9×9+5×5+4×4=122(平方米),122×2=244(万元)。答:小明家要买这套房需准备244万元。
2. 解法一:42÷2=21(厘米),正方形的边长:(21——5)÷2=8(厘米),正方形的面积:8×8=64(平方厘米)。
解法二:5×2=10(厘米),正方形的边长:(42—10)÷4=8(厘米),正方形的面积:8×8=64(平方厘米)。
答:裁去的正方形的面积为64平方厘米。
思维训练3
1.根据题意可知土地情况如下图,故而可参照典型例题3中的解析作答。
长方形面积:7×11=77(平方米)=7700(平方分米),大正方形面积:60×60=3600(平方分米),四个梯形面积: (25+45)×80×4=11200(平方厘米)=112(平方分米),小正方形面积:40×40=1600(平方厘米)=16(平方分米),可种植区域的面积:7700—3600+112+16=4228(平方分米)。答:可种植区域的面积为4228平方分米。
2.本题的关键点在于数据的单位不统一。首先将单位进行转换:3米=30 分米,30厘米=3分米。再来,已知周长为 30分米,也就是知道“长+宽”等于“30÷2=15”分米。又知“长是宽的 3 倍多 3 分米”,故而可作辅助线段图如下。
故而,我们将长与宽的和——“15 分米”——减去多出的“3分米”,剩下的部分就成了“3+1=4”份,也就是说 4倍的宽等于“15——3——12”分米,所以长方形的
宽等于“12÷4=3”分米,长方形的长等于“3×3+3=12”分米。所以长方形的面积等于“12×3=36”平方分米。
思维训练4
1. 长:4÷2×7=14(米),面积:14×4=56(平方米)。答:菜圃面积为56平方米。
2.如图,由于减少了 3 厘米长的边长,随之减去的面积部分为长与原正方形边长相等的长方形。故而将该面积除以宽,就能得出正方形边长。
42÷3=14(厘米)。答:原来正方形的边长为14厘米。
竞赛强化
1.完全相同。提示:两个完全相同的三角形一定能拼成一个平行四边形。
2. 225。提示:首先要统一单位,3分米=30厘米。正方形的四边相等,所以正方形的边长为30÷2=15厘米,所以正方形的面积为15×15=225平方厘米。
3.3,15。提示:梯形的下底是上底的5倍,所以上底为1倍,下底和上底相差4 倍。如果把下底缩小12厘米,那么梯形就变成了一个平行四边形,而平行四边形的对边相等。换而言之,上底的4倍是12厘米。所以上底为 12÷4=3厘米,下底为3×5=15厘米。
4.①。提示:①平行四边形的面积等于“底×高”,而在拉扯木棒的过程中,四边形的四条边的长度必然不会变,即底的长度不变,而高会随着相邻木棒间的角度改变而改变,而当两条邻边相互垂直时,高最长且等于邻边,换而言之,当对边相等时,成为长方形时面积最大。所以对;②经过平行四边形的中心点任意画一条直线,也有可能将它分为相同的梯形,所以错;③有两组对边分别平行的四边形是平行四边形,只有一组对边平行的四边形是梯形,所以错;④将平行四边形拉成一个长方形,它的面积将变大,所以错。
5. 3,34。提示:将三角形的10厘米,4厘米,7 厘米分别重合,拼起,共有3种拼法。而拼成的平行四边形的周长等于两个三角形的周长和减去重合的两条边。所以要使平行四边形的面积最大,需使减去的重合边最短,即重合边为4 厘米。2×(10+4+7)—2×4=34(厘米)。
6.(1)当小正方形的组合方式如下图时,则
长方形的宽:6×1=6(厘米),长方形的长:6×6=36(厘米),长方形的周长:(6+36)×2=84(厘米)。
(2)当小正方形的组合方式如下图时,则
长方形的宽:6×2=12(厘米),长方形的长:6×3=18(厘米),长方形的周长:(12+18)×2=60(厘米)。
答:长方形的周长为84厘米或60厘米。
7. 8×8+2×4+5×6=102(平方米),102×2=204(万元)。答:需要准备240万元。
8. 192÷4÷4=12(厘米),12×12×8=1152(平方厘米)。答:其面积为 1152 平方厘米。
9.略(以2厘米、3厘米、4厘米为重合的边,皆能拼出平行四边形)。
10. 14分米=140厘米,长方形的宽:140÷2+5=75(厘米),75÷3=25(厘米),长方形的长:25×2—5=45(厘米),长方形的面积:25×45=1125(平方厘米)。答:长方形的面积为 1125 平方厘米。
11.这道题与思维训练3中的第2题有异曲同工之妙。虽然题目中,提供的是爸爸与妈妈的运动速度关系,但是他们的运动时间是相同的。根据“路程=速度×时间”,我们可以知道这个速度关系与路程关系是相同的。因为“小贺和爸爸的行走速度是妈妈的 ”,所以“小贺和爸爸的行走路程是妈妈的 ”,即,若是将妈妈的路程平均分成21份,爸爸他们的路程就相当于其中的 20 份。具体如下图:
从以上两图中我们可以看到,妈妈比爸爸多走了“21份”中的1份。而这一份,就是去外婆家中的多走的部分——共有两段,一段是“超市→外婆家”,还有一段是“小贺家→蛋糕店”中同“超市→外婆家”一样长的路段,即妈妈多走了“15×2=30”米。所以“21份”中的1份就是30米。而爸爸和妈妈一共走了“20+21=41”份这样的路段,所以一家人一共行走“41×30=1230”米。
专题概述
生活中,常常能看到有四条边、四个角的封闭图形,我们称之为四边形。在四边形当中还含有几种特殊的四边形——梯形、平行四边形、长方形和正方形。
梯形:只有一组对边平行的四边形。梯形中平行的一组对边分别叫“上底”和“下底”,不平行的一组对边皆叫“腰”。过梯形的一顶点,作该顶点所对应的边的垂线。我们称这条垂线为“高”,与之垂直的边为“底”。
梯形的面积=(上底+下底)×高÷2。
平行四边形:两组对边分别平行的四边形。平行四边形的对边平行且相等,对角也相等。相较于三角形的稳定性而言,平行四边形具有不稳定性。过平行四边形的一顶点,作该顶点所对应的边的垂线。我们称这条垂线为“高”,与之垂直的边为“底”。
平行四边形的面积=底×高。由公式可知,同底等高的平行四边形面积相等。
长方形:有一个角是直角的平行四边形。长方形是特殊的平行四边形,它不仅具有平行四边形所具有的所有性质,它的四个角还都为直角。我们一般称长方形中较长的那一条边为“长”,较短的那一条边为“宽”。
长方形的周长=(长+宽)×2;长方形的面积=长×宽。
正方形:一组邻边相等的长方形。正方形是特殊的长方形,在对边平行且相等,四个角都为直角的基础上,它的四条边都相等,我们一般称正方形的边为“边长”。
正方形的周长=边长×4;正方形的面积=边长×边长。
以上几种图形的关系可以用下图表示。
常用的面积单位有平方厘米( 平方分米 和平方米 相邻两个常用的面积单位之间的进率是100,即:
1平方分米=100平方厘米,
1平方米=100平方分米。
典型例题1
为庆祝“一带一路”国际合作高峰论坛在京顺利召开,某校决定举办一次文艺晚会。在搭设舞台之际,工作人员发现自己将工具包忘在舞台下,故而决定去拿。已知下舞台的楼梯共有8阶,每阶高度为18 厘米,宽度为25厘米(具体如下图所示),请问工作人员经过的距离有多长
分析 根据题干与图形我们可以发现,求“工作人员经过的距离”实际上就是求“楼梯的上半轮廓”。看起来,楼梯上半轮廓似乎并不好求。然而将该图形的一些线段进行平移后(如下图),我们可以惊奇地发现,求“楼梯的上半轮廓”,其实就是求长方形的周长的一半。
平移后得出的长方形的长为“每阶宽度×8阶”,即 )(厘米),宽为“每阶高度×8阶”,即 (厘米)。故而长方形的周长为( 8(厘米)。然而我们要求的是工作人员经过的路程,即楼梯的上半轮廓部分,也就是长方形周长的一半,所以要除以2。
解:将舞台的部分线段平移后,可得长方形如下:
长:25×8=200(厘米),宽:18×8=144(厘米),(200+144)×2÷2=344(厘米)。
答:工作人员经过的距离为344厘米。
思维训练1
1.已知下图所示图形是由8个边长为7分米的正方形拼接而成,求其周长。
2.为体现校园植物的多样性,校方决定将原来长3米,宽12分米的花圃划分为两块,分别种植郁金香与牡丹。牡丹花圃的外围将铺设竹篱笆,郁金香花圃的外围将铺设鹅卵石道。问竹篱笆与鹅卵石道谁铺设得更长
典型例题2
我们都知道四边形具有不平衡性。下面就是一个由四根木棒组成的可拉扯的平行四边形。已知木棒的长度只有9厘米与12厘米两种,且此时的高为8厘米,问在拉扯过程中,什么情况下该四边形的面积会最大 最大面积为多少
分析 平行四边形的面积等于“底×高”,而在拉扯木棒的过程中,四边形的四条边的长度必然不会变,即底的长度不变,而高会随着相邻木棒间的角度改变而改变,且最大为9 厘米。也就是说,当两条邻边相互垂直时,高最长且等于9厘米长的边。此时该四边形成了长方形,宽为9厘米,长为12厘米,故面积为“长×宽”,即“12×9”。
解 12×9=108(平方厘米)
答:在拉扯过程中,邻边相互垂直的情况下该四边形的面积会最大,且最大面积为 108平方厘米。
思维训练2
1.小明的爸爸打算买房,某日看到房型如下,三块区域皆是正方形。已知当地房价为2万元/平方米,若小明家要买这套房需要准备多少钱
2.某长方形木板的周长为42厘米,在该木板上裁去面积最大的正方形后,留下的长方形的宽为5厘米,求裁去的正方形面积。
典型例题3
某长方形土地长为4 米,宽为3米,中央有一边长为30分米的正方形区域不可种植;两侧各有一个上底为20厘米,下底为40厘米,高为50厘米的梯形区域不可种植。求可种植区域的面积。
分析 根据题目,我们可以分析出该土地的情况应如图:
从图中可知,只要将大长方形面积减去正方形面积和两个梯形的面积,就能求得可种植区域的面积。
首先,长方形面积为“4×3=12”平方米,正方形面积为“30×30=900”平方分米,两个梯形面积为 平方厘米。
接着,我们利用单位利率进行单位之间的换算,将面积单位统一起来。由于涉及平方米、平方分米、平方厘米三种面积单位,故而在这里我们将选取平方分米作为最终结果。
12平方米=1200平方分米;3000平方厘米=30 平方分米,即长方形的面积为1200平方分米,两个梯形的面积为30平方分米。
最后,将长方形面积减去正方形面积的差减去两个梯形面积就能求得可种植区域的面积为“1200—900—30=270”平方分米。
解 长方形面积:4×3=12(平方米)=1200(平方分米),
正方形面积:30×30=900(平方分米),
两个梯形面积: ×(20+40)×50×2=3000(平方厘米)=30(平方分米),
可种植区域的面积:1200—900—30=270(平方分米)。
答:可种植区域的面积为 270平方分米。
思维训练3
1.某长方形土地长为11米,宽为7米,中央有一边长为60分米的正方形区域不可种植。经过技术开发后,在该正方形区域中心又有一个边长为40厘米的正方形区域并且该正方形区域四边上各有一个上底为25厘米,下底为45 厘米,高为80厘米的梯形区域可种植。求可种植区域的面积。
一个长方形,周长为3米,长是宽的3倍多30厘米,则这个长方形的面积为多少平方分米
典型例题4
某长方形长宽比为5:3,已知其周长为48,求其面积。
分析 因为长方形的周长=(长+宽)×2,所以“长+宽”等于‘ 因为某长方形的长宽比为5:3,也就是说“长+宽”一共分成了“5+3=8”份,每一份是 所以长为“5×3=15”,宽为“3×3=9”。因为长方形的面积=长×宽,所以长方形的面积等于15×9=135。
解 5+3=8,48÷2÷8=3,
长:5×3=15,宽:3×3=9,面积:15×9=135。
答:面积为135。
思维训练4
1.某长方形菜圃长宽比为7:2,已知其宽为4米,求菜圃面积。
2.某正方形木板的一边长减少了3厘米,则整体面积减少了 42平方厘米,求原来正方形的边长。
竞赛强化
1.两个 的三角形一定能拼成一个平行四边形。
2.一个正方形,相邻的两条边长度之和是3分米,则这个正方形的面积为 平方厘米。
3.一个梯形的下底是上底的5倍,如果把下底缩小12厘米,那么梯形就变成了一个平行四边形。则原来的梯形的上底是 厘米,下底是 厘米。
4.以下说法正确的有 。
① 把一个长方形框架沿着对角拉成平行四边形时,平行四边形的面积与原来长方形的面积相比变小;
② 经过平行四边形的中心点任意画一条直线,都能把这个平行四边形分成两个完全一样的图形,那么这两个图形一定是三角形;
③有一组对边平行的四边形是平行四边形;
④捏住一个用木条钉成的平行四边形的对角,将平行四边形拉成一个长方形,它的面积变小了。
5.把两个边长分别为10 厘米,4厘米,7 厘米的三角形,拼成一个平行四边形,共有 种拼法,其中周长最大的平行四边形的周长是 厘米。
6.用六个边长为6厘米的小正方形拼成一个长方形,这个长方形的周长是多少厘米
7.小明的爸爸打算买房,某日看到房型如下,中间区域是正方形,两边是长方形。已知当地房价为2万元/平方米,若小明家要买这套房需要准备多少钱
8.下图所示图形是由若干个正方形拼接而成,已知该图形的周长为192厘米,求其面积。
9.在下边画出三种由两个边分别为2厘米,3厘米,4厘米的三角形拼成的平行四边形。(每个格子边长为1厘米)
一个长方形,周长为14分米,长是宽的2倍少5厘米,求这个长方形的面积。
11.为了给外婆过生日,小贺一家分成两组出发。妈妈先后经过蛋糕店和超市,最后到达外婆家,同时小贺和爸爸也从家里出发,经过鲜花店,最后与妈妈同时到达外婆家。已知小贺和爸爸的行走速度是妈妈的 ,超市距外婆家仅15米,问小贺一家一共走了多少米
第 3 讲 四边形
中小学教育资源及组卷应用平台
思维训练1
1.将该图形中的部分线段平移后可得:边长为“7 分米×4”的正方形,如下图。
7×4×4=112(分米)。答:周长为112分米。
2.原来花圃为长方形,故而割据后,牡丹花圃的周长与郁金香花圃的周长皆是“长+宽+公共曲线”。所以两个图形的周长一样长,即竹篱巴与鹅卵石道铺设得一样长。
思维训练2
1. 房子面积:9×9+5×5+4×4=122(平方米),122×2=244(万元)。答:小明家要买这套房需准备244万元。
2. 解法一:42÷2=21(厘米),正方形的边长:(21——5)÷2=8(厘米),正方形的面积:8×8=64(平方厘米)。
解法二:5×2=10(厘米),正方形的边长:(42—10)÷4=8(厘米),正方形的面积:8×8=64(平方厘米)。
答:裁去的正方形的面积为64平方厘米。
思维训练3
1.根据题意可知土地情况如下图,故而可参照典型例题3中的解析作答。
长方形面积:7×11=77(平方米)=7700(平方分米),大正方形面积:60×60=3600(平方分米),四个梯形面积: (25+45)×80×4=11200(平方厘米)=112(平方分米),小正方形面积:40×40=1600(平方厘米)=16(平方分米),可种植区域的面积:7700—3600+112+16=4228(平方分米)。答:可种植区域的面积为4228平方分米。
2.本题的关键点在于数据的单位不统一。首先将单位进行转换:3米=30 分米,30厘米=3分米。再来,已知周长为 30分米,也就是知道“长+宽”等于“30÷2=15”分米。又知“长是宽的 3 倍多 3 分米”,故而可作辅助线段图如下。
故而,我们将长与宽的和——“15 分米”——减去多出的“3分米”,剩下的部分就成了“3+1=4”份,也就是说 4倍的宽等于“15——3——12”分米,所以长方形的
宽等于“12÷4=3”分米,长方形的长等于“3×3+3=12”分米。所以长方形的面积等于“12×3=36”平方分米。
思维训练4
1. 长:4÷2×7=14(米),面积:14×4=56(平方米)。答:菜圃面积为56平方米。
2.如图,由于减少了 3 厘米长的边长,随之减去的面积部分为长与原正方形边长相等的长方形。故而将该面积除以宽,就能得出正方形边长。
42÷3=14(厘米)。答:原来正方形的边长为14厘米。
竞赛强化
1.完全相同。提示:两个完全相同的三角形一定能拼成一个平行四边形。
2. 225。提示:首先要统一单位,3分米=30厘米。正方形的四边相等,所以正方形的边长为30÷2=15厘米,所以正方形的面积为15×15=225平方厘米。
3.3,15。提示:梯形的下底是上底的5倍,所以上底为1倍,下底和上底相差4 倍。如果把下底缩小12厘米,那么梯形就变成了一个平行四边形,而平行四边形的对边相等。换而言之,上底的4倍是12厘米。所以上底为 12÷4=3厘米,下底为3×5=15厘米。
4.①。提示:①平行四边形的面积等于“底×高”,而在拉扯木棒的过程中,四边形的四条边的长度必然不会变,即底的长度不变,而高会随着相邻木棒间的角度改变而改变,而当两条邻边相互垂直时,高最长且等于邻边,换而言之,当对边相等时,成为长方形时面积最大。所以对;②经过平行四边形的中心点任意画一条直线,也有可能将它分为相同的梯形,所以错;③有两组对边分别平行的四边形是平行四边形,只有一组对边平行的四边形是梯形,所以错;④将平行四边形拉成一个长方形,它的面积将变大,所以错。
5. 3,34。提示:将三角形的10厘米,4厘米,7 厘米分别重合,拼起,共有3种拼法。而拼成的平行四边形的周长等于两个三角形的周长和减去重合的两条边。所以要使平行四边形的面积最大,需使减去的重合边最短,即重合边为4 厘米。2×(10+4+7)—2×4=34(厘米)。
6.(1)当小正方形的组合方式如下图时,则
长方形的宽:6×1=6(厘米),长方形的长:6×6=36(厘米),长方形的周长:(6+36)×2=84(厘米)。
(2)当小正方形的组合方式如下图时,则
长方形的宽:6×2=12(厘米),长方形的长:6×3=18(厘米),长方形的周长:(12+18)×2=60(厘米)。
答:长方形的周长为84厘米或60厘米。
7. 8×8+2×4+5×6=102(平方米),102×2=204(万元)。答:需要准备240万元。
8. 192÷4÷4=12(厘米),12×12×8=1152(平方厘米)。答:其面积为 1152 平方厘米。
9.略(以2厘米、3厘米、4厘米为重合的边,皆能拼出平行四边形)。
10. 14分米=140厘米,长方形的宽:140÷2+5=75(厘米),75÷3=25(厘米),长方形的长:25×2—5=45(厘米),长方形的面积:25×45=1125(平方厘米)。答:长方形的面积为 1125 平方厘米。
11.这道题与思维训练3中的第2题有异曲同工之妙。虽然题目中,提供的是爸爸与妈妈的运动速度关系,但是他们的运动时间是相同的。根据“路程=速度×时间”,我们可以知道这个速度关系与路程关系是相同的。因为“小贺和爸爸的行走速度是妈妈的 ”,所以“小贺和爸爸的行走路程是妈妈的 ”,即,若是将妈妈的路程平均分成21份,爸爸他们的路程就相当于其中的 20 份。具体如下图:
从以上两图中我们可以看到,妈妈比爸爸多走了“21份”中的1份。而这一份,就是去外婆家中的多走的部分——共有两段,一段是“超市→外婆家”,还有一段是“小贺家→蛋糕店”中同“超市→外婆家”一样长的路段,即妈妈多走了“15×2=30”米。所以“21份”中的1份就是30米。而爸爸和妈妈一共走了“20+21=41”份这样的路段,所以一家人一共行走“41×30=1230”米。
