【人教版数学九年级上册同步练习】 24.1.3弧弦圆心角(含答案)
文档属性
| 名称 | 【人教版数学九年级上册同步练习】 24.1.3弧弦圆心角(含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-25 16:26:01 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
【人教版数学九年级上册同步练习】
24.1.3弧弦圆心角
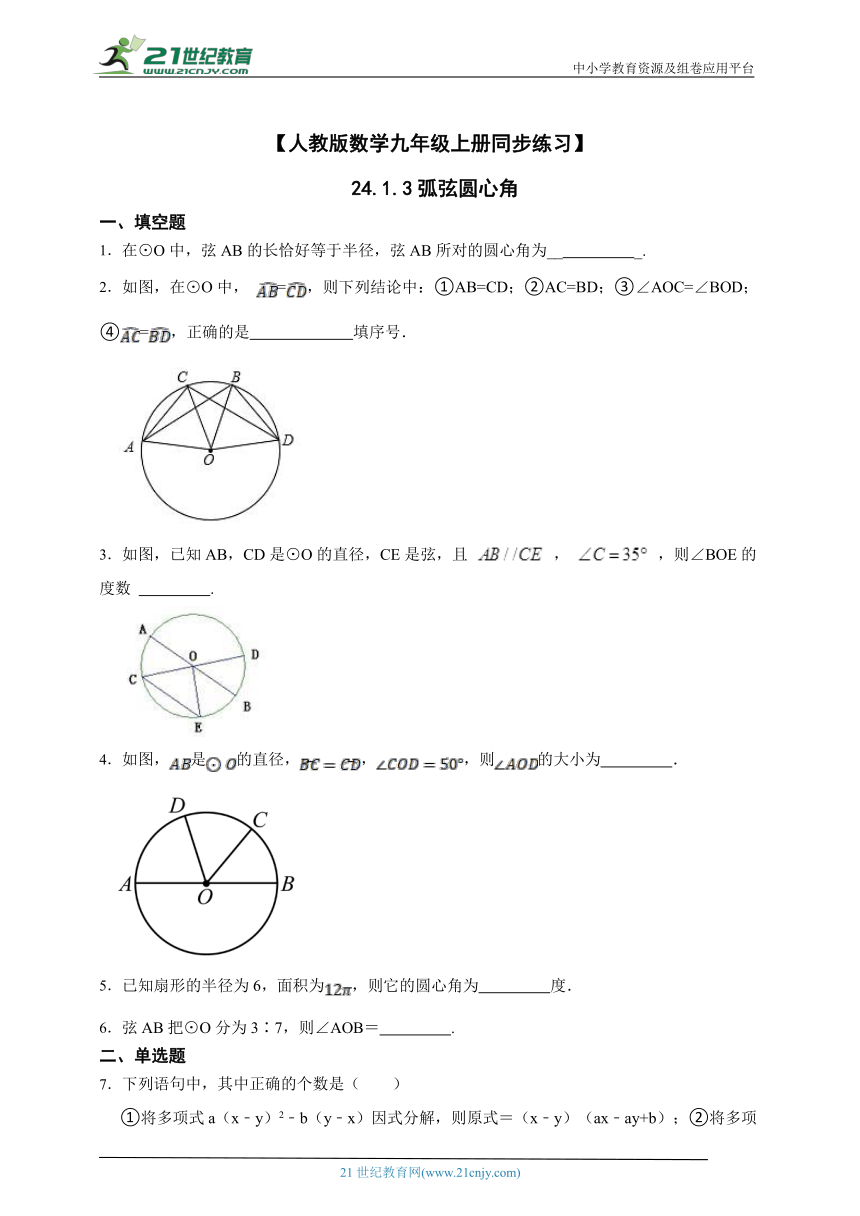
一、填空题
1.在⊙O中,弦AB的长恰好等于半径,弦AB所对的圆心角为__ _.
2.如图,在⊙O中, =,则下列结论中:①AB=CD;②AC=BD;③∠AOC=∠BOD;④=,正确的是 填序号.
3.如图,已知AB,CD是⊙O的直径,CE是弦,且 , ,则∠BOE的度数 .
4.如图,是的直径,,,则的大小为 .
5.已知扇形的半径为6,面积为,则它的圆心角为 度.
6.弦AB把⊙O分为3∶7,则∠AOB= .
二、单选题
7.下列语句中,其中正确的个数是( )
①将多项式a(x﹣y)2﹣b(y﹣x)因式分解,则原式=(x﹣y)(ax﹣ay+b);②将多项式x2+4y2﹣4xy因式分解,则原式=(x﹣2y)2;③90°的圆周角所对的弦是直径;④半圆(或直径)所对的圆周角是直角.
A.1 B.2 C.3 D.4
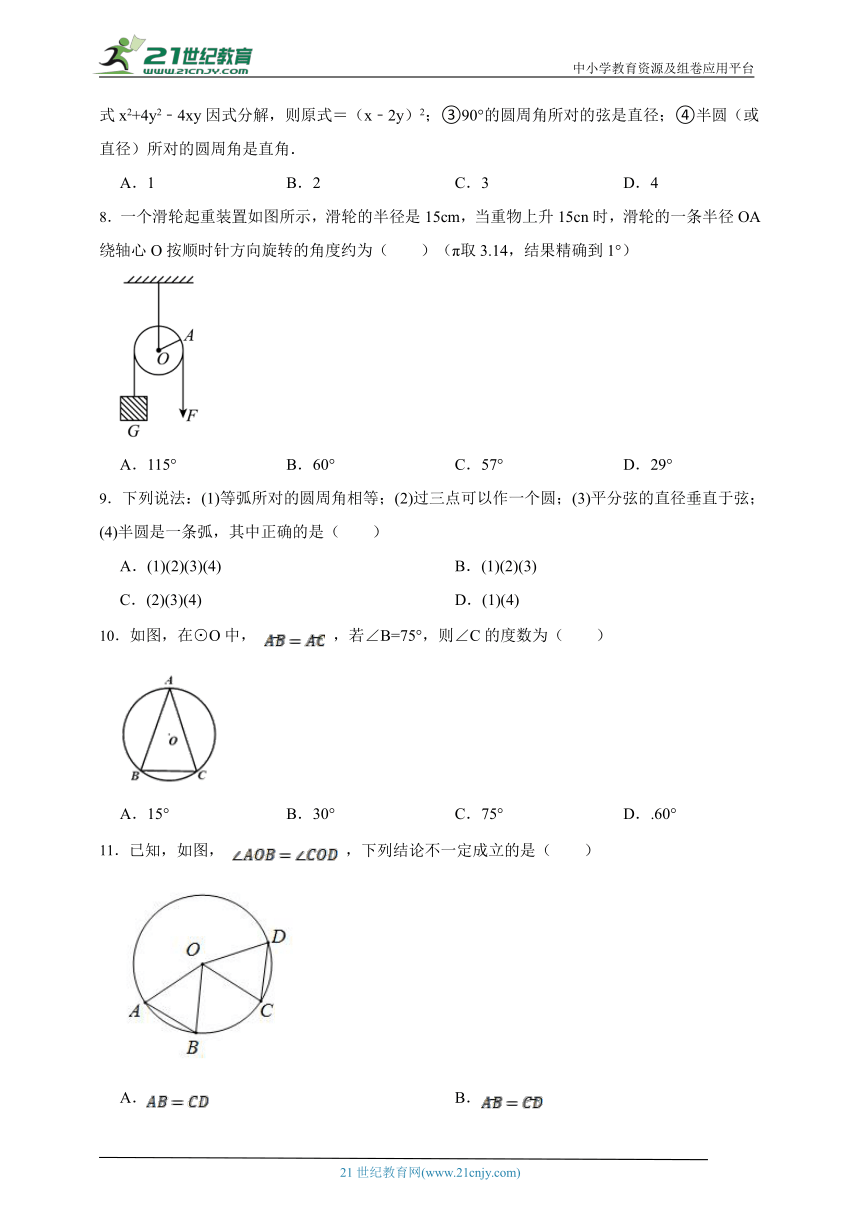
8.一个滑轮起重装置如图所示,滑轮的半径是15cm,当重物上升15cn时,滑轮的一条半径OA绕轴心O按顺时针方向旋转的角度约为( )(π取3.14,结果精确到1°)
A.115° B.60° C.57° D.29°
9.下列说法:(1)等弧所对的圆周角相等;(2)过三点可以作一个圆;(3)平分弦的直径垂直于弦;(4)半圆是一条弧,其中正确的是( )
A.(1)(2)(3)(4) B.(1)(2)(3)
C.(2)(3)(4) D.(1)(4)
10.如图,在⊙O中, ,若∠B=75°,则∠C的度数为( )
A.15° B.30° C.75° D..60°
11.已知,如图, ,下列结论不一定成立的是( )
A. B.
C. D. 都是等边三角形
三、解答题
12.已知:A、B、C、D是⊙O上的四个点,且 ,求证:AC=BD.
如图所示,是圆的一条弦,,垂足为,交圆于点C、D.
13.若,求的度数;
14.若,,求圆的半径长.
四、综合题
15.如图,⊙ 中,弦 与 相交于点E, ,连接 .
求证:
(1) ;
(2) .
答案解析部分
1.【答案】60
【知识点】等边三角形的判定与性质;圆心角、弧、弦的关系
2.【答案】①②③④
【知识点】圆心角、弧、弦的关系
3.【答案】35°
【知识点】圆心角、弧、弦的关系
4.【答案】
【知识点】圆心角、弧、弦的关系
5.【答案】120
【知识点】圆心角、弧、弦的关系
6.【答案】108°
【知识点】圆心角、弧、弦的关系
7.【答案】D
【知识点】实数范围内分解因式;圆心角、弧、弦的关系
8.【答案】C
【知识点】圆心角、弧、弦的关系
9.【答案】D
【知识点】圆的相关概念;圆心角、弧、弦的关系
10.【答案】C
【知识点】等腰三角形的性质;圆心角、弧、弦的关系
11.【答案】D
【知识点】圆心角、弧、弦的关系
12.【答案】证明:∵
∴
∴
【知识点】圆心角、弧、弦的关系
【答案】13.的度数是;
14.圆的半径长为3.
【知识点】勾股定理;垂径定理;圆心角、弧、弦的关系
15.【答案】(1)解:∵AB=CD,
∴ ,即 ,
∴ ;
(2)解:∵ ,
∴AD=BC,
又∵∠ADE=∠CBE,∠DAE=∠BCE,
∴△ADE≌△CBE(ASA),
∴AE=CE.
【知识点】全等三角形的判定与性质;圆心角、弧、弦的关系
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【人教版数学九年级上册同步练习】
24.1.3弧弦圆心角
一、填空题
1.在⊙O中,弦AB的长恰好等于半径,弦AB所对的圆心角为__ _.
2.如图,在⊙O中, =,则下列结论中:①AB=CD;②AC=BD;③∠AOC=∠BOD;④=,正确的是 填序号.
3.如图,已知AB,CD是⊙O的直径,CE是弦,且 , ,则∠BOE的度数 .
4.如图,是的直径,,,则的大小为 .
5.已知扇形的半径为6,面积为,则它的圆心角为 度.
6.弦AB把⊙O分为3∶7,则∠AOB= .
二、单选题
7.下列语句中,其中正确的个数是( )
①将多项式a(x﹣y)2﹣b(y﹣x)因式分解,则原式=(x﹣y)(ax﹣ay+b);②将多项式x2+4y2﹣4xy因式分解,则原式=(x﹣2y)2;③90°的圆周角所对的弦是直径;④半圆(或直径)所对的圆周角是直角.
A.1 B.2 C.3 D.4
8.一个滑轮起重装置如图所示,滑轮的半径是15cm,当重物上升15cn时,滑轮的一条半径OA绕轴心O按顺时针方向旋转的角度约为( )(π取3.14,结果精确到1°)
A.115° B.60° C.57° D.29°
9.下列说法:(1)等弧所对的圆周角相等;(2)过三点可以作一个圆;(3)平分弦的直径垂直于弦;(4)半圆是一条弧,其中正确的是( )
A.(1)(2)(3)(4) B.(1)(2)(3)
C.(2)(3)(4) D.(1)(4)
10.如图,在⊙O中, ,若∠B=75°,则∠C的度数为( )
A.15° B.30° C.75° D..60°
11.已知,如图, ,下列结论不一定成立的是( )
A. B.
C. D. 都是等边三角形
三、解答题
12.已知:A、B、C、D是⊙O上的四个点,且 ,求证:AC=BD.
如图所示,是圆的一条弦,,垂足为,交圆于点C、D.
13.若,求的度数;
14.若,,求圆的半径长.
四、综合题
15.如图,⊙ 中,弦 与 相交于点E, ,连接 .
求证:
(1) ;
(2) .
答案解析部分
1.【答案】60
【知识点】等边三角形的判定与性质;圆心角、弧、弦的关系
2.【答案】①②③④
【知识点】圆心角、弧、弦的关系
3.【答案】35°
【知识点】圆心角、弧、弦的关系
4.【答案】
【知识点】圆心角、弧、弦的关系
5.【答案】120
【知识点】圆心角、弧、弦的关系
6.【答案】108°
【知识点】圆心角、弧、弦的关系
7.【答案】D
【知识点】实数范围内分解因式;圆心角、弧、弦的关系
8.【答案】C
【知识点】圆心角、弧、弦的关系
9.【答案】D
【知识点】圆的相关概念;圆心角、弧、弦的关系
10.【答案】C
【知识点】等腰三角形的性质;圆心角、弧、弦的关系
11.【答案】D
【知识点】圆心角、弧、弦的关系
12.【答案】证明:∵
∴
∴
【知识点】圆心角、弧、弦的关系
【答案】13.的度数是;
14.圆的半径长为3.
【知识点】勾股定理;垂径定理;圆心角、弧、弦的关系
15.【答案】(1)解:∵AB=CD,
∴ ,即 ,
∴ ;
(2)解:∵ ,
∴AD=BC,
又∵∠ADE=∠CBE,∠DAE=∠BCE,
∴△ADE≌△CBE(ASA),
∴AE=CE.
【知识点】全等三角形的判定与性质;圆心角、弧、弦的关系
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
