【人教版数学九年级上册同步练习】 24..1圆的有关性质本节综合题(含答案)
文档属性
| 名称 | 【人教版数学九年级上册同步练习】 24..1圆的有关性质本节综合题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-25 16:25:03 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
【人教版数学九年级上册同步练习】
24..1圆的有关性质
一、填空题
1.在⊙O中,弦AB的长恰好等于半径,弦AB所对的圆心角为__ _.
2.如图1所示,圆形拱门屏风是中国古代家庭中常见的装饰隔断,既美观又实用,彰显出中国元素的韵味.图2是一款拱门的示意图,其中拱门最下端分米,为中点,为拱门最高点,圆心在线段上,分米,则拱门所在圆半径的长为 分米.
3.顶点在 的角叫作圆心角.
4.如图,若 ,则 ,
5.如图,△ABC是⊙O的内接三角形,∠C=40°,连接OA、OB,则∠OAB= °.
6.如图,点A、B、C、D在⊙O上, ,则AC BD(填“>”“<”或“=”)
二、单选题
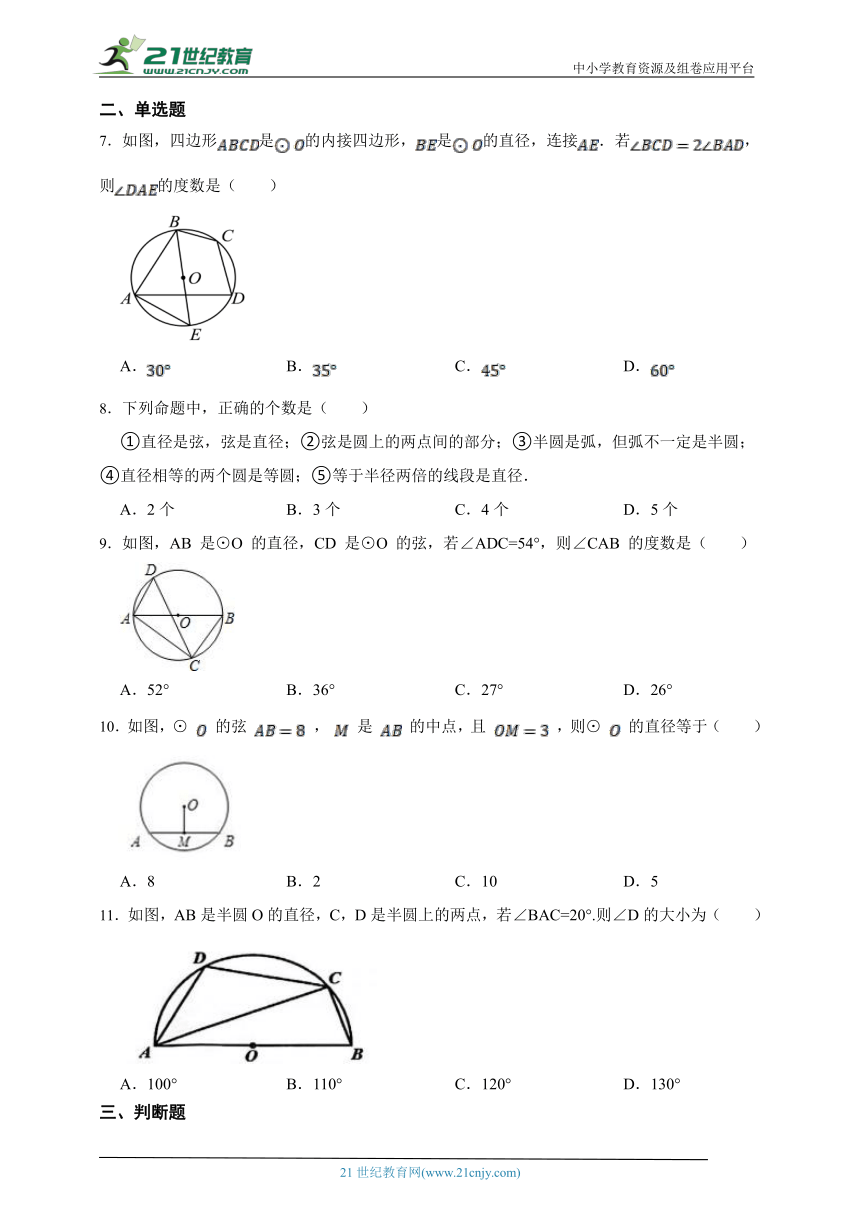
7.如图,四边形是的内接四边形,是的直径,连接.若,则的度数是( )
A. B. C. D.
8.下列命题中,正确的个数是( )
①直径是弦,弦是直径;②弦是圆上的两点间的部分;③半圆是弧,但弧不一定是半圆;④直径相等的两个圆是等圆;⑤等于半径两倍的线段是直径.
A.2个 B.3个 C.4个 D.5个
9.如图,AB 是⊙O 的直径,CD 是⊙O 的弦,若∠ADC=54°,则∠CAB 的度数是( )
A.52° B.36° C.27° D.26°
10.如图,⊙ 的弦 , 是 的中点,且 ,则⊙ 的直径等于( )
A.8 B.2 C.10 D.5
11.如图,AB是半圆O的直径,C,D是半圆上的两点,若∠BAC=20°.则∠D的大小为( )
A.100° B.110° C.120° D.130°
三、判断题
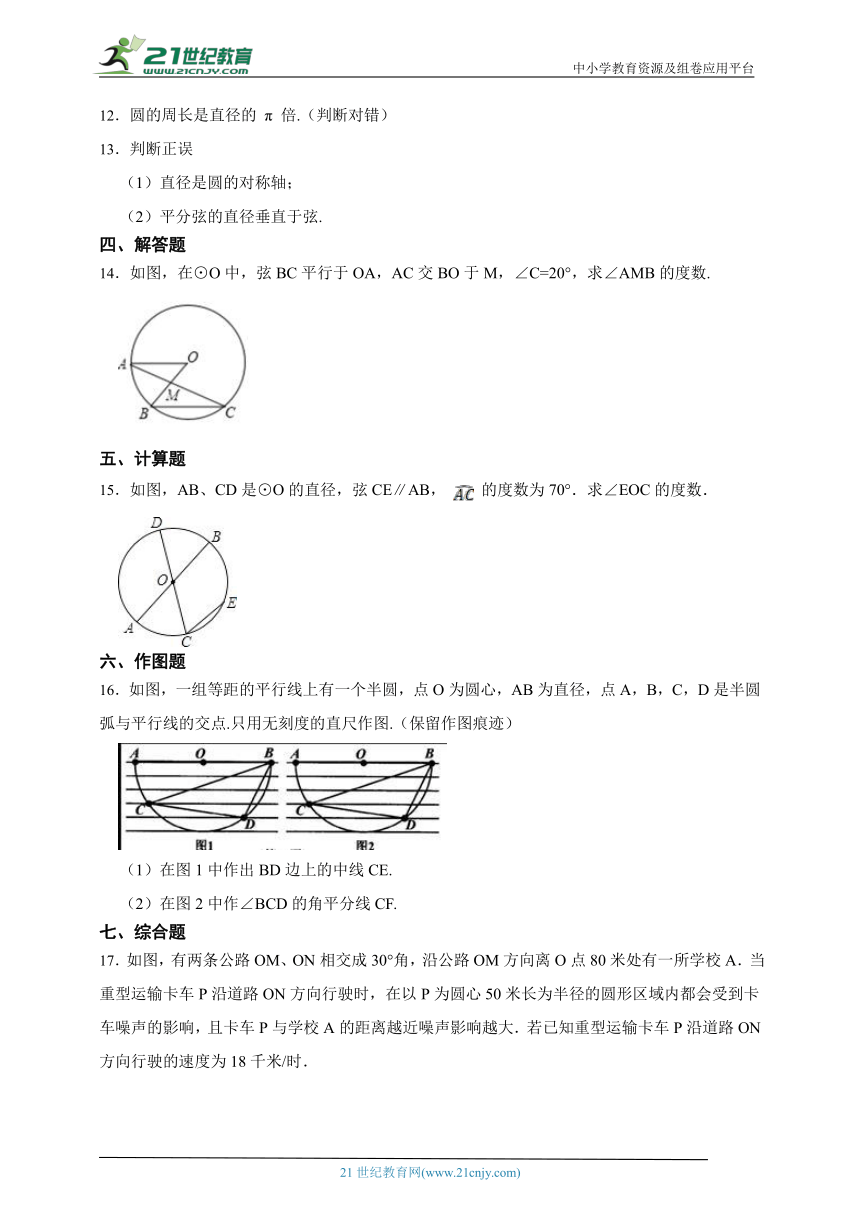
12.圆的周长是直径的 π 倍.(判断对错)
13.判断正误
(1)直径是圆的对称轴;
(2)平分弦的直径垂直于弦.
四、解答题
14.如图,在⊙O中,弦BC平行于OA,AC交BO于M,∠C=20°,求∠AMB的度数.
五、计算题
15.如图,AB、CD是⊙O的直径,弦CE∥AB, 的度数为70°.求∠EOC的度数.
六、作图题
16.如图,一组等距的平行线上有一个半圆,点O为圆心,AB为直径,点A,B,C,D是半圆弧与平行线的交点.只用无刻度的直尺作图.(保留作图痕迹)
(1)在图1中作出BD边上的中线CE.
(2)在图2中作∠BCD的角平分线CF.
七、综合题
17.如图,有两条公路OM、ON相交成30°角,沿公路OM方向离O点80米处有一所学校A.当重型运输卡车P沿道路ON方向行驶时,在以P为圆心50米长为半径的圆形区域内都会受到卡车噪声的影响,且卡车P与学校A的距离越近噪声影响越大.若已知重型运输卡车P沿道路ON方向行驶的速度为18千米/时.
(1)求对学校A的噪声影响最大时卡车P与学校A的距离;
(2)求卡车P沿道路ON方向行驶一次给学校A带来噪声影响的时间.
18.如图,⊙ 中,弦 与 相交于点E, ,连接 .
求证:
(1) ;
(2) .
19.已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C,D(如图所示).
(1)求证:AC=BD;
(2)若大圆的半径R=10,小圆的半径r=8,且圆心O到直线AB的距离为6,求AC的长
答案解析部分
1.【答案】60
【知识点】等边三角形的判定与性质;圆心角、弧、弦的关系
2.【答案】15
【知识点】勾股定理;垂径定理的实际应用
3.【答案】圆心
【知识点】圆心角、弧、弦的关系
4.【答案】30°
【知识点】圆周角定理
5.【答案】50
【知识点】圆周角定理;等腰三角形的性质-等边对等角
6.【答案】=
【知识点】圆心角、弧、弦的关系
7.【答案】A
【知识点】圆周角定理;圆内接四边形的性质
8.【答案】A
【知识点】圆的相关概念
9.【答案】B
【知识点】圆周角定理
10.【答案】C
【知识点】垂径定理
11.【答案】B
【知识点】圆周角定理;圆内接四边形的性质
12.【答案】正确
【知识点】圆的相关概念
13.【答案】(1)正确
(2)错误
【知识点】垂径定理
14.【答案】解:∵∠C=20°
∴∠AOB=40°
又∵弦BC∥半径OA
∴∠OAC=∠C=20°
∵∠AMB是△AOM的外角
∴∠AMB=60°.
【知识点】平行线的性质;三角形的外角性质;圆周角定理
15.【答案】解:连接OE,
∵ 的度数为70°,
∴∠AOC=∠BOD=70°,
∵CE∥AB,
∴∠BOD=∠C=70°,
∵OC=OE,
∴∠C=∠E=70°,
∴∠EOC=180°﹣70°﹣70°=40°
【知识点】圆心角、弧、弦的关系
16.【答案】(1)解:过点O作OE⊥BD于点E,连接CE,
即CE就是所求作的线段;
(2)解:过点O作OF⊥BD叫圆O于点F,作射线CF,即CF就是所求作的角平分线.
【知识点】垂径定理;尺规作图-作角的平分线
17.【答案】(1)解:过点A作AD⊥ON于点D,
∵∠NOM=30°,AO=80m,
∴AD=40m,
即对学校A的噪声影响最大时卡车P与学校A的距离为40米;
(2)解:由图可知:以50m为半径画圆,分别交ON于B,C两点,AD⊥BC,BD=CD= BC,OA=80m,
∵在Rt△AOD中,∠AOB=30°,
∴AD= OA= ×80=40m,
在Rt△ABD中,AB=50,AD=40,由勾股定理得:BD= = =30m,
故BC=2×30=60米,即重型运输卡车在经过BC时对学校产生影响.
∵重型运输卡车的速度为18千米/小时,即 =300米/分钟,
∴重型运输卡车经过BC时需要60÷300=0.2(分钟)=12(秒).
答:卡车P沿道路ON方向行驶一次给学校A带来噪声影响的时间为12秒
【知识点】勾股定理的应用;垂径定理的实际应用
18.【答案】(1)解:∵AB=CD,
∴ ,即 ,
∴ ;
(2)解:∵ ,
∴AD=BC,
又∵∠ADE=∠CBE,∠DAE=∠BCE,
∴△ADE≌△CBE(ASA),
∴AE=CE.
【知识点】全等三角形的判定与性质;圆心角、弧、弦的关系
19.【答案】(1)证明:过点O作OE⊥AB于E,
则CE=DE,AE=BE.
∴AE-CE=BE-DE即AC=BD
(2)解:连接OC,OA由(1)可知,OE⊥AB且OE⊥CD,∴OE=6∴CE= AE=
∴AC=AE-CE=8-2
【知识点】勾股定理;垂径定理
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【人教版数学九年级上册同步练习】
24..1圆的有关性质
一、填空题
1.在⊙O中,弦AB的长恰好等于半径,弦AB所对的圆心角为__ _.
2.如图1所示,圆形拱门屏风是中国古代家庭中常见的装饰隔断,既美观又实用,彰显出中国元素的韵味.图2是一款拱门的示意图,其中拱门最下端分米,为中点,为拱门最高点,圆心在线段上,分米,则拱门所在圆半径的长为 分米.
3.顶点在 的角叫作圆心角.
4.如图,若 ,则 ,
5.如图,△ABC是⊙O的内接三角形,∠C=40°,连接OA、OB,则∠OAB= °.
6.如图,点A、B、C、D在⊙O上, ,则AC BD(填“>”“<”或“=”)
二、单选题
7.如图,四边形是的内接四边形,是的直径,连接.若,则的度数是( )
A. B. C. D.
8.下列命题中,正确的个数是( )
①直径是弦,弦是直径;②弦是圆上的两点间的部分;③半圆是弧,但弧不一定是半圆;④直径相等的两个圆是等圆;⑤等于半径两倍的线段是直径.
A.2个 B.3个 C.4个 D.5个
9.如图,AB 是⊙O 的直径,CD 是⊙O 的弦,若∠ADC=54°,则∠CAB 的度数是( )
A.52° B.36° C.27° D.26°
10.如图,⊙ 的弦 , 是 的中点,且 ,则⊙ 的直径等于( )
A.8 B.2 C.10 D.5
11.如图,AB是半圆O的直径,C,D是半圆上的两点,若∠BAC=20°.则∠D的大小为( )
A.100° B.110° C.120° D.130°
三、判断题
12.圆的周长是直径的 π 倍.(判断对错)
13.判断正误
(1)直径是圆的对称轴;
(2)平分弦的直径垂直于弦.
四、解答题
14.如图,在⊙O中,弦BC平行于OA,AC交BO于M,∠C=20°,求∠AMB的度数.
五、计算题
15.如图,AB、CD是⊙O的直径,弦CE∥AB, 的度数为70°.求∠EOC的度数.
六、作图题
16.如图,一组等距的平行线上有一个半圆,点O为圆心,AB为直径,点A,B,C,D是半圆弧与平行线的交点.只用无刻度的直尺作图.(保留作图痕迹)
(1)在图1中作出BD边上的中线CE.
(2)在图2中作∠BCD的角平分线CF.
七、综合题
17.如图,有两条公路OM、ON相交成30°角,沿公路OM方向离O点80米处有一所学校A.当重型运输卡车P沿道路ON方向行驶时,在以P为圆心50米长为半径的圆形区域内都会受到卡车噪声的影响,且卡车P与学校A的距离越近噪声影响越大.若已知重型运输卡车P沿道路ON方向行驶的速度为18千米/时.
(1)求对学校A的噪声影响最大时卡车P与学校A的距离;
(2)求卡车P沿道路ON方向行驶一次给学校A带来噪声影响的时间.
18.如图,⊙ 中,弦 与 相交于点E, ,连接 .
求证:
(1) ;
(2) .
19.已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C,D(如图所示).
(1)求证:AC=BD;
(2)若大圆的半径R=10,小圆的半径r=8,且圆心O到直线AB的距离为6,求AC的长
答案解析部分
1.【答案】60
【知识点】等边三角形的判定与性质;圆心角、弧、弦的关系
2.【答案】15
【知识点】勾股定理;垂径定理的实际应用
3.【答案】圆心
【知识点】圆心角、弧、弦的关系
4.【答案】30°
【知识点】圆周角定理
5.【答案】50
【知识点】圆周角定理;等腰三角形的性质-等边对等角
6.【答案】=
【知识点】圆心角、弧、弦的关系
7.【答案】A
【知识点】圆周角定理;圆内接四边形的性质
8.【答案】A
【知识点】圆的相关概念
9.【答案】B
【知识点】圆周角定理
10.【答案】C
【知识点】垂径定理
11.【答案】B
【知识点】圆周角定理;圆内接四边形的性质
12.【答案】正确
【知识点】圆的相关概念
13.【答案】(1)正确
(2)错误
【知识点】垂径定理
14.【答案】解:∵∠C=20°
∴∠AOB=40°
又∵弦BC∥半径OA
∴∠OAC=∠C=20°
∵∠AMB是△AOM的外角
∴∠AMB=60°.
【知识点】平行线的性质;三角形的外角性质;圆周角定理
15.【答案】解:连接OE,
∵ 的度数为70°,
∴∠AOC=∠BOD=70°,
∵CE∥AB,
∴∠BOD=∠C=70°,
∵OC=OE,
∴∠C=∠E=70°,
∴∠EOC=180°﹣70°﹣70°=40°
【知识点】圆心角、弧、弦的关系
16.【答案】(1)解:过点O作OE⊥BD于点E,连接CE,
即CE就是所求作的线段;
(2)解:过点O作OF⊥BD叫圆O于点F,作射线CF,即CF就是所求作的角平分线.
【知识点】垂径定理;尺规作图-作角的平分线
17.【答案】(1)解:过点A作AD⊥ON于点D,
∵∠NOM=30°,AO=80m,
∴AD=40m,
即对学校A的噪声影响最大时卡车P与学校A的距离为40米;
(2)解:由图可知:以50m为半径画圆,分别交ON于B,C两点,AD⊥BC,BD=CD= BC,OA=80m,
∵在Rt△AOD中,∠AOB=30°,
∴AD= OA= ×80=40m,
在Rt△ABD中,AB=50,AD=40,由勾股定理得:BD= = =30m,
故BC=2×30=60米,即重型运输卡车在经过BC时对学校产生影响.
∵重型运输卡车的速度为18千米/小时,即 =300米/分钟,
∴重型运输卡车经过BC时需要60÷300=0.2(分钟)=12(秒).
答:卡车P沿道路ON方向行驶一次给学校A带来噪声影响的时间为12秒
【知识点】勾股定理的应用;垂径定理的实际应用
18.【答案】(1)解:∵AB=CD,
∴ ,即 ,
∴ ;
(2)解:∵ ,
∴AD=BC,
又∵∠ADE=∠CBE,∠DAE=∠BCE,
∴△ADE≌△CBE(ASA),
∴AE=CE.
【知识点】全等三角形的判定与性质;圆心角、弧、弦的关系
19.【答案】(1)证明:过点O作OE⊥AB于E,
则CE=DE,AE=BE.
∴AE-CE=BE-DE即AC=BD
(2)解:连接OC,OA由(1)可知,OE⊥AB且OE⊥CD,∴OE=6∴CE= AE=
∴AC=AE-CE=8-2
【知识点】勾股定理;垂径定理
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
