选择必修 第一章 1.4.2用空间向量研究距离、夹角问题 第2课时
文档属性
| 名称 | 选择必修 第一章 1.4.2用空间向量研究距离、夹角问题 第2课时 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-09-18 10:34:49 | ||
图片预览








文档简介
(共27张PPT)
选择必修 第一章
1.4.2 用空间向量研究距离、夹角问题
第2课时 空间夹角
人教A版(2019)
教学目标
学习目标 数学素养
1.理解两异面直线所成角与它们的方向向量之间的关系,会用向量方法求两异面直线所成的角. 1.空间直观素养和运算素养.
2.理解直线与平面所成角与直线方向向量和平面法向量夹角之间的关系,会用向量方法求直线与平面所成的角. 2.空间直观素养和运算素养.
3.理解二面角的夹角与两个平面法向量的夹角之间的关系,会用向量方法求二面角的大小. 3.空间直观素养和运算素养.
温故知新
2.点到平面的距离
3.空间距离问题的转化
已知直线l的单位方向向量为,,设,则
.
已知平面α的法向量为,则
.
⑴求两条平行直线间的距离可转化为求其中一条直线上一点到另一条直线的距离.
⑵直线与平面平行,求它们之间的距离,可转化为求这条直线上一点到这个平面的距离.
⑶求两个平行平面间的距离,可转化为求其中一个平面上一点到另一个平面的距离.
1.点到直线的距离
新知探究
与距离类似,角度是立体几何中另一个重要的度量. 下面我们用向量方法研究直线与直线所成角、直线与平面所成角及平面与平面所成角.
【例1】如图,在棱长为1的正四面体(四个面都是正三角形)ABCD中,M,N分别为BC,AD的中点,求直线AM和CN夹角的余弦值.
分析:直线AM和CN夹角的余弦值,可以转化为求向量与夹角的余弦值,为此需要把向量用适当的极点表示出来,进而求得向量夹角的余弦值.
新知探究
解:
化为向量问题
如图,以{}作为基底,则
,
.
设向量与的夹角为θ,则直线AM和CN夹角的余弦值等于|cosθ|.
进行向量运算
.
.
.
又△ABC和△ACD均为等边三角形,
所以.
所以.
回到图形问题
所以直线AM和CN夹角的余弦值为.
新知探究
以上我们用向量方法解决了异面直线AM和CN所成角的问题,你能用向量方法求直线AB与平面BCD所成的角吗?
一般地,两条异面直线所成的角,可以转化为两条异面直线的方向向量的夹角来求得. 也就是说,若异面直线l1,l2所成的角为θ(),其方向向量分别是,则
.
新知探究
类似地,直线与平面所成的角,可以转化为直线的方向向量与平面的法向量的夹角.如图,直线AB与平面α相交于点B.设直线AB与平面α所成的角为θ,直线AB的方向向量为,平面α的法向量为,则
.
新知探究
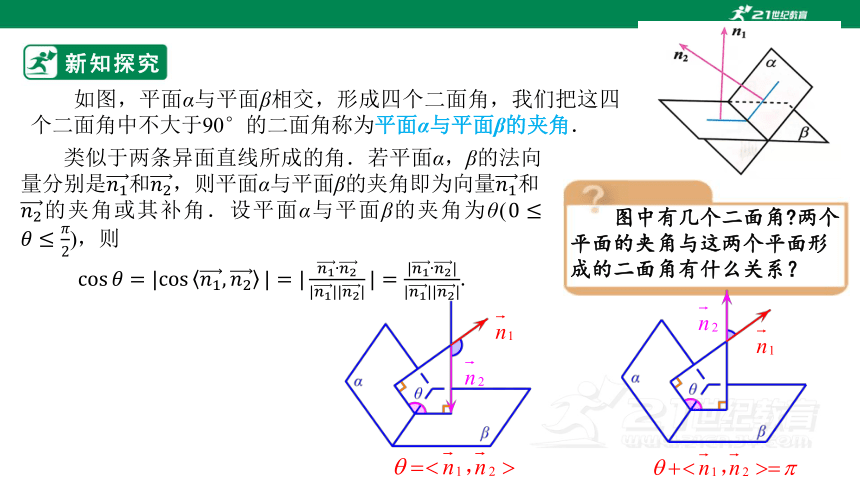
如图,平面α与平面β相交,形成四个二面角,我们把这四个二面角中不大于90°的二面角称为平面α与平面β的夹角.
图中有几个二面角 两个平面的夹角与这两个平面形成的二面角有什么关系?
类似于两条异面直线所成的角.若平面α,β的法向量分别是和,则平面α与平面β的夹角即为向量和
的夹角或其补角.设平面α与平面β的夹角为θ(),则
.
新知探究
解:
以直线BA,BC,BB1分别为x轴,y轴,z轴,建立如图所示的空间直角坐标系.设AB=1,则
∴=(-,0,),=(0,1,1),
∴,
∴直线EF和BC1所成角的大小为.
【例2】如图,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AB=BC=AA1,∠ABC=90°,E,F分别是棱AB,BB1的中点,求直线EF和BC1所成角的大小.
B(0,0,0),E(,0,0),F(0,0,),C1(0,1,1).
新知探究
用向量法求异面直线所成角的一般步骤
⑴选好基底或建立空间直角坐标系;
⑵求出两直线的方向向量;
⑶代入公式求解.
新知探究
【例3】已知正三棱柱ABC-A1B1C1中的底面边长为a,侧棱长为a,M为A1B1的中点,求BC1与平面AMC1所成角的正弦值.
解:
如图,建立空间直角坐标系,则
A(0,0,0),B(0,,a,0),M(0,,),C1(,,),
∴(0,),=(,0,0,),=().
设BC1与平面AMC1所成角为θ,平面AMC1的法向量=(x,y,z),则
,
即,
取z=,则y=-4,x=0,=(0,-4,).
∴.
新知探究
用向量法求线面所成角的步骤
⑴建立恰当的空间直角坐标系.
⑵求直线的方向向量;
⑶求平面的法向量;
⑷计算:设线面角为θ,则.
新知探究
【例4】如图,在直三棱柱ABC-A1B1C1中,AC=CB=2,AA1=3,∠ACB=90°,P为BC的中点,点Q,R分别在棱AA1,BB1上,A1Q=2AQ,BR=2RB1.求平面PQR与平面A1B1C1夹角的余弦值.
解:
因为CC1⊥平面A1B1C1,所以平面A1B1C1的一个法向量
为=(0,0,1).
分析:因为平面PQR与平面A1B1C1夹角可以转化为平面PQR与平面A1B1C1的法向量的夹角,所以只需要求出这两个平面的法向量的夹角即可.
以C1为原点,以C1A1,C1B1,C1C所在直线为x轴,y轴,z轴,建立如图所示的空间直角坐标系.设平面A1B1C1的法向量为,平面PQR的法向量为,则平面PQR与平面A1B1C1的夹角就是与的夹角或其补角.
化为向量问题
进行向量运算
新知探究
【例4】如图,在直三棱柱ABC-A1B1C1中,AC=CB=2,AA1=3,∠ACB=90°,P为BC的中点,点Q,R分别在棱AA1,BB1上,A1Q=2AQ,BR=2RB1.求平面PQR与平面A1B1C1夹角的余弦值.
解:
设=(x,y,z),则
根据建立的空间直角坐标系,可知P(0,1,3),Q(2,0,2),R(0,2,1).
∴=(2,-1,-1),=(0,1,-2).
,
∴,
∴,
取=(3,4,2),则
新知探究
【例4】如图,在直三棱柱ABC-A1B1C1中,AC=CB=2,AA1=3,∠ACB=90°,P为BC的中点,点Q,R分别在棱AA1,BB1上,A1Q=2AQ,BR=2RB1.求平面PQR与平面A1B1C1夹角的余弦值.
解:
回到图形问题
取=(3,4,2),则
.
设平面PQR与平面A1B1C1的夹角为θ,则
.
即平面PQR与平面A1B1C1夹角的余弦值为.
新知探究
用向量法求平面与平面的夹角的步骤
⑴建立空间直角坐标系;
⑵求出两个平面的法向量;
⑶计算:设两个平面的夹角为θ,则.
初试身手
1.如图,在直三棱柱ABC-A1B1C1中,AC=3,BC=4,CC1=3,∠ACB=90°,则BC1与A1C所成的角的余弦值为( )
A. B. C. D.
如图,以C为坐标原点,CA,CB,CC1所在直线分别为x轴,y轴,z轴建立空间直角坐标系,则C(0,0,0),A1(3,0,3),B(0,4,0),C1(0,0,3),
∴(3,0,3),(0,-4,3),
解:
∴BC1与A1C所成的角的余弦值为.故选A.
∴.
A
初试身手
2.四棱锥P-ABCD中,底面为直角梯形,AD//BC,∠BAD=90°,PA⊥平面BACD,PA=AD=AB=2BC=2,M, N分别为PC, PB的中点.
⑴求证:PB⊥DM; ⑵求直线BD和平面ADMN所成角.
解:
如图,以A为原点,分别以AB,AD,AP所在直线为x轴、y轴、z轴建立空间直角坐标系Dxyz,则
A(0,0,0),B(2,0,0),D(0,2,0),P(0,0,2),N(1,01),M(1,,1).
⑵=(-2,2,0),=(0,2,0),=(1,0,1).
∴=0,
∴PB⊥DM.
x
y
z
⑴=(2,0,-2),=(1,,1),
初试身手
2.四棱锥P-ABCD中,底面为直角梯形,AD//BC,∠BAD=90°,PA⊥平面BACD,PA=AD=AB=2BC=2,M, N分别为PC, PB的中点.
⑴求证:PB⊥DM; ⑵求直线BD和平面ADMN所成角.
解:
设平面ADMN的一个法向量=(x,y,z),则
, 即.
⑵=(-2,2,0),=(0,2,0),=(1,0,1).
∴=(1,0,-1),
.
x
y
z
取x=1,则z=-1,
设直线BD和平面ADMN所成角为θ,则
∴θ.
即直线BD和平面ADMN所成角为.
初试身手
解:
⑴在三棱锥P-ABC中,PA⊥底面ABC,∠BAC=90°,故以A为坐标原点,AB,AC,AP所在的直线分别为x轴,y轴,z轴,建立如图所示的空间直角坐标系.
因为D,E,N分别为棱PA,PC,BC的中点,M是线段AD上靠近点A的三等分点,PA=6,AC=4,AB=2,所以M(0,0,1),B(2,0,0),C(0,4,0),N(1,2,0),D(0,0,3),P(0,0,6),E(0,2,3),
∴=(-1,-2,3),=(-2,2,3),
3.如图,在三棱锥P-ABC中,PA⊥底面ABC,∠BAC=90°.D,E,N分别为棱PA,PC,BC的中点,M是线段AD上靠近点A的三等分点,PA=6,AC=4,AB=2.求:
⑴直线ND与直线BE所成角的余弦值;
⑵平面CEM与平面MNE夹角的余弦值.
初试身手
解:
设直线ND与直线BE所成角为θ,则
,
即直线ND与直线BE所成角的余弦值为.
3.如图,在三棱锥P-ABC中,PA⊥底面ABC,∠BAC=90°.D,E,N分别为棱PA,PC,BC的中点,M是线段AD上靠近点A的三等分点,PA=6,AC=4,AB=2.求:
⑴直线ND与直线BE所成角的余弦值;
⑵平面CEM与平面MNE夹角的余弦值.
⑵由⑴得=(1,2,-1),=(0,4,-1),=(0,2,2).
设平面MNE的法向量为=(a,b,c),则
,即,解得,
取c=1,则a=3,b=-1,得=(3,-1,1),
初试身手
解:
易知AB⊥平面CEM,故可设平面CEM的一个法向量为=(1,0,0).
,
设平面CEM与平面MNE的夹角为α,
3.如图,在三棱锥P-ABC中,PA⊥底面ABC,∠BAC=90°.D,E,N分别为棱PA,PC,BC的中点,M是线段AD上靠近点A的三等分点,PA=6,AC=4,AB=2.求:
⑴直线ND与直线BE所成角的余弦值;
⑵平面CEM与平面MNE夹角的余弦值.
即平面CEM与平面MNE夹角的余弦值为
课堂小结
1.用向量法求异面直线所成角
2.用向量法求线面所成角
3.用向量法求平面与平面的夹角
若异面直线l1,l2所成的角为θ(),其方向向量分别是,则
设直线AB与平面α所成的角为θ,直线AB的方向向量为,平面α的法向量为,则
.
.
若平面α,β的法向量分别是和,则平面α与平面β的夹角即为向量和的夹角或其补角.设平面α与平面β的夹角为θ(),则
.
作业布置
作业: P38 练习 第3,4题
P43-44 习题1.4 第8,9,10,15题.
尽情享受学习数学的快乐吧!
我们下节课再见!
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
选择必修 第一章
1.4.2 用空间向量研究距离、夹角问题
第2课时 空间夹角
人教A版(2019)
教学目标
学习目标 数学素养
1.理解两异面直线所成角与它们的方向向量之间的关系,会用向量方法求两异面直线所成的角. 1.空间直观素养和运算素养.
2.理解直线与平面所成角与直线方向向量和平面法向量夹角之间的关系,会用向量方法求直线与平面所成的角. 2.空间直观素养和运算素养.
3.理解二面角的夹角与两个平面法向量的夹角之间的关系,会用向量方法求二面角的大小. 3.空间直观素养和运算素养.
温故知新
2.点到平面的距离
3.空间距离问题的转化
已知直线l的单位方向向量为,,设,则
.
已知平面α的法向量为,则
.
⑴求两条平行直线间的距离可转化为求其中一条直线上一点到另一条直线的距离.
⑵直线与平面平行,求它们之间的距离,可转化为求这条直线上一点到这个平面的距离.
⑶求两个平行平面间的距离,可转化为求其中一个平面上一点到另一个平面的距离.
1.点到直线的距离
新知探究
与距离类似,角度是立体几何中另一个重要的度量. 下面我们用向量方法研究直线与直线所成角、直线与平面所成角及平面与平面所成角.
【例1】如图,在棱长为1的正四面体(四个面都是正三角形)ABCD中,M,N分别为BC,AD的中点,求直线AM和CN夹角的余弦值.
分析:直线AM和CN夹角的余弦值,可以转化为求向量与夹角的余弦值,为此需要把向量用适当的极点表示出来,进而求得向量夹角的余弦值.
新知探究
解:
化为向量问题
如图,以{}作为基底,则
,
.
设向量与的夹角为θ,则直线AM和CN夹角的余弦值等于|cosθ|.
进行向量运算
.
.
.
又△ABC和△ACD均为等边三角形,
所以.
所以.
回到图形问题
所以直线AM和CN夹角的余弦值为.
新知探究
以上我们用向量方法解决了异面直线AM和CN所成角的问题,你能用向量方法求直线AB与平面BCD所成的角吗?
一般地,两条异面直线所成的角,可以转化为两条异面直线的方向向量的夹角来求得. 也就是说,若异面直线l1,l2所成的角为θ(),其方向向量分别是,则
.
新知探究
类似地,直线与平面所成的角,可以转化为直线的方向向量与平面的法向量的夹角.如图,直线AB与平面α相交于点B.设直线AB与平面α所成的角为θ,直线AB的方向向量为,平面α的法向量为,则
.
新知探究
如图,平面α与平面β相交,形成四个二面角,我们把这四个二面角中不大于90°的二面角称为平面α与平面β的夹角.
图中有几个二面角 两个平面的夹角与这两个平面形成的二面角有什么关系?
类似于两条异面直线所成的角.若平面α,β的法向量分别是和,则平面α与平面β的夹角即为向量和
的夹角或其补角.设平面α与平面β的夹角为θ(),则
.
新知探究
解:
以直线BA,BC,BB1分别为x轴,y轴,z轴,建立如图所示的空间直角坐标系.设AB=1,则
∴=(-,0,),=(0,1,1),
∴,
∴直线EF和BC1所成角的大小为.
【例2】如图,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AB=BC=AA1,∠ABC=90°,E,F分别是棱AB,BB1的中点,求直线EF和BC1所成角的大小.
B(0,0,0),E(,0,0),F(0,0,),C1(0,1,1).
新知探究
用向量法求异面直线所成角的一般步骤
⑴选好基底或建立空间直角坐标系;
⑵求出两直线的方向向量;
⑶代入公式求解.
新知探究
【例3】已知正三棱柱ABC-A1B1C1中的底面边长为a,侧棱长为a,M为A1B1的中点,求BC1与平面AMC1所成角的正弦值.
解:
如图,建立空间直角坐标系,则
A(0,0,0),B(0,,a,0),M(0,,),C1(,,),
∴(0,),=(,0,0,),=().
设BC1与平面AMC1所成角为θ,平面AMC1的法向量=(x,y,z),则
,
即,
取z=,则y=-4,x=0,=(0,-4,).
∴.
新知探究
用向量法求线面所成角的步骤
⑴建立恰当的空间直角坐标系.
⑵求直线的方向向量;
⑶求平面的法向量;
⑷计算:设线面角为θ,则.
新知探究
【例4】如图,在直三棱柱ABC-A1B1C1中,AC=CB=2,AA1=3,∠ACB=90°,P为BC的中点,点Q,R分别在棱AA1,BB1上,A1Q=2AQ,BR=2RB1.求平面PQR与平面A1B1C1夹角的余弦值.
解:
因为CC1⊥平面A1B1C1,所以平面A1B1C1的一个法向量
为=(0,0,1).
分析:因为平面PQR与平面A1B1C1夹角可以转化为平面PQR与平面A1B1C1的法向量的夹角,所以只需要求出这两个平面的法向量的夹角即可.
以C1为原点,以C1A1,C1B1,C1C所在直线为x轴,y轴,z轴,建立如图所示的空间直角坐标系.设平面A1B1C1的法向量为,平面PQR的法向量为,则平面PQR与平面A1B1C1的夹角就是与的夹角或其补角.
化为向量问题
进行向量运算
新知探究
【例4】如图,在直三棱柱ABC-A1B1C1中,AC=CB=2,AA1=3,∠ACB=90°,P为BC的中点,点Q,R分别在棱AA1,BB1上,A1Q=2AQ,BR=2RB1.求平面PQR与平面A1B1C1夹角的余弦值.
解:
设=(x,y,z),则
根据建立的空间直角坐标系,可知P(0,1,3),Q(2,0,2),R(0,2,1).
∴=(2,-1,-1),=(0,1,-2).
,
∴,
∴,
取=(3,4,2),则
新知探究
【例4】如图,在直三棱柱ABC-A1B1C1中,AC=CB=2,AA1=3,∠ACB=90°,P为BC的中点,点Q,R分别在棱AA1,BB1上,A1Q=2AQ,BR=2RB1.求平面PQR与平面A1B1C1夹角的余弦值.
解:
回到图形问题
取=(3,4,2),则
.
设平面PQR与平面A1B1C1的夹角为θ,则
.
即平面PQR与平面A1B1C1夹角的余弦值为.
新知探究
用向量法求平面与平面的夹角的步骤
⑴建立空间直角坐标系;
⑵求出两个平面的法向量;
⑶计算:设两个平面的夹角为θ,则.
初试身手
1.如图,在直三棱柱ABC-A1B1C1中,AC=3,BC=4,CC1=3,∠ACB=90°,则BC1与A1C所成的角的余弦值为( )
A. B. C. D.
如图,以C为坐标原点,CA,CB,CC1所在直线分别为x轴,y轴,z轴建立空间直角坐标系,则C(0,0,0),A1(3,0,3),B(0,4,0),C1(0,0,3),
∴(3,0,3),(0,-4,3),
解:
∴BC1与A1C所成的角的余弦值为.故选A.
∴.
A
初试身手
2.四棱锥P-ABCD中,底面为直角梯形,AD//BC,∠BAD=90°,PA⊥平面BACD,PA=AD=AB=2BC=2,M, N分别为PC, PB的中点.
⑴求证:PB⊥DM; ⑵求直线BD和平面ADMN所成角.
解:
如图,以A为原点,分别以AB,AD,AP所在直线为x轴、y轴、z轴建立空间直角坐标系Dxyz,则
A(0,0,0),B(2,0,0),D(0,2,0),P(0,0,2),N(1,01),M(1,,1).
⑵=(-2,2,0),=(0,2,0),=(1,0,1).
∴=0,
∴PB⊥DM.
x
y
z
⑴=(2,0,-2),=(1,,1),
初试身手
2.四棱锥P-ABCD中,底面为直角梯形,AD//BC,∠BAD=90°,PA⊥平面BACD,PA=AD=AB=2BC=2,M, N分别为PC, PB的中点.
⑴求证:PB⊥DM; ⑵求直线BD和平面ADMN所成角.
解:
设平面ADMN的一个法向量=(x,y,z),则
, 即.
⑵=(-2,2,0),=(0,2,0),=(1,0,1).
∴=(1,0,-1),
.
x
y
z
取x=1,则z=-1,
设直线BD和平面ADMN所成角为θ,则
∴θ.
即直线BD和平面ADMN所成角为.
初试身手
解:
⑴在三棱锥P-ABC中,PA⊥底面ABC,∠BAC=90°,故以A为坐标原点,AB,AC,AP所在的直线分别为x轴,y轴,z轴,建立如图所示的空间直角坐标系.
因为D,E,N分别为棱PA,PC,BC的中点,M是线段AD上靠近点A的三等分点,PA=6,AC=4,AB=2,所以M(0,0,1),B(2,0,0),C(0,4,0),N(1,2,0),D(0,0,3),P(0,0,6),E(0,2,3),
∴=(-1,-2,3),=(-2,2,3),
3.如图,在三棱锥P-ABC中,PA⊥底面ABC,∠BAC=90°.D,E,N分别为棱PA,PC,BC的中点,M是线段AD上靠近点A的三等分点,PA=6,AC=4,AB=2.求:
⑴直线ND与直线BE所成角的余弦值;
⑵平面CEM与平面MNE夹角的余弦值.
初试身手
解:
设直线ND与直线BE所成角为θ,则
,
即直线ND与直线BE所成角的余弦值为.
3.如图,在三棱锥P-ABC中,PA⊥底面ABC,∠BAC=90°.D,E,N分别为棱PA,PC,BC的中点,M是线段AD上靠近点A的三等分点,PA=6,AC=4,AB=2.求:
⑴直线ND与直线BE所成角的余弦值;
⑵平面CEM与平面MNE夹角的余弦值.
⑵由⑴得=(1,2,-1),=(0,4,-1),=(0,2,2).
设平面MNE的法向量为=(a,b,c),则
,即,解得,
取c=1,则a=3,b=-1,得=(3,-1,1),
初试身手
解:
易知AB⊥平面CEM,故可设平面CEM的一个法向量为=(1,0,0).
,
设平面CEM与平面MNE的夹角为α,
3.如图,在三棱锥P-ABC中,PA⊥底面ABC,∠BAC=90°.D,E,N分别为棱PA,PC,BC的中点,M是线段AD上靠近点A的三等分点,PA=6,AC=4,AB=2.求:
⑴直线ND与直线BE所成角的余弦值;
⑵平面CEM与平面MNE夹角的余弦值.
即平面CEM与平面MNE夹角的余弦值为
课堂小结
1.用向量法求异面直线所成角
2.用向量法求线面所成角
3.用向量法求平面与平面的夹角
若异面直线l1,l2所成的角为θ(),其方向向量分别是,则
设直线AB与平面α所成的角为θ,直线AB的方向向量为,平面α的法向量为,则
.
.
若平面α,β的法向量分别是和,则平面α与平面β的夹角即为向量和的夹角或其补角.设平面α与平面β的夹角为θ(),则
.
作业布置
作业: P38 练习 第3,4题
P43-44 习题1.4 第8,9,10,15题.
尽情享受学习数学的快乐吧!
我们下节课再见!
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
