福建省闽清县天儒中学(人教版)数学九年级上册课件:22-1-1 二次函数(共27张PPT)
文档属性
| 名称 | 福建省闽清县天儒中学(人教版)数学九年级上册课件:22-1-1 二次函数(共27张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 733.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-01-01 00:00:00 | ||
图片预览







文档简介
课件27张PPT。22.1.1 二次函数学科网基础回顾 什么叫函数? 在某变化过程中的两个变量x、y,当变量x在某个范围内取一个确定的值,另一个变量y总有唯一的值与它对应。
这样的两个变量之间的关系我们把它叫做函数关系。
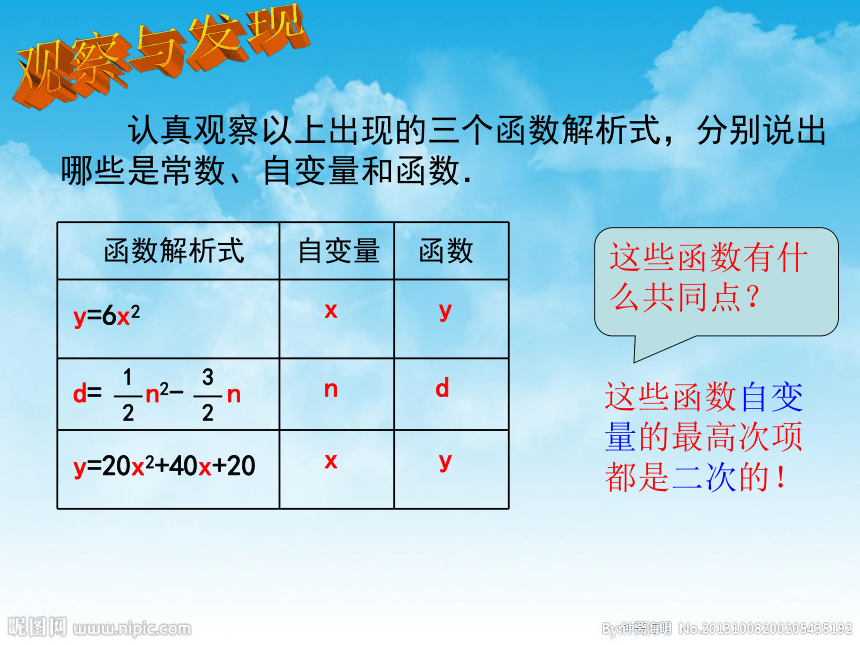
对于上述变量x 、y,我们把y叫x的函数。 x叫自变量, y叫变量。目前,我们已经学习了那几种类型的函数?二次函数变量之间的关系函数函数知多少讨论与思考:1、正方形的六个面是全等的正方形,设正方体的棱长为x,表面积为y,显然对于x的每一个值,y都有一个对应值,即y是x的函数,他们的具体关系是可以表示为什么?2、多边形的对角线数d与边数n有什么关系?3、某工厂一种产品现在的年产量是20件,计划今后两年增加产量。如果每年都比上一年的产量增加x倍,那么两年后这种产品的产量y将随计划所定的x的值而确定,y与x之间的关系应怎样表示?y=6x2即y=20(1+x)2即y=20x2+40x+20xyydxxn观察与发现 认真观察以上出现的三个函数解析式,分别说出哪些是常数、自变量和函数.这些函数有什么共同点?这些函数自变量的最高次项都是二次的!定义:一般地,形如y=ax2+bx+c(a,b,c是常数,a≠ 0)的函数叫做x的二次函数。(1)等号左边是变量y,右边是关于自变量x的(3 )等式的右边最高次数为 ,可以没有一次项和常数项,但不能没有二次项。注意:(2)a,b,c为常数,且整式a≠0.2二次函数的一般形式:y=ax2+bx+c (其中a、b、c是常数,a≠0)
二次函数的特殊形式:
当b=0时, y=ax2+c
当c=0时, y=ax2+bx
当b=0,c=0时, y=ax2一次函数正比例函数二次函数这些函数的名称度反映了函数表达式与自变量的关系。二次函数的定义: 注意:1、其中,x是自变量,ax2是二次项,a是二次项系数
bx是一次项,b是一次项系数
c是常数项。归纳与总结2、函数的右边最高次数为2,可以没有一次项和常数项,
但不能没有二次项.也就是a不能等于0
知识运用
例1:下列函数中,哪些是二次函数?
(1)y=3x-1 ( ) (2)y=3x2 ( )
(3)y=3x3+2x2 ( ) (4)y=2x2-2x+1( )
(5)y=x-2+x ( ) (6)y=x2-x(1+x) ( )不是是不是不是是不是先化简后判断 1、 说出下列二次函数的二次项系数、一次项系
数、常数项(1) y=-x2+58x-112
(2)y=πx22、指出下列函数y=ax2+bx+c中的a、b、c(1) y=-3x2-x-1(3) y=x(1+x)(2) y=5x2-6
看谁反应快例题讲解例下列函数中,哪些是二次函数?若是,分别指出二次项系数,一次项系数,常数项。
(1) y=3(x-1)2+1 (2) y=x+
(3) s=3-2t2 (4) y=(x+3)2-x2
(5)y= -x (6) v=8π r2
解:y=3(x-1)2+1
=3(x2-2x+1)+1
=3x2-6x+3+1
即y=3x2-6x+4是二次函数.二次项系数:一次项系数:常数项:3-64不是二次函数.(3) s=3-2t2是二次函数.二次项系数:一次项系数:常数项:-203(4) y=(x+3)2-x2=x2+6x+9-x2
即y=6x+9不是二次函数. 二次项系数: 一次项系数: 常数项:8π00 不是二次函数. (6) v=8π r2 是二次函数.驶向胜利的彼岸知识运用m2—2m-1=2 m+1 ≠0 ∴m=3例2:m取何值时, 函数y= (m+1)x
+(m-3)x+m 是二次函数? 解:由题意得注意:二次函数的二次项系数不能为零
练习1: 关于x的函数 是二次函数, 求m的值.解: 由题意可得注意:二次函数的二次项系数不能为零练习2若函数 为二次函数,求m的值。解:因为该函数为二次函数,
则解(1)得:m=2或-1解(2)得:所以m=24.函数 y=(m-n)x2+ mx+n 是二次函数的条件是( )
A m,n是常数,且m≠0 B m,n是常数,且n≠0
C m,n是常数,且m≠n D m,n为任何实数B C想一想例题讲解解:(1)当m2-7=1且m+3≠0即m=± 时是正比例函数。(2)当m2-7=-1且m+3≠0即m=± 时是反比例函数。(3)当m2-7=2且m+3≠0即m=3时是二次函数。例4:已知关于x的二次函数,当x=-1时,函数值为10,当x=1时,函数值为4,当x=2时,函数值为7,求这个二次函数的解析试.{待定系数法4. 已知二次函数y=x2+px+q,当x=1时,函数值为4,当x=2时,函数值为- 5, 求这个二次函数的解析式.{ 圆的半径是1cm,假设半径增加xcm时,圆的面积增加ycm2.
(1)写出y与x之间的函数关系表达式;
(2)当圆的半径分别增加1cm, ,2cm时,圆的面积增加多少?
试一试:
要用长20m的铁栏杆,一面靠墙,围成一个矩形的花圃,设连墙的一边为x,矩形的面积为y,试(1)写出y关与x的函数关系式.
(2)当x=3时,矩形的面积为多少?(o(1)写出正方体的表面积S(cm2)与正方体棱长a(cm)之间的函数关系;
(2)写出圆的面积y(cm2)与它的周长x(cm)之间的函数关系;
(3)菱形的两条对角线的和为26cm,求菱形的面积S(cm2)与一对角线长x(cm)之间的函数关系.(2)由题意得 其中y是x的二次函数;(3)由题意得 其中S是x的
二次函数解: (1)由题意得 其中S是a的二次函数;在种树问题中,种多少棵橙子树,可以使果园橙子的总产量最多? 6037560420604556048060495605006049560480604556042060375问题再探究y=-5x2+100x+60000,你能根据表格中的数据作出猜测吗?你发现了吗?回味无穷定义中应该注意的几个问题: 1.定义:一般地,形如y=ax2+bx+c(a,b,c是常数,a≠0)的函数叫做x的二次函数.
y=ax2+bx+c(a,b,c是常数,a≠0)的几种不同表示形式:
(1)y=ax2(a≠0,b=0,c=0,).
(2)y=ax2+c(a≠0,b=0,c≠0).
(3)y=ax2+bx(a≠0,b≠0,c=0).
2.定义的实质是:ax2+bx+c是整式,自变量x的最高次数是二次,自变量x的取值范围是全体实数.
这样的两个变量之间的关系我们把它叫做函数关系。
对于上述变量x 、y,我们把y叫x的函数。 x叫自变量, y叫变量。目前,我们已经学习了那几种类型的函数?二次函数变量之间的关系函数函数知多少讨论与思考:1、正方形的六个面是全等的正方形,设正方体的棱长为x,表面积为y,显然对于x的每一个值,y都有一个对应值,即y是x的函数,他们的具体关系是可以表示为什么?2、多边形的对角线数d与边数n有什么关系?3、某工厂一种产品现在的年产量是20件,计划今后两年增加产量。如果每年都比上一年的产量增加x倍,那么两年后这种产品的产量y将随计划所定的x的值而确定,y与x之间的关系应怎样表示?y=6x2即y=20(1+x)2即y=20x2+40x+20xyydxxn观察与发现 认真观察以上出现的三个函数解析式,分别说出哪些是常数、自变量和函数.这些函数有什么共同点?这些函数自变量的最高次项都是二次的!定义:一般地,形如y=ax2+bx+c(a,b,c是常数,a≠ 0)的函数叫做x的二次函数。(1)等号左边是变量y,右边是关于自变量x的(3 )等式的右边最高次数为 ,可以没有一次项和常数项,但不能没有二次项。注意:(2)a,b,c为常数,且整式a≠0.2二次函数的一般形式:y=ax2+bx+c (其中a、b、c是常数,a≠0)
二次函数的特殊形式:
当b=0时, y=ax2+c
当c=0时, y=ax2+bx
当b=0,c=0时, y=ax2一次函数正比例函数二次函数这些函数的名称度反映了函数表达式与自变量的关系。二次函数的定义: 注意:1、其中,x是自变量,ax2是二次项,a是二次项系数
bx是一次项,b是一次项系数
c是常数项。归纳与总结2、函数的右边最高次数为2,可以没有一次项和常数项,
但不能没有二次项.也就是a不能等于0
知识运用
例1:下列函数中,哪些是二次函数?
(1)y=3x-1 ( ) (2)y=3x2 ( )
(3)y=3x3+2x2 ( ) (4)y=2x2-2x+1( )
(5)y=x-2+x ( ) (6)y=x2-x(1+x) ( )不是是不是不是是不是先化简后判断 1、 说出下列二次函数的二次项系数、一次项系
数、常数项(1) y=-x2+58x-112
(2)y=πx22、指出下列函数y=ax2+bx+c中的a、b、c(1) y=-3x2-x-1(3) y=x(1+x)(2) y=5x2-6
看谁反应快例题讲解例下列函数中,哪些是二次函数?若是,分别指出二次项系数,一次项系数,常数项。
(1) y=3(x-1)2+1 (2) y=x+
(3) s=3-2t2 (4) y=(x+3)2-x2
(5)y= -x (6) v=8π r2
解:y=3(x-1)2+1
=3(x2-2x+1)+1
=3x2-6x+3+1
即y=3x2-6x+4是二次函数.二次项系数:一次项系数:常数项:3-64不是二次函数.(3) s=3-2t2是二次函数.二次项系数:一次项系数:常数项:-203(4) y=(x+3)2-x2=x2+6x+9-x2
即y=6x+9不是二次函数. 二次项系数: 一次项系数: 常数项:8π00 不是二次函数. (6) v=8π r2 是二次函数.驶向胜利的彼岸知识运用m2—2m-1=2 m+1 ≠0 ∴m=3例2:m取何值时, 函数y= (m+1)x
+(m-3)x+m 是二次函数? 解:由题意得注意:二次函数的二次项系数不能为零
练习1: 关于x的函数 是二次函数, 求m的值.解: 由题意可得注意:二次函数的二次项系数不能为零练习2若函数 为二次函数,求m的值。解:因为该函数为二次函数,
则解(1)得:m=2或-1解(2)得:所以m=24.函数 y=(m-n)x2+ mx+n 是二次函数的条件是( )
A m,n是常数,且m≠0 B m,n是常数,且n≠0
C m,n是常数,且m≠n D m,n为任何实数B C想一想例题讲解解:(1)当m2-7=1且m+3≠0即m=± 时是正比例函数。(2)当m2-7=-1且m+3≠0即m=± 时是反比例函数。(3)当m2-7=2且m+3≠0即m=3时是二次函数。例4:已知关于x的二次函数,当x=-1时,函数值为10,当x=1时,函数值为4,当x=2时,函数值为7,求这个二次函数的解析试.{待定系数法4. 已知二次函数y=x2+px+q,当x=1时,函数值为4,当x=2时,函数值为- 5, 求这个二次函数的解析式.{ 圆的半径是1cm,假设半径增加xcm时,圆的面积增加ycm2.
(1)写出y与x之间的函数关系表达式;
(2)当圆的半径分别增加1cm, ,2cm时,圆的面积增加多少?
试一试:
要用长20m的铁栏杆,一面靠墙,围成一个矩形的花圃,设连墙的一边为x,矩形的面积为y,试(1)写出y关与x的函数关系式.
(2)当x=3时,矩形的面积为多少?(o
(2)写出圆的面积y(cm2)与它的周长x(cm)之间的函数关系;
(3)菱形的两条对角线的和为26cm,求菱形的面积S(cm2)与一对角线长x(cm)之间的函数关系.(2)由题意得 其中y是x的二次函数;(3)由题意得 其中S是x的
二次函数解: (1)由题意得 其中S是a的二次函数;在种树问题中,种多少棵橙子树,可以使果园橙子的总产量最多? 6037560420604556048060495605006049560480604556042060375问题再探究y=-5x2+100x+60000,你能根据表格中的数据作出猜测吗?你发现了吗?回味无穷定义中应该注意的几个问题: 1.定义:一般地,形如y=ax2+bx+c(a,b,c是常数,a≠0)的函数叫做x的二次函数.
y=ax2+bx+c(a,b,c是常数,a≠0)的几种不同表示形式:
(1)y=ax2(a≠0,b=0,c=0,).
(2)y=ax2+c(a≠0,b=0,c≠0).
(3)y=ax2+bx(a≠0,b≠0,c=0).
2.定义的实质是:ax2+bx+c是整式,自变量x的最高次数是二次,自变量x的取值范围是全体实数.
同课章节目录
