2023-2024学年内蒙古自治区巴彦淖尔市高一下学期7月期末考试数学试题(含答案)
文档属性
| 名称 | 2023-2024学年内蒙古自治区巴彦淖尔市高一下学期7月期末考试数学试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 330.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-26 19:16:20 | ||
图片预览



文档简介
2023-2024学年内蒙古自治区巴彦淖尔市高一下学期7月期末考试
数学试题
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.在复平面内对应的点位于( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
2.在正中,向量在方向上的投影向量为( )
A. B. C. D.
3.在中,角的对边分别是,若,则( )
A. 或 B. 或 C. D.
4.某商场评选金牌销售员,现将该商场所有销售员某月的销售额进行整理,得到如图所示的统计图,则该商场这个月所有销售员销售额的平均数为( )
A. 万元 B. 万元 C. 万元 D. 万元
5.已知是三个不同的平面,是两条不同的直线,则下列命题是真命题的是( )
A. 若,则
B. 若,则
C. 若,则
D. 若,则
6.某公司对员工的工作绩效进行评估,得到一组数据,后来复查数据时,又将重复记录在数据中,则这组新的数据和原来的数据相比,一定不会改变的是( )
A. 平均数 B. 中位数 C. 极差 D. 众数
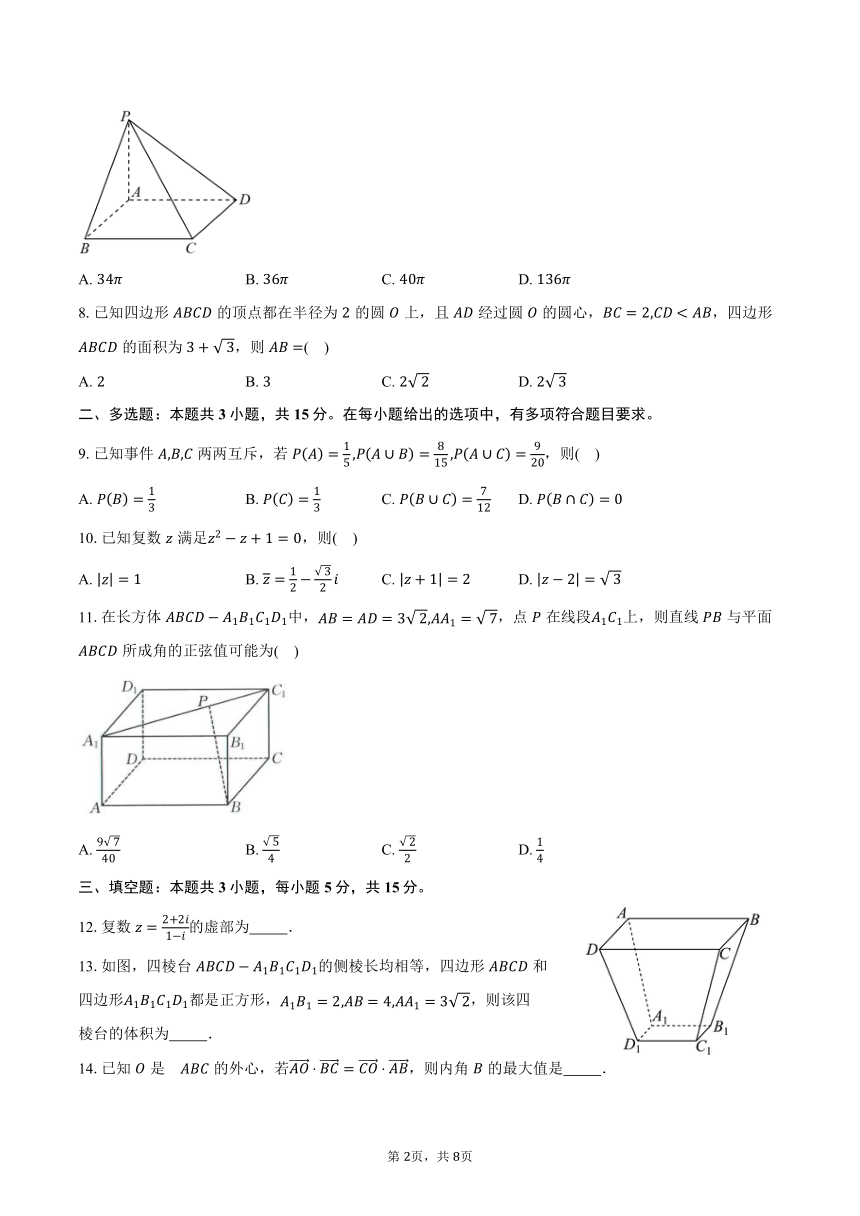
7.如图,在四棱锥中,底面是矩形,平面,则该四棱锥外接球的表面积为( )
A. B. C. D.
8.已知四边形的顶点都在半径为的圆上,且经过圆的圆心,,四边形的面积为,则( )
A. B. C. D.
二、多选题:本题共3小题,共15分。在每小题给出的选项中,有多项符合题目要求。
9.已知事件两两互斥,若,则( )
A. B. C. D.
10.已知复数满足,则( )
A. B. C. D.
11.在长方体中,,点在线段上,则直线与平面所成角的正弦值可能为( )
A. B. C. D.
三、填空题:本题共3小题,每小题5分,共15分。
12.复数的虚部为 .
13.如图,四棱台的侧棱长均相等,四边形和
四边形都是正方形,,则该四
棱台的体积为 .
14.已知是的外心,若,则内角的最大值是 .
四、解答题:本题共5小题,共60分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
已知向量,.
若,求;
若向量,,求与夹角的余弦值.
16.本小题分
某工厂计划对该工厂生产的某类产品进行深加工,以推进该类产品的升级.该工厂随机抽取某生产线上一段时间内生产的件产品,对其质量单位:进行统计,并将样本数据分为六组,得到如下频率分布直方图.
试估计样本数据的分位数;
从样本数据在内的产品中采用分层随机抽样的方法抽取件产品作为产品深加工方案制定的分析样例,再从被抽取的这件产品中随机抽取件产品作为深加工的标准样例,求标准样例中恰有件产品的质量在内的概率;
若规定质量在内的产品为优等品,用频率估计概率,从该生产线上随机抽取件产品,求抽取到的产品中至少有件优等品的概率.
17.本小题分
某校举办环保知识竞赛,初赛中每位参赛者有三次答题机会,每次回答一道题,若答对,则通过初赛,否则直到三次机会用完已知甲乙丙都参加了这次环保知识竞赛,且他们每次答对题目的概率都是,假设甲乙丙每次答题是相互独立的,且甲乙丙的答题结果也是相互独立的.
求甲第二次答题通过初赛的概率;
求乙通过初赛的概率;
求甲、乙、丙三人中恰有两人通过初赛的概率.
18.本小题分
是直线外一点,点在直线上点与两点均不重合,我们称如下操作为“由点对施以视角运算”:若点在线段上,记;若点在线段外,记在中,角的对边分别是,点在射线上.
若是角的平分线,且,由点对施以视角运算,求的值;
若,由点对施以视角运算,,求的周长.
19.本小题分
在四棱锥中,平面,平面平面分别为的中点.
证明:平面.
证明:.
若二面角的正切值为,求三棱锥的体积.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14. 或
15.解:因为,,所以.
由,可得,
即,解得,
所以,故.
依题意得.
因为,所以
解得,则.
,,,
所以,
所以与夹角的余弦值为.
16.解:由频率分布直方图知,样本数据在的频率为,在的频率为,
则样本数据的分位数,于是,解得,
所以样本数据的分位数约为.
样本数据在内的产品被抽取的件数为,记为,
样本数据在内的产品被抽取的件数为,记为
则从被抽取的这件产品中随机抽取件产品的情况有:
,共种,
其中标准样例中恰有件产品的质量在内的情况有种.
所以标准样例中恰有件产品的质量在内的概率为.
依题意,从该生产线上随机抽取件产品,该件产品为优等品的概率为,
则抽取到的产品中至少有件优等品的概率为.
17.解:记甲第二次答题通过初赛为事件,则;
记乙通过初赛为事件,则;
依题意甲、乙、丙每人通过初赛的概率均为,
记甲、乙、丙三人中恰有两人通过初赛为事件,
则.
18.解:因为是角的平分线,所以且在线段上,
所以,
又,所以;
因为点在射线上,,且,所以在线段外,且,
所以,
所以,
在中,由余弦定理可得,
即,解得负值已舍去,
所以,
所以的周长为.
19.解:如图,连接.
因为分别为的中点,所以为的中位线,则.
因为平面平面,所以平面 如图,过作交于.
因平面平面,平面平面,平面,故平面.
因为平面,所以.
因为平面平面,所以.
因为,所以平面,
又平面,所以.
如图,过作交于,过作交于,连接.
因平面,平面,则,
因平面,故得平面.
因平面,则.
因为,平面,所以平面.
又平面,则,则即为二面角的平面角,
依题意,.
设,则因为,所以.
由,得,即,则.
又由,得,即,解得.
因,则的面积为,
故
第1页,共1页
数学试题
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.在复平面内对应的点位于( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
2.在正中,向量在方向上的投影向量为( )
A. B. C. D.
3.在中,角的对边分别是,若,则( )
A. 或 B. 或 C. D.
4.某商场评选金牌销售员,现将该商场所有销售员某月的销售额进行整理,得到如图所示的统计图,则该商场这个月所有销售员销售额的平均数为( )
A. 万元 B. 万元 C. 万元 D. 万元
5.已知是三个不同的平面,是两条不同的直线,则下列命题是真命题的是( )
A. 若,则
B. 若,则
C. 若,则
D. 若,则
6.某公司对员工的工作绩效进行评估,得到一组数据,后来复查数据时,又将重复记录在数据中,则这组新的数据和原来的数据相比,一定不会改变的是( )
A. 平均数 B. 中位数 C. 极差 D. 众数
7.如图,在四棱锥中,底面是矩形,平面,则该四棱锥外接球的表面积为( )
A. B. C. D.
8.已知四边形的顶点都在半径为的圆上,且经过圆的圆心,,四边形的面积为,则( )
A. B. C. D.
二、多选题:本题共3小题,共15分。在每小题给出的选项中,有多项符合题目要求。
9.已知事件两两互斥,若,则( )
A. B. C. D.
10.已知复数满足,则( )
A. B. C. D.
11.在长方体中,,点在线段上,则直线与平面所成角的正弦值可能为( )
A. B. C. D.
三、填空题:本题共3小题,每小题5分,共15分。
12.复数的虚部为 .
13.如图,四棱台的侧棱长均相等,四边形和
四边形都是正方形,,则该四
棱台的体积为 .
14.已知是的外心,若,则内角的最大值是 .
四、解答题:本题共5小题,共60分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
已知向量,.
若,求;
若向量,,求与夹角的余弦值.
16.本小题分
某工厂计划对该工厂生产的某类产品进行深加工,以推进该类产品的升级.该工厂随机抽取某生产线上一段时间内生产的件产品,对其质量单位:进行统计,并将样本数据分为六组,得到如下频率分布直方图.
试估计样本数据的分位数;
从样本数据在内的产品中采用分层随机抽样的方法抽取件产品作为产品深加工方案制定的分析样例,再从被抽取的这件产品中随机抽取件产品作为深加工的标准样例,求标准样例中恰有件产品的质量在内的概率;
若规定质量在内的产品为优等品,用频率估计概率,从该生产线上随机抽取件产品,求抽取到的产品中至少有件优等品的概率.
17.本小题分
某校举办环保知识竞赛,初赛中每位参赛者有三次答题机会,每次回答一道题,若答对,则通过初赛,否则直到三次机会用完已知甲乙丙都参加了这次环保知识竞赛,且他们每次答对题目的概率都是,假设甲乙丙每次答题是相互独立的,且甲乙丙的答题结果也是相互独立的.
求甲第二次答题通过初赛的概率;
求乙通过初赛的概率;
求甲、乙、丙三人中恰有两人通过初赛的概率.
18.本小题分
是直线外一点,点在直线上点与两点均不重合,我们称如下操作为“由点对施以视角运算”:若点在线段上,记;若点在线段外,记在中,角的对边分别是,点在射线上.
若是角的平分线,且,由点对施以视角运算,求的值;
若,由点对施以视角运算,,求的周长.
19.本小题分
在四棱锥中,平面,平面平面分别为的中点.
证明:平面.
证明:.
若二面角的正切值为,求三棱锥的体积.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14. 或
15.解:因为,,所以.
由,可得,
即,解得,
所以,故.
依题意得.
因为,所以
解得,则.
,,,
所以,
所以与夹角的余弦值为.
16.解:由频率分布直方图知,样本数据在的频率为,在的频率为,
则样本数据的分位数,于是,解得,
所以样本数据的分位数约为.
样本数据在内的产品被抽取的件数为,记为,
样本数据在内的产品被抽取的件数为,记为
则从被抽取的这件产品中随机抽取件产品的情况有:
,共种,
其中标准样例中恰有件产品的质量在内的情况有种.
所以标准样例中恰有件产品的质量在内的概率为.
依题意,从该生产线上随机抽取件产品,该件产品为优等品的概率为,
则抽取到的产品中至少有件优等品的概率为.
17.解:记甲第二次答题通过初赛为事件,则;
记乙通过初赛为事件,则;
依题意甲、乙、丙每人通过初赛的概率均为,
记甲、乙、丙三人中恰有两人通过初赛为事件,
则.
18.解:因为是角的平分线,所以且在线段上,
所以,
又,所以;
因为点在射线上,,且,所以在线段外,且,
所以,
所以,
在中,由余弦定理可得,
即,解得负值已舍去,
所以,
所以的周长为.
19.解:如图,连接.
因为分别为的中点,所以为的中位线,则.
因为平面平面,所以平面 如图,过作交于.
因平面平面,平面平面,平面,故平面.
因为平面,所以.
因为平面平面,所以.
因为,所以平面,
又平面,所以.
如图,过作交于,过作交于,连接.
因平面,平面,则,
因平面,故得平面.
因平面,则.
因为,平面,所以平面.
又平面,则,则即为二面角的平面角,
依题意,.
设,则因为,所以.
由,得,即,则.
又由,得,即,解得.
因,则的面积为,
故
第1页,共1页
同课章节目录
