2023-2024学年宁夏回族自治区银川一中高一下学期期末考试数学试卷(含答案)
文档属性
| 名称 | 2023-2024学年宁夏回族自治区银川一中高一下学期期末考试数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 396.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-26 20:55:51 | ||
图片预览



文档简介
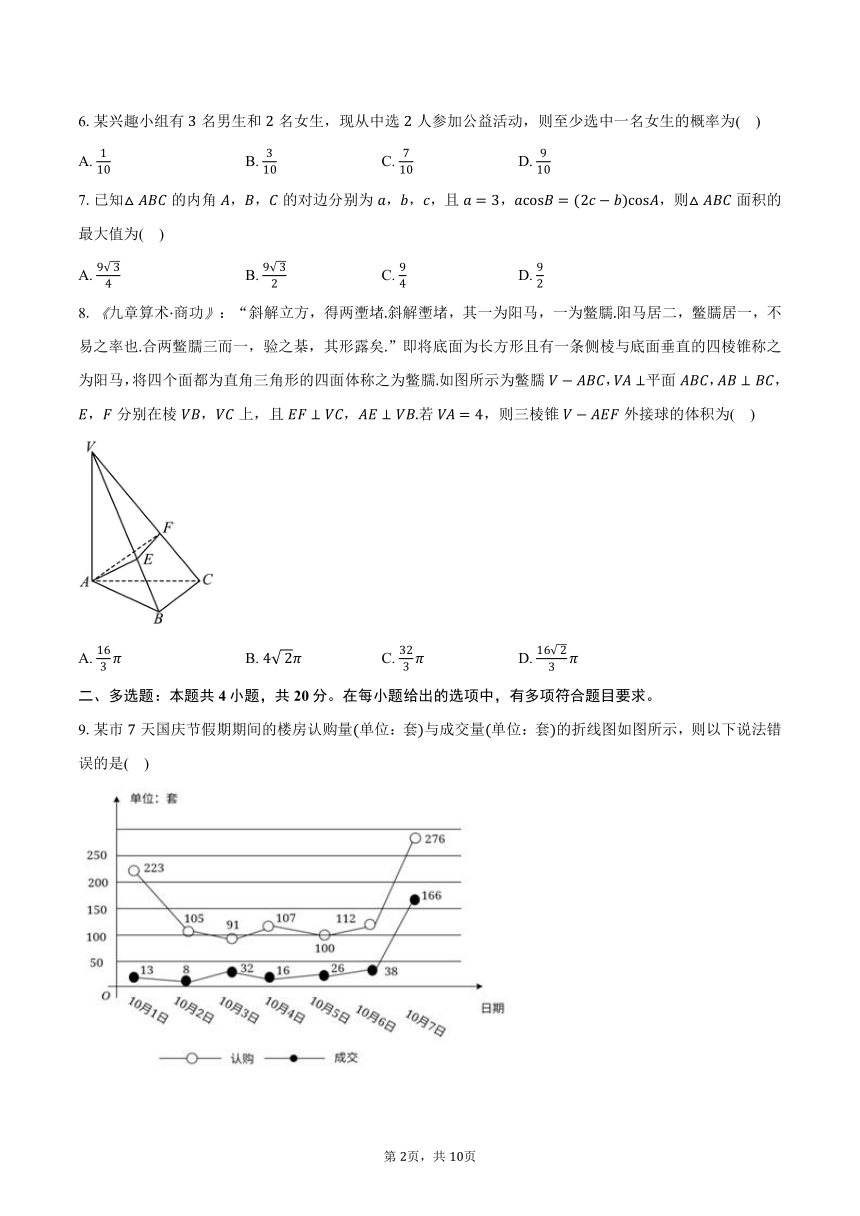
2023-2024学年宁夏回族自治区银川一中高一下学期期末考试
数学试卷
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.若,,,则的值为( )
A. B. C. D.
2.已知是三个不同的平面,是两条不同的直线,则下列命题正确的是( )
A. 若,,则 B. 若,,则
C. 若,,则 D. 若,,则
3.如图,样本和分别取自两个不同的总体,它们的样本平均数分别为和,样本标准差分别为和,则( )
A. , B. ,
C. , D. ,
4.已知为随机事件,与互斥,与互为对立,且,则( )
A. B. C. D.
5.如图,在直三棱柱中,,点为的中点,则异面直线与所成的角为( )
A. B. C. D.
6.某兴趣小组有名男生和名女生,现从中选人参加公益活动,则至少选中一名女生的概率为( )
A. B. C. D.
7.已知的内角,,的对边分别为,,,且,,则面积的最大值为( )
A. B. C. D.
8.九章算术商功:“斜解立方,得两壍堵斜解壍堵,其一为阳马,一为鳖臑阳马居二,鳖臑居一,不易之率也合两鳖臑三而一,验之棊,其形露矣”即将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑如图所示为鳖臑,平面,,,分别在棱,上,且,若,则三棱锥外接球的体积为( )
A. B. C. D.
二、多选题:本题共4小题,共20分。在每小题给出的选项中,有多项符合题目要求。
9.某市天国庆节假期期间的楼房认购量单位:套与成交量单位:套的折线图如图所示,则以下说法错误的是( )
A. 成交量的中位数是 B. 日成交量超过日平均成交量的有天
C. 认购量越大,则成交量就越大 D. 认购量的第一四分位数是
10.已知事件,相互独立,且,,则( )
A. B.
C. D.
11.已知圆台的上、下底面半径分别为和,母线长为,则( )
A. 圆台的高为 B. 圆台的侧面积为
C. 圆台的体积为 D. 圆台的轴截面面积为
12.如图,正方体的棱长为,是侧面上的一个动点含边界,点在棱上,且,则下列结论正确的有( )
A. 平面被正方体截得截面为三角形
B. 若,直线
C. 若在上,的最小值为
D. 若,点 的轨迹长度为
三、填空题:本题共4小题,每小题5分,共20分。
13.某眼科医院为了了解高中学生的视力情况,利用分层抽样的方法从某高中三个年级中抽取了人进行问卷调查,其中高一年级抽取了人,高二年级抽取了人,且高三年级共有学生人,则该高中三个年级的学生总数为 人.
14.在正方体中,为的中点,则与平面所成角的正弦值为 .
15.甲、乙两支羽毛球队体检结果如下:甲队的体重的平均数为,方差为,乙队体重的平均数为,方差为,又已知甲、乙两队的队员人数之比为,那么甲、乙两队全部队员的方差等于 .
16.电路从到上共连接着个灯泡如图,每个灯泡断路的概率是,整个电路的连通与否取决于灯泡是否断路.则从到连通的概率是 .
四、解答题:本题共6小题,共72分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
在中,角,,的对边分别为,,,且,.
若,求的值;
若的面积为,求的值.
18.本小题分
如图所示,三棱柱,是的中点,是的中点.求证:
平面;
平面平面D.
19.本小题分
新高考实行“”选科模式,其中“”为必考科目,语文、数学、外语所有学生必考;“”为首选科目,从物理、历史中选择一科;“”为再选科目,从化学、生物学、地理、思想政治中任选两科某大学的某专业要求首选科目为物理,再选科目中化学、生物学至少选一科.
写出所有选科组合的样本空间从所有选科组合中随机选一种组合,并且每种组合被选到的可能性相等,求所选组合符合该大学某专业报考条件的概率;
甲、乙两位同学独立进行选科,求两人中至少有一人符合该大学某专业报考条件的概率.
20.本小题分
如图,四棱锥中,平面,四边形为梯形,,,,是上一点且,.
Ⅰ求证:平面;
Ⅱ求点到平面的距离.
21.本小题分
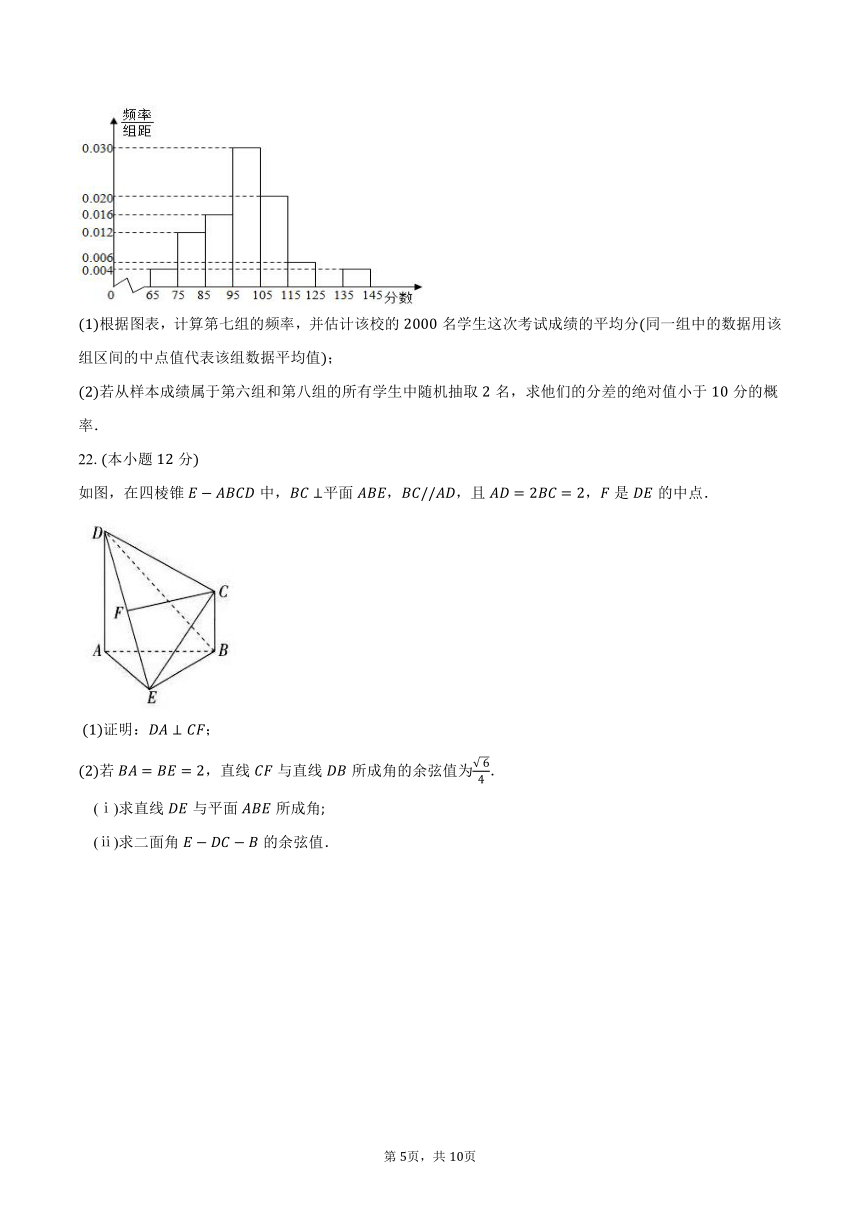
某校在一次期末数学测试中,为统计学生的考试情况,从学校的名学生中随机抽取名学生的考试成绩,被测学生成绩全部介于分到分之间满分分,将统计结果按如下方式分成八组:第一组,第二组,第八组,如图是按上述分组方法得到的频率分布直方图的一部分.
根据图表,计算第七组的频率,并估计该校的名学生这次考试成绩的平均分同一组中的数据用该组区间的中点值代表该组数据平均值;
若从样本成绩属于第六组和第八组的所有学生中随机抽取名,求他们的分差的绝对值小于分的概率.
22.本小题分
如图,在四棱锥中,平面,,且,是的中点.
证明:;
若,直线与直线所成角的余弦值为.
(ⅰ)求直线与平面所成角
(ⅱ)求二面角的余弦值.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14. 或
15.
16.
17.解:在中,,
,即.
,
则,
解得,
又,
,
.
18.证明:由题意,是三棱柱,
连接,与交于,连接,可得,
平面,平面,
平面D.
是的中点,是的中点,
,四边形为平行四边形,
,
又平面,平面,
平面,
由可知平面,
又,B、平面,
平面平面D.
19.解:依题意,样本空间为物化生,物化地,物化政,物生地,物生政,物地政,史化生,史化地,史化政,史生地,史生政,史地政,,
记事件“所选组合符合该大学某专业报考条件”,则物化生,物化地,物化政,物生地,物生政,,所以.
记事件“甲符合该大学某专业报考条件”,
事件“乙符合该大学某专业报考条件”,
事件“甲、乙两人中至少有一人符合该大学某专业报考条件”,
由可知,,
所以.
20.Ⅰ证明:平面,平面,
,
又,,、平面,
平面,又平面,
.
又平面,平面,
,
又,、平面,
平面,
Ⅱ解:由,且为梯形,,且,
则为菱形,所以,
由得,,又,所以,
则
从而有是边长为的等边三角形.
在中:,,
设到平面的距离为,
由得,
,
解得,
即到平面的距离为.
21.解:由频率分布直方图得第七组的频率为:
.
用样本数据估计该校的名学生这次考试成绩的平均分为:
.
样本成绩属于第六组的有人,设为,
样本成绩属于第八组的有人,设为,
从样本成绩属于第六组和第八组的所有学生中随机抽取名,
基本事件有:,,,,,,,,,共个
他们的分差的绝对值小于分,即在同一组中包含的基本事件有:,,,共个
他们的分差的绝对值小于分的概率.
22.解:取的中点,连接,,如图所示,
因为平面,平面,所以,
因为,所以,
平面,,所以平面,
因为平面,所以,
在中,因为,分别为,的中点,则,,
又,,所以,,所以四边形为平行四边形,
所以,
因为,所以.
连接,如图,
在中,,,所以,
因为,平面,平面,,所以平面,
因为平面,所以,
因为,所以与所成角与与所成角相等,
在中,,,所以,
所以,
由知平面,所以直线与平面所成角为,
在中,,所以,
所以直线与平面所成角为.
延长,交的延长线于,连结,如图所示,
取的中点,在中,过点作的垂线,垂足为,连接,
因为,,所以,
因为平面,平面,所以,
因为平面,平面,,所以平面,
因为平面,所以,
因为,平面,平面,,所以平面,
因为平面,所以,
又平面平面,所以为二面角的平面角,
在中,,,,,所以,
在中,,,所以,
所以,
所以二面角的余弦值为.
第1页,共1页
数学试卷
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.若,,,则的值为( )
A. B. C. D.
2.已知是三个不同的平面,是两条不同的直线,则下列命题正确的是( )
A. 若,,则 B. 若,,则
C. 若,,则 D. 若,,则
3.如图,样本和分别取自两个不同的总体,它们的样本平均数分别为和,样本标准差分别为和,则( )
A. , B. ,
C. , D. ,
4.已知为随机事件,与互斥,与互为对立,且,则( )
A. B. C. D.
5.如图,在直三棱柱中,,点为的中点,则异面直线与所成的角为( )
A. B. C. D.
6.某兴趣小组有名男生和名女生,现从中选人参加公益活动,则至少选中一名女生的概率为( )
A. B. C. D.
7.已知的内角,,的对边分别为,,,且,,则面积的最大值为( )
A. B. C. D.
8.九章算术商功:“斜解立方,得两壍堵斜解壍堵,其一为阳马,一为鳖臑阳马居二,鳖臑居一,不易之率也合两鳖臑三而一,验之棊,其形露矣”即将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑如图所示为鳖臑,平面,,,分别在棱,上,且,若,则三棱锥外接球的体积为( )
A. B. C. D.
二、多选题:本题共4小题,共20分。在每小题给出的选项中,有多项符合题目要求。
9.某市天国庆节假期期间的楼房认购量单位:套与成交量单位:套的折线图如图所示,则以下说法错误的是( )
A. 成交量的中位数是 B. 日成交量超过日平均成交量的有天
C. 认购量越大,则成交量就越大 D. 认购量的第一四分位数是
10.已知事件,相互独立,且,,则( )
A. B.
C. D.
11.已知圆台的上、下底面半径分别为和,母线长为,则( )
A. 圆台的高为 B. 圆台的侧面积为
C. 圆台的体积为 D. 圆台的轴截面面积为
12.如图,正方体的棱长为,是侧面上的一个动点含边界,点在棱上,且,则下列结论正确的有( )
A. 平面被正方体截得截面为三角形
B. 若,直线
C. 若在上,的最小值为
D. 若,点 的轨迹长度为
三、填空题:本题共4小题,每小题5分,共20分。
13.某眼科医院为了了解高中学生的视力情况,利用分层抽样的方法从某高中三个年级中抽取了人进行问卷调查,其中高一年级抽取了人,高二年级抽取了人,且高三年级共有学生人,则该高中三个年级的学生总数为 人.
14.在正方体中,为的中点,则与平面所成角的正弦值为 .
15.甲、乙两支羽毛球队体检结果如下:甲队的体重的平均数为,方差为,乙队体重的平均数为,方差为,又已知甲、乙两队的队员人数之比为,那么甲、乙两队全部队员的方差等于 .
16.电路从到上共连接着个灯泡如图,每个灯泡断路的概率是,整个电路的连通与否取决于灯泡是否断路.则从到连通的概率是 .
四、解答题:本题共6小题,共72分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
在中,角,,的对边分别为,,,且,.
若,求的值;
若的面积为,求的值.
18.本小题分
如图所示,三棱柱,是的中点,是的中点.求证:
平面;
平面平面D.
19.本小题分
新高考实行“”选科模式,其中“”为必考科目,语文、数学、外语所有学生必考;“”为首选科目,从物理、历史中选择一科;“”为再选科目,从化学、生物学、地理、思想政治中任选两科某大学的某专业要求首选科目为物理,再选科目中化学、生物学至少选一科.
写出所有选科组合的样本空间从所有选科组合中随机选一种组合,并且每种组合被选到的可能性相等,求所选组合符合该大学某专业报考条件的概率;
甲、乙两位同学独立进行选科,求两人中至少有一人符合该大学某专业报考条件的概率.
20.本小题分
如图,四棱锥中,平面,四边形为梯形,,,,是上一点且,.
Ⅰ求证:平面;
Ⅱ求点到平面的距离.
21.本小题分
某校在一次期末数学测试中,为统计学生的考试情况,从学校的名学生中随机抽取名学生的考试成绩,被测学生成绩全部介于分到分之间满分分,将统计结果按如下方式分成八组:第一组,第二组,第八组,如图是按上述分组方法得到的频率分布直方图的一部分.
根据图表,计算第七组的频率,并估计该校的名学生这次考试成绩的平均分同一组中的数据用该组区间的中点值代表该组数据平均值;
若从样本成绩属于第六组和第八组的所有学生中随机抽取名,求他们的分差的绝对值小于分的概率.
22.本小题分
如图,在四棱锥中,平面,,且,是的中点.
证明:;
若,直线与直线所成角的余弦值为.
(ⅰ)求直线与平面所成角
(ⅱ)求二面角的余弦值.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14. 或
15.
16.
17.解:在中,,
,即.
,
则,
解得,
又,
,
.
18.证明:由题意,是三棱柱,
连接,与交于,连接,可得,
平面,平面,
平面D.
是的中点,是的中点,
,四边形为平行四边形,
,
又平面,平面,
平面,
由可知平面,
又,B、平面,
平面平面D.
19.解:依题意,样本空间为物化生,物化地,物化政,物生地,物生政,物地政,史化生,史化地,史化政,史生地,史生政,史地政,,
记事件“所选组合符合该大学某专业报考条件”,则物化生,物化地,物化政,物生地,物生政,,所以.
记事件“甲符合该大学某专业报考条件”,
事件“乙符合该大学某专业报考条件”,
事件“甲、乙两人中至少有一人符合该大学某专业报考条件”,
由可知,,
所以.
20.Ⅰ证明:平面,平面,
,
又,,、平面,
平面,又平面,
.
又平面,平面,
,
又,、平面,
平面,
Ⅱ解:由,且为梯形,,且,
则为菱形,所以,
由得,,又,所以,
则
从而有是边长为的等边三角形.
在中:,,
设到平面的距离为,
由得,
,
解得,
即到平面的距离为.
21.解:由频率分布直方图得第七组的频率为:
.
用样本数据估计该校的名学生这次考试成绩的平均分为:
.
样本成绩属于第六组的有人,设为,
样本成绩属于第八组的有人,设为,
从样本成绩属于第六组和第八组的所有学生中随机抽取名,
基本事件有:,,,,,,,,,共个
他们的分差的绝对值小于分,即在同一组中包含的基本事件有:,,,共个
他们的分差的绝对值小于分的概率.
22.解:取的中点,连接,,如图所示,
因为平面,平面,所以,
因为,所以,
平面,,所以平面,
因为平面,所以,
在中,因为,分别为,的中点,则,,
又,,所以,,所以四边形为平行四边形,
所以,
因为,所以.
连接,如图,
在中,,,所以,
因为,平面,平面,,所以平面,
因为平面,所以,
因为,所以与所成角与与所成角相等,
在中,,,所以,
所以,
由知平面,所以直线与平面所成角为,
在中,,所以,
所以直线与平面所成角为.
延长,交的延长线于,连结,如图所示,
取的中点,在中,过点作的垂线,垂足为,连接,
因为,,所以,
因为平面,平面,所以,
因为平面,平面,,所以平面,
因为平面,所以,
因为,平面,平面,,所以平面,
因为平面,所以,
又平面平面,所以为二面角的平面角,
在中,,,,,所以,
在中,,,所以,
所以,
所以二面角的余弦值为.
第1页,共1页
同课章节目录
