人教版数学八年级上暑假预习课第三讲 多边形及其内角和(含解析)
文档属性
| 名称 | 人教版数学八年级上暑假预习课第三讲 多边形及其内角和(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 13.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-26 10:08:44 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
人教版数学八年级上暑假预习课
第三讲 多边形及其内角和
一、专题导航
知识点梳理
知识点1 多边形
1.定义:在平面内不在同一直线上的一些线段首尾顺次相接所组成的封闭图形叫做多边形.其中,各个角相等、各条边相等的多边形叫做正多边形.
2.相关概念:
边:组成多边形的各条线段叫做多边形的边.
顶点:每相邻两条边的公共端点叫做多边形的顶点.
内角:多边形相邻两边组成的角叫多边形的内角,一个n边形有n个内角.
外角:多边形的边与它的邻边的延长线组成的角叫做多边形的外角.
对角线:连接多边形不相邻的两个顶点的线段,叫做多边形的对角线.
3. 多边形的分类:画出多边形的任何一边所在的直线,如果整个多边形都在这条直线的同一侧,那么这个多边形就是凸多边形,如果整个多边形不在直线的同一侧,这个多边形叫凹多边形.如图:
注意(1)正多边形必须满足两个条件(1)各边相等,各角相等。
(2)过多边形一个顶点有(n-3)条对角线。N边形共有条对角线
(3)过n边形一个顶点把n边形分成(n-2)个三角形。
典例剖析1
例1-1.在如图所示的图形中,属于多边形的有( )
A.2个 B.3个 C.4个 D.5个
例1-2.下列图形是正多边形的是( )
A. B. C. D.
例1-3.若一个多边形的一条对角线将其分成两个四边形,则该多边形的边数是 .
知识点2 多边形的内角和
n边形的内角和定理:n边形的内角和为(n 2) 180°
典例剖析2
例2-1.一个八边形的内角和是( )
A. B. C. D.
例2-2.如果从某个多边形的一个顶点出发的对角线共有6条,那么该多边形的内角和是( )
A. B. C. D.
例2-3.如图,的度数为
例2-4.如图,正六边形,正方形,连接,则图中的度数为 .
知识点3 多边形的外角和
1.n边形的外角和定理:多边形的外角和等于360°(与多边形的形状和边数无关)。
2.平面镶嵌:平面镶嵌是指用形状、大小完全相同的一种或几种平面图形进行拼接,彼此之间不留空隙、不重叠地铺成一片,平面镶嵌又称为平面密铺、“平面图形的镶嵌”。
典例剖析3
例3-1.小聪利用所学的数学知识,给同桌出了这样一道题:假如从点A出发,沿直线走9米后向左转,接着沿直线前进9米后,再向左转,…,如此下去,当他第一次回到点A时,发现自己一共走了72米,则的度数为( )
A. B. C. D.
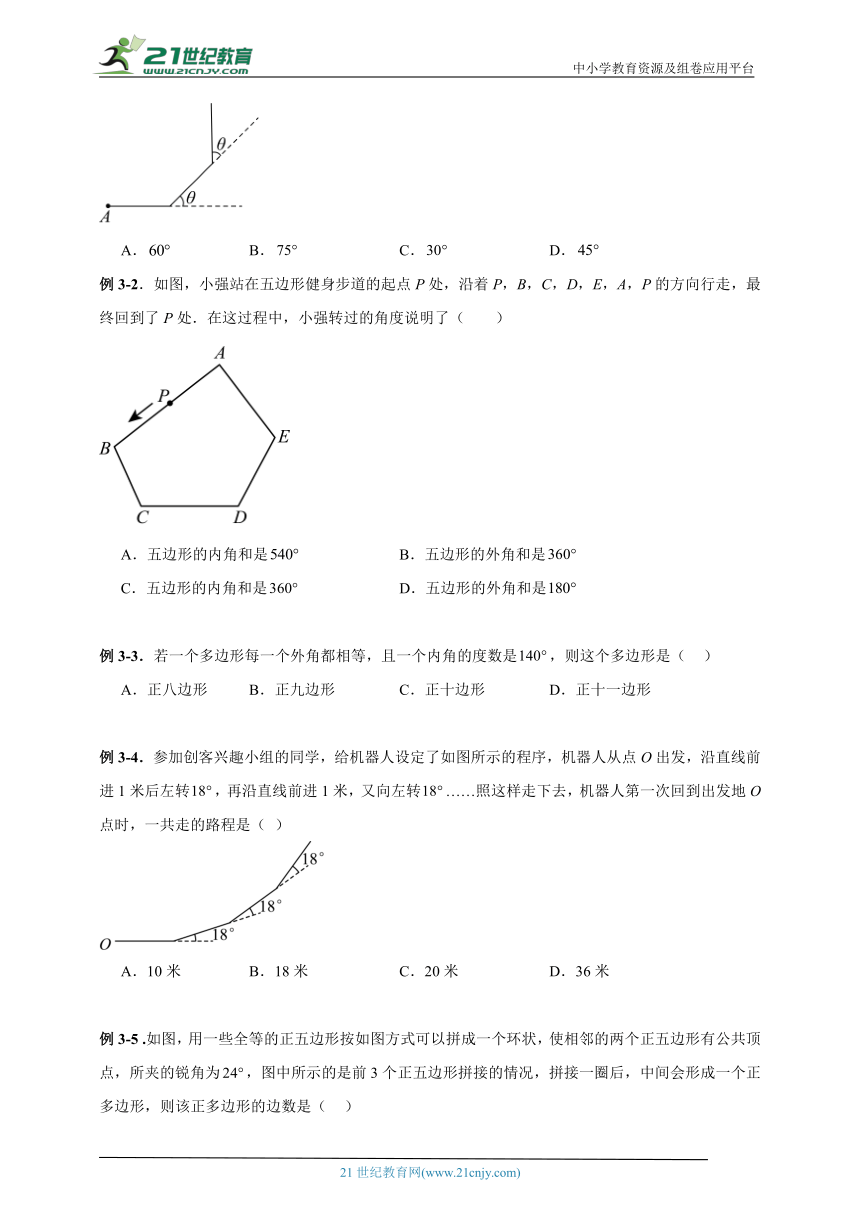
例3-2.如图,小强站在五边形健身步道的起点P处,沿着P,B,C,D,E,A,P的方向行走,最终回到了P处.在这过程中,小强转过的角度说明了( )
A.五边形的内角和是 B.五边形的外角和是
C.五边形的内角和是 D.五边形的外角和是
例3-3.若一个多边形每一个外角都相等,且一个内角的度数是,则这个多边形是( )
A.正八边形 B.正九边形 C.正十边形 D.正十一边形
例3-4.参加创客兴趣小组的同学,给机器人设定了如图所示的程序,机器人从点O出发,沿直线前进1米后左转,再沿直线前进1米,又向左转……照这样走下去,机器人第一次回到出发地O点时,一共走的路程是( )
A.10米 B.18米 C.20米 D.36米
例3-5 .如图,用一些全等的正五边形按如图方式可以拼成一个环状,使相邻的两个正五边形有公共顶点,所夹的锐角为,图中所示的是前3个正五边形拼接的情况,拼接一圈后,中间会形成一个正多边形,则该正多边形的边数是( )
A.4 B.5 C.6 D.7
变式训练
变式训练1 多边形
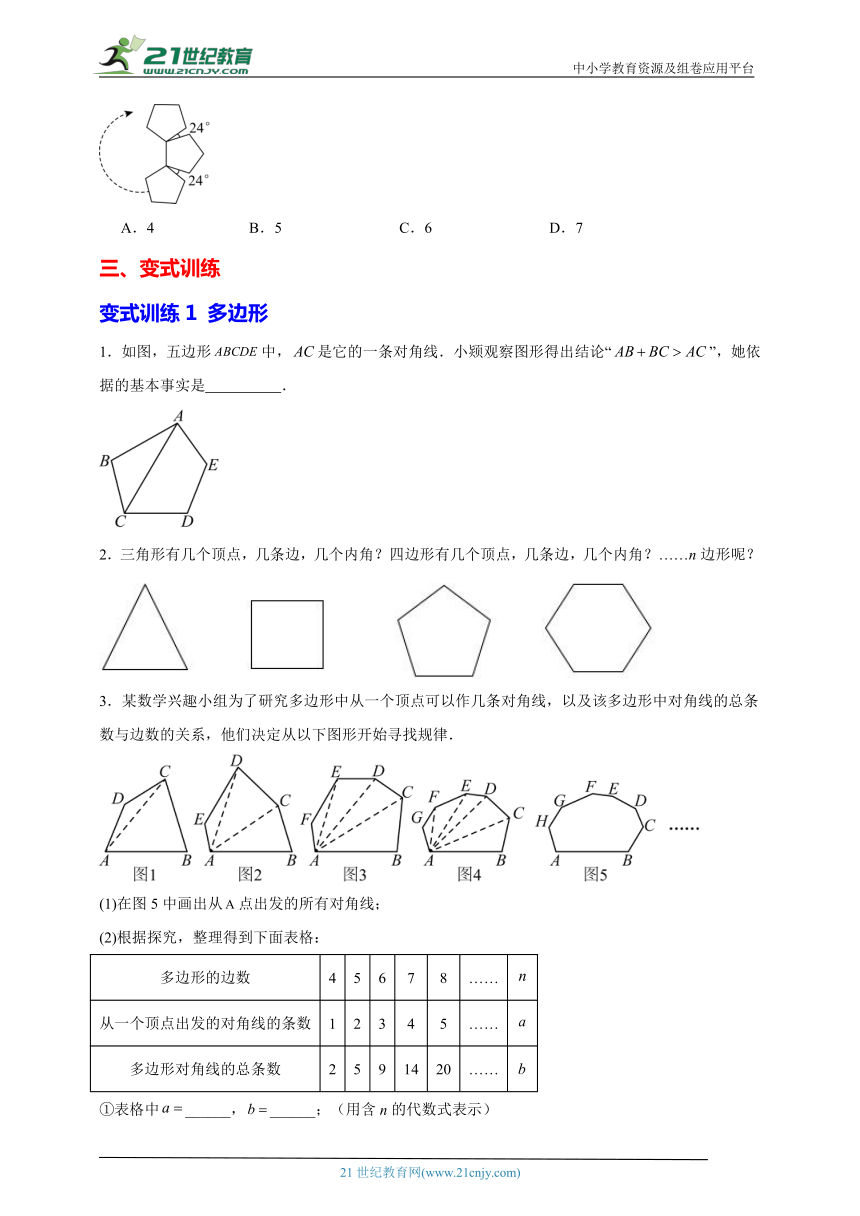
1.如图,五边形中,是它的一条对角线.小颎观察图形得出结论“”,她依据的基本事实是 .
2.三角形有几个顶点,几条边,几个内角?四边形有几个顶点,几条边,几个内角?……n边形呢?
3.某数学兴趣小组为了研究多边形中从一个顶点可以作几条对角线,以及该多边形中对角线的总条数与边数的关系,他们决定从以下图形开始寻找规律.
(1)在图5中画出从点出发的所有对角线;
(2)根据探究,整理得到下面表格:
多边形的边数 4 5 6 7 8 ……
从一个顶点出发的对角线的条数 1 2 3 4 5 ……
多边形对角线的总条数 2 5 9 14 20 ……
①表格中______,______;(用含n的代数式表示)
②拓展应用:
若该校要举办足球比赛,总共有个班级参加比赛,规定每个班级都要和其他班级比赛一次,请计算总共要比赛多少场.
变式训练2 多边形的内角和
1.小明在计算一个多边形的内角和时,漏掉了一个内角,结果算得,则这个内角的度数为 .
2.如图,正八边形的对角线,交于点,则的度数是 .
3.小宇阅读了一篇《东方窗棂之美》的文章,文章中有一张如图所示的图片,图中有许多不规则的多边形组成,代表一种自然和谐美.如图是从图图案中提取的由六条线段组成的图形,若,则的度数是 .
变式训练3多边形的外角
1.如果你可以只用一种图形没有重叠、没有间隙地铺满一个平面,那么这种图形就被称为可以“镶嵌”这个平面,完美五边形就是这种图形.如图的五边形是迄今为止人类发现的第15种完美五边形.若度,则 度.
2.如图,七边形中,,的延长线交于点,若,,,的外角和等于,则的度数为 .
3.(1)如图①,都是四边形的外角,试探究,与之间的数量关系;
(2)如图②,都是四边形的外角,试探究与之间的数量关系;
(3)用你发现的结论解决下列问题∶如图③,分别是四边形的外角、的平分线,,求的度数.
4.【教材呈现】根据如图所示的华师版七年级下册教材第77页部分内容,解答下列问题.
如图9.1.9,一个三角形的每一个外角对应一个相邻的内角和两个不相邻的内角.三角形的外角与内角有什么关系呢?在图9.1.10中,显然有(外角)(相邻的内角)那么外角与其他两个不相邻的内角又有什么关系呢?
如图1,请写出与、之间的数量关系,并给出证明.
【拓展延伸】七年级某数学兴趣小组学习了关于三角形外角的性质后,提出问题:四边形的一个外角与它不相邻的三个内角之间具有怎样的数量关系?如图2,已知是四边形的一个外角,直接写出与的数量关系为:______.
【应用提升】如图3,为四边形的一个外角,平分交的角平分线于点F,若,则______°.
5.如图,一个正方形水池的四周恰好被4个正n边形地板铺满,则 .
6.如图所示的地面由正五边形和正n边形两种地砖镶嵌而成,则的度数为 °.
能力提升
多边形
1.同学们,你们会用画多边形的对角线来解决生活中的数学问题吗?
比如,学校举办足球赛,共有5个班级的足球队参加比赛,每个队都要和其他各队比赛一场,根据积分排列名次.问学校一共要安排多少场比赛?
我们画出5个点,每个点各代表一个足球队,两个队之间比赛一场就用一条线段把它们连接起来.由于每个队都要与其他各队比赛一场,这样每个点与另外4个点都会有一条线段连接(如图).
现在我们只要数一数五边形的边数和它的对角线条数就可以了.由图可知,五边形的边数和对角线条数都是5,所以学校一共要安排10场比赛.
同学们,请用类似的方法来解决下面的问题:
姣姣、林林、可可、飞飞、红红和娜娜六人参加一次会议,见面时他们相互握手问好.已知姣姣已握了5次手,林林已握了4次手,可可已握了3次手,飞飞已握了2次手,红红握手1次,请推算出娜娜目前已和哪几个人握了手.
2.连接多边形不相邻的两个顶点的线段,叫做多边形的对角线,如图(1),、是五边形的对角线.思考下列问题:
(1)如图(2),边形中,过顶点可以画 条对角线,它们分别是 ;过顶点可以画 条对角线,过顶点可以画 条对角线.
(2)过顶点的对角线与过顶点的对角线有相同的吗?过顶点的对角线与过顶点的对角线有相同的吗?
(3)在此基础上,你能发现边形的对角线条数的规律吗?
多边形的内角和
1.在中,.点D、E分别在的边上,且均不与的顶点重合,连接,将沿折叠,使点A的对称点始终落在四边形的外部,交边于点F,且点与点C在直线的异侧.
(1)如图①,则_______.
(2)如图②,则_______.
(3)如图③,设图②中的.求的度数;
(4)当的某条边与或垂直时,直接写出的度数.
2.一个多边形纸片剪去一个内角后,得到一个内角和为2340°的新多边形,求原多边形的边数.
3.阅读材料:
如图1,AB、CD交于点O,我们把△AOD和△BOC叫做对顶三角形.
结论:若△AOD和△BOC是对顶三角形,则∠A+∠D=∠B+∠C.
结论应用举例:
如图2:求五角星的五个内角之和,即∠A+∠B+∠ACE+∠ADB+∠E的度数.
解:连接CD,由对顶三角形的性质得:∠B+∠E=∠1+∠2,
在△ACD中,∵∠A+∠ACD+∠ADC=180°,
即∠A+∠3+∠1+∠2+∠4=180°,
∴∠A+∠ACE+∠B+∠E+ADB=180°
即五角星的五个内角之和为180°.
解决问题:
(1)如图①,∠A+∠B+∠C+∠D+∠E+∠F= ;
(2)如图②,∠A+∠B+∠C+∠D+∠E+∠F+∠G= ;
(3)如图③,∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H= ;
(4)如图④,∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠M+∠N= ;
请你从图③或图④中任选一个,写出你的计算过程.
4.(1)如图①,求∠A+∠B+∠C+∠D+∠E+∠F的度数;
(2)如图②,求∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H的度数;
(3)如图③,求∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数.
多边形的外角
1.在五边形ABCDE中,,,.
(1)如图①,画出五边形ABCDE的所有对角线;
(2)如图②,若比小,求出的度数;
(3)如图③,若CP,DP分别平分与的外角,试求出的度数.
2.已如在四边形中,.
(1)如图1,若,则________.
(2)如图2,若、分别平分、,判断与位置关系并证明理由.
(3)如图3,若、分别五等分、(即,),则_______.
3.如图,四边形ABCD中,AD∥BC,∠BDC=∠BCD,DE⊥DC交AB于E.
(1)求证:DE平分∠ADB;
(2)若∠ABD的平分线与CD的延长线交于F,设∠F=α.
①若α=50°,求∠A的值;
②若∠F<,试确定α的取值范围.
4.四边形ABCD中,∠A=145°,∠D=75°.
(1)如图1,若∠B=∠C,试求出∠C的度数;
(2)如图2,若∠ABC的角平分线BE交DC于点E,且BE∥AD,试求出∠C的度数;
(3)①如图3,若∠ABC和∠BCD的角平分线交于点E,试求出∠BEC的度数.
②在①的条件下,若延长BA、CD交于点F(如图4),将原来条件“∠A=145°,∠D=75°”改为“∠F=40°”,其他条件不变,∠BEC的度数会发生变化吗?若不变,请说明理由;若变化,求出∠BEC的度数.
5.用地砖铺地,用瓷砖贴墙,都要求砖与砖严丝合缝,不留空隙,把地面或墙面全部覆盖.从数学角度看,这些工作就是用一些不重叠摆放的多边形把平面的一部分完全覆盖,通常把这类问题叫做用多边形覆盖平面(或平面镶嵌)的问题.
(1)如图1是铺在某知名大学数学系大楼入口的彭罗斯地砖,它由如图2和如图3所示的两种不同菱形镶嵌而成.
请观察图形,并填空:______°,______°;
(2)如图4所示的拼合图案是使用全等的正三角形地砖铺成.类似的,单独使用哪几种全等的正多边形能镶嵌成一个平面图案?请证明你的结论;
(3)我们也可以用边长相等的多种正多边形镶嵌平面.如果镶嵌时某个顶点处的正多边形有m个,设这m个正多边形的边数分别为,,…,,请说明m与,,…,应满足什么关系?当时,写出所有满足条件的正多边形的组合.
人教版数学八年级上暑假预习课
第三讲 多边形及其内角和
一、专题导航
二、知识点梳理
知识点1 多边形
1.定义:在平面内不在同一直线上的一些线段首尾顺次相接所组成的封闭图形叫做多边形.其中,各个角相等、各条边相等的多边形叫做正多边形.
2.相关概念:
边:组成多边形的各条线段叫做多边形的边.
顶点:每相邻两条边的公共端点叫做多边形的顶点.
内角:多边形相邻两边组成的角叫多边形的内角,一个n边形有n个内角.
外角:多边形的边与它的邻边的延长线组成的角叫做多边形的外角.
对角线:连接多边形不相邻的两个顶点的线段,叫做多边形的对角线.
3. 多边形的分类:画出多边形的任何一边所在的直线,如果整个多边形都在这条直线的同一侧,那么这个多边形就是凸多边形,如果整个多边形不在直线的同一侧,这个多边形叫凹多边形.如图:
注意(1)正多边形必须满足两个条件(1)各边相等,各角相等。
(2)过多边形一个顶点有(n-3)条对角线。N边形共有条对角线
(3)过n边形一个顶点把n边形分成(n-2)个三角形。
典例剖析1
例1-1.在如图所示的图形中,属于多边形的有( )
A.2个 B.3个 C.4个 D.5个
【答案】C
【分析】本题考查多边形定义,根据多边形定义,逐个验证即可得到答案.
【详解】解:所示的图形中,第一个是三角形、第二个是四边形、第三个是圆、第四个是正六边形、第五个是正方体,
是多边形的有第一个、第二个、第四个,共有3个,
故选:C.
例1-2.下列图形是正多边形的是( )
A. B. C. D.
【答案】C
【分析】本题主要考查了正多边形,根据正多边形的定义;各个角都相等,各条边都相等的多边形叫做正多边形可得答案.
【详解】解:A.是等腰三角形,不是正多边形,故选项A不符合题意;
B.是圆角矩形,不是正多边形,故选项B不符合题意;
C.是正五边形,符合题意;
D.是一般六边形,不是正多边形,故选项D不符合题意;
故选:C.
例1-3.若一个多边形的一条对角线将其分成两个四边形,则该多边形的边数是 .
【答案】六/
【分析】本题考查了多边形的对角线,根据一个多边形被一条对角线分成两个四边形,可得多边形的边数,可得答案.
【详解】解:两个四边形有一条公共边,得多边形边的数目是,
故答案为:六.
知识点2 多边形的内角和
n边形的内角和定理:n边形的内角和为(n 2) 180°
典例剖析2
例2-1.一个八边形的内角和是( )
A. B. C. D.
【答案】A
【分析】本题考查了多边形的内角和,熟记内角和公式是解题的关键.根据多边形的内角和公式,列式进行计算即可得解.
【详解】解:.
故选: A
例2-2.如果从某个多边形的一个顶点出发的对角线共有6条,那么该多边形的内角和是( )
A. B. C. D.
【答案】D
【分析】本题考查了多边形的内角和公式,多边形的对角线的公式,求出多边形的边数是解题的关键.
根据从n边形的一个顶点可以作对角线的条数为条,求出边数,然后根据多边形的内角和公式,列式进行计算即可得解.
【详解】多边形从一个顶点出发可引出6条对角线,
,
解得:,
内角和,
故选:D.
例2-3.如图,的度数为
【答案】
【分析】此题主要考查了复杂图形角的和.熟练掌握三角形外角性质,四边形内角和定理,是解决问题的关键.
根据三角形外角的性质,,四边形内角和等于,可得的度数.
【详解】如图,
,
,
,
故答案为:.
例2-4.如图,正六边形,正方形,连接,则图中的度数为 .
【答案】/15度
【分析】本题考查了正多边形的内角,等腰三角形的判定即性质,熟悉掌握正多边形的内角运算方法是解题的关键.
利用正多边形的内角度数求法运算出正六边形和正方形的内角度数,即可得到的度数,再利用等腰三角形的性质运算求解即可.
【详解】解:∵正六边形的内角度数为:,正方形的内角度数为:,
∴,,
∴,
∵,
∴,
故答案为:.
知识点3 多边形的外角和
1.n边形的外角和定理:多边形的外角和等于360°(与多边形的形状和边数无关)。
2.平面镶嵌:平面镶嵌是指用形状、大小完全相同的一种或几种平面图形进行拼接,彼此之间不留空隙、不重叠地铺成一片,平面镶嵌又称为平面密铺、“平面图形的镶嵌”。
典例剖析3
例3-1.小聪利用所学的数学知识,给同桌出了这样一道题:假如从点A出发,沿直线走9米后向左转,接着沿直线前进9米后,再向左转,…,如此下去,当他第一次回到点A时,发现自己一共走了72米,则的度数为( )
A. B. C. D.
【答案】D
【分析】本题考查了多边形的内角与外角,解决本题的关键是明确第一次回到出发点A时,所经过的路线正好构成一个正多边形.第一次回到出发点A时,所经过的路线正好构成一个正多边形,用,求得边数,再根据多边形的外角和为,即可求解.
【详解】解:∵第一次回到出发点A时,所经过的路线正好构成一个正多边形,
∴正多边形的边数为:,
根据多边形的外角和为,
∴则他每次转动θ的角度为:,
故选:D.
例3-2.如图,小强站在五边形健身步道的起点P处,沿着P,B,C,D,E,A,P的方向行走,最终回到了P处.在这过程中,小强转过的角度说明了( )
A.五边形的内角和是 B.五边形的外角和是
C.五边形的内角和是 D.五边形的外角和是
【答案】B
【分析】本题主要考查多边形的内角和外角.根据题意可知小强转过的角度之和正好是五边形的外角和,再根据多边形的外角和性质即可得出答案.
【详解】解:小强转过的角度之和正好是五边形的外角和,
小强转过的角度之和为.
故选:B.
例3-3.若一个多边形每一个外角都相等,且一个内角的度数是,则这个多边形是( )
A.正八边形 B.正九边形 C.正十边形 D.正十一边形
【答案】B
【分析】本题考查了正多边形的外角与外角和的关系,需要熟练掌握并灵活运用.
先根据平角的定义求出每一个外角的度数,再根据边数外角度数计算即可.
【详解】解:,
,
这个多边形是正九边形.
故选:B.
例3-4.参加创客兴趣小组的同学,给机器人设定了如图所示的程序,机器人从点O出发,沿直线前进1米后左转,再沿直线前进1米,又向左转……照这样走下去,机器人第一次回到出发地O点时,一共走的路程是( )
A.10米 B.18米 C.20米 D.36米
【答案】C
【分析】本题考查了多边形的外角和定理的应用.由题意可知小华所走的路线为一个正多边形,根据多边形的外角和即可求出答案.
【详解】解:∵,
∴他需要走20次才会回到原来的起点,
即一共走了(米).
故选:C
例3-5 .如图,用一些全等的正五边形按如图方式可以拼成一个环状,使相邻的两个正五边形有公共顶点,所夹的锐角为,图中所示的是前3个正五边形拼接的情况,拼接一圈后,中间会形成一个正多边形,则该正多边形的边数是( )
A.4 B.5 C.6 D.7
【答案】C
【分析】本题考查了正多边形、多边形的内角与外角等知识;由完全拼成一个圆环需要的正五边形为个,则围成的多边形为正边形,利用正五边形的内角与夹角计算出正边的每个内角的度数,然后根据内角和定理得到解方程求解即可.
【详解】∵正五边形的每个内角为,
∴组成的正多边形的每个内角为,
∵n个全等的正五边形拼接可以拼成一个环状,中间会形成一个正多边形,
∴形成的正多边形为正n边形,则,
解得:.
故选C.
三、变式训练
变式训练1 多边形
1.如图,五边形中,是它的一条对角线.小颎观察图形得出结论“”,她依据的基本事实是 .
【答案】两点之间线段最短
【分析】本题考查线段的性质,根据两点之间,线段最短,进行作答即可.
【详解】解:依据的基本事实是:两点之间线段最短;
故答案为:两点之间线段最短.
2.三角形有几个顶点,几条边,几个内角?四边形有几个顶点,几条边,几个内角?……n边形呢?
【答案】见解析
【分析】根据图形的特征作答即可.
【详解】解:如图所示,三角形有3个顶点,3条边,3个内角;
四边形有4个顶点,4条边,4个内角;
五边形有5个顶点,5条边,5个内角;
……
可发现,多边形的顶点个数和内角个数与边数相同;
n边形有n个顶点,n条边,n个内角.
【点睛】本题考查了多边形的有关概念,解题关键是准确识别多边形,明确多边形的顶点和内角概念.
3.某数学兴趣小组为了研究多边形中从一个顶点可以作几条对角线,以及该多边形中对角线的总条数与边数的关系,他们决定从以下图形开始寻找规律.
(1)在图5中画出从点出发的所有对角线;
(2)根据探究,整理得到下面表格:
多边形的边数 4 5 6 7 8 ……
从一个顶点出发的对角线的条数 1 2 3 4 5 ……
多边形对角线的总条数 2 5 9 14 20 ……
①表格中______,______;(用含n的代数式表示)
②拓展应用:
若该校要举办足球比赛,总共有个班级参加比赛,规定每个班级都要和其他班级比赛一次,请计算总共要比赛多少场.
【答案】(1)见解析
(2)①,;②场
【分析】本题考查了多边形的对角线,根据表格信息寻求规律是解题的关键.
(1)连接作图即可;
(2)①根据所给数据规律解答即可;
②根据每班都需要和对手比赛一次,且一次比赛能满足2个班级的比赛需求列式运算即可.
【详解】(1)如图所示,即为所求;
(2)解:①,;
②(场),
答:共需要比赛场.
变式训练2 多边形的内角和
1.小明在计算一个多边形的内角和时,漏掉了一个内角,结果算得,则这个内角的度数为 .
【答案】/100度
【分析】设这个多边形的边数是n,根据漏掉的那个内角的范围介于可得关于n的不等式组,求出n的范围结合n为正整数即得答案.
【详解】解析:设这个多边形的边数是n,
依题意,得,
解得.
又n为正整数,
∴.
∴这个内角的度数为.
故答案为:.
【点睛】本题考查了多边形的内角和,正确理解题意、求出n的范围是关键.
2.如图,正八边形的对角线,交于点,则的度数是 .
【答案】
【分析】本题主要考查多边形内角和外角,先求出,再根据正八边形的性质求出和,最后根据三角形的内角和即可求得.
【详解】解:∵八边形为正八边形,
∵,
∵正八边形的对角线,
∴,
又,
∴,
∴.
故答案为:67.5.
3.小宇阅读了一篇《东方窗棂之美》的文章,文章中有一张如图所示的图片,图中有许多不规则的多边形组成,代表一种自然和谐美.如图是从图图案中提取的由六条线段组成的图形,若,则的度数是 .
【答案】/300度
【分析】本题考查了多边形的外角,根据外角和为即可求解.
【详解】多边形的外角和等于
故答案为:.
变式训练3多边形的外角
1.如果你可以只用一种图形没有重叠、没有间隙地铺满一个平面,那么这种图形就被称为可以“镶嵌”这个平面,完美五边形就是这种图形.如图的五边形是迄今为止人类发现的第15种完美五边形.若度,则 度.
【答案】285
【分析】本题考查多边形的外角和,根据多边形的外角和为360度,进行求解即可.
【详解】解:由题意,得:,
∵度,
∴;
故答案为:285
2.如图,七边形中,,的延长线交于点,若,,,的外角和等于,则的度数为 .
【答案】/40度
【分析】本题考查了多边形内角和问题,熟练掌握多边形的内角和等于是解题的关键.根据题意计算,,,的度数之和,再计算五边形的内角和,即可求解.
【详解】解:,,,的外角和等于,
,
五边形的内角和为,
.
故答案为:.
3.(1)如图①,都是四边形的外角,试探究,与之间的数量关系;
(2)如图②,都是四边形的外角,试探究与之间的数量关系;
(3)用你发现的结论解决下列问题∶如图③,分别是四边形的外角、的平分线,,求的度数.
【答案】(1);(2);(3)
【分析】本题考查了多边形的内角和公式,平角的定义,角平分线的定义,整体思想的利用是解题的关键.
(1)根据四边形的内角和等于表示出,再根据平角的定义用表示出,即可得解;
(2)从外角的定义考虑解答;
(3)根据(1)、(2)的结论求出,再根据角平分线的定义求出,然后利用三角形的内角和定理列式进行计算即可得解.
【详解】(1)∵,
,
,,
,
;
(2)∵,
,
,,
,
,
(3),
根据(1)和(2)的结论有:,
分别是的平分线,
,,
,
.
4.【教材呈现】根据如图所示的华师版七年级下册教材第77页部分内容,解答下列问题.
如图9.1.9,一个三角形的每一个外角对应一个相邻的内角和两个不相邻的内角.三角形的外角与内角有什么关系呢?在图9.1.10中,显然有(外角)(相邻的内角)那么外角与其他两个不相邻的内角又有什么关系呢?
如图1,请写出与、之间的数量关系,并给出证明.
【拓展延伸】七年级某数学兴趣小组学习了关于三角形外角的性质后,提出问题:四边形的一个外角与它不相邻的三个内角之间具有怎样的数量关系?如图2,已知是四边形的一个外角,直接写出与的数量关系为:______.
【应用提升】如图3,为四边形的一个外角,平分交的角平分线于点F,若,则______°.
【答案】(教材呈现),证明见解析;(拓展延伸);(应用提升)
【分析】本题考查三角形与四边形的内角和,三角形的外角,角平分线的定义.
(教材呈现)根据三角形的内角和定理与邻补角互补即可解答;
(拓展延伸)根据四边形的内角和定理与邻补角互补即可解答;
(应用提升)由(教材呈现)可知,由角平分线的定义可得,,又由(拓展延伸)可知,从而,化简即可解答.
【详解】解:(教材呈现)
,
证明:∵,,
∴;
(拓展延伸)
∵,,
∴,
∵,
∴,
故答案为:;
(应用提升)
由(教材呈现)可知
∵平分,平分
∴,,
由(拓展延伸)可知,
∴,
∴,
∴.
故答案为:
5.如图,一个正方形水池的四周恰好被4个正n边形地板铺满,则 .
【答案】8
【分析】本题考查学生对平面镶嵌知识的掌握情况,体现了学数学用数学的思想,同时考查了多边形的内角和公式.根据平面镶嵌的条件,先求出正n边形的一个内角的度数,再根据内角和公式求出n的值.
【详解】解:正n边形的一个内角,
则,
解得,
故答案为:8.
6.如图所示的地面由正五边形和正n边形两种地砖镶嵌而成,则的度数为 °.
【答案】
【分析】本题考查了正多边形的内角和公式,掌握正多边形的概念,数形结合是解题的关键.先计算出正五边形的内角,再根据平面镶嵌的条件计算求解.
【详解】正五边形的内角和为,
每个内角为,
∴,
故答案为:.
四、能力提升
多边形
1.同学们,你们会用画多边形的对角线来解决生活中的数学问题吗?
比如,学校举办足球赛,共有5个班级的足球队参加比赛,每个队都要和其他各队比赛一场,根据积分排列名次.问学校一共要安排多少场比赛?
我们画出5个点,每个点各代表一个足球队,两个队之间比赛一场就用一条线段把它们连接起来.由于每个队都要与其他各队比赛一场,这样每个点与另外4个点都会有一条线段连接(如图).
现在我们只要数一数五边形的边数和它的对角线条数就可以了.由图可知,五边形的边数和对角线条数都是5,所以学校一共要安排10场比赛.
同学们,请用类似的方法来解决下面的问题:
姣姣、林林、可可、飞飞、红红和娜娜六人参加一次会议,见面时他们相互握手问好.已知姣姣已握了5次手,林林已握了4次手,可可已握了3次手,飞飞已握了2次手,红红握手1次,请推算出娜娜目前已和哪几个人握了手.
【答案】姣姣、林林和可可三人已与娜娜握过手
【分析】本题考查了多边形的对角线的问题,解题的关键是将实际问题与数学问题有机的结合起来.
先画出6个点,A、、、、、各个点依次代表姣姣、林林、可可、飞飞、红红和娜娜,凡是两人之间握过手,就把代表他们的这两点用1条线段连接起来即可得到答案.
【详解】解:先画出6个点,A、、、、、各个点依次代表姣姣、林林、可可、飞飞、红红和娜娜,凡是两人之间握过手,就把代表他们的这两点用1条线段连接起来(如图所示).
先看姣姣(A)和红红(E).姣姣已握手5次,说明姣姣与另外5人都握了手,因此代表姣姣的A点与、、、、这5点都有一条线段连接;红红握手1次,他只能是与姣姣握的手了,所以点只能与A点之间有线段连接,与其它各点再也不能有线段连接了.
其次分析林林(B).林林已握手4次,由于他没有可能与红红握过手,所以只能是与剩下的四个人姣姣、可可、飞飞和娜娜握过手了,因此,点与A、、、四点之间有线段连接.
再看飞飞(D).飞飞已握手2次,而代表飞飞的点已与A、两点有线段连接了,所以点与其它的点不能再有线段连接了.
最后考察可可(C).可可与3人握了手,但已不能是与飞飞和红红握的手了,所以代表可可得点只能与A、、三点有线段连接.
现在观察图形,与代表娜娜的点连接的线段有3条、和,这说明姣姣、林林和可可三人已与娜娜握过手.
2.连接多边形不相邻的两个顶点的线段,叫做多边形的对角线,如图(1),、是五边形的对角线.思考下列问题:
(1)如图(2),边形中,过顶点可以画 条对角线,它们分别是 ;过顶点可以画 条对角线,过顶点可以画 条对角线.
(2)过顶点的对角线与过顶点的对角线有相同的吗?过顶点的对角线与过顶点的对角线有相同的吗?
(3)在此基础上,你能发现边形的对角线条数的规律吗?
【答案】(1),,,
(2)过点的和过点的没有重复的,但和过点的有重复的和重复)
(3)边形的对角线条数的为
【分析】此题考查了多边形的对角线的知识.
(1)过点和任意不相邻的两点连接可得出到一条对角线;同理可得过点、的情况.
(2)过点的和过点的没有重复的,但和过点的有重复的和重复);
(3)过每一点有条对角线,除去重复的即可得出总对角线的条数.
【详解】(1)解:过顶点可以画条对角线,它们分别是;
过顶点可以画条对角线,
过顶点可以画条对角线;
故答案为:,,,;
(2)解:过点的和过点的没有重复的,但和过点的有重复的和重复);
(3)解:边形的一个顶点不能与它本身及左右两个邻点相连成对角线,故可连出条,
共有个顶点,应为条,这样算出的数,正好多出了一倍,所以再除以2.
即边形的对角线条数的为.
多边形的内角和
1.在中,.点D、E分别在的边上,且均不与的顶点重合,连接,将沿折叠,使点A的对称点始终落在四边形的外部,交边于点F,且点与点C在直线的异侧.
(1)如图①,则_______.
(2)如图②,则_______.
(3)如图③,设图②中的.求的度数;
(4)当的某条边与或垂直时,直接写出的度数.
【答案】(1)48
(2)222
(3)
(4)或
【分析】本题考查的是三角形内角和定理,四边形的内角和定理,平行的性质和折叠的性质,熟悉相关性质并能熟练应用是解题的关键.
(1)根据三角形内角和定理可得的度数;
(2)根据四边形内角和定理可得的度数;
(3)由(2)的结论可得,由折叠可得,由三角形内角和定理可得,两式相减,可得答案;
(4)分两种情况:或或时,分别求解即可.
【详解】(1)解:,
故答案为:48;
(2)解:,
,
故答案为:222;
(3)解:由(2)知,
,
由折叠知,
,
,
得:;
(4)解:如图,当时,
,
,
,
由(3)知,
,
由折叠知,
;
如图,当时,
;
如图,当时,点与点C在直线的同侧,不合题意;
综上可知,的度数为或.
2.一个多边形纸片剪去一个内角后,得到一个内角和为2340°的新多边形,求原多边形的边数.
【答案】14或15或16.
【分析】根据多边形内角和公式,可得新多边形的边数;由剪去一个内角可分为三种情况:①截线都不经过顶点;②截线一端经过顶点;③截线两端都经过顶点;进行分类讨论,即可得到原来的边数.
【详解】解:根据题意,得
,
解得:,
新多边形的边数为15;
①如图,当截线都不经过顶点时,新多边形的边数比原来的多边形的边数多1,则
原多边形的边数为:;
②如图,当截线一端经过顶点时,新多边形的边数等于原来的多边形的边数,则
原多边形的边数为:15;
③如图,当截线两端都经过顶点时,新多边形的边数比原来的多边形的边数少1,则
原多边形的边数为:;
综合上述,原多边形的边数为:14或15或16.
【点睛】此题主要考查了多边形的内角和定理的应用,要熟练掌握,解答此题的关键是先求出新多边形的边数,然后根据剪去一个内角的方法进行分类讨论,从而得到答案.
3.阅读材料:
如图1,AB、CD交于点O,我们把△AOD和△BOC叫做对顶三角形.
结论:若△AOD和△BOC是对顶三角形,则∠A+∠D=∠B+∠C.
结论应用举例:
如图2:求五角星的五个内角之和,即∠A+∠B+∠ACE+∠ADB+∠E的度数.
解:连接CD,由对顶三角形的性质得:∠B+∠E=∠1+∠2,
在△ACD中,∵∠A+∠ACD+∠ADC=180°,
即∠A+∠3+∠1+∠2+∠4=180°,
∴∠A+∠ACE+∠B+∠E+ADB=180°
即五角星的五个内角之和为180°.
解决问题:
(1)如图①,∠A+∠B+∠C+∠D+∠E+∠F= ;
(2)如图②,∠A+∠B+∠C+∠D+∠E+∠F+∠G= ;
(3)如图③,∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H= ;
(4)如图④,∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠M+∠N= ;
请你从图③或图④中任选一个,写出你的计算过程.
【答案】(1)360°;(2)540°;(3)720°;(4)1080°;过程见解析
【分析】(1)连接CD,由对顶角三角形可得∠A+∠B=∠BDC+∠ACD,再由四边形的内角和定理得出结论;
(2)连接ED,由对顶角三角形可得∠A+∠B=∠BED+∠ADE,再由五边形的内角和定理得出结论;
(3)连接BH、DE,由对顶角三角形可知∠EBH+∠BHD=∠HDE+∠BED,再根据五边形的内角和定理得出结论;
(4)连接ND、NE,由对顶角三角形可知∠1+∠2=∠NGH+∠EHG,再由六边形的内角和定理得出结论.
【详解】解:(1)连接CD,由对顶角三角形可得∠A+∠B=∠BDC+∠ACD,则∠A+∠B+∠C+∠D+∠E+∠F=360°;
(2)连接ED,由对顶角三角形可得∠A+∠B=∠BED+∠ADE,则∠A+∠B+∠C+∠D+∠E+∠F+∠G=540°;
(3)连接BH、DE,
∵由对顶角三角形可知∠EBH+∠BHD=∠HDE+∠BED,
∴∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H=五边形CDEFG的内角和+△ABH的内角和=540°+180°=720°;
(4)连接ND、NE,
∵由对顶角三角形可知∠1+∠2=∠NGH+∠EHG,
∴∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠M+∠N=六边形BCFGHM的内角和+△AND的内角和+△NDE的内角和=(6-2)×180°+360°=1080°.
故答案为:360°;540°;720°;1080°.
【点睛】本题考查的是三角形内角和定理,根据题意作出辅助线,利用△AOD和△BOC叫做对顶三角形的性质及多边形的内角和定理解答是解答此题的关键.
4.(1)如图①,求∠A+∠B+∠C+∠D+∠E+∠F的度数;
(2)如图②,求∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H的度数;
(3)如图③,求∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数.
【答案】(1)360°;(2)720°;(3)540°
【分析】(1)连接AD,根据三角形的内角和定理得∠B+∠C=∠BAD+∠CDA,进而将问题转化为求四边形ADEF的内角和,
(2)与(1)方法相同转化为求六边形ABCDEF的内角和,
(3)使用上述方法,转化为求五边形ABCDE的内角和.
【详解】解:(1)如图①,连接AD,
由三角形的内角和定理得,∠B+∠C=∠BAD+∠CDA,
∴∠BAF+∠B+∠C+∠CDE+∠E+∠F=∠BAF+∠BAD+∠CDA+∠D+∠E+∠F
即四边形ADEF的内角和,四边形的内角和为360°,
∴∠BAF+∠B+∠C+∠CDE+∠E+∠F=360°,
(2)如图②,由(1)方法可得:
∠BAH+∠B+∠C+∠D+∠E+∠EFG+∠G+∠H的度数等于六边形ABCDEF的内角和,
∴∠BAH+∠B+∠C+∠D+∠E+∠EFG+∠G+∠H=(6-2)×180°=720°,
(3)如图③,根据(1)的方法得,∠F+∠G=∠GAE+∠FEA,
∠BAG+∠B+∠C+∠D+∠DEF+∠F+∠G的度数等于五边形ABCDE的内角和,
∴∠BAG+∠B+∠C+∠D+∠DEF+∠F+∠G=(5-2)×180°=540°,
【点睛】本题考查三角形的内角和、多边形的内角和的计算方法,适当的转化是解决问题的关键.
多边形的外角
1.在五边形ABCDE中,,,.
(1)如图①,画出五边形ABCDE的所有对角线;
(2)如图②,若比小,求出的度数;
(3)如图③,若CP,DP分别平分与的外角,试求出的度数.
【答案】(1)见解析
(2)
(3)
【分析】(1)根据对角线的定义作出所有对角线即可;
(2)先根据多边形的内角和公式求得内角和,再求出∠C+∠D的度数,最后求得∠D即可;
(3)先根据多边形内角结合外角的定义求得,然后根据角平分线的定义、等量代换、角的和差解答即可.
【详解】(1)解:如图即为所求.
(2)解:五边形ABCDE的内角和为,
∵,,,
∴,
又∵,
∴.
(3)解:五边形ABCDE的内角和为,
∵,,,
∴,
又∵,,
∴,
∵CP平分,DP平分,
∴,,
∴,
又∵,
∴.
【点睛】本题主要考查了多边形的内角和、多边形的外角、对角线以及角平分线的定义等知识点,灵活运用多边形的内角和定理成为解答本题的关键.
2.已如在四边形中,.
(1)如图1,若,则________.
(2)如图2,若、分别平分、,判断与位置关系并证明理由.
(3)如图3,若、分别五等分、(即,),则_______.
【答案】(1)70°;(2)DE∥BF,证明见解析;(3)54°
【分析】(1)根据四边形内角和计算即可;
(2)根据平角的定义和等量代换可得∠MBC+∠CDN=180°,再根据角平分线的定义得到∠CBF+∠CDE=90°,从而推出∠EDB+∠FBD=180°,可得结论;
(3)根据五等分得到∠CDP+∠CBP=36°,连接PC并延长,证明∠DCB=∠DPB+∠CBP+∠CDP,即可计算.
【详解】解:(1)∵∠A=∠C=90°,∠ABC=70°,
∴∠ADC=360°-90°-90°-70°=110°,
∴∠NDC=180°-110°=70°;
(2)DE∥BF,如图,连接BD,
∵∠ABC+∠ADC=180°,
且∠MBC+∠ABC=180°,∠CDN+∠ADC=180°,
∴∠MBC+∠CDN=180°,
∵∠CBF=∠MBC,∠CDE=∠CDN,
∴∠CBF+∠CDE=90°,
∵∠C=90°,
∴∠CBD+∠CDB=90°,
∴∠EDB+∠FBD=∠CBF+∠CDE+∠CBD+∠CDB=180°,
∴DE∥BF;
(3)∵∠MBC+∠CDN=180°,
∴∠CDP+∠CBP=(∠MBC+∠CDN)=36°,
连接PC并延长,
∵∠DCE=∠CDP+∠CPD,∠BCE=∠CPB+∠CBP,
∴∠DCB=∠DCE+∠BCE=∠DPB+∠CBP+∠CDP,
∴∠DPB=90°-36°=54°.
【点睛】本题考查多边形内角和与外角,三角形内角和定理,平行线的判定等知识,解题的关键是学会添加常用辅助线,属于中考常考题型.
3.如图,四边形ABCD中,AD∥BC,∠BDC=∠BCD,DE⊥DC交AB于E.
(1)求证:DE平分∠ADB;
(2)若∠ABD的平分线与CD的延长线交于F,设∠F=α.
①若α=50°,求∠A的值;
②若∠F<,试确定α的取值范围.
【答案】(1)证明见解析;(2)①∠A=100°,理由见解析;②0° <<45°,理由见解析.
【分析】(1)由AD∥BC可得同旁内角,由DE⊥DC可得,再根据已知∠BDC=∠BCD,进而可得,即可证DE平分∠ADB;
(2)①根据AD∥BC,可得∠ADC+∠BCD=180,根据DE平分∠ADB,∠BDC=∠BCD,易得∠ADE=∠EDB,∠EDB+∠BDC=90°,∠DEC+∠ DCE=90°,根据外角和定理等可得∠FBD+∠BDE=90°-∠F=90°-50°=40°,又因为DE平分∠ADB,BF平分∠ABD,从而可得∠ADB+∠ABD=2(∠FBD+∠BDE)=80°,根据三角形内角和定理继而即可取出∠A的值;
②由①知∠FBD+∠BDE= 90°-∠F,根据DE平分∠ADB,BF平分∠ABD,易得∠ADB+∠ABD= 2(∠FBD+∠BDE)= 2(90°-∠F),根据AD // BC的性质可得∠DBC = ∠ADB,∠ABC = 2(90°-∠F),依据∠F<,可得不等式∠F<×2(90°-∠F),解即可得∠F即α的取值范围.
【详解】(1)证明:∵AD∥BC,
∴,
∵DE⊥DC交AB于E,
∴
∴,
∴
∵∠BDC=∠BCD,
∴,
∴DE平分∠ADB;
(2)解:①∵AD∥BC,
∴∠ADC+∠BCD=180,
∵DE平分∠ADB,∠BDC=∠BCD,
∴∠ADE=∠EDB,
∴∠EDB+∠BDC=90°,
∴∠DEC+∠ DCE=90°,
∵∠FBD+∠BDE=90°-∠F=90°-50°=40°,
∵DE平分∠ADB,BF平分∠ABD,
∴∠ADB+∠ABD=2(∠FBD+∠BDE)=80°,
∴∠A = 180°-(∠ADB+∠ABD)=180°- 80°= 100°;
②由①知∠FBD+∠BDE= 90°-∠F,
∵DE平分∠ADB,BF平分∠ABD,
∴∠ADB+∠ABD= 2(∠FBD+∠BDE)= 2(90°-∠F),
又∵在四边形ABCD中,AD // BC,
∴∠DBC = ∠ADB,
∴∠ABC=∠ABD +∠DBC = ∠ABD+∠ADB =2(90°-∠F),
即∠ABC = 2(90°-∠F),
又∵∠F<,
∴∠F<×2(90°-∠F),
∴0° <∠F<45°,
∵∠F=α,
∴0° <α<45°.
【点睛】本题主要考查三角形内角和定理,平行线的性质定理及多边形内角和外角的性质.
4.四边形ABCD中,∠A=145°,∠D=75°.
(1)如图1,若∠B=∠C,试求出∠C的度数;
(2)如图2,若∠ABC的角平分线BE交DC于点E,且BE∥AD,试求出∠C的度数;
(3)①如图3,若∠ABC和∠BCD的角平分线交于点E,试求出∠BEC的度数.
②在①的条件下,若延长BA、CD交于点F(如图4),将原来条件“∠A=145°,∠D=75°”改为“∠F=40°”,其他条件不变,∠BEC的度数会发生变化吗?若不变,请说明理由;若变化,求出∠BEC的度数.
【答案】(1)∠C=70°;(2)∠C=70°;(3)①∠BEC=110°;②不变.∠BEC=110°.
【分析】(1)先根据四边形内角和等于360°求出∠B+∠C的度数,再除以2即可求解;
(2)先根据平行线的性质得到∠ABE的度数,再根据角平分线的定义得到∠ABC的度数,再根据四边形内角和等于360°求出∠BEC的度数;
(3)①先根据四边形内角和等于360°求出∠ABC+∠BCD的度数,再根据角平分线的定义得到∠EBC+∠ECB的度数,再根据三角形内角和等于180°求出∠BEC的度数;
②先根据三角形内角和等于180°求出∠FBC+∠BCF的度数,再根据角平分线的定义得到∠EBC+∠ECB的度数,再根据三角形内角和等于180°求出∠BEC的度数.
【详解】(1)∵四边形ABCD中,∠A=145°,∠D=75°,
∴∠B+∠C=360°-(145°+75°)=140°,
∵∠B=∠C,
∴∠C=70°;
(2)∵BE∥AD,
∴∠ABE=180°-∠A=180°-145°=35°,
∵∠ABC的角平分线BE交DC于点E,
∴∠ABC=70°,
∴∠C=360°-(145°+75°+70°)=70°;
(3)①∵四边形ABCD中,∠A=145°,∠D=75°,
∴∠B+∠C=360°-(145°+75°)=140°,
∵∠ABC和∠BCD的角平分线交于点E,
∴∠EBC+∠ECB=70°,
∴∠BEC=180°-70°=110°;
②不变.
∵∠F=40°,
∴∠FBC+∠BCF=180°-40°=140°,
∵∠ABC和∠BCD的角平分线交于点E,
∴∠EBC+∠ECB=70°,
∴∠BEC=180°-70°=110°.
【点睛】本题考查了多边形内角与外角,解决的关键是综合运用四边形的内角和以及三角形的内角和、熟练运用平行线的性质和角平分线的定义.
5.用地砖铺地,用瓷砖贴墙,都要求砖与砖严丝合缝,不留空隙,把地面或墙面全部覆盖.从数学角度看,这些工作就是用一些不重叠摆放的多边形把平面的一部分完全覆盖,通常把这类问题叫做用多边形覆盖平面(或平面镶嵌)的问题.
(1)如图1是铺在某知名大学数学系大楼入口的彭罗斯地砖,它由如图2和如图3所示的两种不同菱形镶嵌而成.
请观察图形,并填空:______°,______°;
(2)如图4所示的拼合图案是使用全等的正三角形地砖铺成.类似的,单独使用哪几种全等的正多边形能镶嵌成一个平面图案?请证明你的结论;
(3)我们也可以用边长相等的多种正多边形镶嵌平面.如果镶嵌时某个顶点处的正多边形有m个,设这m个正多边形的边数分别为,,…,,请说明m与,,…,应满足什么关系?当时,写出所有满足条件的正多边形的组合.
【答案】(1)72,36
(2)正三角形、正方形、正六边形
(3),当时,满足条件的正多边形的组合为4个正方形;2个正方形,1个正三角形,1个正六边形;2个正三角形、2个正六边形
【分析】本题考查平面镶嵌,涉及等边三角形的性质、正多边形的性质、图形类规律探究,理解平面镶嵌是解答的关键.
(1)从图1中找到图2、图3菱形组成的部分,进而可求解;
(2)只要正多边形的一个内角能整除即可;
(3)先用边数表示出每个正多边形的内角,再根据一个顶点处的m个内角和为求解即可.
【详解】(1)解:由图1可知,,,
∴,,
故答案为:72,36;
(2)解:∵正三角形的每个内角是,能整除,
∴全等的等边三角形能镶嵌成一个平面图案;
设正多边形的边数为n,则正多边形的每个内角为,
∵单独使用全等的正多边形能镶嵌成一个平面图案,
∴能整除,又n为正整数,
∴或4或6,
故单独使用全等的正三角形、正方形、正六边形能镶嵌成一个平面图案;
(3)解:∵正n多边形的每个内角为,
∴正边形内角为,正边形内角为,…,正边形内角为,
由镶嵌条件,得,
则,
∴
当时,,
若这4个正多边形都是正方形时,满足;
若这4个正多边形中,2个正方形,1个正三角形,1个正六边形,满足;
若这4个正多边形中,2个正三角形、2个正六边形时,满足,
综上,当时,满足条件的正多边形的组合为4个正方形;2个正方形,1个正三角形,1个正六边形;2个正三角形、2个正六边形.
凸多边形
凹多边形
凸多边形
凹多边形
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版数学八年级上暑假预习课
第三讲 多边形及其内角和
一、专题导航
知识点梳理
知识点1 多边形
1.定义:在平面内不在同一直线上的一些线段首尾顺次相接所组成的封闭图形叫做多边形.其中,各个角相等、各条边相等的多边形叫做正多边形.
2.相关概念:
边:组成多边形的各条线段叫做多边形的边.
顶点:每相邻两条边的公共端点叫做多边形的顶点.
内角:多边形相邻两边组成的角叫多边形的内角,一个n边形有n个内角.
外角:多边形的边与它的邻边的延长线组成的角叫做多边形的外角.
对角线:连接多边形不相邻的两个顶点的线段,叫做多边形的对角线.
3. 多边形的分类:画出多边形的任何一边所在的直线,如果整个多边形都在这条直线的同一侧,那么这个多边形就是凸多边形,如果整个多边形不在直线的同一侧,这个多边形叫凹多边形.如图:
注意(1)正多边形必须满足两个条件(1)各边相等,各角相等。
(2)过多边形一个顶点有(n-3)条对角线。N边形共有条对角线
(3)过n边形一个顶点把n边形分成(n-2)个三角形。
典例剖析1
例1-1.在如图所示的图形中,属于多边形的有( )
A.2个 B.3个 C.4个 D.5个
例1-2.下列图形是正多边形的是( )
A. B. C. D.
例1-3.若一个多边形的一条对角线将其分成两个四边形,则该多边形的边数是 .
知识点2 多边形的内角和
n边形的内角和定理:n边形的内角和为(n 2) 180°
典例剖析2
例2-1.一个八边形的内角和是( )
A. B. C. D.
例2-2.如果从某个多边形的一个顶点出发的对角线共有6条,那么该多边形的内角和是( )
A. B. C. D.
例2-3.如图,的度数为
例2-4.如图,正六边形,正方形,连接,则图中的度数为 .
知识点3 多边形的外角和
1.n边形的外角和定理:多边形的外角和等于360°(与多边形的形状和边数无关)。
2.平面镶嵌:平面镶嵌是指用形状、大小完全相同的一种或几种平面图形进行拼接,彼此之间不留空隙、不重叠地铺成一片,平面镶嵌又称为平面密铺、“平面图形的镶嵌”。
典例剖析3
例3-1.小聪利用所学的数学知识,给同桌出了这样一道题:假如从点A出发,沿直线走9米后向左转,接着沿直线前进9米后,再向左转,…,如此下去,当他第一次回到点A时,发现自己一共走了72米,则的度数为( )
A. B. C. D.
例3-2.如图,小强站在五边形健身步道的起点P处,沿着P,B,C,D,E,A,P的方向行走,最终回到了P处.在这过程中,小强转过的角度说明了( )
A.五边形的内角和是 B.五边形的外角和是
C.五边形的内角和是 D.五边形的外角和是
例3-3.若一个多边形每一个外角都相等,且一个内角的度数是,则这个多边形是( )
A.正八边形 B.正九边形 C.正十边形 D.正十一边形
例3-4.参加创客兴趣小组的同学,给机器人设定了如图所示的程序,机器人从点O出发,沿直线前进1米后左转,再沿直线前进1米,又向左转……照这样走下去,机器人第一次回到出发地O点时,一共走的路程是( )
A.10米 B.18米 C.20米 D.36米
例3-5 .如图,用一些全等的正五边形按如图方式可以拼成一个环状,使相邻的两个正五边形有公共顶点,所夹的锐角为,图中所示的是前3个正五边形拼接的情况,拼接一圈后,中间会形成一个正多边形,则该正多边形的边数是( )
A.4 B.5 C.6 D.7
变式训练
变式训练1 多边形
1.如图,五边形中,是它的一条对角线.小颎观察图形得出结论“”,她依据的基本事实是 .
2.三角形有几个顶点,几条边,几个内角?四边形有几个顶点,几条边,几个内角?……n边形呢?
3.某数学兴趣小组为了研究多边形中从一个顶点可以作几条对角线,以及该多边形中对角线的总条数与边数的关系,他们决定从以下图形开始寻找规律.
(1)在图5中画出从点出发的所有对角线;
(2)根据探究,整理得到下面表格:
多边形的边数 4 5 6 7 8 ……
从一个顶点出发的对角线的条数 1 2 3 4 5 ……
多边形对角线的总条数 2 5 9 14 20 ……
①表格中______,______;(用含n的代数式表示)
②拓展应用:
若该校要举办足球比赛,总共有个班级参加比赛,规定每个班级都要和其他班级比赛一次,请计算总共要比赛多少场.
变式训练2 多边形的内角和
1.小明在计算一个多边形的内角和时,漏掉了一个内角,结果算得,则这个内角的度数为 .
2.如图,正八边形的对角线,交于点,则的度数是 .
3.小宇阅读了一篇《东方窗棂之美》的文章,文章中有一张如图所示的图片,图中有许多不规则的多边形组成,代表一种自然和谐美.如图是从图图案中提取的由六条线段组成的图形,若,则的度数是 .
变式训练3多边形的外角
1.如果你可以只用一种图形没有重叠、没有间隙地铺满一个平面,那么这种图形就被称为可以“镶嵌”这个平面,完美五边形就是这种图形.如图的五边形是迄今为止人类发现的第15种完美五边形.若度,则 度.
2.如图,七边形中,,的延长线交于点,若,,,的外角和等于,则的度数为 .
3.(1)如图①,都是四边形的外角,试探究,与之间的数量关系;
(2)如图②,都是四边形的外角,试探究与之间的数量关系;
(3)用你发现的结论解决下列问题∶如图③,分别是四边形的外角、的平分线,,求的度数.
4.【教材呈现】根据如图所示的华师版七年级下册教材第77页部分内容,解答下列问题.
如图9.1.9,一个三角形的每一个外角对应一个相邻的内角和两个不相邻的内角.三角形的外角与内角有什么关系呢?在图9.1.10中,显然有(外角)(相邻的内角)那么外角与其他两个不相邻的内角又有什么关系呢?
如图1,请写出与、之间的数量关系,并给出证明.
【拓展延伸】七年级某数学兴趣小组学习了关于三角形外角的性质后,提出问题:四边形的一个外角与它不相邻的三个内角之间具有怎样的数量关系?如图2,已知是四边形的一个外角,直接写出与的数量关系为:______.
【应用提升】如图3,为四边形的一个外角,平分交的角平分线于点F,若,则______°.
5.如图,一个正方形水池的四周恰好被4个正n边形地板铺满,则 .
6.如图所示的地面由正五边形和正n边形两种地砖镶嵌而成,则的度数为 °.
能力提升
多边形
1.同学们,你们会用画多边形的对角线来解决生活中的数学问题吗?
比如,学校举办足球赛,共有5个班级的足球队参加比赛,每个队都要和其他各队比赛一场,根据积分排列名次.问学校一共要安排多少场比赛?
我们画出5个点,每个点各代表一个足球队,两个队之间比赛一场就用一条线段把它们连接起来.由于每个队都要与其他各队比赛一场,这样每个点与另外4个点都会有一条线段连接(如图).
现在我们只要数一数五边形的边数和它的对角线条数就可以了.由图可知,五边形的边数和对角线条数都是5,所以学校一共要安排10场比赛.
同学们,请用类似的方法来解决下面的问题:
姣姣、林林、可可、飞飞、红红和娜娜六人参加一次会议,见面时他们相互握手问好.已知姣姣已握了5次手,林林已握了4次手,可可已握了3次手,飞飞已握了2次手,红红握手1次,请推算出娜娜目前已和哪几个人握了手.
2.连接多边形不相邻的两个顶点的线段,叫做多边形的对角线,如图(1),、是五边形的对角线.思考下列问题:
(1)如图(2),边形中,过顶点可以画 条对角线,它们分别是 ;过顶点可以画 条对角线,过顶点可以画 条对角线.
(2)过顶点的对角线与过顶点的对角线有相同的吗?过顶点的对角线与过顶点的对角线有相同的吗?
(3)在此基础上,你能发现边形的对角线条数的规律吗?
多边形的内角和
1.在中,.点D、E分别在的边上,且均不与的顶点重合,连接,将沿折叠,使点A的对称点始终落在四边形的外部,交边于点F,且点与点C在直线的异侧.
(1)如图①,则_______.
(2)如图②,则_______.
(3)如图③,设图②中的.求的度数;
(4)当的某条边与或垂直时,直接写出的度数.
2.一个多边形纸片剪去一个内角后,得到一个内角和为2340°的新多边形,求原多边形的边数.
3.阅读材料:
如图1,AB、CD交于点O,我们把△AOD和△BOC叫做对顶三角形.
结论:若△AOD和△BOC是对顶三角形,则∠A+∠D=∠B+∠C.
结论应用举例:
如图2:求五角星的五个内角之和,即∠A+∠B+∠ACE+∠ADB+∠E的度数.
解:连接CD,由对顶三角形的性质得:∠B+∠E=∠1+∠2,
在△ACD中,∵∠A+∠ACD+∠ADC=180°,
即∠A+∠3+∠1+∠2+∠4=180°,
∴∠A+∠ACE+∠B+∠E+ADB=180°
即五角星的五个内角之和为180°.
解决问题:
(1)如图①,∠A+∠B+∠C+∠D+∠E+∠F= ;
(2)如图②,∠A+∠B+∠C+∠D+∠E+∠F+∠G= ;
(3)如图③,∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H= ;
(4)如图④,∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠M+∠N= ;
请你从图③或图④中任选一个,写出你的计算过程.
4.(1)如图①,求∠A+∠B+∠C+∠D+∠E+∠F的度数;
(2)如图②,求∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H的度数;
(3)如图③,求∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数.
多边形的外角
1.在五边形ABCDE中,,,.
(1)如图①,画出五边形ABCDE的所有对角线;
(2)如图②,若比小,求出的度数;
(3)如图③,若CP,DP分别平分与的外角,试求出的度数.
2.已如在四边形中,.
(1)如图1,若,则________.
(2)如图2,若、分别平分、,判断与位置关系并证明理由.
(3)如图3,若、分别五等分、(即,),则_______.
3.如图,四边形ABCD中,AD∥BC,∠BDC=∠BCD,DE⊥DC交AB于E.
(1)求证:DE平分∠ADB;
(2)若∠ABD的平分线与CD的延长线交于F,设∠F=α.
①若α=50°,求∠A的值;
②若∠F<,试确定α的取值范围.
4.四边形ABCD中,∠A=145°,∠D=75°.
(1)如图1,若∠B=∠C,试求出∠C的度数;
(2)如图2,若∠ABC的角平分线BE交DC于点E,且BE∥AD,试求出∠C的度数;
(3)①如图3,若∠ABC和∠BCD的角平分线交于点E,试求出∠BEC的度数.
②在①的条件下,若延长BA、CD交于点F(如图4),将原来条件“∠A=145°,∠D=75°”改为“∠F=40°”,其他条件不变,∠BEC的度数会发生变化吗?若不变,请说明理由;若变化,求出∠BEC的度数.
5.用地砖铺地,用瓷砖贴墙,都要求砖与砖严丝合缝,不留空隙,把地面或墙面全部覆盖.从数学角度看,这些工作就是用一些不重叠摆放的多边形把平面的一部分完全覆盖,通常把这类问题叫做用多边形覆盖平面(或平面镶嵌)的问题.
(1)如图1是铺在某知名大学数学系大楼入口的彭罗斯地砖,它由如图2和如图3所示的两种不同菱形镶嵌而成.
请观察图形,并填空:______°,______°;
(2)如图4所示的拼合图案是使用全等的正三角形地砖铺成.类似的,单独使用哪几种全等的正多边形能镶嵌成一个平面图案?请证明你的结论;
(3)我们也可以用边长相等的多种正多边形镶嵌平面.如果镶嵌时某个顶点处的正多边形有m个,设这m个正多边形的边数分别为,,…,,请说明m与,,…,应满足什么关系?当时,写出所有满足条件的正多边形的组合.
人教版数学八年级上暑假预习课
第三讲 多边形及其内角和
一、专题导航
二、知识点梳理
知识点1 多边形
1.定义:在平面内不在同一直线上的一些线段首尾顺次相接所组成的封闭图形叫做多边形.其中,各个角相等、各条边相等的多边形叫做正多边形.
2.相关概念:
边:组成多边形的各条线段叫做多边形的边.
顶点:每相邻两条边的公共端点叫做多边形的顶点.
内角:多边形相邻两边组成的角叫多边形的内角,一个n边形有n个内角.
外角:多边形的边与它的邻边的延长线组成的角叫做多边形的外角.
对角线:连接多边形不相邻的两个顶点的线段,叫做多边形的对角线.
3. 多边形的分类:画出多边形的任何一边所在的直线,如果整个多边形都在这条直线的同一侧,那么这个多边形就是凸多边形,如果整个多边形不在直线的同一侧,这个多边形叫凹多边形.如图:
注意(1)正多边形必须满足两个条件(1)各边相等,各角相等。
(2)过多边形一个顶点有(n-3)条对角线。N边形共有条对角线
(3)过n边形一个顶点把n边形分成(n-2)个三角形。
典例剖析1
例1-1.在如图所示的图形中,属于多边形的有( )
A.2个 B.3个 C.4个 D.5个
【答案】C
【分析】本题考查多边形定义,根据多边形定义,逐个验证即可得到答案.
【详解】解:所示的图形中,第一个是三角形、第二个是四边形、第三个是圆、第四个是正六边形、第五个是正方体,
是多边形的有第一个、第二个、第四个,共有3个,
故选:C.
例1-2.下列图形是正多边形的是( )
A. B. C. D.
【答案】C
【分析】本题主要考查了正多边形,根据正多边形的定义;各个角都相等,各条边都相等的多边形叫做正多边形可得答案.
【详解】解:A.是等腰三角形,不是正多边形,故选项A不符合题意;
B.是圆角矩形,不是正多边形,故选项B不符合题意;
C.是正五边形,符合题意;
D.是一般六边形,不是正多边形,故选项D不符合题意;
故选:C.
例1-3.若一个多边形的一条对角线将其分成两个四边形,则该多边形的边数是 .
【答案】六/
【分析】本题考查了多边形的对角线,根据一个多边形被一条对角线分成两个四边形,可得多边形的边数,可得答案.
【详解】解:两个四边形有一条公共边,得多边形边的数目是,
故答案为:六.
知识点2 多边形的内角和
n边形的内角和定理:n边形的内角和为(n 2) 180°
典例剖析2
例2-1.一个八边形的内角和是( )
A. B. C. D.
【答案】A
【分析】本题考查了多边形的内角和,熟记内角和公式是解题的关键.根据多边形的内角和公式,列式进行计算即可得解.
【详解】解:.
故选: A
例2-2.如果从某个多边形的一个顶点出发的对角线共有6条,那么该多边形的内角和是( )
A. B. C. D.
【答案】D
【分析】本题考查了多边形的内角和公式,多边形的对角线的公式,求出多边形的边数是解题的关键.
根据从n边形的一个顶点可以作对角线的条数为条,求出边数,然后根据多边形的内角和公式,列式进行计算即可得解.
【详解】多边形从一个顶点出发可引出6条对角线,
,
解得:,
内角和,
故选:D.
例2-3.如图,的度数为
【答案】
【分析】此题主要考查了复杂图形角的和.熟练掌握三角形外角性质,四边形内角和定理,是解决问题的关键.
根据三角形外角的性质,,四边形内角和等于,可得的度数.
【详解】如图,
,
,
,
故答案为:.
例2-4.如图,正六边形,正方形,连接,则图中的度数为 .
【答案】/15度
【分析】本题考查了正多边形的内角,等腰三角形的判定即性质,熟悉掌握正多边形的内角运算方法是解题的关键.
利用正多边形的内角度数求法运算出正六边形和正方形的内角度数,即可得到的度数,再利用等腰三角形的性质运算求解即可.
【详解】解:∵正六边形的内角度数为:,正方形的内角度数为:,
∴,,
∴,
∵,
∴,
故答案为:.
知识点3 多边形的外角和
1.n边形的外角和定理:多边形的外角和等于360°(与多边形的形状和边数无关)。
2.平面镶嵌:平面镶嵌是指用形状、大小完全相同的一种或几种平面图形进行拼接,彼此之间不留空隙、不重叠地铺成一片,平面镶嵌又称为平面密铺、“平面图形的镶嵌”。
典例剖析3
例3-1.小聪利用所学的数学知识,给同桌出了这样一道题:假如从点A出发,沿直线走9米后向左转,接着沿直线前进9米后,再向左转,…,如此下去,当他第一次回到点A时,发现自己一共走了72米,则的度数为( )
A. B. C. D.
【答案】D
【分析】本题考查了多边形的内角与外角,解决本题的关键是明确第一次回到出发点A时,所经过的路线正好构成一个正多边形.第一次回到出发点A时,所经过的路线正好构成一个正多边形,用,求得边数,再根据多边形的外角和为,即可求解.
【详解】解:∵第一次回到出发点A时,所经过的路线正好构成一个正多边形,
∴正多边形的边数为:,
根据多边形的外角和为,
∴则他每次转动θ的角度为:,
故选:D.
例3-2.如图,小强站在五边形健身步道的起点P处,沿着P,B,C,D,E,A,P的方向行走,最终回到了P处.在这过程中,小强转过的角度说明了( )
A.五边形的内角和是 B.五边形的外角和是
C.五边形的内角和是 D.五边形的外角和是
【答案】B
【分析】本题主要考查多边形的内角和外角.根据题意可知小强转过的角度之和正好是五边形的外角和,再根据多边形的外角和性质即可得出答案.
【详解】解:小强转过的角度之和正好是五边形的外角和,
小强转过的角度之和为.
故选:B.
例3-3.若一个多边形每一个外角都相等,且一个内角的度数是,则这个多边形是( )
A.正八边形 B.正九边形 C.正十边形 D.正十一边形
【答案】B
【分析】本题考查了正多边形的外角与外角和的关系,需要熟练掌握并灵活运用.
先根据平角的定义求出每一个外角的度数,再根据边数外角度数计算即可.
【详解】解:,
,
这个多边形是正九边形.
故选:B.
例3-4.参加创客兴趣小组的同学,给机器人设定了如图所示的程序,机器人从点O出发,沿直线前进1米后左转,再沿直线前进1米,又向左转……照这样走下去,机器人第一次回到出发地O点时,一共走的路程是( )
A.10米 B.18米 C.20米 D.36米
【答案】C
【分析】本题考查了多边形的外角和定理的应用.由题意可知小华所走的路线为一个正多边形,根据多边形的外角和即可求出答案.
【详解】解:∵,
∴他需要走20次才会回到原来的起点,
即一共走了(米).
故选:C
例3-5 .如图,用一些全等的正五边形按如图方式可以拼成一个环状,使相邻的两个正五边形有公共顶点,所夹的锐角为,图中所示的是前3个正五边形拼接的情况,拼接一圈后,中间会形成一个正多边形,则该正多边形的边数是( )
A.4 B.5 C.6 D.7
【答案】C
【分析】本题考查了正多边形、多边形的内角与外角等知识;由完全拼成一个圆环需要的正五边形为个,则围成的多边形为正边形,利用正五边形的内角与夹角计算出正边的每个内角的度数,然后根据内角和定理得到解方程求解即可.
【详解】∵正五边形的每个内角为,
∴组成的正多边形的每个内角为,
∵n个全等的正五边形拼接可以拼成一个环状,中间会形成一个正多边形,
∴形成的正多边形为正n边形,则,
解得:.
故选C.
三、变式训练
变式训练1 多边形
1.如图,五边形中,是它的一条对角线.小颎观察图形得出结论“”,她依据的基本事实是 .
【答案】两点之间线段最短
【分析】本题考查线段的性质,根据两点之间,线段最短,进行作答即可.
【详解】解:依据的基本事实是:两点之间线段最短;
故答案为:两点之间线段最短.
2.三角形有几个顶点,几条边,几个内角?四边形有几个顶点,几条边,几个内角?……n边形呢?
【答案】见解析
【分析】根据图形的特征作答即可.
【详解】解:如图所示,三角形有3个顶点,3条边,3个内角;
四边形有4个顶点,4条边,4个内角;
五边形有5个顶点,5条边,5个内角;
……
可发现,多边形的顶点个数和内角个数与边数相同;
n边形有n个顶点,n条边,n个内角.
【点睛】本题考查了多边形的有关概念,解题关键是准确识别多边形,明确多边形的顶点和内角概念.
3.某数学兴趣小组为了研究多边形中从一个顶点可以作几条对角线,以及该多边形中对角线的总条数与边数的关系,他们决定从以下图形开始寻找规律.
(1)在图5中画出从点出发的所有对角线;
(2)根据探究,整理得到下面表格:
多边形的边数 4 5 6 7 8 ……
从一个顶点出发的对角线的条数 1 2 3 4 5 ……
多边形对角线的总条数 2 5 9 14 20 ……
①表格中______,______;(用含n的代数式表示)
②拓展应用:
若该校要举办足球比赛,总共有个班级参加比赛,规定每个班级都要和其他班级比赛一次,请计算总共要比赛多少场.
【答案】(1)见解析
(2)①,;②场
【分析】本题考查了多边形的对角线,根据表格信息寻求规律是解题的关键.
(1)连接作图即可;
(2)①根据所给数据规律解答即可;
②根据每班都需要和对手比赛一次,且一次比赛能满足2个班级的比赛需求列式运算即可.
【详解】(1)如图所示,即为所求;
(2)解:①,;
②(场),
答:共需要比赛场.
变式训练2 多边形的内角和
1.小明在计算一个多边形的内角和时,漏掉了一个内角,结果算得,则这个内角的度数为 .
【答案】/100度
【分析】设这个多边形的边数是n,根据漏掉的那个内角的范围介于可得关于n的不等式组,求出n的范围结合n为正整数即得答案.
【详解】解析:设这个多边形的边数是n,
依题意,得,
解得.
又n为正整数,
∴.
∴这个内角的度数为.
故答案为:.
【点睛】本题考查了多边形的内角和,正确理解题意、求出n的范围是关键.
2.如图,正八边形的对角线,交于点,则的度数是 .
【答案】
【分析】本题主要考查多边形内角和外角,先求出,再根据正八边形的性质求出和,最后根据三角形的内角和即可求得.
【详解】解:∵八边形为正八边形,
∵,
∵正八边形的对角线,
∴,
又,
∴,
∴.
故答案为:67.5.
3.小宇阅读了一篇《东方窗棂之美》的文章,文章中有一张如图所示的图片,图中有许多不规则的多边形组成,代表一种自然和谐美.如图是从图图案中提取的由六条线段组成的图形,若,则的度数是 .
【答案】/300度
【分析】本题考查了多边形的外角,根据外角和为即可求解.
【详解】多边形的外角和等于
故答案为:.
变式训练3多边形的外角
1.如果你可以只用一种图形没有重叠、没有间隙地铺满一个平面,那么这种图形就被称为可以“镶嵌”这个平面,完美五边形就是这种图形.如图的五边形是迄今为止人类发现的第15种完美五边形.若度,则 度.
【答案】285
【分析】本题考查多边形的外角和,根据多边形的外角和为360度,进行求解即可.
【详解】解:由题意,得:,
∵度,
∴;
故答案为:285
2.如图,七边形中,,的延长线交于点,若,,,的外角和等于,则的度数为 .
【答案】/40度
【分析】本题考查了多边形内角和问题,熟练掌握多边形的内角和等于是解题的关键.根据题意计算,,,的度数之和,再计算五边形的内角和,即可求解.
【详解】解:,,,的外角和等于,
,
五边形的内角和为,
.
故答案为:.
3.(1)如图①,都是四边形的外角,试探究,与之间的数量关系;
(2)如图②,都是四边形的外角,试探究与之间的数量关系;
(3)用你发现的结论解决下列问题∶如图③,分别是四边形的外角、的平分线,,求的度数.
【答案】(1);(2);(3)
【分析】本题考查了多边形的内角和公式,平角的定义,角平分线的定义,整体思想的利用是解题的关键.
(1)根据四边形的内角和等于表示出,再根据平角的定义用表示出,即可得解;
(2)从外角的定义考虑解答;
(3)根据(1)、(2)的结论求出,再根据角平分线的定义求出,然后利用三角形的内角和定理列式进行计算即可得解.
【详解】(1)∵,
,
,,
,
;
(2)∵,
,
,,
,
,
(3),
根据(1)和(2)的结论有:,
分别是的平分线,
,,
,
.
4.【教材呈现】根据如图所示的华师版七年级下册教材第77页部分内容,解答下列问题.
如图9.1.9,一个三角形的每一个外角对应一个相邻的内角和两个不相邻的内角.三角形的外角与内角有什么关系呢?在图9.1.10中,显然有(外角)(相邻的内角)那么外角与其他两个不相邻的内角又有什么关系呢?
如图1,请写出与、之间的数量关系,并给出证明.
【拓展延伸】七年级某数学兴趣小组学习了关于三角形外角的性质后,提出问题:四边形的一个外角与它不相邻的三个内角之间具有怎样的数量关系?如图2,已知是四边形的一个外角,直接写出与的数量关系为:______.
【应用提升】如图3,为四边形的一个外角,平分交的角平分线于点F,若,则______°.
【答案】(教材呈现),证明见解析;(拓展延伸);(应用提升)
【分析】本题考查三角形与四边形的内角和,三角形的外角,角平分线的定义.
(教材呈现)根据三角形的内角和定理与邻补角互补即可解答;
(拓展延伸)根据四边形的内角和定理与邻补角互补即可解答;
(应用提升)由(教材呈现)可知,由角平分线的定义可得,,又由(拓展延伸)可知,从而,化简即可解答.
【详解】解:(教材呈现)
,
证明:∵,,
∴;
(拓展延伸)
∵,,
∴,
∵,
∴,
故答案为:;
(应用提升)
由(教材呈现)可知
∵平分,平分
∴,,
由(拓展延伸)可知,
∴,
∴,
∴.
故答案为:
5.如图,一个正方形水池的四周恰好被4个正n边形地板铺满,则 .
【答案】8
【分析】本题考查学生对平面镶嵌知识的掌握情况,体现了学数学用数学的思想,同时考查了多边形的内角和公式.根据平面镶嵌的条件,先求出正n边形的一个内角的度数,再根据内角和公式求出n的值.
【详解】解:正n边形的一个内角,
则,
解得,
故答案为:8.
6.如图所示的地面由正五边形和正n边形两种地砖镶嵌而成,则的度数为 °.
【答案】
【分析】本题考查了正多边形的内角和公式,掌握正多边形的概念,数形结合是解题的关键.先计算出正五边形的内角,再根据平面镶嵌的条件计算求解.
【详解】正五边形的内角和为,
每个内角为,
∴,
故答案为:.
四、能力提升
多边形
1.同学们,你们会用画多边形的对角线来解决生活中的数学问题吗?
比如,学校举办足球赛,共有5个班级的足球队参加比赛,每个队都要和其他各队比赛一场,根据积分排列名次.问学校一共要安排多少场比赛?
我们画出5个点,每个点各代表一个足球队,两个队之间比赛一场就用一条线段把它们连接起来.由于每个队都要与其他各队比赛一场,这样每个点与另外4个点都会有一条线段连接(如图).
现在我们只要数一数五边形的边数和它的对角线条数就可以了.由图可知,五边形的边数和对角线条数都是5,所以学校一共要安排10场比赛.
同学们,请用类似的方法来解决下面的问题:
姣姣、林林、可可、飞飞、红红和娜娜六人参加一次会议,见面时他们相互握手问好.已知姣姣已握了5次手,林林已握了4次手,可可已握了3次手,飞飞已握了2次手,红红握手1次,请推算出娜娜目前已和哪几个人握了手.
【答案】姣姣、林林和可可三人已与娜娜握过手
【分析】本题考查了多边形的对角线的问题,解题的关键是将实际问题与数学问题有机的结合起来.
先画出6个点,A、、、、、各个点依次代表姣姣、林林、可可、飞飞、红红和娜娜,凡是两人之间握过手,就把代表他们的这两点用1条线段连接起来即可得到答案.
【详解】解:先画出6个点,A、、、、、各个点依次代表姣姣、林林、可可、飞飞、红红和娜娜,凡是两人之间握过手,就把代表他们的这两点用1条线段连接起来(如图所示).
先看姣姣(A)和红红(E).姣姣已握手5次,说明姣姣与另外5人都握了手,因此代表姣姣的A点与、、、、这5点都有一条线段连接;红红握手1次,他只能是与姣姣握的手了,所以点只能与A点之间有线段连接,与其它各点再也不能有线段连接了.
其次分析林林(B).林林已握手4次,由于他没有可能与红红握过手,所以只能是与剩下的四个人姣姣、可可、飞飞和娜娜握过手了,因此,点与A、、、四点之间有线段连接.
再看飞飞(D).飞飞已握手2次,而代表飞飞的点已与A、两点有线段连接了,所以点与其它的点不能再有线段连接了.
最后考察可可(C).可可与3人握了手,但已不能是与飞飞和红红握的手了,所以代表可可得点只能与A、、三点有线段连接.
现在观察图形,与代表娜娜的点连接的线段有3条、和,这说明姣姣、林林和可可三人已与娜娜握过手.
2.连接多边形不相邻的两个顶点的线段,叫做多边形的对角线,如图(1),、是五边形的对角线.思考下列问题:
(1)如图(2),边形中,过顶点可以画 条对角线,它们分别是 ;过顶点可以画 条对角线,过顶点可以画 条对角线.
(2)过顶点的对角线与过顶点的对角线有相同的吗?过顶点的对角线与过顶点的对角线有相同的吗?
(3)在此基础上,你能发现边形的对角线条数的规律吗?
【答案】(1),,,
(2)过点的和过点的没有重复的,但和过点的有重复的和重复)
(3)边形的对角线条数的为
【分析】此题考查了多边形的对角线的知识.
(1)过点和任意不相邻的两点连接可得出到一条对角线;同理可得过点、的情况.
(2)过点的和过点的没有重复的,但和过点的有重复的和重复);
(3)过每一点有条对角线,除去重复的即可得出总对角线的条数.
【详解】(1)解:过顶点可以画条对角线,它们分别是;
过顶点可以画条对角线,
过顶点可以画条对角线;
故答案为:,,,;
(2)解:过点的和过点的没有重复的,但和过点的有重复的和重复);
(3)解:边形的一个顶点不能与它本身及左右两个邻点相连成对角线,故可连出条,
共有个顶点,应为条,这样算出的数,正好多出了一倍,所以再除以2.
即边形的对角线条数的为.
多边形的内角和
1.在中,.点D、E分别在的边上,且均不与的顶点重合,连接,将沿折叠,使点A的对称点始终落在四边形的外部,交边于点F,且点与点C在直线的异侧.
(1)如图①,则_______.
(2)如图②,则_______.
(3)如图③,设图②中的.求的度数;
(4)当的某条边与或垂直时,直接写出的度数.
【答案】(1)48
(2)222
(3)
(4)或
【分析】本题考查的是三角形内角和定理,四边形的内角和定理,平行的性质和折叠的性质,熟悉相关性质并能熟练应用是解题的关键.
(1)根据三角形内角和定理可得的度数;
(2)根据四边形内角和定理可得的度数;
(3)由(2)的结论可得,由折叠可得,由三角形内角和定理可得,两式相减,可得答案;
(4)分两种情况:或或时,分别求解即可.
【详解】(1)解:,
故答案为:48;
(2)解:,
,
故答案为:222;
(3)解:由(2)知,
,
由折叠知,
,
,
得:;
(4)解:如图,当时,
,
,
,
由(3)知,
,
由折叠知,
;
如图,当时,
;
如图,当时,点与点C在直线的同侧,不合题意;
综上可知,的度数为或.
2.一个多边形纸片剪去一个内角后,得到一个内角和为2340°的新多边形,求原多边形的边数.
【答案】14或15或16.
【分析】根据多边形内角和公式,可得新多边形的边数;由剪去一个内角可分为三种情况:①截线都不经过顶点;②截线一端经过顶点;③截线两端都经过顶点;进行分类讨论,即可得到原来的边数.
【详解】解:根据题意,得
,
解得:,
新多边形的边数为15;
①如图,当截线都不经过顶点时,新多边形的边数比原来的多边形的边数多1,则
原多边形的边数为:;
②如图,当截线一端经过顶点时,新多边形的边数等于原来的多边形的边数,则
原多边形的边数为:15;
③如图,当截线两端都经过顶点时,新多边形的边数比原来的多边形的边数少1,则
原多边形的边数为:;
综合上述,原多边形的边数为:14或15或16.
【点睛】此题主要考查了多边形的内角和定理的应用,要熟练掌握,解答此题的关键是先求出新多边形的边数,然后根据剪去一个内角的方法进行分类讨论,从而得到答案.
3.阅读材料:
如图1,AB、CD交于点O,我们把△AOD和△BOC叫做对顶三角形.
结论:若△AOD和△BOC是对顶三角形,则∠A+∠D=∠B+∠C.
结论应用举例:
如图2:求五角星的五个内角之和,即∠A+∠B+∠ACE+∠ADB+∠E的度数.
解:连接CD,由对顶三角形的性质得:∠B+∠E=∠1+∠2,
在△ACD中,∵∠A+∠ACD+∠ADC=180°,
即∠A+∠3+∠1+∠2+∠4=180°,
∴∠A+∠ACE+∠B+∠E+ADB=180°
即五角星的五个内角之和为180°.
解决问题:
(1)如图①,∠A+∠B+∠C+∠D+∠E+∠F= ;
(2)如图②,∠A+∠B+∠C+∠D+∠E+∠F+∠G= ;
(3)如图③,∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H= ;
(4)如图④,∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠M+∠N= ;
请你从图③或图④中任选一个,写出你的计算过程.
【答案】(1)360°;(2)540°;(3)720°;(4)1080°;过程见解析
【分析】(1)连接CD,由对顶角三角形可得∠A+∠B=∠BDC+∠ACD,再由四边形的内角和定理得出结论;
(2)连接ED,由对顶角三角形可得∠A+∠B=∠BED+∠ADE,再由五边形的内角和定理得出结论;
(3)连接BH、DE,由对顶角三角形可知∠EBH+∠BHD=∠HDE+∠BED,再根据五边形的内角和定理得出结论;
(4)连接ND、NE,由对顶角三角形可知∠1+∠2=∠NGH+∠EHG,再由六边形的内角和定理得出结论.
【详解】解:(1)连接CD,由对顶角三角形可得∠A+∠B=∠BDC+∠ACD,则∠A+∠B+∠C+∠D+∠E+∠F=360°;
(2)连接ED,由对顶角三角形可得∠A+∠B=∠BED+∠ADE,则∠A+∠B+∠C+∠D+∠E+∠F+∠G=540°;
(3)连接BH、DE,
∵由对顶角三角形可知∠EBH+∠BHD=∠HDE+∠BED,
∴∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H=五边形CDEFG的内角和+△ABH的内角和=540°+180°=720°;
(4)连接ND、NE,
∵由对顶角三角形可知∠1+∠2=∠NGH+∠EHG,
∴∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠M+∠N=六边形BCFGHM的内角和+△AND的内角和+△NDE的内角和=(6-2)×180°+360°=1080°.
故答案为:360°;540°;720°;1080°.
【点睛】本题考查的是三角形内角和定理,根据题意作出辅助线,利用△AOD和△BOC叫做对顶三角形的性质及多边形的内角和定理解答是解答此题的关键.
4.(1)如图①,求∠A+∠B+∠C+∠D+∠E+∠F的度数;
(2)如图②,求∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H的度数;
(3)如图③,求∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数.
【答案】(1)360°;(2)720°;(3)540°
【分析】(1)连接AD,根据三角形的内角和定理得∠B+∠C=∠BAD+∠CDA,进而将问题转化为求四边形ADEF的内角和,
(2)与(1)方法相同转化为求六边形ABCDEF的内角和,
(3)使用上述方法,转化为求五边形ABCDE的内角和.
【详解】解:(1)如图①,连接AD,
由三角形的内角和定理得,∠B+∠C=∠BAD+∠CDA,
∴∠BAF+∠B+∠C+∠CDE+∠E+∠F=∠BAF+∠BAD+∠CDA+∠D+∠E+∠F
即四边形ADEF的内角和,四边形的内角和为360°,
∴∠BAF+∠B+∠C+∠CDE+∠E+∠F=360°,
(2)如图②,由(1)方法可得:
∠BAH+∠B+∠C+∠D+∠E+∠EFG+∠G+∠H的度数等于六边形ABCDEF的内角和,
∴∠BAH+∠B+∠C+∠D+∠E+∠EFG+∠G+∠H=(6-2)×180°=720°,
(3)如图③,根据(1)的方法得,∠F+∠G=∠GAE+∠FEA,
∠BAG+∠B+∠C+∠D+∠DEF+∠F+∠G的度数等于五边形ABCDE的内角和,
∴∠BAG+∠B+∠C+∠D+∠DEF+∠F+∠G=(5-2)×180°=540°,
【点睛】本题考查三角形的内角和、多边形的内角和的计算方法,适当的转化是解决问题的关键.
多边形的外角
1.在五边形ABCDE中,,,.
(1)如图①,画出五边形ABCDE的所有对角线;
(2)如图②,若比小,求出的度数;
(3)如图③,若CP,DP分别平分与的外角,试求出的度数.
【答案】(1)见解析
(2)
(3)
【分析】(1)根据对角线的定义作出所有对角线即可;
(2)先根据多边形的内角和公式求得内角和,再求出∠C+∠D的度数,最后求得∠D即可;
(3)先根据多边形内角结合外角的定义求得,然后根据角平分线的定义、等量代换、角的和差解答即可.
【详解】(1)解:如图即为所求.
(2)解:五边形ABCDE的内角和为,
∵,,,
∴,
又∵,
∴.
(3)解:五边形ABCDE的内角和为,
∵,,,
∴,
又∵,,
∴,
∵CP平分,DP平分,
∴,,
∴,
又∵,
∴.
【点睛】本题主要考查了多边形的内角和、多边形的外角、对角线以及角平分线的定义等知识点,灵活运用多边形的内角和定理成为解答本题的关键.
2.已如在四边形中,.
(1)如图1,若,则________.
(2)如图2,若、分别平分、,判断与位置关系并证明理由.
(3)如图3,若、分别五等分、(即,),则_______.
【答案】(1)70°;(2)DE∥BF,证明见解析;(3)54°
【分析】(1)根据四边形内角和计算即可;
(2)根据平角的定义和等量代换可得∠MBC+∠CDN=180°,再根据角平分线的定义得到∠CBF+∠CDE=90°,从而推出∠EDB+∠FBD=180°,可得结论;
(3)根据五等分得到∠CDP+∠CBP=36°,连接PC并延长,证明∠DCB=∠DPB+∠CBP+∠CDP,即可计算.
【详解】解:(1)∵∠A=∠C=90°,∠ABC=70°,
∴∠ADC=360°-90°-90°-70°=110°,
∴∠NDC=180°-110°=70°;
(2)DE∥BF,如图,连接BD,
∵∠ABC+∠ADC=180°,
且∠MBC+∠ABC=180°,∠CDN+∠ADC=180°,
∴∠MBC+∠CDN=180°,
∵∠CBF=∠MBC,∠CDE=∠CDN,
∴∠CBF+∠CDE=90°,
∵∠C=90°,
∴∠CBD+∠CDB=90°,
∴∠EDB+∠FBD=∠CBF+∠CDE+∠CBD+∠CDB=180°,
∴DE∥BF;
(3)∵∠MBC+∠CDN=180°,
∴∠CDP+∠CBP=(∠MBC+∠CDN)=36°,
连接PC并延长,
∵∠DCE=∠CDP+∠CPD,∠BCE=∠CPB+∠CBP,
∴∠DCB=∠DCE+∠BCE=∠DPB+∠CBP+∠CDP,
∴∠DPB=90°-36°=54°.
【点睛】本题考查多边形内角和与外角,三角形内角和定理,平行线的判定等知识,解题的关键是学会添加常用辅助线,属于中考常考题型.
3.如图,四边形ABCD中,AD∥BC,∠BDC=∠BCD,DE⊥DC交AB于E.
(1)求证:DE平分∠ADB;
(2)若∠ABD的平分线与CD的延长线交于F,设∠F=α.
①若α=50°,求∠A的值;
②若∠F<,试确定α的取值范围.
【答案】(1)证明见解析;(2)①∠A=100°,理由见解析;②0° <<45°,理由见解析.
【分析】(1)由AD∥BC可得同旁内角,由DE⊥DC可得,再根据已知∠BDC=∠BCD,进而可得,即可证DE平分∠ADB;
(2)①根据AD∥BC,可得∠ADC+∠BCD=180,根据DE平分∠ADB,∠BDC=∠BCD,易得∠ADE=∠EDB,∠EDB+∠BDC=90°,∠DEC+∠ DCE=90°,根据外角和定理等可得∠FBD+∠BDE=90°-∠F=90°-50°=40°,又因为DE平分∠ADB,BF平分∠ABD,从而可得∠ADB+∠ABD=2(∠FBD+∠BDE)=80°,根据三角形内角和定理继而即可取出∠A的值;
②由①知∠FBD+∠BDE= 90°-∠F,根据DE平分∠ADB,BF平分∠ABD,易得∠ADB+∠ABD= 2(∠FBD+∠BDE)= 2(90°-∠F),根据AD // BC的性质可得∠DBC = ∠ADB,∠ABC = 2(90°-∠F),依据∠F<,可得不等式∠F<×2(90°-∠F),解即可得∠F即α的取值范围.
【详解】(1)证明:∵AD∥BC,
∴,
∵DE⊥DC交AB于E,
∴
∴,
∴
∵∠BDC=∠BCD,
∴,
∴DE平分∠ADB;
(2)解:①∵AD∥BC,
∴∠ADC+∠BCD=180,
∵DE平分∠ADB,∠BDC=∠BCD,
∴∠ADE=∠EDB,
∴∠EDB+∠BDC=90°,
∴∠DEC+∠ DCE=90°,
∵∠FBD+∠BDE=90°-∠F=90°-50°=40°,
∵DE平分∠ADB,BF平分∠ABD,
∴∠ADB+∠ABD=2(∠FBD+∠BDE)=80°,
∴∠A = 180°-(∠ADB+∠ABD)=180°- 80°= 100°;
②由①知∠FBD+∠BDE= 90°-∠F,
∵DE平分∠ADB,BF平分∠ABD,
∴∠ADB+∠ABD= 2(∠FBD+∠BDE)= 2(90°-∠F),
又∵在四边形ABCD中,AD // BC,
∴∠DBC = ∠ADB,
∴∠ABC=∠ABD +∠DBC = ∠ABD+∠ADB =2(90°-∠F),
即∠ABC = 2(90°-∠F),
又∵∠F<,
∴∠F<×2(90°-∠F),
∴0° <∠F<45°,
∵∠F=α,
∴0° <α<45°.
【点睛】本题主要考查三角形内角和定理,平行线的性质定理及多边形内角和外角的性质.
4.四边形ABCD中,∠A=145°,∠D=75°.
(1)如图1,若∠B=∠C,试求出∠C的度数;
(2)如图2,若∠ABC的角平分线BE交DC于点E,且BE∥AD,试求出∠C的度数;
(3)①如图3,若∠ABC和∠BCD的角平分线交于点E,试求出∠BEC的度数.
②在①的条件下,若延长BA、CD交于点F(如图4),将原来条件“∠A=145°,∠D=75°”改为“∠F=40°”,其他条件不变,∠BEC的度数会发生变化吗?若不变,请说明理由;若变化,求出∠BEC的度数.
【答案】(1)∠C=70°;(2)∠C=70°;(3)①∠BEC=110°;②不变.∠BEC=110°.
【分析】(1)先根据四边形内角和等于360°求出∠B+∠C的度数,再除以2即可求解;
(2)先根据平行线的性质得到∠ABE的度数,再根据角平分线的定义得到∠ABC的度数,再根据四边形内角和等于360°求出∠BEC的度数;
(3)①先根据四边形内角和等于360°求出∠ABC+∠BCD的度数,再根据角平分线的定义得到∠EBC+∠ECB的度数,再根据三角形内角和等于180°求出∠BEC的度数;
②先根据三角形内角和等于180°求出∠FBC+∠BCF的度数,再根据角平分线的定义得到∠EBC+∠ECB的度数,再根据三角形内角和等于180°求出∠BEC的度数.
【详解】(1)∵四边形ABCD中,∠A=145°,∠D=75°,
∴∠B+∠C=360°-(145°+75°)=140°,
∵∠B=∠C,
∴∠C=70°;
(2)∵BE∥AD,
∴∠ABE=180°-∠A=180°-145°=35°,
∵∠ABC的角平分线BE交DC于点E,
∴∠ABC=70°,
∴∠C=360°-(145°+75°+70°)=70°;
(3)①∵四边形ABCD中,∠A=145°,∠D=75°,
∴∠B+∠C=360°-(145°+75°)=140°,
∵∠ABC和∠BCD的角平分线交于点E,
∴∠EBC+∠ECB=70°,
∴∠BEC=180°-70°=110°;
②不变.
∵∠F=40°,
∴∠FBC+∠BCF=180°-40°=140°,
∵∠ABC和∠BCD的角平分线交于点E,
∴∠EBC+∠ECB=70°,
∴∠BEC=180°-70°=110°.
【点睛】本题考查了多边形内角与外角,解决的关键是综合运用四边形的内角和以及三角形的内角和、熟练运用平行线的性质和角平分线的定义.
5.用地砖铺地,用瓷砖贴墙,都要求砖与砖严丝合缝,不留空隙,把地面或墙面全部覆盖.从数学角度看,这些工作就是用一些不重叠摆放的多边形把平面的一部分完全覆盖,通常把这类问题叫做用多边形覆盖平面(或平面镶嵌)的问题.
(1)如图1是铺在某知名大学数学系大楼入口的彭罗斯地砖,它由如图2和如图3所示的两种不同菱形镶嵌而成.
请观察图形,并填空:______°,______°;
(2)如图4所示的拼合图案是使用全等的正三角形地砖铺成.类似的,单独使用哪几种全等的正多边形能镶嵌成一个平面图案?请证明你的结论;
(3)我们也可以用边长相等的多种正多边形镶嵌平面.如果镶嵌时某个顶点处的正多边形有m个,设这m个正多边形的边数分别为,,…,,请说明m与,,…,应满足什么关系?当时,写出所有满足条件的正多边形的组合.
【答案】(1)72,36
(2)正三角形、正方形、正六边形
(3),当时,满足条件的正多边形的组合为4个正方形;2个正方形,1个正三角形,1个正六边形;2个正三角形、2个正六边形
【分析】本题考查平面镶嵌,涉及等边三角形的性质、正多边形的性质、图形类规律探究,理解平面镶嵌是解答的关键.
(1)从图1中找到图2、图3菱形组成的部分,进而可求解;
(2)只要正多边形的一个内角能整除即可;
(3)先用边数表示出每个正多边形的内角,再根据一个顶点处的m个内角和为求解即可.
【详解】(1)解:由图1可知,,,
∴,,
故答案为:72,36;
(2)解:∵正三角形的每个内角是,能整除,
∴全等的等边三角形能镶嵌成一个平面图案;
设正多边形的边数为n,则正多边形的每个内角为,
∵单独使用全等的正多边形能镶嵌成一个平面图案,
∴能整除,又n为正整数,
∴或4或6,
故单独使用全等的正三角形、正方形、正六边形能镶嵌成一个平面图案;
(3)解:∵正n多边形的每个内角为,
∴正边形内角为,正边形内角为,…,正边形内角为,
由镶嵌条件,得,
则,
∴
当时,,
若这4个正多边形都是正方形时,满足;
若这4个正多边形中,2个正方形,1个正三角形,1个正六边形,满足;
若这4个正多边形中,2个正三角形、2个正六边形时,满足,
综上,当时,满足条件的正多边形的组合为4个正方形;2个正方形,1个正三角形,1个正六边形;2个正三角形、2个正六边形.
凸多边形
凹多边形
凸多边形
凹多边形
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
