2.4.1有理数的加法与减法:加法、加法运算律(同步课件)(苏科版2024)
文档属性
| 名称 | 2.4.1有理数的加法与减法:加法、加法运算律(同步课件)(苏科版2024) |  | |
| 格式 | pptx | ||
| 文件大小 | 10.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-29 09:12:45 | ||
图片预览











文档简介
(共37张PPT)
第2章 有理数
2.4.1 有理数的加法与减法:
加法、加法运算律
教学目标
01
贴近生活实例感受有理数的加法,理解有理数加法法则
03
02
熟悉有理数加法运算律
能灵活运用有理数加法法则和加法运算律进行运算
有理数的加法
01
课堂引入
小学里,我们学过非负有理数的加法和减法运算,引入负数后,怎样进行有理数的加法和减法运算呢?
+10
+
(+50)
=
+60
小明:我收到了来自马云先生发出的2个红包
小明
共收到60元
小明的账单:
01
课堂引入
-10
+
(-50)
=
-60
小明:我也给马云先生发2个红包
小明
共发出60元
小明的账单:
01
课堂引入
小明:咱们玩发红包游戏,我发一个,你发一个
小明发出
马云发出
-50
+
(+100)
=
+50
小明的账单:
01
课堂引入
小明:我发一个,你发一个,again
小明发出
马云发出
-100
+
(+10)
=
-90
小明的账单:
01
课堂引入
小明:我发一个,你发一个,again and again
小明发出
马云发出
-100
+
(+100)
=
0
小明的账单:
01
课堂引入
【总结】
正数+正数=____________________________;
负数+负数=____________________________;
负数+正数=____________________________。
想要掌握确切的规律,我们可以借助其他生活实例进一步分析~
正数
+10+(+50)=+60
-10+(-50)=-60
-50+100=+50
-100+10=-90
-100+100=0
负数
可能负数,可能正数,可能是0
01
课堂引入
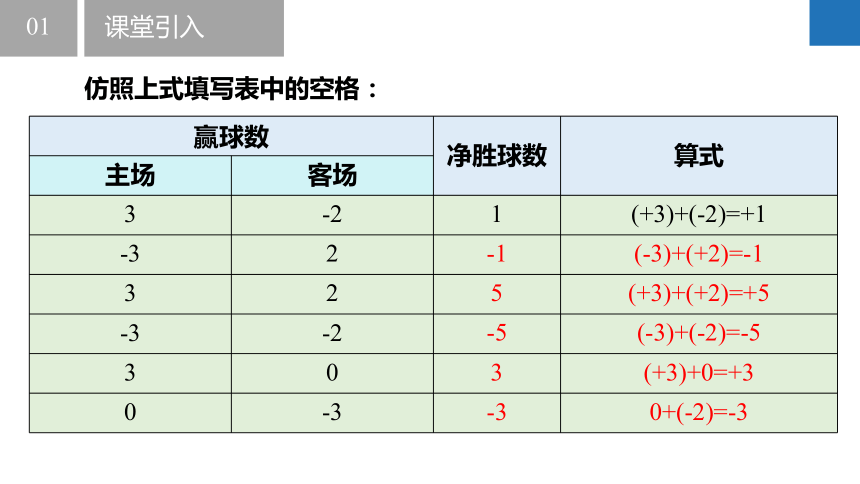
问题——在主客场制的足球排位赛中,当两队积分相同时,如何计算球队的净胜球数?
01
课堂引入
某支球队主场赢了3球,记作“+3”,客场输了2球,记作“-2”,则该队两场比赛的净胜球数为+1,可以用加法算式表示为:
(+3)+(-2)=+1
上式表示+3与-2两个数相加的和为+1,即净胜球数为1。
仿照上式填写表中的空格:
赢球数 净胜球数 算式
主场 客场 3 -2 1 (+3)+(-2)=+1
-3 2
3 2
-3 -2
3 0
0 -3
01
课堂引入
-1 (-3)+(+2)=-1
5 (+3)+(+2)=+5
-5 (-3)+(-2)=-5
3 (+3)+0=+3
-3 0+(-2)=-3
情境引入
1.第一个加数前若有符号,此加数可以带括号也可以不带括号
2.第二个加数前若有符号,必须要带括号
Pay attention to 算式书写格式
(-3)+-2=-5
(-3)+(-2)=-5
-3+(-2)=-5
两个符号不可以直接靠在一起,要用括号隔开
根据引入中的算式,我们分情况讨论两个有理数相加的情况:
02
知识精讲
1.两个加数的符号相同。
eg:(+3)+(+2)=+5,(-3)+(-2)=-5。
可以看出,和的符号与加数的符号________,
和的绝对值等于两个加数的绝对值之________。
一致
和
1
2
3
4
-1
0
5
+5
+3
+2
1
-4
-1
-2
-3
0
-5
-3
-2
-5
02
知识精讲
2.两个加数的符号不同。
eg:(+3)+(-2)=+1,(-3)+(+2)=-1。
此时,和的符号与绝对值较________的加数的符号一致,
和的绝对值等于________________________________。
大
较大的绝对值减去较小的绝对值
1
2
3
-1
-2
0
+3
-2
+1
1
2
-1
-2
-3
0
+2
-3
-1
02
知识精讲
eg:-100+(+100)=0。
若两加数的绝对值相等,则结果等于_____,
即互为相反数的两个数的和为_____。
0
0
1
2
3
-1
-2
0
+3
-3
02
知识精讲
2.两个加数中有一个是0。
eg:(+3)+0=+3,0+(-3)=-3。
此时,结果等于另一个数,即一个数加0,结果还是________。
这个数
1
2
3
-1
-2
0
+3
+3
1
2
-1
-2
-3
0
-3
-3
02
知识精讲
有理数加法法则
1.同号两数相加,
取相同的符号(定号),
并把绝对值相加(定值)。
2.异号两数相加,
①绝对值相等时,和为0;
②绝对值不等时,取绝对值较大的加数符号(定号),
并用较大的绝对值减去较小的绝对值(定值)。
3.一个数与0相加,仍得这个数。
例1、
算式 定号 定值 结果
(1)(+11)+4=
(2)(-11)+(-4)=
- 4.35+0.375 -4.725
+ 11+4 +15
- 11+4 -15
+
-
两个加数不同形,需要变同形
(5)原式=(-4.35)+(-0.375)
03
典例精析
例2、
算式 定号 定值 结果
(1) (+32)+(-14)=
(2)(+4)+(-9)=
(4)7+(-7)=
(5) (-9.75)+0=
+ 32-14 +18
- 9-4 -5
两个加数不同形,需要变同形
(5)原式=+(-)
-9.75
+ -4
0
03
典例精析
探究——对于任何一个数,加上一个数后,和比原来的数大还是小?为什么?
【分析】分3种情况讨论:
①一个数,加上一个正数,和比原来的数大;
a
0
正数
②一个数,加上0,和与原来的数相等;
③一个数,加上一个负数,和比原来的数小。
a
0
负数
03
典例精析
有理数加法运算律
1-1:黑板上两个算式的结果相等吗?
3
+ = _____
-5
3
+ = _____
-5
-2
-2
01
课堂引入
相等
相等,eg:(-4)+1=1+(-4)=-3,(-4)+(-1)=(-1)+(-4)=-5,……
1-2:把△、○中的数换成其他有理数,结果仍然相等吗?
1-1:黑板上两个算式的结果相等吗?
3
( + ) + = _____
-5
3
+ ( + ) = _____
-5
-7
-7
-9
-9
01
课堂引入
相等
相等,eg:[(-4)+1]+2=-4+(1+2)=-1,[(-4)+(-1)]+2=-4+[(-1)+2]=-3,……
1-2:把△、○、□中的数换成其他有理数,结果仍然相等吗?
事实上,小学里学过的加法交换律、结合律,在有理数范围内仍然适用。
加法运算律
02
知识精讲
有理数加法运算律
有理数加法运算律:
①交换律:a+b=b+a,
②结合律:(a+b)+c=a+(b+c)。
根据有理数加法运算律,在进行有理数加法运算时,可以交换加数的位置,也可以把其中几个数先相加。
例1、(+23)+(-25)+(+17)+(-14)=
解:原式=[(+23)+(+17)]+[(-25)+(-14)]
=(+40)+(-39)
=1
同号结合法
03
典例精析
例2、(-3.14)+(+4.96)+(+2.14)+(-7.96)=
解:原式=[(-3.14)+(+2.14)]+[(+4.96)+(-7.96)]
=(-1)+(-3)
=-4
凑整法
03
典例精析
例3、(-)+(+0.75)+(+)++1=
同分母结合法
03
典例精析
解:原式=[(-)+]+[(+)+(+)] +1
=(-)+(+)+1
=+1
=
例4、3+(-1.75)+2+(+1.75)+(-)=
相反数优先结合
03
典例精析
解:原式=(3+2)+[(-1.75)+(+1.75)] +(-)
=6+0+(-)
=
常用的结合技巧:
①同号加数结合法;②凑整法;
③同分母结合法;④相反数优先结合。
03
典例精析
有绝对值,要先计算绝对值
例5、-|-5|+0.25+(-6)+(-|-0.75|)=
解:原式=-5+0.25+(-6)+(-0.75)
=[-5+(-6)]+[0.25+(-0.75)]
=-11+(-0.5)
=-11.5
注意区分-|-5|和-(-5):
-|-5|=-5
-(-5)=5
03
典例精析
例6、|-2|+(-2.5)+1+|1+(-2)|=
建议将带分数化成假分数
03
典例精析
解:原式=|-|+(-2.5)+1+|1+(-)|
=+(-)+1+|-|
=0+1+
=
例7、-5+(-9)+17+(-3)=
若将带分数化成假分数,则本题的运算量过大,
此处给大家介绍一种新的方法:拆项法。
注意错误拆法:-5=-5+,×
03
典例精析
eg:-5=-(5+)=-5+(-),17=17+
例7、-5+(-9)+17+(-3)=
03
典例精析
解:原式=-5+(-)+(-9)+(-)+17++(-3)+(-)
=[-5+(-9)+17+(-3)]+[(-)+(-)++(-)]
=0+(-)
=-
课后总结
有理数加法法则:
1.同号两数相加,
取相同的符号(定号),
并把绝对值相加(定值)。
2.异号两数相加,
①绝对值相等时,和为0;
②绝对值不等时,取绝对值较大的加数符号(定号),
并用较大的绝对值减去较小的绝对值(定值)。
3.一个数与0相加,仍得这个数。
有理数加法运算律:
①交换律:a+b=b+a,
②结合律:(a+b)+c=a+(b+c)。
常用的结合技巧:
①同号加数结合法;
②凑整法;
③同分母结合法;
④相反数优先结合。
Thanks!
https://www.21cnjy.com/recruitment/home/fine
第2章 有理数
2.4.1 有理数的加法与减法:
加法、加法运算律
教学目标
01
贴近生活实例感受有理数的加法,理解有理数加法法则
03
02
熟悉有理数加法运算律
能灵活运用有理数加法法则和加法运算律进行运算
有理数的加法
01
课堂引入
小学里,我们学过非负有理数的加法和减法运算,引入负数后,怎样进行有理数的加法和减法运算呢?
+10
+
(+50)
=
+60
小明:我收到了来自马云先生发出的2个红包
小明
共收到60元
小明的账单:
01
课堂引入
-10
+
(-50)
=
-60
小明:我也给马云先生发2个红包
小明
共发出60元
小明的账单:
01
课堂引入
小明:咱们玩发红包游戏,我发一个,你发一个
小明发出
马云发出
-50
+
(+100)
=
+50
小明的账单:
01
课堂引入
小明:我发一个,你发一个,again
小明发出
马云发出
-100
+
(+10)
=
-90
小明的账单:
01
课堂引入
小明:我发一个,你发一个,again and again
小明发出
马云发出
-100
+
(+100)
=
0
小明的账单:
01
课堂引入
【总结】
正数+正数=____________________________;
负数+负数=____________________________;
负数+正数=____________________________。
想要掌握确切的规律,我们可以借助其他生活实例进一步分析~
正数
+10+(+50)=+60
-10+(-50)=-60
-50+100=+50
-100+10=-90
-100+100=0
负数
可能负数,可能正数,可能是0
01
课堂引入
问题——在主客场制的足球排位赛中,当两队积分相同时,如何计算球队的净胜球数?
01
课堂引入
某支球队主场赢了3球,记作“+3”,客场输了2球,记作“-2”,则该队两场比赛的净胜球数为+1,可以用加法算式表示为:
(+3)+(-2)=+1
上式表示+3与-2两个数相加的和为+1,即净胜球数为1。
仿照上式填写表中的空格:
赢球数 净胜球数 算式
主场 客场 3 -2 1 (+3)+(-2)=+1
-3 2
3 2
-3 -2
3 0
0 -3
01
课堂引入
-1 (-3)+(+2)=-1
5 (+3)+(+2)=+5
-5 (-3)+(-2)=-5
3 (+3)+0=+3
-3 0+(-2)=-3
情境引入
1.第一个加数前若有符号,此加数可以带括号也可以不带括号
2.第二个加数前若有符号,必须要带括号
Pay attention to 算式书写格式
(-3)+-2=-5
(-3)+(-2)=-5
-3+(-2)=-5
两个符号不可以直接靠在一起,要用括号隔开
根据引入中的算式,我们分情况讨论两个有理数相加的情况:
02
知识精讲
1.两个加数的符号相同。
eg:(+3)+(+2)=+5,(-3)+(-2)=-5。
可以看出,和的符号与加数的符号________,
和的绝对值等于两个加数的绝对值之________。
一致
和
1
2
3
4
-1
0
5
+5
+3
+2
1
-4
-1
-2
-3
0
-5
-3
-2
-5
02
知识精讲
2.两个加数的符号不同。
eg:(+3)+(-2)=+1,(-3)+(+2)=-1。
此时,和的符号与绝对值较________的加数的符号一致,
和的绝对值等于________________________________。
大
较大的绝对值减去较小的绝对值
1
2
3
-1
-2
0
+3
-2
+1
1
2
-1
-2
-3
0
+2
-3
-1
02
知识精讲
eg:-100+(+100)=0。
若两加数的绝对值相等,则结果等于_____,
即互为相反数的两个数的和为_____。
0
0
1
2
3
-1
-2
0
+3
-3
02
知识精讲
2.两个加数中有一个是0。
eg:(+3)+0=+3,0+(-3)=-3。
此时,结果等于另一个数,即一个数加0,结果还是________。
这个数
1
2
3
-1
-2
0
+3
+3
1
2
-1
-2
-3
0
-3
-3
02
知识精讲
有理数加法法则
1.同号两数相加,
取相同的符号(定号),
并把绝对值相加(定值)。
2.异号两数相加,
①绝对值相等时,和为0;
②绝对值不等时,取绝对值较大的加数符号(定号),
并用较大的绝对值减去较小的绝对值(定值)。
3.一个数与0相加,仍得这个数。
例1、
算式 定号 定值 结果
(1)(+11)+4=
(2)(-11)+(-4)=
- 4.35+0.375 -4.725
+ 11+4 +15
- 11+4 -15
+
-
两个加数不同形,需要变同形
(5)原式=(-4.35)+(-0.375)
03
典例精析
例2、
算式 定号 定值 结果
(1) (+32)+(-14)=
(2)(+4)+(-9)=
(4)7+(-7)=
(5) (-9.75)+0=
+ 32-14 +18
- 9-4 -5
两个加数不同形,需要变同形
(5)原式=+(-)
-9.75
+ -4
0
03
典例精析
探究——对于任何一个数,加上一个数后,和比原来的数大还是小?为什么?
【分析】分3种情况讨论:
①一个数,加上一个正数,和比原来的数大;
a
0
正数
②一个数,加上0,和与原来的数相等;
③一个数,加上一个负数,和比原来的数小。
a
0
负数
03
典例精析
有理数加法运算律
1-1:黑板上两个算式的结果相等吗?
3
+ = _____
-5
3
+ = _____
-5
-2
-2
01
课堂引入
相等
相等,eg:(-4)+1=1+(-4)=-3,(-4)+(-1)=(-1)+(-4)=-5,……
1-2:把△、○中的数换成其他有理数,结果仍然相等吗?
1-1:黑板上两个算式的结果相等吗?
3
( + ) + = _____
-5
3
+ ( + ) = _____
-5
-7
-7
-9
-9
01
课堂引入
相等
相等,eg:[(-4)+1]+2=-4+(1+2)=-1,[(-4)+(-1)]+2=-4+[(-1)+2]=-3,……
1-2:把△、○、□中的数换成其他有理数,结果仍然相等吗?
事实上,小学里学过的加法交换律、结合律,在有理数范围内仍然适用。
加法运算律
02
知识精讲
有理数加法运算律
有理数加法运算律:
①交换律:a+b=b+a,
②结合律:(a+b)+c=a+(b+c)。
根据有理数加法运算律,在进行有理数加法运算时,可以交换加数的位置,也可以把其中几个数先相加。
例1、(+23)+(-25)+(+17)+(-14)=
解:原式=[(+23)+(+17)]+[(-25)+(-14)]
=(+40)+(-39)
=1
同号结合法
03
典例精析
例2、(-3.14)+(+4.96)+(+2.14)+(-7.96)=
解:原式=[(-3.14)+(+2.14)]+[(+4.96)+(-7.96)]
=(-1)+(-3)
=-4
凑整法
03
典例精析
例3、(-)+(+0.75)+(+)++1=
同分母结合法
03
典例精析
解:原式=[(-)+]+[(+)+(+)] +1
=(-)+(+)+1
=+1
=
例4、3+(-1.75)+2+(+1.75)+(-)=
相反数优先结合
03
典例精析
解:原式=(3+2)+[(-1.75)+(+1.75)] +(-)
=6+0+(-)
=
常用的结合技巧:
①同号加数结合法;②凑整法;
③同分母结合法;④相反数优先结合。
03
典例精析
有绝对值,要先计算绝对值
例5、-|-5|+0.25+(-6)+(-|-0.75|)=
解:原式=-5+0.25+(-6)+(-0.75)
=[-5+(-6)]+[0.25+(-0.75)]
=-11+(-0.5)
=-11.5
注意区分-|-5|和-(-5):
-|-5|=-5
-(-5)=5
03
典例精析
例6、|-2|+(-2.5)+1+|1+(-2)|=
建议将带分数化成假分数
03
典例精析
解:原式=|-|+(-2.5)+1+|1+(-)|
=+(-)+1+|-|
=0+1+
=
例7、-5+(-9)+17+(-3)=
若将带分数化成假分数,则本题的运算量过大,
此处给大家介绍一种新的方法:拆项法。
注意错误拆法:-5=-5+,×
03
典例精析
eg:-5=-(5+)=-5+(-),17=17+
例7、-5+(-9)+17+(-3)=
03
典例精析
解:原式=-5+(-)+(-9)+(-)+17++(-3)+(-)
=[-5+(-9)+17+(-3)]+[(-)+(-)++(-)]
=0+(-)
=-
课后总结
有理数加法法则:
1.同号两数相加,
取相同的符号(定号),
并把绝对值相加(定值)。
2.异号两数相加,
①绝对值相等时,和为0;
②绝对值不等时,取绝对值较大的加数符号(定号),
并用较大的绝对值减去较小的绝对值(定值)。
3.一个数与0相加,仍得这个数。
有理数加法运算律:
①交换律:a+b=b+a,
②结合律:(a+b)+c=a+(b+c)。
常用的结合技巧:
①同号加数结合法;
②凑整法;
③同分母结合法;
④相反数优先结合。
Thanks!
https://www.21cnjy.com/recruitment/home/fine
同课章节目录
