11.3角的平分线的性质
文档属性
| 名称 | 11.3角的平分线的性质 |

|
|
| 格式 | rar | ||
| 文件大小 | 171.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-09-26 00:00:00 | ||
图片预览

文档简介
课件15张PPT。11.3角平分线的性质(1)伊敏河镇学校
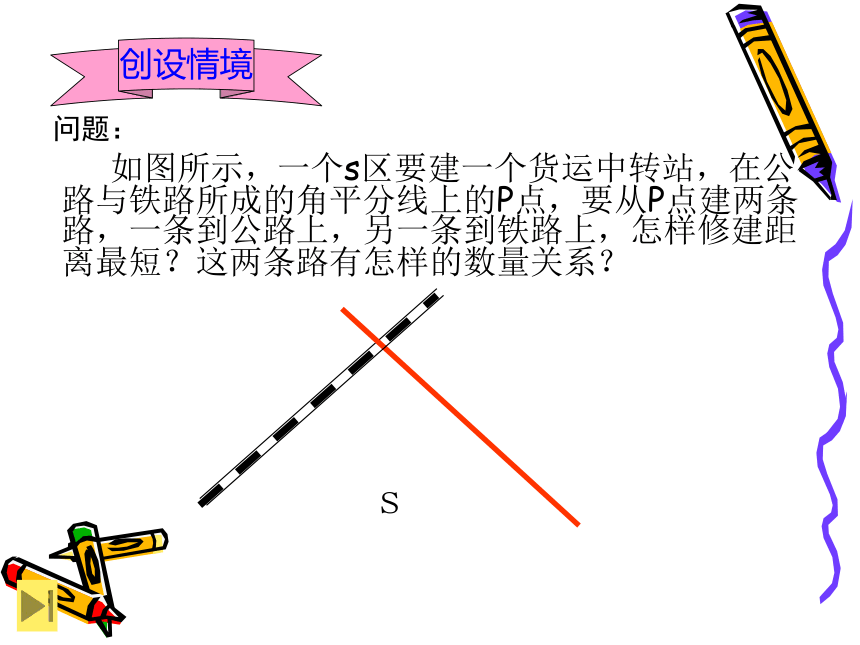
薄艳明2009.9.21问题:
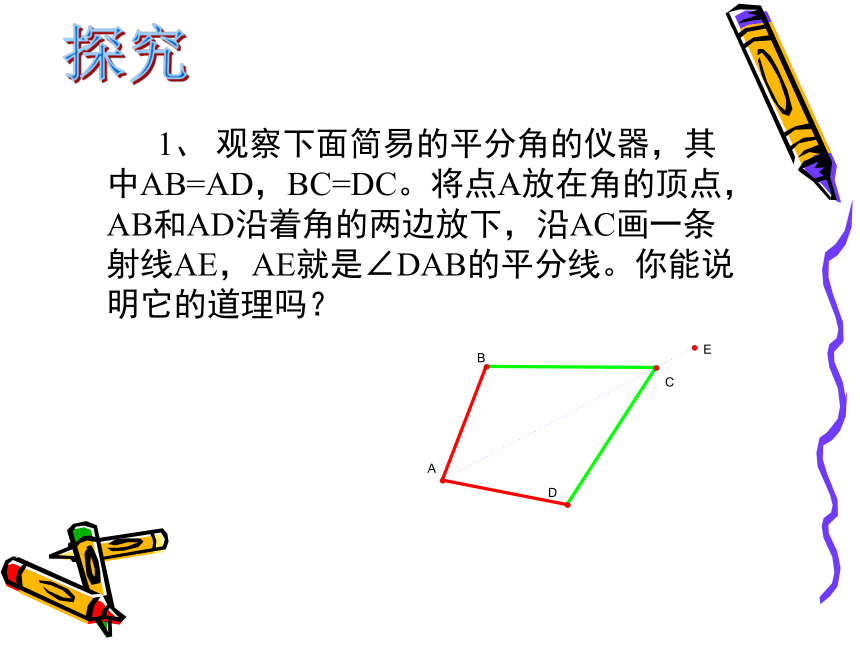
如图所示,一个s区要建一个货运中转站,在公路与铁路所成的角平分线上的P点,要从P点建两条路,一条到公路上,另一条到铁路上,怎样修建距离最短?这两条路有怎样的数量关系?创设情境 1、 观察下面简易的平分角的仪器,其中AB=AD,BC=DC。将点A放在角的顶点,AB和AD沿着角的两边放下,沿AC画一条射线AE,AE就是∠DAB的平分线。你能说明它的道理吗?探究 在△ADC和△ABC 中
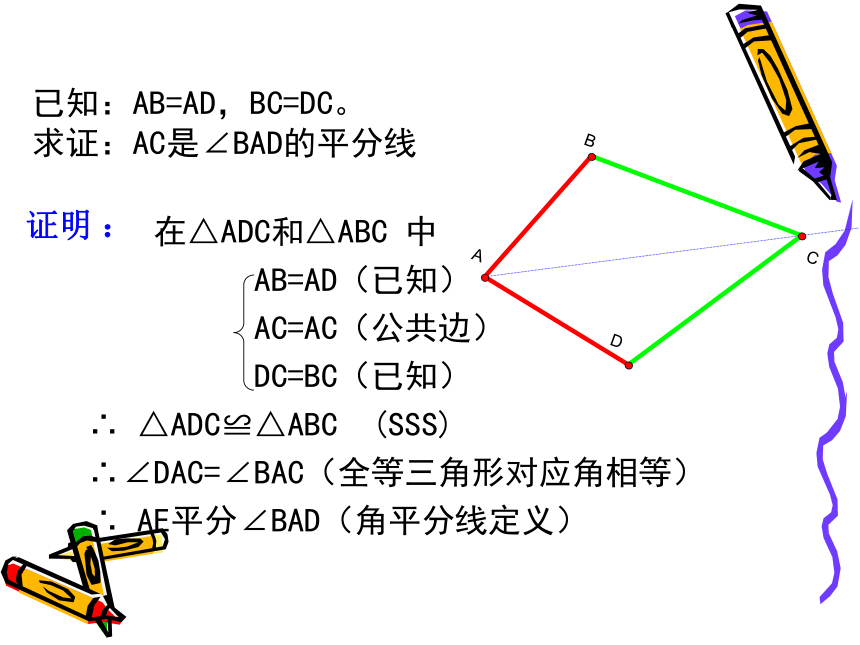
AB=AD(已知)
AC=AC(公共边)
DC=BC(已知)
∴ △ADC≌△ABC (SSS)
∴∠DAC=∠BAC(全等三角形对应角相等)
∴ AE平分∠BAD(角平分线定义)
证明 :已知:AB=AD,BC=DC。
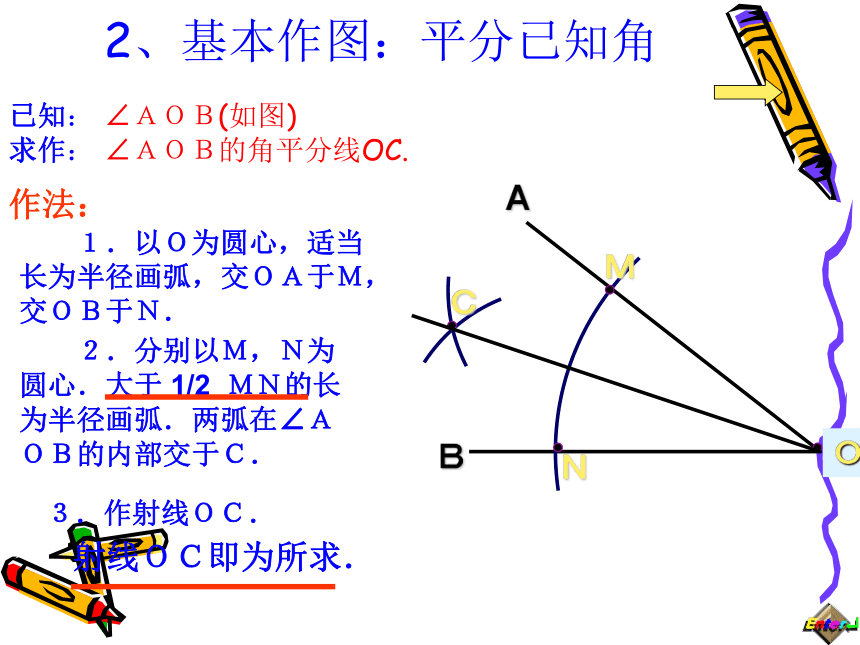
求证:AC是∠BAD的平分线2、基本作图:平分已知角 已知: ∠AOB(如图)
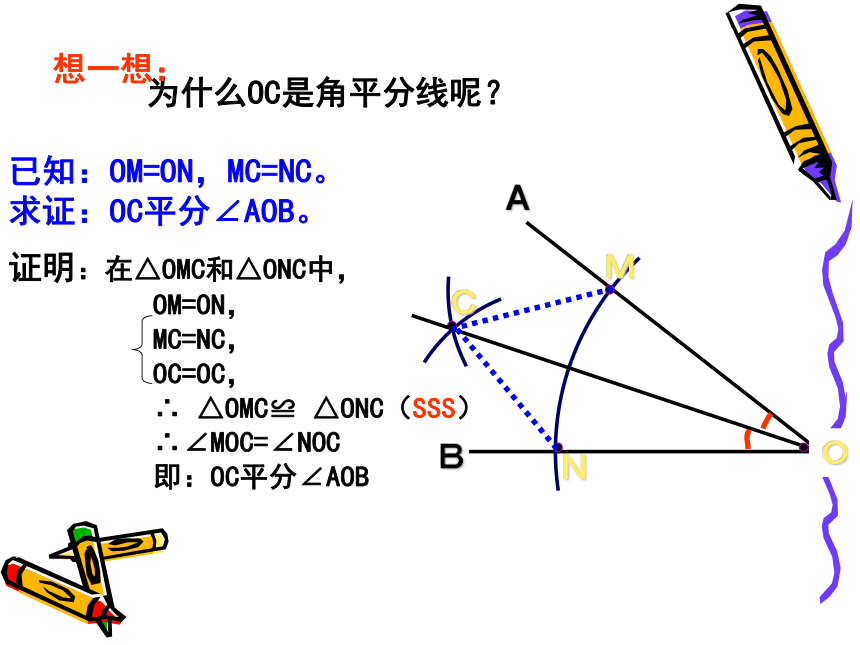
求作: ∠AOB的角平分线OC.AB作法: 1.以O为圆心,适当长为半径画弧,交OA于M,交OB于N. 2.分别以M,N为圆心.大于 1/2 MN的长为半径画弧.两弧在∠AOB的内部交于C.3.作射线OC.射线OC即为所求.AB为什么OC是角平分线呢? O想一想:已知:OM=ON,MC=NC。
求证:OC平分∠AOB。证明:在△OMC和△ONC中,
OM=ON,
MC=NC,
OC=OC,
∴ △OMC≌ △ONC(SSS)
∴∠MOC=∠NOC
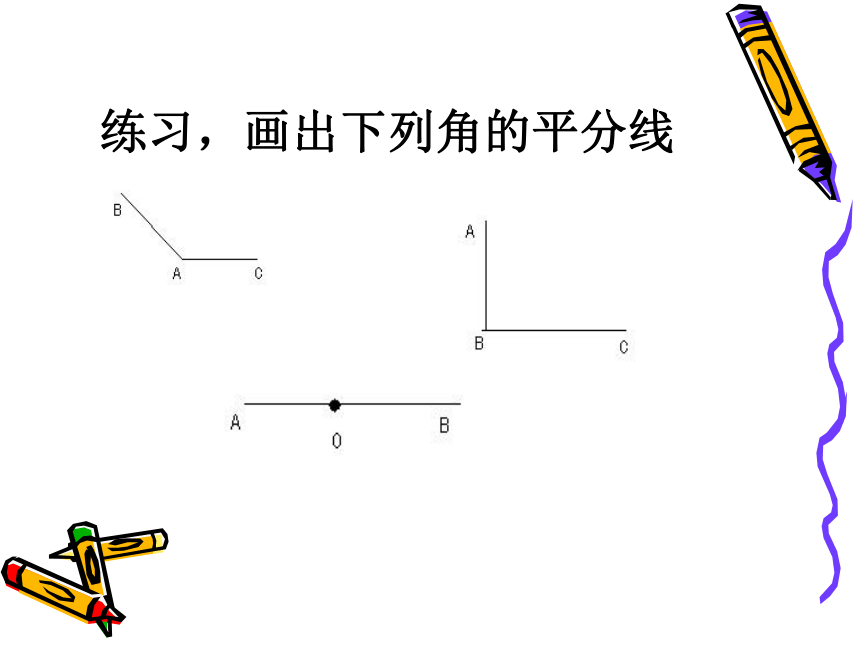
即:OC平分∠AOB练习,画出下列角的平分线思考:平分平角AOB。通过上面的步骤得到射线OC后,把它反向延长得到直线CD。直线CD与直线AB有什么关系?则我们得到作一条直线垂线的方法.
3、观察折纸,思考问题:将角AOB对折,再折出一个直角三角形(使第一条折痕为斜边),然后展开,观察两次折叠形成的三条折痕,你能得到什么结论?
1、折痕PE和PD与角的两边OA、OB有什么关系? PD和PE相等吗?
2、两次折叠形成的两个直角三角形全等吗?
3、由此你能得出关于角平分线的结论吗?并证明你的结论角平分线性质:
角平分线上的点到这个角的两边距离相等.
已知:(如图)OC平分∠AOB, P是OC上一点, PD⊥OA,PE⊥OB
求证:PD=PE
证明:∵ OC平分∠AOB, P是OC上一点(已知)
∴∠DOP=∠BOP(角平分线定义)
∵PD⊥OA,PE⊥OB (已知)
∴∠ODP=∠OEP=90°(垂直的定义)
在△OPD和△OPE 中
∠DOP=∠BOP (已证)
∠ODP=∠OEP (已证)
OP=OP (已知)
∴ △ADC≌△ABC (AAS)
∴PD=PE(全等三角形对应边相等)
几何语言:
∵OC是∠AOB的平分线,PD⊥OA,PE⊥OB
∴PD=PE(角平分线上的点到这个角的两边距离相等). 证明几何命题的步骤:教材P21明确命题中的已知和求证;
根据题意,画出图形,并用数学符号表示已知和求证;
经过分析,找出由已知推出求证的途径,写出证明过程。
已知:如图,△ABC中,∠C=90°,AD是△ABC的角平分线,DE⊥AB于E,F在AC上BD=DF,
求证:CF=EB。应用与提高证明:
∵ AD平分∠CAB
DE⊥AB,∠C=90°(已知)
∴ CD=DE (角平分线的性质)
在Rt△CDF和Rt△EDB中,
CD=DE (已证)
DF=DB (已知)
∴ Rt△CDF≌Rt△EDB (HL)
∴ CF=EB (全等三角形对应边相等)1、如图,连接角平分仪的
边BD、AC,那么AC与BD
有什么关系?为什么?提高与拓展 小结:这节课我们学到了什么?
1、角平分线的作法
作业:教材22页11.3复习巩固第2题
2、角平分线的性质
谢谢!
薄艳明2009.9.21问题:
如图所示,一个s区要建一个货运中转站,在公路与铁路所成的角平分线上的P点,要从P点建两条路,一条到公路上,另一条到铁路上,怎样修建距离最短?这两条路有怎样的数量关系?创设情境 1、 观察下面简易的平分角的仪器,其中AB=AD,BC=DC。将点A放在角的顶点,AB和AD沿着角的两边放下,沿AC画一条射线AE,AE就是∠DAB的平分线。你能说明它的道理吗?探究 在△ADC和△ABC 中
AB=AD(已知)
AC=AC(公共边)
DC=BC(已知)
∴ △ADC≌△ABC (SSS)
∴∠DAC=∠BAC(全等三角形对应角相等)
∴ AE平分∠BAD(角平分线定义)
证明 :已知:AB=AD,BC=DC。
求证:AC是∠BAD的平分线2、基本作图:平分已知角 已知: ∠AOB(如图)
求作: ∠AOB的角平分线OC.AB作法: 1.以O为圆心,适当长为半径画弧,交OA于M,交OB于N. 2.分别以M,N为圆心.大于 1/2 MN的长为半径画弧.两弧在∠AOB的内部交于C.3.作射线OC.射线OC即为所求.AB为什么OC是角平分线呢? O想一想:已知:OM=ON,MC=NC。
求证:OC平分∠AOB。证明:在△OMC和△ONC中,
OM=ON,
MC=NC,
OC=OC,
∴ △OMC≌ △ONC(SSS)
∴∠MOC=∠NOC
即:OC平分∠AOB练习,画出下列角的平分线思考:平分平角AOB。通过上面的步骤得到射线OC后,把它反向延长得到直线CD。直线CD与直线AB有什么关系?则我们得到作一条直线垂线的方法.
3、观察折纸,思考问题:将角AOB对折,再折出一个直角三角形(使第一条折痕为斜边),然后展开,观察两次折叠形成的三条折痕,你能得到什么结论?
1、折痕PE和PD与角的两边OA、OB有什么关系? PD和PE相等吗?
2、两次折叠形成的两个直角三角形全等吗?
3、由此你能得出关于角平分线的结论吗?并证明你的结论角平分线性质:
角平分线上的点到这个角的两边距离相等.
已知:(如图)OC平分∠AOB, P是OC上一点, PD⊥OA,PE⊥OB
求证:PD=PE
证明:∵ OC平分∠AOB, P是OC上一点(已知)
∴∠DOP=∠BOP(角平分线定义)
∵PD⊥OA,PE⊥OB (已知)
∴∠ODP=∠OEP=90°(垂直的定义)
在△OPD和△OPE 中
∠DOP=∠BOP (已证)
∠ODP=∠OEP (已证)
OP=OP (已知)
∴ △ADC≌△ABC (AAS)
∴PD=PE(全等三角形对应边相等)
几何语言:
∵OC是∠AOB的平分线,PD⊥OA,PE⊥OB
∴PD=PE(角平分线上的点到这个角的两边距离相等). 证明几何命题的步骤:教材P21明确命题中的已知和求证;
根据题意,画出图形,并用数学符号表示已知和求证;
经过分析,找出由已知推出求证的途径,写出证明过程。
已知:如图,△ABC中,∠C=90°,AD是△ABC的角平分线,DE⊥AB于E,F在AC上BD=DF,
求证:CF=EB。应用与提高证明:
∵ AD平分∠CAB
DE⊥AB,∠C=90°(已知)
∴ CD=DE (角平分线的性质)
在Rt△CDF和Rt△EDB中,
CD=DE (已证)
DF=DB (已知)
∴ Rt△CDF≌Rt△EDB (HL)
∴ CF=EB (全等三角形对应边相等)1、如图,连接角平分仪的
边BD、AC,那么AC与BD
有什么关系?为什么?提高与拓展 小结:这节课我们学到了什么?
1、角平分线的作法
作业:教材22页11.3复习巩固第2题
2、角平分线的性质
谢谢!
