11.1.2三角形的高、中线与角平分线 导学案(无答案)人教版数学八年级上册
文档属性
| 名称 | 11.1.2三角形的高、中线与角平分线 导学案(无答案)人教版数学八年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 217.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-26 00:00:00 | ||
图片预览

文档简介
三角形的高、中线与角平分线
【学习目标】
1.理解三角形的高、中线与角平分线的概念,了解三角形的稳定性.
2.会用工具准确画出三角形的高、中线与角平分线.
重点:三角形的高、中线与角平分线的特征.
难点:三角形的高、中线与角平分线的应用.
一、基础知识
1.三角形的高
2.三角形的中线
3.三角形角平分线
训练:1.按要求画出下列三角形的中线、高线、角平分线.
画中线AD,BE,CF 画高DG,EH,FM 画角平分线GM,HN,IP
2.几何语言表示三角形的高、中线、角平分线
几何推理 图例
三角形的高 ∵AD是△ABC的高, ∴①____⊥_____, ②∠ADB=∠______=______°
三角形的中线 ∵CF是△ABC的中线, ∴①AF=_____=______AC. ②AC=____AF=____CF. CB
三角形 的角平分线 ∵BE为△ABC的角平分线, ∴①∠1=∠_____=____∠ABC. ②∠ABC=____∠1=___∠2.
二、例题精选
【例1】在RtΔABC中,∠ACB=90°,AC=8,BC=6,AB=10.求AB边上高.
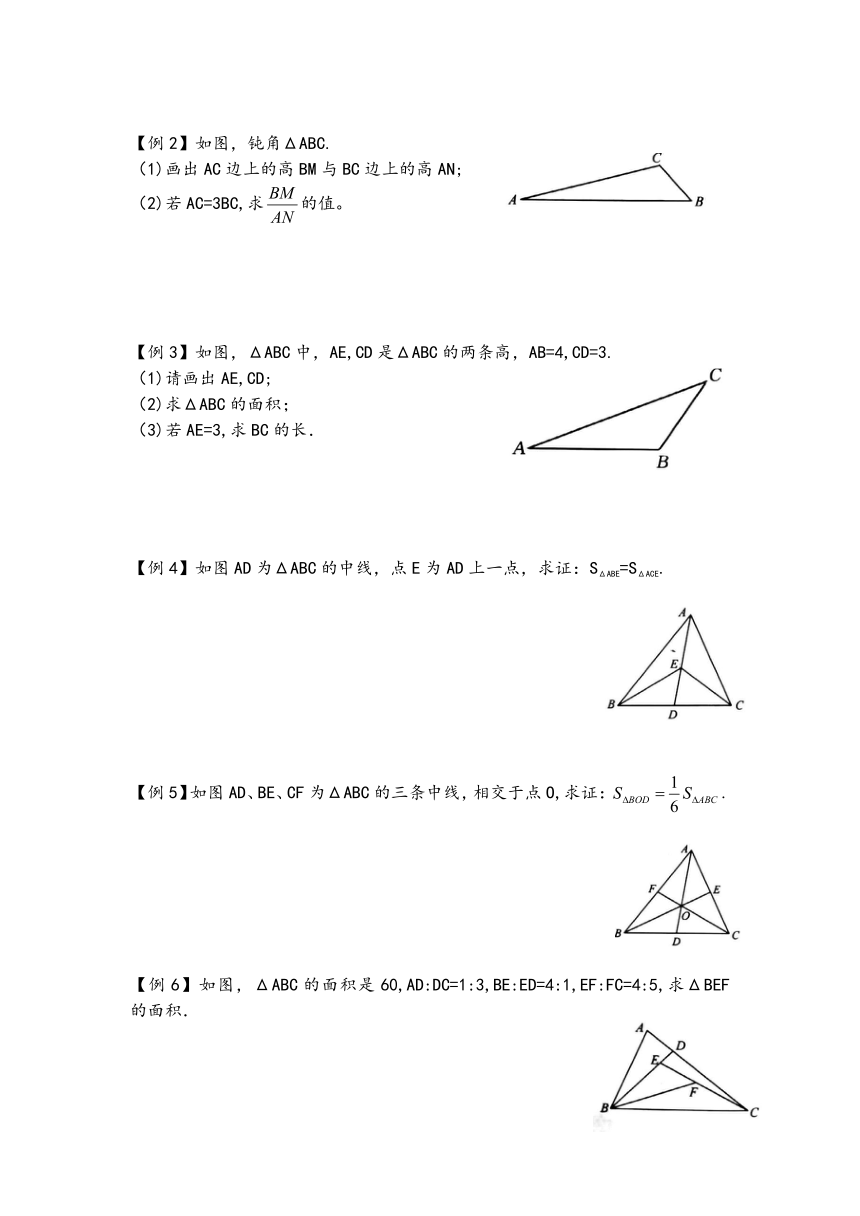
【例2】如图,钝角ΔABC.
(1)画出AC边上的高BM与BC边上的高AN;
(2)若AC=3BC,求的值。
【例3】如图,ΔABC中,AE,CD是ΔABC的两条高,AB=4,CD=3.
(1)请画出AE,CD;
(2)求ΔABC的面积;
(3)若AE=3,求BC的长.
【例4】如图AD为ΔABC的中线,点E为AD上一点,求证:SΔABE=SΔACE.
【例5】如图AD、BE、CF为ΔABC的三条中线,相交于点O,求证:.
【例6】如图,ΔABC的面积是60,AD:DC=1:3,BE:ED=4:1,EF:FC=4:5,求ΔBEF的面积.
【例7】如图,在△ABC中,E是BC上的一点,EC=2BE,点D是AC的中点,设△ABC,△ADF和△BEF的面积分别为S△ABC,S△ADF和S△BEF,且S△ABC=12,求S△ADF-S△BEF的值.
【例8】在ΔABC中,AB=2,BC=4,CD⊥AB于点D.
(1)如图1,AE⊥BC于点E,求证:CD=2AE;
(2)如图2,P是AC上任意一点(点P不与A,C重合),过点P作PE⊥BC于点E,PF⊥AB于点F,求证:2PE+PF=CD;
(3)在(2)中,若P为AC的延长线上任意一点,其他条件不变,请你在备用图中画出图形,并探究线段PE,PF,CD之间的数量关系.
【例9】如图,长方形ABCE,长BC=12,AB=10,SΔDEF=24,求S阴影.
三、课后作业
1.下列说法正确的是( )
A.三角形三条高都在三角形内 B.三角形三条中线相交于一点
C.三角形的三条角平分线可能在三角形内,也可能在三角形外
D.三角形的角平分线是射线
2.在△ABC中,AD为中线,BE为角平分线,则在以下等式中:①∠BAD=∠CAD;②∠ABE=∠CBE;③BD=DC;④AE=EC.其中正确的是 ( )
A.①② B.③④ C.①④ D.②③
3.如图,△ABC中∠C=90°,CD⊥AB,图中线段中可以作为△ABC的高的有 ( )
A.2条 B.3条 C.4条 D.5条
4.画△ABC中AB边上的高,下列画法中正确的是( )
A B C D
5.(1) ∵BE是△ABC的角平分线,
∴____ = _____= _____.
(2)∵CF是△ABC的角平分线,
∴∠ACB= 2______= 2______.
6.如图,AD是△ABC的中线,CE是△ACD的中线,S△AEC=3cm2,则S△ABC=____.
7.如图,ΔABC中,D,E分别为BC,AD的中点,SΔABC=20,则阴影部分的面积是( )
A.18 B.10 C.5 D.1
9.如图,在ΔABC中,已知点D,E,F分别为边BC,AD,CE的中点,且SΔABC=16cm2,则S阴影等于( )
A.8cm2 B.4cm2 C.2cm2 D.1cm2
10.如图,ΔABC中,D是AB的中点,且AE:CE=3:1,S△CEP=1,
则S△BPC=________.
11.在ΔABC中,AB=AC,,DB为ΔABC的中线,且BD将ΔABC周长分为12cm与15cm两部分,求三角形各边的长.
7.在△ABC中,CD是中线,已知BC-AC=5cm, △DBC的周长为25cm,求△ADC的周长.
12.如图,点O是等腰ΔAB底边BC上任意一点,过O作OE⊥AB于E,作OF⊥AC于F,若OE+OF=3,ΔABC的面积为12,则AB=_______.
13.如图,在ΔABC中,E为AC的中点,D为BC上一点,BD:CD=2:5,AD和BE交于点0,若SΔAOE-SΔBOD=5,求ΔABC的面积.
【学习目标】
1.理解三角形的高、中线与角平分线的概念,了解三角形的稳定性.
2.会用工具准确画出三角形的高、中线与角平分线.
重点:三角形的高、中线与角平分线的特征.
难点:三角形的高、中线与角平分线的应用.
一、基础知识
1.三角形的高
2.三角形的中线
3.三角形角平分线
训练:1.按要求画出下列三角形的中线、高线、角平分线.
画中线AD,BE,CF 画高DG,EH,FM 画角平分线GM,HN,IP
2.几何语言表示三角形的高、中线、角平分线
几何推理 图例
三角形的高 ∵AD是△ABC的高, ∴①____⊥_____, ②∠ADB=∠______=______°
三角形的中线 ∵CF是△ABC的中线, ∴①AF=_____=______AC. ②AC=____AF=____CF. CB
三角形 的角平分线 ∵BE为△ABC的角平分线, ∴①∠1=∠_____=____∠ABC. ②∠ABC=____∠1=___∠2.
二、例题精选
【例1】在RtΔABC中,∠ACB=90°,AC=8,BC=6,AB=10.求AB边上高.
【例2】如图,钝角ΔABC.
(1)画出AC边上的高BM与BC边上的高AN;
(2)若AC=3BC,求的值。
【例3】如图,ΔABC中,AE,CD是ΔABC的两条高,AB=4,CD=3.
(1)请画出AE,CD;
(2)求ΔABC的面积;
(3)若AE=3,求BC的长.
【例4】如图AD为ΔABC的中线,点E为AD上一点,求证:SΔABE=SΔACE.
【例5】如图AD、BE、CF为ΔABC的三条中线,相交于点O,求证:.
【例6】如图,ΔABC的面积是60,AD:DC=1:3,BE:ED=4:1,EF:FC=4:5,求ΔBEF的面积.
【例7】如图,在△ABC中,E是BC上的一点,EC=2BE,点D是AC的中点,设△ABC,△ADF和△BEF的面积分别为S△ABC,S△ADF和S△BEF,且S△ABC=12,求S△ADF-S△BEF的值.
【例8】在ΔABC中,AB=2,BC=4,CD⊥AB于点D.
(1)如图1,AE⊥BC于点E,求证:CD=2AE;
(2)如图2,P是AC上任意一点(点P不与A,C重合),过点P作PE⊥BC于点E,PF⊥AB于点F,求证:2PE+PF=CD;
(3)在(2)中,若P为AC的延长线上任意一点,其他条件不变,请你在备用图中画出图形,并探究线段PE,PF,CD之间的数量关系.
【例9】如图,长方形ABCE,长BC=12,AB=10,SΔDEF=24,求S阴影.
三、课后作业
1.下列说法正确的是( )
A.三角形三条高都在三角形内 B.三角形三条中线相交于一点
C.三角形的三条角平分线可能在三角形内,也可能在三角形外
D.三角形的角平分线是射线
2.在△ABC中,AD为中线,BE为角平分线,则在以下等式中:①∠BAD=∠CAD;②∠ABE=∠CBE;③BD=DC;④AE=EC.其中正确的是 ( )
A.①② B.③④ C.①④ D.②③
3.如图,△ABC中∠C=90°,CD⊥AB,图中线段中可以作为△ABC的高的有 ( )
A.2条 B.3条 C.4条 D.5条
4.画△ABC中AB边上的高,下列画法中正确的是( )
A B C D
5.(1) ∵BE是△ABC的角平分线,
∴____ = _____= _____.
(2)∵CF是△ABC的角平分线,
∴∠ACB= 2______= 2______.
6.如图,AD是△ABC的中线,CE是△ACD的中线,S△AEC=3cm2,则S△ABC=____.
7.如图,ΔABC中,D,E分别为BC,AD的中点,SΔABC=20,则阴影部分的面积是( )
A.18 B.10 C.5 D.1
9.如图,在ΔABC中,已知点D,E,F分别为边BC,AD,CE的中点,且SΔABC=16cm2,则S阴影等于( )
A.8cm2 B.4cm2 C.2cm2 D.1cm2
10.如图,ΔABC中,D是AB的中点,且AE:CE=3:1,S△CEP=1,
则S△BPC=________.
11.在ΔABC中,AB=AC,,DB为ΔABC的中线,且BD将ΔABC周长分为12cm与15cm两部分,求三角形各边的长.
7.在△ABC中,CD是中线,已知BC-AC=5cm, △DBC的周长为25cm,求△ADC的周长.
12.如图,点O是等腰ΔAB底边BC上任意一点,过O作OE⊥AB于E,作OF⊥AC于F,若OE+OF=3,ΔABC的面积为12,则AB=_______.
13.如图,在ΔABC中,E为AC的中点,D为BC上一点,BD:CD=2:5,AD和BE交于点0,若SΔAOE-SΔBOD=5,求ΔABC的面积.
