人教版数学八年级下册专项练习四勾股定理(含答案)
文档属性
| 名称 | 人教版数学八年级下册专项练习四勾股定理(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 355.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-26 16:49:49 | ||
图片预览

文档简介
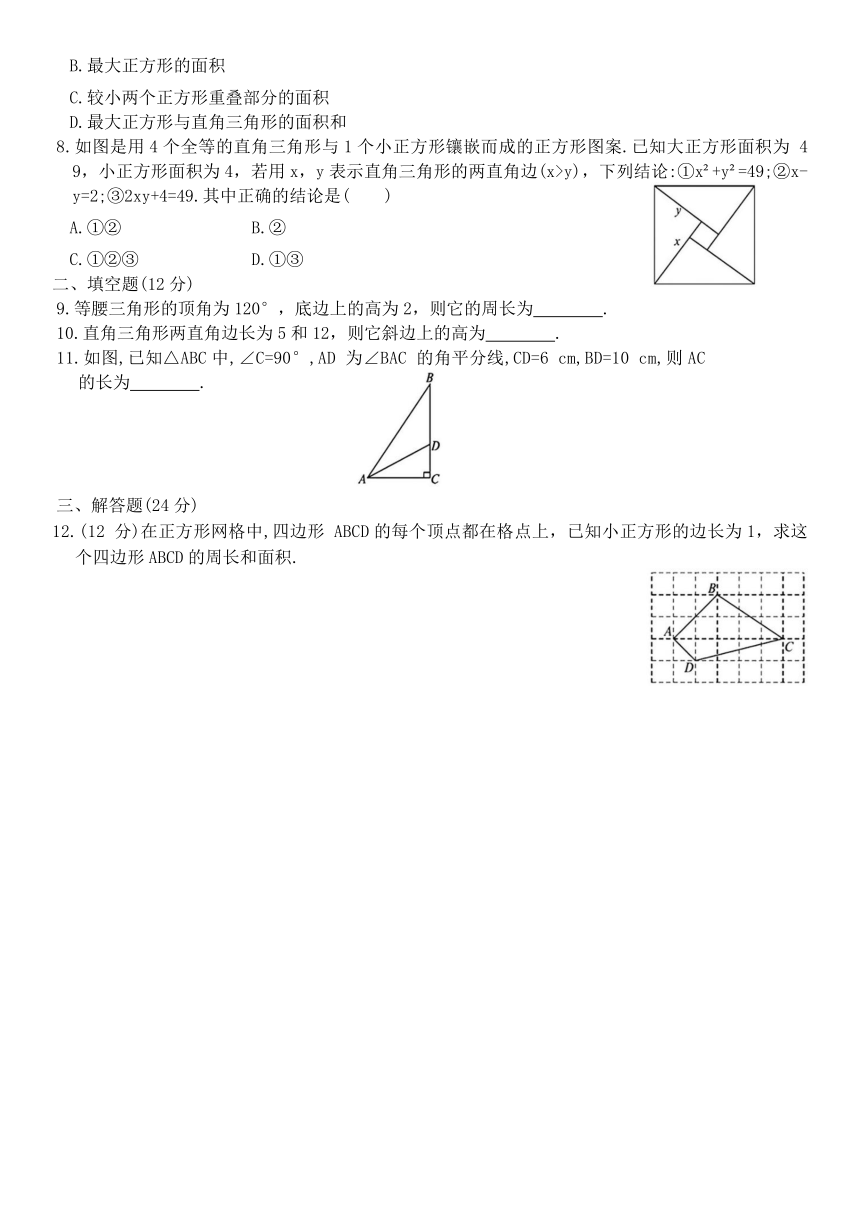
专项练习四 勾股定理
(限时:30分钟 满分:60分)
一、选择题(24分)
1.在Rt△ABC中,∠C=90°,a=8,c=10,则b的长是( )
A.4 B.
C.6
2. 在Rt△ABC中,a=3,b=5,则c的长为( )
A.2
C.4 D.4或
3.若一个等腰三角形的腰长为5,底边长为6,则底边上的高为( )
A.4 B.3
C.5 D.6
4.如图,在△ABC中,AB⊥AC,AB=5cm ,BC=13 cm,BD 是 AC 边上的中线,则△BCD的面积是( )
D. 65 cm
5.如图,点 A,B,C在正方形网格中的格点上,每个小正方形的边长为1,则下列关于△ABC边长的说法,正确的是( )
A. AB,BC长均为有理数,AC长为无理数
B. AC长是有理数,AB,BC长均为无理数
C. AB 长是有理数,AC,BC长均为无理数
D.三边长均为无理数
6. 如图,△ABC 中,AB=AC=6,AE⊥AC,DE 垂直平分AB 于点D, 则EC的长为( )
7.勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载.如图1,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图2的方式放置在最大正方形内.若知道图中阴影部分的面积,则一定能求出( )
A.直角三角形的面积
B.最大正方形的面积
C.较小两个正方形重叠部分的面积
D.最大正方形与直角三角形的面积和
8.如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案.已知大正方形面积为 49,小正方形面积为4,若用x,y表示直角三角形的两直角边(x>y),下列结论:①x +y =49;②x-y=2;③2xy+4=49.其中正确的结论是( )
A.①② B.②
C.①②③ D.①③
二、填空题(12分)
9.等腰三角形的顶角为120°,底边上的高为2,则它的周长为 .
10.直角三角形两直角边长为5和12,则它斜边上的高为 .
11.如图,已知△ABC中,∠C=90°,AD 为∠BAC 的角平分线,CD=6 cm,BD=10 cm,则AC的长为 .
三、解答题(24分)
12.(12 分)在正方形网格中,四边形 ABCD的每个顶点都在格点上,已知小正方形的边长为1,求这个四边形ABCD的周长和面积.
13.(12分)如图,在 Rt△ABC中, AB的垂直平分线分别交AB、AC 于点D、E.求AB、EC的长.
专项练习四 勾股定理
1. C 2. D 3. A 4. A 5. B 6. B 7. C 8. C 10. / 11.12 cm
12.解: ∴这个四边形ABCD的周长 这个四边形ABCD的面积
13.解:连接BE.
在 Rt△ABC中,∠C=90°,AC=16,BC=12,
∵AB的垂直平分线分别交AB、AC于点D、E,
∴AE=BE.
设EC=x,则BE=AE=16-x,
∵Rt△ABC中,∠C=90°,BC=12,
解得
(限时:30分钟 满分:60分)
一、选择题(24分)
1.在Rt△ABC中,∠C=90°,a=8,c=10,则b的长是( )
A.4 B.
C.6
2. 在Rt△ABC中,a=3,b=5,则c的长为( )
A.2
C.4 D.4或
3.若一个等腰三角形的腰长为5,底边长为6,则底边上的高为( )
A.4 B.3
C.5 D.6
4.如图,在△ABC中,AB⊥AC,AB=5cm ,BC=13 cm,BD 是 AC 边上的中线,则△BCD的面积是( )
D. 65 cm
5.如图,点 A,B,C在正方形网格中的格点上,每个小正方形的边长为1,则下列关于△ABC边长的说法,正确的是( )
A. AB,BC长均为有理数,AC长为无理数
B. AC长是有理数,AB,BC长均为无理数
C. AB 长是有理数,AC,BC长均为无理数
D.三边长均为无理数
6. 如图,△ABC 中,AB=AC=6,AE⊥AC,DE 垂直平分AB 于点D, 则EC的长为( )
7.勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载.如图1,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图2的方式放置在最大正方形内.若知道图中阴影部分的面积,则一定能求出( )
A.直角三角形的面积
B.最大正方形的面积
C.较小两个正方形重叠部分的面积
D.最大正方形与直角三角形的面积和
8.如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案.已知大正方形面积为 49,小正方形面积为4,若用x,y表示直角三角形的两直角边(x>y),下列结论:①x +y =49;②x-y=2;③2xy+4=49.其中正确的结论是( )
A.①② B.②
C.①②③ D.①③
二、填空题(12分)
9.等腰三角形的顶角为120°,底边上的高为2,则它的周长为 .
10.直角三角形两直角边长为5和12,则它斜边上的高为 .
11.如图,已知△ABC中,∠C=90°,AD 为∠BAC 的角平分线,CD=6 cm,BD=10 cm,则AC的长为 .
三、解答题(24分)
12.(12 分)在正方形网格中,四边形 ABCD的每个顶点都在格点上,已知小正方形的边长为1,求这个四边形ABCD的周长和面积.
13.(12分)如图,在 Rt△ABC中, AB的垂直平分线分别交AB、AC 于点D、E.求AB、EC的长.
专项练习四 勾股定理
1. C 2. D 3. A 4. A 5. B 6. B 7. C 8. C 10. / 11.12 cm
12.解: ∴这个四边形ABCD的周长 这个四边形ABCD的面积
13.解:连接BE.
在 Rt△ABC中,∠C=90°,AC=16,BC=12,
∵AB的垂直平分线分别交AB、AC于点D、E,
∴AE=BE.
设EC=x,则BE=AE=16-x,
∵Rt△ABC中,∠C=90°,BC=12,
解得
