人教版数学八年级下册 专项练习九 菱形(含答案)
文档属性
| 名称 | 人教版数学八年级下册 专项练习九 菱形(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 489.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-26 17:13:43 | ||
图片预览

文档简介
专项练习九 菱形
(限时:30分钟 满分:60分)
一、选择题(24分)
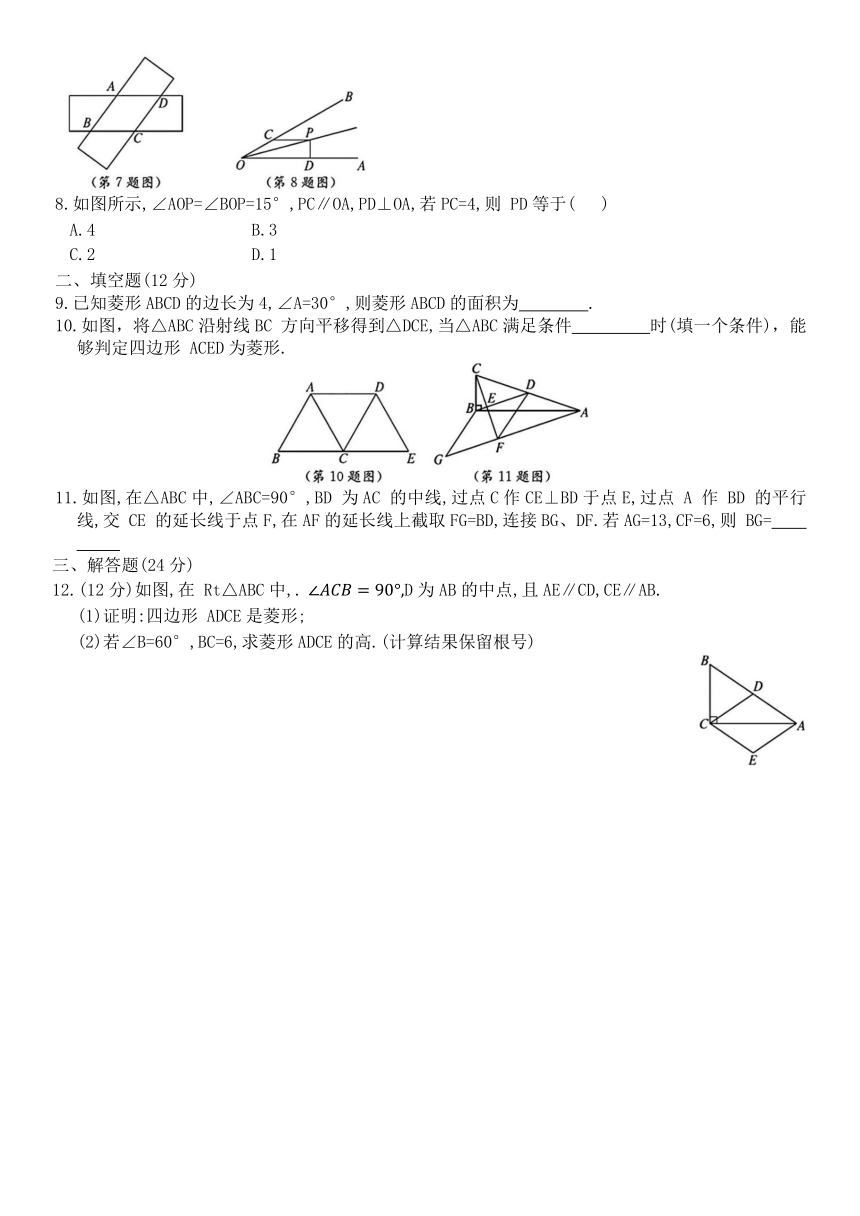
1.如图,菱形ABCD的周长为 20,对角线 AC与BD交于点 O,BD=6,则AC等于( )
A.6 B.8 C.10 D.12
2.如图,菱形ABCD中,∠D=150°,则∠1=( )
A.30° B.25° C.20° D.15°
3.如图,在 ABCD中,AC与BD交于点O,下列判断中不正确的是( )
A.若AB=BC,则 ABCD是菱形
B.若AC⊥BD,则 ABCD 是菱形
C.若AC平分∠BAD,则 ABCD是菱形
D.若AC=BD,则 ABCD是菱形
4.如图,△ABC中,DE∥BC,EF∥AB,要判定四边形 DBFE 是菱形,还需要添加的条件是( )
A. BE平分∠ABC B. AD=BD
C. BE⊥AC D. AB=AC
5.如图,等边△ABC沿射线BC 向右平移到△DCE 的位置,连接 AD、BD,则下列结论:①AD=BC;②BD、AC互相平分;③四边形 ACED 是菱形;④∠ACD=∠DCE.其中正确的个数是( )
A.1 B.2 C.3 D.4
6.如图,已知四边形ABCD的四边相等,等边△AMN的顶点 M、N 分别在BC、CD 上,且AM=AB,则∠C为( )
A.100° B.105°
C. 110° D.120°
7.如图,两张等宽的纸条交叉重叠在一起,重叠的部分为四边形ABCD,若测得A,C之间的距离为 12 cm,点 B,D 之间的距离为16 cm,则线段AB 的长为( )
A.9.6 cm B.10 cm
C.20 cm D.12 cm
8.如图所示,∠AOP=∠BOP=15°,PC∥OA,PD⊥OA,若PC=4,则 PD等于( )
A.4 B.3
C.2 D.1
二、填空题(12分)
9.已知菱形ABCD的边长为4,∠A=30°,则菱形ABCD的面积为 .
10.如图,将△ABC沿射线BC 方向平移得到△DCE,当△ABC满足条件 时(填一个条件),能够判定四边形 ACED为菱形.
11.如图,在△ABC中,∠ABC=90°,BD 为AC 的中线,过点C作CE⊥BD于点E,过点 A 作 BD 的平行线,交 CE 的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.若AG=13,CF=6,则 BG=
三、解答题(24分)
12.(12分)如图,在 Rt△ABC中,. D为AB的中点,且AE∥CD,CE∥AB.
(1)证明:四边形 ADCE是菱形;
(2)若∠B=60°,BC=6,求菱形ADCE的高.(计算结果保留根号)
13.(12 分)如图,在四边形 ABCD 中,AD∥BC,BA=BC,BD平分∠ABC.
(1)求证:四边形ABCD 是菱形;
(2)过点 D 作 DE⊥BD,交 BC的延长线于点E,若BC=5,BD=8,求四边形ABED的周长.
专项练习九 菱形
1. B 2. D 3. D 4. A 5. D 6. A 7. B 8. C9.810. AC=BC 11.5
12.(1)证明:
∴四边形ADCE是平行四边形.
又∵∠ACB=90°,D是AB的中点,
∴平行四边形 ADCE是菱形;
(2)解:过点 D作DF⊥CE,垂足为点F,如图所示:
DF即为菱形ADCE的高,
∵∠B=60°,CD=BD,
∴△BCD是等边三角形,
CD=BC=6,
∵CE∥AB,∴∠DCE=∠BDC=60°,又∵CD=BC=6,
∴在Rt△CDF中,
13.(1)证明:∵AD∥BC,∴∠ADB=∠CBD,
∵BD平分∠ABC,∴∠ABD=∠CBD,
∴∠ADB=∠ABD,∴AD=AB,
∵BA=BC,∴AD=BC,
∴四边形ABCD是平行四边形,
∵BA=BC,∴四边形ABCD是菱形;
(2)解:∵DE⊥BD,∴∠BDE=90°,
∴∠DBC+∠E=∠BDC+∠CDE=90°,
∵CB=CD,∴∠DBC=∠BDC,
∴∠CDE=∠E,∴CD=CE=BC,
∴BE=2BC=10,
∵四边形ABCD是菱形,∴AD=AB=BC=5,
∴四边形ABED的周长=AD+AB+BE+DE=26.
(限时:30分钟 满分:60分)
一、选择题(24分)
1.如图,菱形ABCD的周长为 20,对角线 AC与BD交于点 O,BD=6,则AC等于( )
A.6 B.8 C.10 D.12
2.如图,菱形ABCD中,∠D=150°,则∠1=( )
A.30° B.25° C.20° D.15°
3.如图,在 ABCD中,AC与BD交于点O,下列判断中不正确的是( )
A.若AB=BC,则 ABCD是菱形
B.若AC⊥BD,则 ABCD 是菱形
C.若AC平分∠BAD,则 ABCD是菱形
D.若AC=BD,则 ABCD是菱形
4.如图,△ABC中,DE∥BC,EF∥AB,要判定四边形 DBFE 是菱形,还需要添加的条件是( )
A. BE平分∠ABC B. AD=BD
C. BE⊥AC D. AB=AC
5.如图,等边△ABC沿射线BC 向右平移到△DCE 的位置,连接 AD、BD,则下列结论:①AD=BC;②BD、AC互相平分;③四边形 ACED 是菱形;④∠ACD=∠DCE.其中正确的个数是( )
A.1 B.2 C.3 D.4
6.如图,已知四边形ABCD的四边相等,等边△AMN的顶点 M、N 分别在BC、CD 上,且AM=AB,则∠C为( )
A.100° B.105°
C. 110° D.120°
7.如图,两张等宽的纸条交叉重叠在一起,重叠的部分为四边形ABCD,若测得A,C之间的距离为 12 cm,点 B,D 之间的距离为16 cm,则线段AB 的长为( )
A.9.6 cm B.10 cm
C.20 cm D.12 cm
8.如图所示,∠AOP=∠BOP=15°,PC∥OA,PD⊥OA,若PC=4,则 PD等于( )
A.4 B.3
C.2 D.1
二、填空题(12分)
9.已知菱形ABCD的边长为4,∠A=30°,则菱形ABCD的面积为 .
10.如图,将△ABC沿射线BC 方向平移得到△DCE,当△ABC满足条件 时(填一个条件),能够判定四边形 ACED为菱形.
11.如图,在△ABC中,∠ABC=90°,BD 为AC 的中线,过点C作CE⊥BD于点E,过点 A 作 BD 的平行线,交 CE 的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.若AG=13,CF=6,则 BG=
三、解答题(24分)
12.(12分)如图,在 Rt△ABC中,. D为AB的中点,且AE∥CD,CE∥AB.
(1)证明:四边形 ADCE是菱形;
(2)若∠B=60°,BC=6,求菱形ADCE的高.(计算结果保留根号)
13.(12 分)如图,在四边形 ABCD 中,AD∥BC,BA=BC,BD平分∠ABC.
(1)求证:四边形ABCD 是菱形;
(2)过点 D 作 DE⊥BD,交 BC的延长线于点E,若BC=5,BD=8,求四边形ABED的周长.
专项练习九 菱形
1. B 2. D 3. D 4. A 5. D 6. A 7. B 8. C9.810. AC=BC 11.5
12.(1)证明:
∴四边形ADCE是平行四边形.
又∵∠ACB=90°,D是AB的中点,
∴平行四边形 ADCE是菱形;
(2)解:过点 D作DF⊥CE,垂足为点F,如图所示:
DF即为菱形ADCE的高,
∵∠B=60°,CD=BD,
∴△BCD是等边三角形,
CD=BC=6,
∵CE∥AB,∴∠DCE=∠BDC=60°,又∵CD=BC=6,
∴在Rt△CDF中,
13.(1)证明:∵AD∥BC,∴∠ADB=∠CBD,
∵BD平分∠ABC,∴∠ABD=∠CBD,
∴∠ADB=∠ABD,∴AD=AB,
∵BA=BC,∴AD=BC,
∴四边形ABCD是平行四边形,
∵BA=BC,∴四边形ABCD是菱形;
(2)解:∵DE⊥BD,∴∠BDE=90°,
∴∠DBC+∠E=∠BDC+∠CDE=90°,
∵CB=CD,∴∠DBC=∠BDC,
∴∠CDE=∠E,∴CD=CE=BC,
∴BE=2BC=10,
∵四边形ABCD是菱形,∴AD=AB=BC=5,
∴四边形ABED的周长=AD+AB+BE+DE=26.
