湘教版数学八年级上册第1章 分式 综合素质评价 (含答案)
文档属性
| 名称 | 湘教版数学八年级上册第1章 分式 综合素质评价 (含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 56.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-26 17:52:26 | ||
图片预览


文档简介
第1章综合素质评价
一、选择题(每题3分,共30分)
1.下列各式不是分式的是( )
A. B. C. D.
2.要使分式有意义,则x的取值范围是( )
A. x>1 B. x≠1 C. x=1 D. x≠0
3.[2023·湖州母题·教材P6习题T1] 若分式的值为0,则x的值是( )
A.1 B.0 C.-1 D.-3
4.[2024·常德十一中月考]若a≠b,则下列分式化简正确的是( )
A. = B. = C. = D.=
5.下列各式计算结果为a5的是( )
A.(a3)2 B. a10÷a2 C. a4·a D.(-1)-1a5
6.生物学家发现了某种花粉的直径约为0.000 002 1毫米,数据0.000 002 1用科学记数法表示正确的是( )
A.2.1×10-6 B.21×10-6 C.2.1×10-5 D.21×10-5
7.分式方程=1的解是( )
A. x=6 B. x=-6 C. x=5 D. x=-5
8.[新考法整体代入法]如果a2+2a-1=0,那么·的值是( )
A.-3 B.-1 C.1 D.3
9.[2023·淄博]为贯彻落实习近平总书记关于黄河流域生态保护和高质量发展的重要讲话精神,某学校组织七、八两个年级学生到黄河岸边开展植树造林活动.已知七年级植树900棵与八年级植树1 200棵所用的时间相同,两个年级平均每小时共植树350棵.求七年级平均每小时植树多少棵.设七年级平均每小时植树x棵,则下面所列方程中正确的是( )
A.= B.= C.= D.=
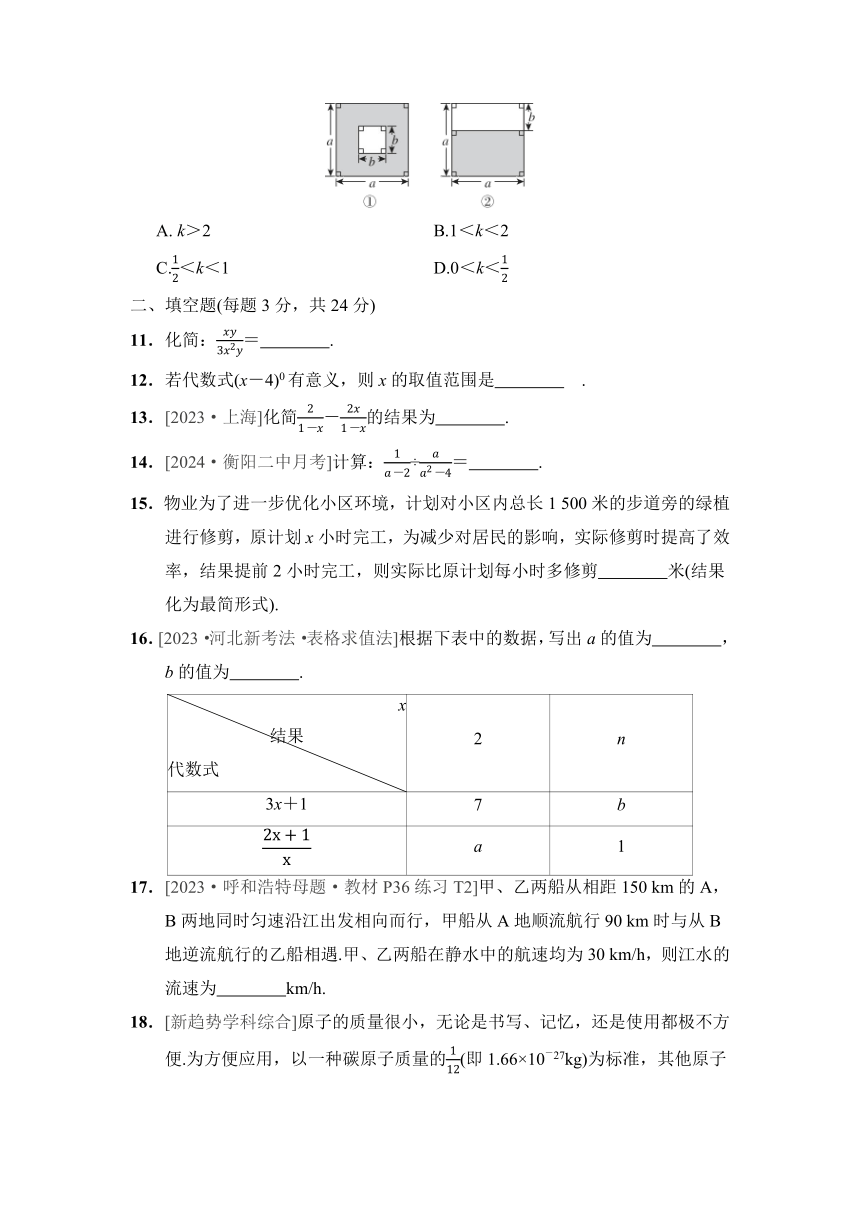
10.[2024·长沙南雅中学月考]如图,设k=(a>b>0),则有( )
A. k>2 B.1<k<2
C.<k<1 D.0<k<
二、填空题(每题3分,共24分)
11.化简:= .
12.若代数式(x-4)0有意义,则x的取值范围是 .
13.[2023·上海]化简-的结果为 .
14.[2024·衡阳二中月考]计算:÷= .
15.物业为了进一步优化小区环境,计划对小区内总长1 500米的步道旁的绿植进行修剪,原计划x小时完工,为减少对居民的影响,实际修剪时提高了效率,结果提前2小时完工,则实际比原计划每小时多修剪 米(结果化为最简形式).
16.[2023·河北新考法·表格求值法]根据下表中的数据,写出a的值为 ,b的值为 .
x 结果 代数式 2 n
3x+1 7 b
a 1
17.[2023·呼和浩特母题·教材P36练习T2]甲、乙两船从相距150 km的A,B两地同时匀速沿江出发相向而行,甲船从A地顺流航行90 km时与从B地逆流航行的乙船相遇.甲、乙两船在静水中的航速均为30 km/h,则江水的流速为 km/h.
18.[新趋势学科综合]原子的质量很小,无论是书写、记忆,还是使用都极不方便.为方便应用,以一种碳原子质量的(即1.66×10-27kg)为标准,其他原子的质量跟它相比所得到的比值,称为这种原子的相对原子质量.若一个碳原子的质量是1.992×10-26kg,则该碳原子的相对原子质量为 .
三、解答题(19题16分,20题10分,21,24题每题12分,22,23题每题8分,共66分)
19.[母题教材P39复习题T3]计算:
(1)|-7|-(1-π)0+; (2)·÷;
(3)[2023·衢州]+2; (4)[2023·襄阳]÷.
20.[母题教材P39复习题T7]解分式方程:
(1)[2023·广西]=; (2)-1=.
21.[2023·黄石新视角·条件选择题]先化简÷,然后从1,2,3,4中选择一个合适的数代入求值.
22.[母题教材P35例3]为营造良好体育运动氛围,某学校用800元购买了一批足球,又用1 560元加购了第二批足球,且所购数量是第一批购买数量的2倍,但单价降了2元,请问该学校两批共购买了多少个足球?
23.[2024·衡阳北斗星实验中学模拟]小华想复习分式方程,由于印刷问题,有一个数“?”看不清楚:+3=.
(1)她把这个数“?”猜成5,请你帮小华解这个分式方程.
(2)小华的妈妈说:“我看到标准答案是,方程的增根是x=2,原分式方程无解.”那么原分式方程中“?”代表的数是多少?
24.[新视角新定义型题]阅读理解:
定义:若分式A和分式B满足A-B=n(n为正整数),则称A是B的“n差分式”.
例如:-=3,我们称是的“3差分式”.
解答下列问题:
(1)分式是分式的“ 差分式”.
(2)分式A=是分式B=的“2差分式”.
①C= (用含x的代数式表示);
②若A的值为正整数,x为正整数,求A的值.
(3)已知xy=2,分式是-的“4差分式”(其中x,y均为正数),求(x-y)2的值.
答案
一、1. C 2. B 3. A 4. D 5. C 6. A 7. A
8. C 【点拨】·=·=(a+2)·a=a2+2a.因为a2+2a-1=0,所以原式=a2+2a=1,故选C.
9. D
10. B 【点拨】题图①中阴影部分面积为a2-b2,题图②中阴影部分面积为a(a-b).则k====1+.因为a>b>0,所以0<<1,所以1<1+<2,即1<k<2.故选B.
二、11. 12. x≠4
13.2 14. 15.
16.;-2 【点拨】当x=2时,=a,即a==.
当x=n时,=1,即=1,解得n=-1.
经检验,n=-1是分式方程的解.
当x=n时,3x+1=b,即3n+1=b,
所以b=3×(-1)+1=-2.
17.6 【点拨】设江水的流速为x km/h,根据题意,
得=.
解得x=6.经检验,x=6是原分式方程的解,且符合题意.
所以江水的流速为6 km/h.
18.12
三、19.【解】(1)原式=7-1+3=9.
(2)原式=··=-.
(3)原式=+2=a-2+2=a.
(4)原式=÷=·=.
20.【解】(1)方程两边同乘x(x-1),
得2x=x-1,解得x=-1.
检验:当x=-1时,x(x-1)=2≠0,
所以原分式方程的解为x=-1.
(2)方程两边同乘(x+1)(x-1),
得(x-1)x-(x+1)(x-1)=3(x+1),解得x=-.
检验:当x=-时,(x+1)(x-1)=-≠0,
所以原分式方程的解为x=-.
21.【解】÷
=·
=·
=.
因为m-3≠0,m-1≠0,
所以m≠3,m≠1.所以取m=2.
当m=2时,原式==-.(答案不唯一)
22.【解】设第一批足球的单价为x元,则第二批足球的单价为(x-2)元.
由题意得×2=,解得x=80.
经检验,x=80是原分式方程的解,且符合题意.
故第二批足球的单价为80-2=78(元),
所以+=30(个).
答:该学校两批共购买了30个足球.
23.【解】(1)把“?”=5代入原分式方程,得+3=.方程两边同时乘(x-2),得5+3(x-2)=-1,解得x=0.经检验,x=0是原分式方程的解.
(2)设“?”为m,则+3=,方程两边同时乘(x-2),得m+3(x-2)=-1.因为x=2是原分式方程的增根,所以把x=2代入上面的等式,得m+3×(2-2)=-1,即m=-1,所以原分式方程中“?”代表的数是-1.
24.【解】(1)1 【点拨】因为-==1,
所以分式是分式的“1差分式”.
(2)①18+6x 【点拨】因为分式A=是分式B=的“2差分式”,
所以-=2,即-=.
所以C-2x(3+x)=2(9-x2),
所以C=2x(3+x)+2(9-x2)=18+6x.
②因为A===,
且A的值为正整数,x为正整数,
所以3-x=1,2,3或6.
当3-x=1时,x=2;
当3-x=2时,x=1;
当3-x=3时,x=0(舍去);
当3-x=6时,x=-3(舍去).所以x=2或1.
当x=2时,A=6;当x=1时,A=3.
所以A的值为6或3.
(3)因为分式是-的“4差分式”(其中x,y均为正数),
所以-=4,则=4.
因为xy=2,
所以(x-y)2=8.
一、选择题(每题3分,共30分)
1.下列各式不是分式的是( )
A. B. C. D.
2.要使分式有意义,则x的取值范围是( )
A. x>1 B. x≠1 C. x=1 D. x≠0
3.[2023·湖州母题·教材P6习题T1] 若分式的值为0,则x的值是( )
A.1 B.0 C.-1 D.-3
4.[2024·常德十一中月考]若a≠b,则下列分式化简正确的是( )
A. = B. = C. = D.=
5.下列各式计算结果为a5的是( )
A.(a3)2 B. a10÷a2 C. a4·a D.(-1)-1a5
6.生物学家发现了某种花粉的直径约为0.000 002 1毫米,数据0.000 002 1用科学记数法表示正确的是( )
A.2.1×10-6 B.21×10-6 C.2.1×10-5 D.21×10-5
7.分式方程=1的解是( )
A. x=6 B. x=-6 C. x=5 D. x=-5
8.[新考法整体代入法]如果a2+2a-1=0,那么·的值是( )
A.-3 B.-1 C.1 D.3
9.[2023·淄博]为贯彻落实习近平总书记关于黄河流域生态保护和高质量发展的重要讲话精神,某学校组织七、八两个年级学生到黄河岸边开展植树造林活动.已知七年级植树900棵与八年级植树1 200棵所用的时间相同,两个年级平均每小时共植树350棵.求七年级平均每小时植树多少棵.设七年级平均每小时植树x棵,则下面所列方程中正确的是( )
A.= B.= C.= D.=
10.[2024·长沙南雅中学月考]如图,设k=(a>b>0),则有( )
A. k>2 B.1<k<2
C.<k<1 D.0<k<
二、填空题(每题3分,共24分)
11.化简:= .
12.若代数式(x-4)0有意义,则x的取值范围是 .
13.[2023·上海]化简-的结果为 .
14.[2024·衡阳二中月考]计算:÷= .
15.物业为了进一步优化小区环境,计划对小区内总长1 500米的步道旁的绿植进行修剪,原计划x小时完工,为减少对居民的影响,实际修剪时提高了效率,结果提前2小时完工,则实际比原计划每小时多修剪 米(结果化为最简形式).
16.[2023·河北新考法·表格求值法]根据下表中的数据,写出a的值为 ,b的值为 .
x 结果 代数式 2 n
3x+1 7 b
a 1
17.[2023·呼和浩特母题·教材P36练习T2]甲、乙两船从相距150 km的A,B两地同时匀速沿江出发相向而行,甲船从A地顺流航行90 km时与从B地逆流航行的乙船相遇.甲、乙两船在静水中的航速均为30 km/h,则江水的流速为 km/h.
18.[新趋势学科综合]原子的质量很小,无论是书写、记忆,还是使用都极不方便.为方便应用,以一种碳原子质量的(即1.66×10-27kg)为标准,其他原子的质量跟它相比所得到的比值,称为这种原子的相对原子质量.若一个碳原子的质量是1.992×10-26kg,则该碳原子的相对原子质量为 .
三、解答题(19题16分,20题10分,21,24题每题12分,22,23题每题8分,共66分)
19.[母题教材P39复习题T3]计算:
(1)|-7|-(1-π)0+; (2)·÷;
(3)[2023·衢州]+2; (4)[2023·襄阳]÷.
20.[母题教材P39复习题T7]解分式方程:
(1)[2023·广西]=; (2)-1=.
21.[2023·黄石新视角·条件选择题]先化简÷,然后从1,2,3,4中选择一个合适的数代入求值.
22.[母题教材P35例3]为营造良好体育运动氛围,某学校用800元购买了一批足球,又用1 560元加购了第二批足球,且所购数量是第一批购买数量的2倍,但单价降了2元,请问该学校两批共购买了多少个足球?
23.[2024·衡阳北斗星实验中学模拟]小华想复习分式方程,由于印刷问题,有一个数“?”看不清楚:+3=.
(1)她把这个数“?”猜成5,请你帮小华解这个分式方程.
(2)小华的妈妈说:“我看到标准答案是,方程的增根是x=2,原分式方程无解.”那么原分式方程中“?”代表的数是多少?
24.[新视角新定义型题]阅读理解:
定义:若分式A和分式B满足A-B=n(n为正整数),则称A是B的“n差分式”.
例如:-=3,我们称是的“3差分式”.
解答下列问题:
(1)分式是分式的“ 差分式”.
(2)分式A=是分式B=的“2差分式”.
①C= (用含x的代数式表示);
②若A的值为正整数,x为正整数,求A的值.
(3)已知xy=2,分式是-的“4差分式”(其中x,y均为正数),求(x-y)2的值.
答案
一、1. C 2. B 3. A 4. D 5. C 6. A 7. A
8. C 【点拨】·=·=(a+2)·a=a2+2a.因为a2+2a-1=0,所以原式=a2+2a=1,故选C.
9. D
10. B 【点拨】题图①中阴影部分面积为a2-b2,题图②中阴影部分面积为a(a-b).则k====1+.因为a>b>0,所以0<<1,所以1<1+<2,即1<k<2.故选B.
二、11. 12. x≠4
13.2 14. 15.
16.;-2 【点拨】当x=2时,=a,即a==.
当x=n时,=1,即=1,解得n=-1.
经检验,n=-1是分式方程的解.
当x=n时,3x+1=b,即3n+1=b,
所以b=3×(-1)+1=-2.
17.6 【点拨】设江水的流速为x km/h,根据题意,
得=.
解得x=6.经检验,x=6是原分式方程的解,且符合题意.
所以江水的流速为6 km/h.
18.12
三、19.【解】(1)原式=7-1+3=9.
(2)原式=··=-.
(3)原式=+2=a-2+2=a.
(4)原式=÷=·=.
20.【解】(1)方程两边同乘x(x-1),
得2x=x-1,解得x=-1.
检验:当x=-1时,x(x-1)=2≠0,
所以原分式方程的解为x=-1.
(2)方程两边同乘(x+1)(x-1),
得(x-1)x-(x+1)(x-1)=3(x+1),解得x=-.
检验:当x=-时,(x+1)(x-1)=-≠0,
所以原分式方程的解为x=-.
21.【解】÷
=·
=·
=.
因为m-3≠0,m-1≠0,
所以m≠3,m≠1.所以取m=2.
当m=2时,原式==-.(答案不唯一)
22.【解】设第一批足球的单价为x元,则第二批足球的单价为(x-2)元.
由题意得×2=,解得x=80.
经检验,x=80是原分式方程的解,且符合题意.
故第二批足球的单价为80-2=78(元),
所以+=30(个).
答:该学校两批共购买了30个足球.
23.【解】(1)把“?”=5代入原分式方程,得+3=.方程两边同时乘(x-2),得5+3(x-2)=-1,解得x=0.经检验,x=0是原分式方程的解.
(2)设“?”为m,则+3=,方程两边同时乘(x-2),得m+3(x-2)=-1.因为x=2是原分式方程的增根,所以把x=2代入上面的等式,得m+3×(2-2)=-1,即m=-1,所以原分式方程中“?”代表的数是-1.
24.【解】(1)1 【点拨】因为-==1,
所以分式是分式的“1差分式”.
(2)①18+6x 【点拨】因为分式A=是分式B=的“2差分式”,
所以-=2,即-=.
所以C-2x(3+x)=2(9-x2),
所以C=2x(3+x)+2(9-x2)=18+6x.
②因为A===,
且A的值为正整数,x为正整数,
所以3-x=1,2,3或6.
当3-x=1时,x=2;
当3-x=2时,x=1;
当3-x=3时,x=0(舍去);
当3-x=6时,x=-3(舍去).所以x=2或1.
当x=2时,A=6;当x=1时,A=3.
所以A的值为6或3.
(3)因为分式是-的“4差分式”(其中x,y均为正数),
所以-=4,则=4.
因为xy=2,
所以(x-y)2=8.
同课章节目录
