湘教版数学八年级上册第2章 三角形 综合素质评价(含答案)
文档属性
| 名称 | 湘教版数学八年级上册第2章 三角形 综合素质评价(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 373.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-26 17:54:10 | ||
图片预览



文档简介
第2章综合素质评价
一、选择题(每题3分,共30分)
1.[2023·衡阳母题·教材P44练习T2]下列长度的各组线段能组成一个三角形的是( )
A.1 cm,2 cm,3 cm B.3 cm,8 cm,5 cm
C.4 cm,5 cm,10 cm D.4 cm,5 cm,6 cm
2.[2023·宿迁]若等腰三角形有一个内角为110°,则这个等腰三角形的底角是( )
A.70° B.45° C.35° D.50°
3.[2023·青岛]如图,直线a∥b,∠1=63°,∠B=45°,则∠2的度数为( )
(第3题)
A.105° B.108° C.117° D.135°
4.[母题教材P59习题T3] 下列命题是真命题的是( )
A.两个锐角之和一定是钝角
B.三角形的任意两边之和大于第三边
C.内错角相等
D.三角形的重心是这个三角形的三条角平分线的交点
5.[2024·湖南师范大学附中月考]如图,在等边三角形ABC中,AD⊥BC,垂足为D,点E在线段AD上,∠EBC=45°,则∠ACE等于( )
(第5题)
A.15° B.30° C.45° D.60°
6.根据下列已知条件,能画出唯一的△ABC的是( )
A. AB=3,BC=4,AC=7 B. AB=4,BC=3,∠A=30°
C.∠A=∠B,AB=6 D.∠A=60°,∠B=45°,AC=4
7.[2023·盐城]小华将一副三角板(∠C=∠D=90°,∠B=30°,∠E=45°)按如图所示的方式摆放,其中AB∥EF,则∠1的度数为( )
(第7题)
A.45° B.60° C.75° D.105°
8.如图,在△ABC中,AD是BC边上的中线,CE是AB边上的高,若AB=4,S△ABD=6,则CE的长是( )
(第8题)
A.3 B.4 C.6 D.8
9.如图,将△ABC沿DE折叠,使点A落在A'处,则∠1+∠2与∠A的关系是( )
(第9题)
A.∠1+∠2=∠A B.∠1+∠2=2∠A
C.2(∠1+∠2)=3∠A D.∠1+∠2=
10.如图,D是△ABC的边BC上一点,DE交AB于点F,连接AE,AD,已知AD=AC,∠EAB=∠CAD=∠BDE,下列结论不一定正确的是( )
(第10题)
A. AB=AE B.∠B=∠E C.∠B=∠DAF D. DE=BC
二、填空题(每题3分,共24分)
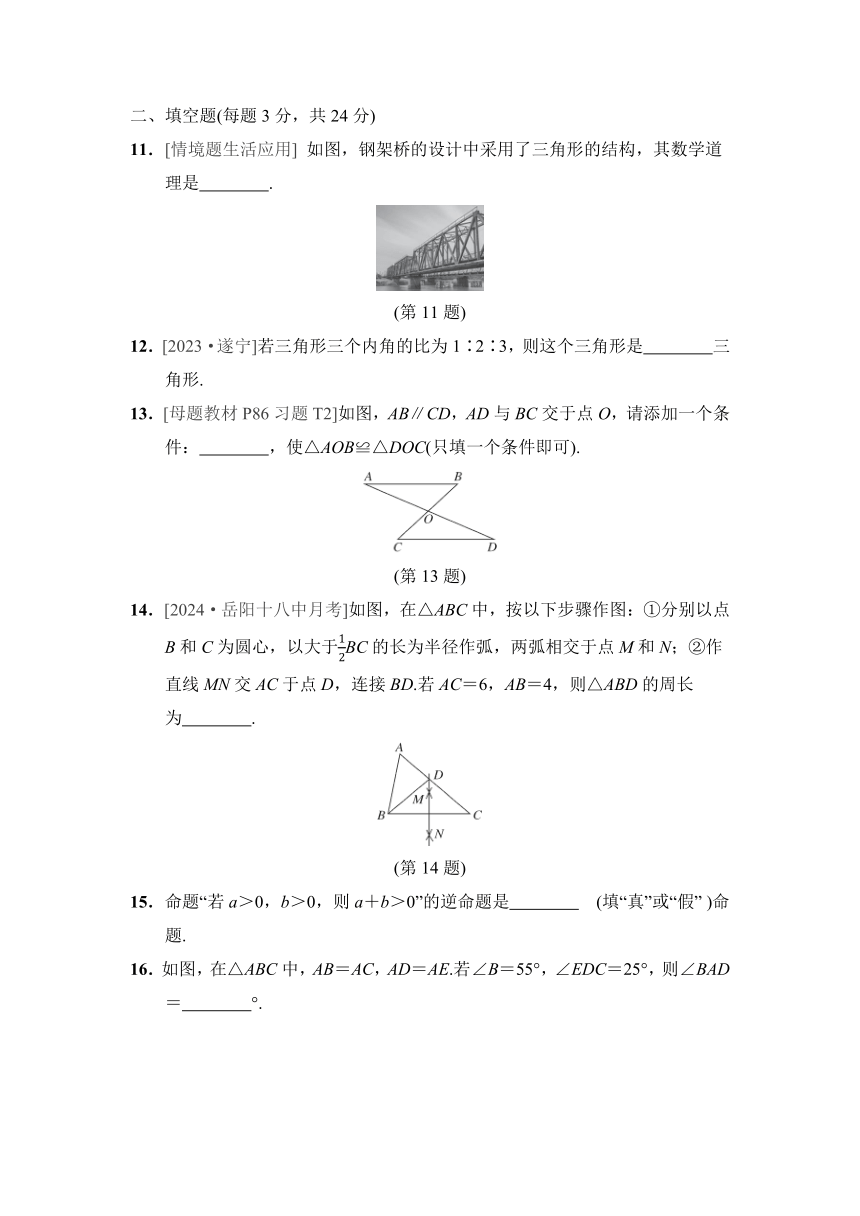
11.[情境题生活应用] 如图,钢架桥的设计中采用了三角形的结构,其数学道理是 .
(第11题)
12.[2023·遂宁]若三角形三个内角的比为1∶2∶3,则这个三角形是 三角形.
13.[母题教材P86习题T2]如图,AB∥CD,AD与BC交于点O,请添加一个条件: ,使△AOB≌△DOC(只填一个条件即可).
(第13题)
14.[2024·岳阳十八中月考]如图,在△ABC中,按以下步骤作图:①分别以点B和C为圆心,以大于BC的长为半径作弧,两弧相交于点M和N;②作直线MN交AC于点D,连接BD.若AC=6,AB=4,则△ABD的周长为 .
(第14题)
15.命题“若a>0,b>0,则a+b>0”的逆命题是 (填“真”或“假” )命题.
16.如图,在△ABC中,AB=AC,AD=AE.若∠B=55°,∠EDC=25°,则∠BAD= °.
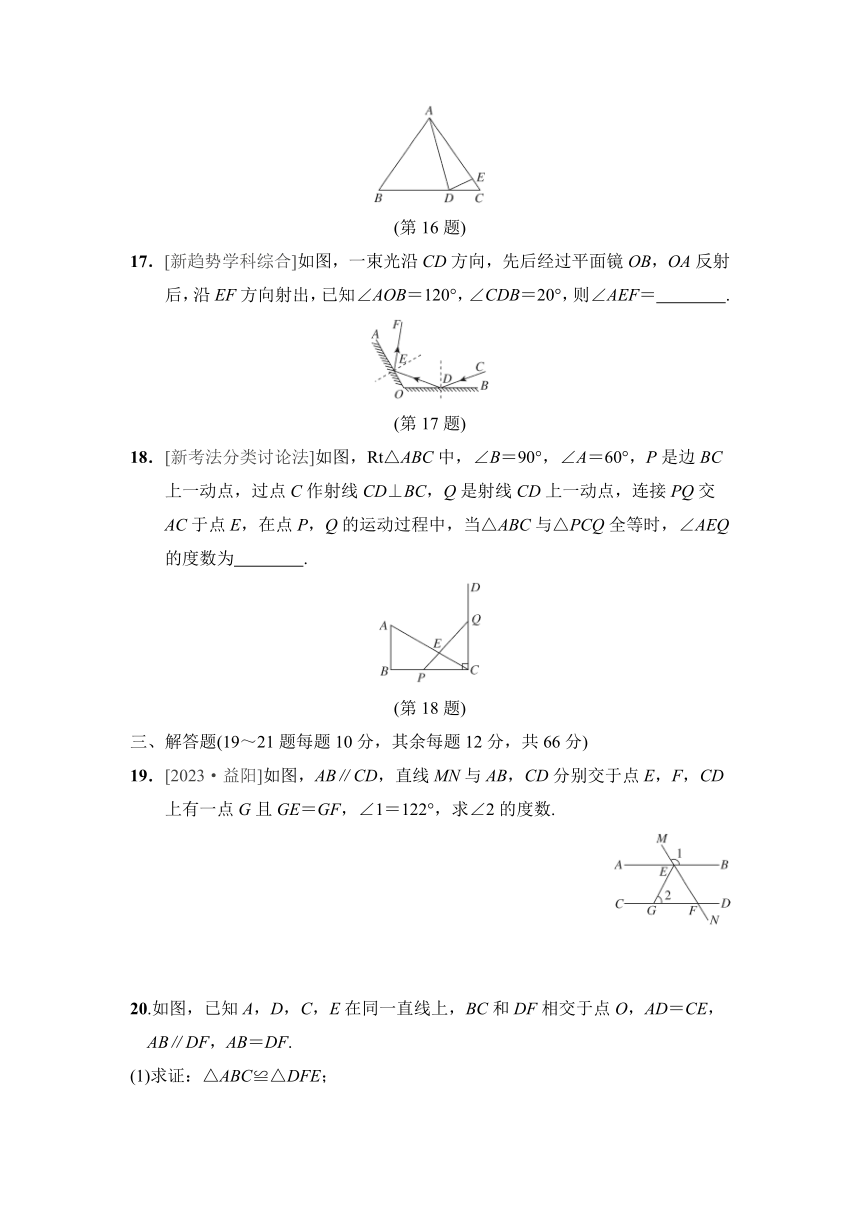
(第16题)
17.[新趋势学科综合]如图,一束光沿CD方向,先后经过平面镜OB,OA反射后,沿EF方向射出,已知∠AOB=120°,∠CDB=20°,则∠AEF= .
(第17题)
18.[新考法分类讨论法]如图,Rt△ABC中,∠B=90°,∠A=60°,P是边BC上一动点,过点C作射线CD⊥BC,Q是射线CD上一动点,连接PQ交AC于点E,在点P,Q的运动过程中,当△ABC与△PCQ全等时,∠AEQ的度数为 .
(第18题)
三、解答题(19~21题每题10分,其余每题12分,共66分)
19.[2023·益阳]如图,AB∥CD,直线MN与AB,CD分别交于点E,F,CD上有一点G且GE=GF,∠1=122°,求∠2的度数.
20.如图,已知A,D,C,E在同一直线上,BC和DF相交于点O,AD=CE,AB∥DF,AB=DF.
(1)求证:△ABC≌△DFE;
(2)连接CF,若∠BCF=54°,∠DFC=20°,求∠DFE的度数.
21.[2023·武汉]如图,在四边形ABCD中,AD∥BC,∠B=∠D,点E在BA的延长线上,连接CE.
(1)求证:∠E=∠ECD;
(2)若∠E=60°,CE平分∠BCD,直接写出△BCE的形状.
22.如图,已知点E,C在线段BF上,且BE=CF,CM∥DF.
(1)作图:在BC上方作射线BN,使∠CBN=∠1,交CM的延长线于点A(用尺规作图,保留作图痕迹,不写作法);
(2)在(1)的条件下,求证:AC=DF.
23.[2023·泰州新视角·条件选择题]如图,CD是五边形ABCDE的一边,若AM垂直平分CD,垂足为M,且 , ,则 .
给出下列信息:①AM平分∠BAE;②AB=AE;③BC=DE.请从中选择适当信息,将对应的序号填到横线上方,使之构成真命题,补全图形,并加以证明.
24.[新视角新定义型题]过三角形的顶点作射线与其对边相交,将三角形分成两个三角形.若得到的两个三角形中有等腰三角形,这条射线就叫作原三角形的“友好分割线”.
(1)下列三角形中,不存在“友好分割线”的是 (填序号).
①等腰直角三角形;②等边三角形;③顶角为150°的等腰三角形.
(2)如图①,在△ABC中,∠A=60°,∠B=40°,直接写出△ABC被“友好分割线”分得的等腰三角形顶角的度数.
(3)如图②,在△ABC中,∠A=30°,CD为AB边上的高,BD=2,E为AD的中点,过点E作直线l交AC于点F,作CM⊥l,DN⊥l,垂足为点M,N.若射线CD为△ABC的“友好分割线”,求CM+DN的最大值(提示:在直角三角形中,30°角所对的直角边等于斜边的一半).
答案
一、1. D 2. C 3. B
4. B 【点拨】逐一分析.两个锐角之和不一定是钝角,例如30°+30°=60°,故A不是真命题,不符合题意;三角形的任意两边之和大于第三边,故B是真命题,符合题意;“内错角相等”是假命题,“两直线平行,内错角相等”才是真命题,故C不符合题意;三角形三边中线的交点是三角形的重心,故D不是真命题,不符合题意.
5. A 6. D 7. C 8. C
9. B 【点拨】如图,连接AA',易知DA=DA',EA=EA',
∴∠DAA'=∠DA'A,∠EAA'=∠EA'A,
∴∠1=∠DAA'+∠DA'A=2∠DAA',
∠2=∠EAA'+∠EA'A=2∠EAA'.
∴∠1+∠2=2(∠DAA'+∠EAA')=2∠BAC.
10. C 【点拨】∵∠EAB=∠CAD,
∴∠EAB+∠BAD=∠CAD+∠BAD,即∠EAD=∠BAC.
∵∠ADB=∠ADE+∠EDB=∠DAC+∠C,∠EDB=∠DAC,
∴∠ADE=∠C.
在△AED和△ABC中,
∴△AED≌△ABC(ASA).
∴AE=AB,∠E=∠B,DE=BC.
故选C.
二、11.三角形具有稳定性 12.直角
13. AB=CD(答案不唯一) 14.10
15.假 【点拨】命题“若a>0,b>0,则a+b>0”的逆命题是“若a+b>0,则a>0,b>0”,该命题是假命题,可以用特殊值验证,如a=2,b=-1.
16.50 【点拨】∵AB=AC,AD=AE,
∴∠B=∠C,∠ADE=∠AED.
∵∠ADC=∠B+∠BAD,
∴∠ADE=∠ADC-∠EDC=∠B+∠BAD-∠EDC.
又∵∠AED=∠EDC+∠C,
∴∠B+∠BAD-∠EDC=∠EDC+∠C,
∴∠BAD=2∠EDC.
又∵∠EDC=25°,
∴∠BAD=2×25°=50°.
17.40° 【点拨】依题意,得∠EDO=∠CDB=20°,∠AEF=∠DEO.∵∠AOB=120°,∴∠OED=180°-∠EDO-∠AOB=40°.
∴∠AEF=∠DEO=40°.
18.90°或120° 【点拨】∵Rt△ABC中,∠B=90°,∠A=60°,∴∠ACB=30°.
∵CD⊥BC,∴∠PCQ=90°=∠B.
∴∠ACD=60°.
∵∠AEQ是△ECQ的外角,
∴∠AEQ=∠ACD+∠PQC.
当△ABC≌△PCQ时,∠PQC=∠ACB=30°,
∴∠AEQ=∠ACD+∠PQC=90°;
当△ABC≌△QCP时,∠PQC=∠A=60°,
∴∠AEQ=∠ACD+∠PQC=120°.
三、19.【解】∵AB∥CD,∠1=122°,
∴∠DFE=∠1=122°.
∴∠EFG=180°-∠DFE=58°.
又∵GE=GF,
∴∠FEG=∠EFG=58°.
∴∠2=180°-∠FEG-∠EFG=64°.
20.(1)【证明】∵AB∥DF,
∴∠A=∠EDF.
∵AD=CE,
∴AD+CD=CE+CD,即AC=DE.
在△ABC和△DFE中,
∴△ABC≌△DFE(SAS).
(2)【解】∵∠BCF=54°,∠DFC=20°,
∴∠DOC=∠BCF+∠DFC=54°+20°=74°.
又∵AB∥DF,∴∠B=∠DOC=74°.
又∵△ABC≌△DFE,∴∠DFE=∠B=74°.
21.(1)【证明】∵AD∥BC,∴∠EAD=∠B.
又∵∠B=∠D,∴∠EAD=∠D.
∴BE∥CD.∴∠E=∠ECD.
(2)【解】△BCE是等边三角形. 【点拨】∵∠E=60°,∠E=∠ECD,
∴∠ECD=60°.
又∵CE平分∠BCD,
∴∠BCE=∠ECD=60°.
∴∠B=180°-∠BCE-∠E=60°.
∴△BCE是等边三角形.
22.(1)【解】如图所示.
(2)【证明】∵CM∥DF,
∴∠MCE=∠F.
∵BE=CF,
∴BE+CE=CF+CE,即BC=EF.
在△ABC和△DEF中,
∴△ABC≌△DEF(ASA).∴AC=DF.
23.【解】②;③;①
证明:根据题意补全图形,如图所示.
连接AC,AD.∵AM垂直平分CD,
∴CM=DM,AC=AD.
又∵AM=AM,∴△ACM≌△ADM(SSS).
∴∠CAM=∠DAM.
在△ABC和△AED中,
∴△ABC≌△AED(SSS).
∴∠BAC=∠EAD.
又∵∠CAM=∠DAM,
∴∠BAC+∠CAM=∠EAD+∠DAM,
即∠BAM=∠EAM=∠BAE.
∴AM平分∠BAE.(答案不唯一)
24.【解】(1)② 【点拨】如图①,根据“友好分割线”的定义可知,等腰直角三角形和顶角为150°的等腰三角形存在“友好分割线”,等边三角形不存在“友好分割线”.
(2)△ABC被“友好分割线”分得的等腰三角形的顶角的度数为20°或40°或60°或80°或100°.
(3)如图②,作AG⊥l于点G,则∠AGE=90°.
∵射线CD为△ABC的“友好分割线”,
∴△CDB和△CDA中至少有一个是等腰三角形.
∵CD为AB边上的高,
∴∠CDB=∠CDA=90°.
∴∠ACD=90°-∠A=60°.
∴△CDA不是等腰三角形.
∴△CDB是等腰三角形.
∴CD=BD=2.
∵∠BAC=30°,∠ADC=90°,
∴AC=2CD=4.
∵DN⊥l于点N,
∴∠DNE=90°=∠AGE.
∵点E为AD的中点,∴DE=AE.
在△DNE和△AGE中,
∴△DNE≌△AGE(AAS).
∴DN=AG.
易知CM≤CF,AG≤AF,
∴CM+AG≤CF+AF,即CM+AG≤AC.
∴CM+DN≤4.
∴CM+DN的最大值为4.
一、选择题(每题3分,共30分)
1.[2023·衡阳母题·教材P44练习T2]下列长度的各组线段能组成一个三角形的是( )
A.1 cm,2 cm,3 cm B.3 cm,8 cm,5 cm
C.4 cm,5 cm,10 cm D.4 cm,5 cm,6 cm
2.[2023·宿迁]若等腰三角形有一个内角为110°,则这个等腰三角形的底角是( )
A.70° B.45° C.35° D.50°
3.[2023·青岛]如图,直线a∥b,∠1=63°,∠B=45°,则∠2的度数为( )
(第3题)
A.105° B.108° C.117° D.135°
4.[母题教材P59习题T3] 下列命题是真命题的是( )
A.两个锐角之和一定是钝角
B.三角形的任意两边之和大于第三边
C.内错角相等
D.三角形的重心是这个三角形的三条角平分线的交点
5.[2024·湖南师范大学附中月考]如图,在等边三角形ABC中,AD⊥BC,垂足为D,点E在线段AD上,∠EBC=45°,则∠ACE等于( )
(第5题)
A.15° B.30° C.45° D.60°
6.根据下列已知条件,能画出唯一的△ABC的是( )
A. AB=3,BC=4,AC=7 B. AB=4,BC=3,∠A=30°
C.∠A=∠B,AB=6 D.∠A=60°,∠B=45°,AC=4
7.[2023·盐城]小华将一副三角板(∠C=∠D=90°,∠B=30°,∠E=45°)按如图所示的方式摆放,其中AB∥EF,则∠1的度数为( )
(第7题)
A.45° B.60° C.75° D.105°
8.如图,在△ABC中,AD是BC边上的中线,CE是AB边上的高,若AB=4,S△ABD=6,则CE的长是( )
(第8题)
A.3 B.4 C.6 D.8
9.如图,将△ABC沿DE折叠,使点A落在A'处,则∠1+∠2与∠A的关系是( )
(第9题)
A.∠1+∠2=∠A B.∠1+∠2=2∠A
C.2(∠1+∠2)=3∠A D.∠1+∠2=
10.如图,D是△ABC的边BC上一点,DE交AB于点F,连接AE,AD,已知AD=AC,∠EAB=∠CAD=∠BDE,下列结论不一定正确的是( )
(第10题)
A. AB=AE B.∠B=∠E C.∠B=∠DAF D. DE=BC
二、填空题(每题3分,共24分)
11.[情境题生活应用] 如图,钢架桥的设计中采用了三角形的结构,其数学道理是 .
(第11题)
12.[2023·遂宁]若三角形三个内角的比为1∶2∶3,则这个三角形是 三角形.
13.[母题教材P86习题T2]如图,AB∥CD,AD与BC交于点O,请添加一个条件: ,使△AOB≌△DOC(只填一个条件即可).
(第13题)
14.[2024·岳阳十八中月考]如图,在△ABC中,按以下步骤作图:①分别以点B和C为圆心,以大于BC的长为半径作弧,两弧相交于点M和N;②作直线MN交AC于点D,连接BD.若AC=6,AB=4,则△ABD的周长为 .
(第14题)
15.命题“若a>0,b>0,则a+b>0”的逆命题是 (填“真”或“假” )命题.
16.如图,在△ABC中,AB=AC,AD=AE.若∠B=55°,∠EDC=25°,则∠BAD= °.
(第16题)
17.[新趋势学科综合]如图,一束光沿CD方向,先后经过平面镜OB,OA反射后,沿EF方向射出,已知∠AOB=120°,∠CDB=20°,则∠AEF= .
(第17题)
18.[新考法分类讨论法]如图,Rt△ABC中,∠B=90°,∠A=60°,P是边BC上一动点,过点C作射线CD⊥BC,Q是射线CD上一动点,连接PQ交AC于点E,在点P,Q的运动过程中,当△ABC与△PCQ全等时,∠AEQ的度数为 .
(第18题)
三、解答题(19~21题每题10分,其余每题12分,共66分)
19.[2023·益阳]如图,AB∥CD,直线MN与AB,CD分别交于点E,F,CD上有一点G且GE=GF,∠1=122°,求∠2的度数.
20.如图,已知A,D,C,E在同一直线上,BC和DF相交于点O,AD=CE,AB∥DF,AB=DF.
(1)求证:△ABC≌△DFE;
(2)连接CF,若∠BCF=54°,∠DFC=20°,求∠DFE的度数.
21.[2023·武汉]如图,在四边形ABCD中,AD∥BC,∠B=∠D,点E在BA的延长线上,连接CE.
(1)求证:∠E=∠ECD;
(2)若∠E=60°,CE平分∠BCD,直接写出△BCE的形状.
22.如图,已知点E,C在线段BF上,且BE=CF,CM∥DF.
(1)作图:在BC上方作射线BN,使∠CBN=∠1,交CM的延长线于点A(用尺规作图,保留作图痕迹,不写作法);
(2)在(1)的条件下,求证:AC=DF.
23.[2023·泰州新视角·条件选择题]如图,CD是五边形ABCDE的一边,若AM垂直平分CD,垂足为M,且 , ,则 .
给出下列信息:①AM平分∠BAE;②AB=AE;③BC=DE.请从中选择适当信息,将对应的序号填到横线上方,使之构成真命题,补全图形,并加以证明.
24.[新视角新定义型题]过三角形的顶点作射线与其对边相交,将三角形分成两个三角形.若得到的两个三角形中有等腰三角形,这条射线就叫作原三角形的“友好分割线”.
(1)下列三角形中,不存在“友好分割线”的是 (填序号).
①等腰直角三角形;②等边三角形;③顶角为150°的等腰三角形.
(2)如图①,在△ABC中,∠A=60°,∠B=40°,直接写出△ABC被“友好分割线”分得的等腰三角形顶角的度数.
(3)如图②,在△ABC中,∠A=30°,CD为AB边上的高,BD=2,E为AD的中点,过点E作直线l交AC于点F,作CM⊥l,DN⊥l,垂足为点M,N.若射线CD为△ABC的“友好分割线”,求CM+DN的最大值(提示:在直角三角形中,30°角所对的直角边等于斜边的一半).
答案
一、1. D 2. C 3. B
4. B 【点拨】逐一分析.两个锐角之和不一定是钝角,例如30°+30°=60°,故A不是真命题,不符合题意;三角形的任意两边之和大于第三边,故B是真命题,符合题意;“内错角相等”是假命题,“两直线平行,内错角相等”才是真命题,故C不符合题意;三角形三边中线的交点是三角形的重心,故D不是真命题,不符合题意.
5. A 6. D 7. C 8. C
9. B 【点拨】如图,连接AA',易知DA=DA',EA=EA',
∴∠DAA'=∠DA'A,∠EAA'=∠EA'A,
∴∠1=∠DAA'+∠DA'A=2∠DAA',
∠2=∠EAA'+∠EA'A=2∠EAA'.
∴∠1+∠2=2(∠DAA'+∠EAA')=2∠BAC.
10. C 【点拨】∵∠EAB=∠CAD,
∴∠EAB+∠BAD=∠CAD+∠BAD,即∠EAD=∠BAC.
∵∠ADB=∠ADE+∠EDB=∠DAC+∠C,∠EDB=∠DAC,
∴∠ADE=∠C.
在△AED和△ABC中,
∴△AED≌△ABC(ASA).
∴AE=AB,∠E=∠B,DE=BC.
故选C.
二、11.三角形具有稳定性 12.直角
13. AB=CD(答案不唯一) 14.10
15.假 【点拨】命题“若a>0,b>0,则a+b>0”的逆命题是“若a+b>0,则a>0,b>0”,该命题是假命题,可以用特殊值验证,如a=2,b=-1.
16.50 【点拨】∵AB=AC,AD=AE,
∴∠B=∠C,∠ADE=∠AED.
∵∠ADC=∠B+∠BAD,
∴∠ADE=∠ADC-∠EDC=∠B+∠BAD-∠EDC.
又∵∠AED=∠EDC+∠C,
∴∠B+∠BAD-∠EDC=∠EDC+∠C,
∴∠BAD=2∠EDC.
又∵∠EDC=25°,
∴∠BAD=2×25°=50°.
17.40° 【点拨】依题意,得∠EDO=∠CDB=20°,∠AEF=∠DEO.∵∠AOB=120°,∴∠OED=180°-∠EDO-∠AOB=40°.
∴∠AEF=∠DEO=40°.
18.90°或120° 【点拨】∵Rt△ABC中,∠B=90°,∠A=60°,∴∠ACB=30°.
∵CD⊥BC,∴∠PCQ=90°=∠B.
∴∠ACD=60°.
∵∠AEQ是△ECQ的外角,
∴∠AEQ=∠ACD+∠PQC.
当△ABC≌△PCQ时,∠PQC=∠ACB=30°,
∴∠AEQ=∠ACD+∠PQC=90°;
当△ABC≌△QCP时,∠PQC=∠A=60°,
∴∠AEQ=∠ACD+∠PQC=120°.
三、19.【解】∵AB∥CD,∠1=122°,
∴∠DFE=∠1=122°.
∴∠EFG=180°-∠DFE=58°.
又∵GE=GF,
∴∠FEG=∠EFG=58°.
∴∠2=180°-∠FEG-∠EFG=64°.
20.(1)【证明】∵AB∥DF,
∴∠A=∠EDF.
∵AD=CE,
∴AD+CD=CE+CD,即AC=DE.
在△ABC和△DFE中,
∴△ABC≌△DFE(SAS).
(2)【解】∵∠BCF=54°,∠DFC=20°,
∴∠DOC=∠BCF+∠DFC=54°+20°=74°.
又∵AB∥DF,∴∠B=∠DOC=74°.
又∵△ABC≌△DFE,∴∠DFE=∠B=74°.
21.(1)【证明】∵AD∥BC,∴∠EAD=∠B.
又∵∠B=∠D,∴∠EAD=∠D.
∴BE∥CD.∴∠E=∠ECD.
(2)【解】△BCE是等边三角形. 【点拨】∵∠E=60°,∠E=∠ECD,
∴∠ECD=60°.
又∵CE平分∠BCD,
∴∠BCE=∠ECD=60°.
∴∠B=180°-∠BCE-∠E=60°.
∴△BCE是等边三角形.
22.(1)【解】如图所示.
(2)【证明】∵CM∥DF,
∴∠MCE=∠F.
∵BE=CF,
∴BE+CE=CF+CE,即BC=EF.
在△ABC和△DEF中,
∴△ABC≌△DEF(ASA).∴AC=DF.
23.【解】②;③;①
证明:根据题意补全图形,如图所示.
连接AC,AD.∵AM垂直平分CD,
∴CM=DM,AC=AD.
又∵AM=AM,∴△ACM≌△ADM(SSS).
∴∠CAM=∠DAM.
在△ABC和△AED中,
∴△ABC≌△AED(SSS).
∴∠BAC=∠EAD.
又∵∠CAM=∠DAM,
∴∠BAC+∠CAM=∠EAD+∠DAM,
即∠BAM=∠EAM=∠BAE.
∴AM平分∠BAE.(答案不唯一)
24.【解】(1)② 【点拨】如图①,根据“友好分割线”的定义可知,等腰直角三角形和顶角为150°的等腰三角形存在“友好分割线”,等边三角形不存在“友好分割线”.
(2)△ABC被“友好分割线”分得的等腰三角形的顶角的度数为20°或40°或60°或80°或100°.
(3)如图②,作AG⊥l于点G,则∠AGE=90°.
∵射线CD为△ABC的“友好分割线”,
∴△CDB和△CDA中至少有一个是等腰三角形.
∵CD为AB边上的高,
∴∠CDB=∠CDA=90°.
∴∠ACD=90°-∠A=60°.
∴△CDA不是等腰三角形.
∴△CDB是等腰三角形.
∴CD=BD=2.
∵∠BAC=30°,∠ADC=90°,
∴AC=2CD=4.
∵DN⊥l于点N,
∴∠DNE=90°=∠AGE.
∵点E为AD的中点,∴DE=AE.
在△DNE和△AGE中,
∴△DNE≌△AGE(AAS).
∴DN=AG.
易知CM≤CF,AG≤AF,
∴CM+AG≤CF+AF,即CM+AG≤AC.
∴CM+DN≤4.
∴CM+DN的最大值为4.
同课章节目录
