第二章 直角三角形的边角关系 1 锐角三角函数 第1课时 正切(含答案)
文档属性
| 名称 | 第二章 直角三角形的边角关系 1 锐角三角函数 第1课时 正切(含答案) | 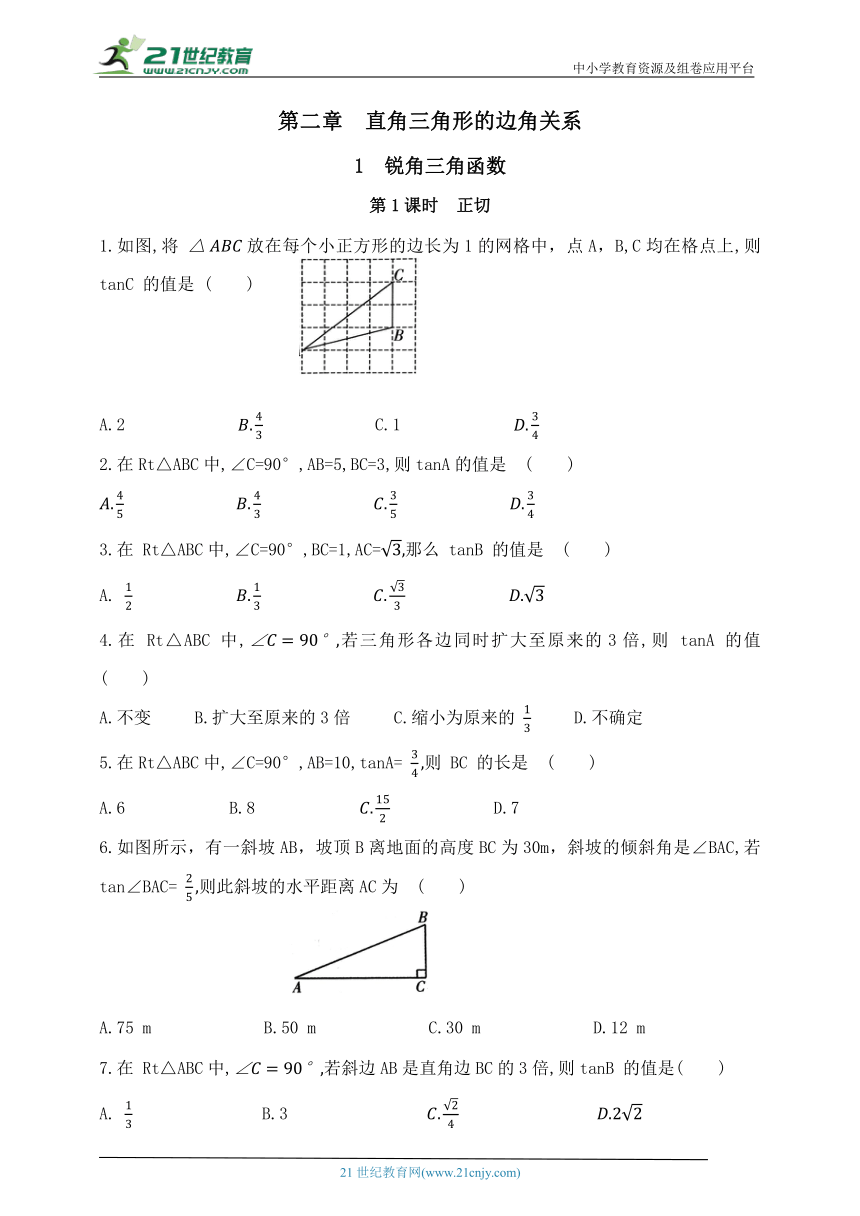 | |
| 格式 | docx | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-26 18:20:33 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第二章 直角三角形的边角关系
1 锐角三角函数
第1课时 正切
1.如图,将 放在每个小正方形的边长为1的网格中,点A,B,C均在格点上,则 tanC 的值是 ( )
A.2 C.1
2.在Rt△ABC中,∠C=90°,AB=5,BC=3,则tanA的值是 ( )
3.在 Rt△ABC中,∠C=90°,BC=1,AC=那么 tanB 的值是 ( )
A.
4.在 Rt△ABC 中,若三角形各边同时扩大至原来的3倍,则 tanA 的值( )
A.不变 B.扩大至原来的3倍 C.缩小为原来的 D.不确定
5.在Rt△ABC中,∠C=90°,AB=10,tanA= 则 BC 的长是 ( )
A.6 B.8 D.7
6.如图所示,有一斜坡AB,坡顶B离地面的高度BC为30m,斜坡的倾斜角是∠BAC,若tan∠BAC= 则此斜坡的水平距离AC为 ( )
A.75 m B.50 m C.30 m D.12 m
7.在 Rt△ABC中,若斜边AB是直角边BC的3倍,则tanB 的值是( )
A. B.3
8.如图,大坝的横截面是梯形ABCD,AD∥BC,坝顶宽 AD=4m ,坝高 AE=6m ,斜坡AB 的坡度 斜坡 DC 的坡角∠C=45°,那么坝底 BC的长度是 ( )
第8题图 第9题图
9.如图,在平地上种植树木时,要求株距(相邻两棵树之间的水平距离)为10m,若在坡度为1: 1.25 的山坡上种树,也要求株距为10m,那么相邻两棵树间的坡面距离为( )
10.已知在 Rt△ABC 中,∠C=90°, 则 BC的长为____________.
11.已知正方形ABCD的边长为2,点P是直线CD上一点,若连接BP,则的值是____________.
12.在 中, 若 则
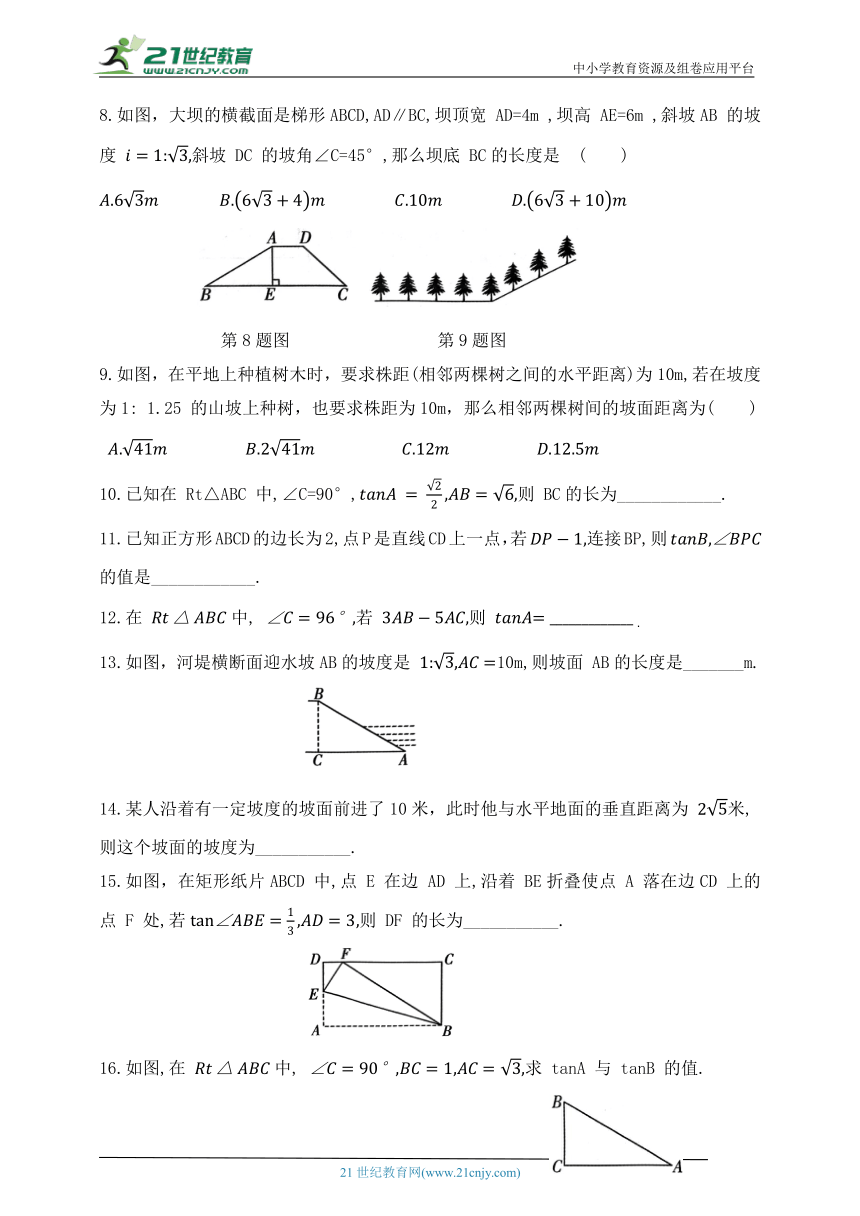
13.如图,河堤横断面迎水坡AB的坡度是 10m,则坡面 AB的长度是_______m.
14.某人沿着有一定坡度的坡面前进了10米,此时他与水平地面的垂直距离为 米,
则这个坡面的坡度为___________.
15.如图,在矩形纸片ABCD 中,点 E 在边 AD 上,沿着 BE折叠使点 A 落在边CD 上的点 F 处,若则 DF 的长为___________.
16.如图,在 中, 求 tanA 与 tanB 的值.
17.如图,在边长相同的小正方形网格中,点 A,B,C,D都在这些小正方形的顶点上,线段 AB 与CD 相交于点 P,则 的值为___________.
第 17题图 第 18题图
18.如图,将以 A 为直角顶点的等腰直角三角形ABC 沿直线 BC平移得到 使点 与C 重合,连接 则 的值为____________.
19.在矩形 ABCD中, 点 E 为AD 边上一点,沿CE将 对折,使点 D 正好落在AB 边上,求
参考答案
1. B 2. D 3. D 4. A 5. A 6. A
7. D 解析:设 则
由勾股定理,得
8. D 9. B
11.2 或 解析:此题有两种
可能:
①如图1,当点 P在线段CD上,
2-1=1,
②如图2,当点 P 在CD 的延长线上,
1=3,
14.1:2
15.1 解析:由折叠,得
∵∠EFB=∠C=∠D=90°,∴∠DFE+∠DEF=90°,∠DFE+∠BFC=90°,
∴∠DEF=∠BFC,∴△DEF∽△CFB,
∵BC=AD=3,∴DF=1.
16.解:∵∠C=90°,
17.2
19.解:∵∠AFE+∠EFC+∠BFC=180°,
又由折叠,得∠EFC=∠EDC=90°,CF=CD,∴∠AFE+∠BFC=90°.
又∵在 Rt△BCF 中,∠BCF+∠BFC=90°,∴∠AFE=∠BCF.
在 Rt△BFC中,BC=8,CF=CD=10,由勾股定理,得
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第二章 直角三角形的边角关系
1 锐角三角函数
第1课时 正切
1.如图,将 放在每个小正方形的边长为1的网格中,点A,B,C均在格点上,则 tanC 的值是 ( )
A.2 C.1
2.在Rt△ABC中,∠C=90°,AB=5,BC=3,则tanA的值是 ( )
3.在 Rt△ABC中,∠C=90°,BC=1,AC=那么 tanB 的值是 ( )
A.
4.在 Rt△ABC 中,若三角形各边同时扩大至原来的3倍,则 tanA 的值( )
A.不变 B.扩大至原来的3倍 C.缩小为原来的 D.不确定
5.在Rt△ABC中,∠C=90°,AB=10,tanA= 则 BC 的长是 ( )
A.6 B.8 D.7
6.如图所示,有一斜坡AB,坡顶B离地面的高度BC为30m,斜坡的倾斜角是∠BAC,若tan∠BAC= 则此斜坡的水平距离AC为 ( )
A.75 m B.50 m C.30 m D.12 m
7.在 Rt△ABC中,若斜边AB是直角边BC的3倍,则tanB 的值是( )
A. B.3
8.如图,大坝的横截面是梯形ABCD,AD∥BC,坝顶宽 AD=4m ,坝高 AE=6m ,斜坡AB 的坡度 斜坡 DC 的坡角∠C=45°,那么坝底 BC的长度是 ( )
第8题图 第9题图
9.如图,在平地上种植树木时,要求株距(相邻两棵树之间的水平距离)为10m,若在坡度为1: 1.25 的山坡上种树,也要求株距为10m,那么相邻两棵树间的坡面距离为( )
10.已知在 Rt△ABC 中,∠C=90°, 则 BC的长为____________.
11.已知正方形ABCD的边长为2,点P是直线CD上一点,若连接BP,则的值是____________.
12.在 中, 若 则
13.如图,河堤横断面迎水坡AB的坡度是 10m,则坡面 AB的长度是_______m.
14.某人沿着有一定坡度的坡面前进了10米,此时他与水平地面的垂直距离为 米,
则这个坡面的坡度为___________.
15.如图,在矩形纸片ABCD 中,点 E 在边 AD 上,沿着 BE折叠使点 A 落在边CD 上的点 F 处,若则 DF 的长为___________.
16.如图,在 中, 求 tanA 与 tanB 的值.
17.如图,在边长相同的小正方形网格中,点 A,B,C,D都在这些小正方形的顶点上,线段 AB 与CD 相交于点 P,则 的值为___________.
第 17题图 第 18题图
18.如图,将以 A 为直角顶点的等腰直角三角形ABC 沿直线 BC平移得到 使点 与C 重合,连接 则 的值为____________.
19.在矩形 ABCD中, 点 E 为AD 边上一点,沿CE将 对折,使点 D 正好落在AB 边上,求
参考答案
1. B 2. D 3. D 4. A 5. A 6. A
7. D 解析:设 则
由勾股定理,得
8. D 9. B
11.2 或 解析:此题有两种
可能:
①如图1,当点 P在线段CD上,
2-1=1,
②如图2,当点 P 在CD 的延长线上,
1=3,
14.1:2
15.1 解析:由折叠,得
∵∠EFB=∠C=∠D=90°,∴∠DFE+∠DEF=90°,∠DFE+∠BFC=90°,
∴∠DEF=∠BFC,∴△DEF∽△CFB,
∵BC=AD=3,∴DF=1.
16.解:∵∠C=90°,
17.2
19.解:∵∠AFE+∠EFC+∠BFC=180°,
又由折叠,得∠EFC=∠EDC=90°,CF=CD,∴∠AFE+∠BFC=90°.
又∵在 Rt△BCF 中,∠BCF+∠BFC=90°,∴∠AFE=∠BCF.
在 Rt△BFC中,BC=8,CF=CD=10,由勾股定理,得
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
