第二章 直角三角形的边角关系 1 锐角三角函数 第2课时 正弦和余弦(含答案)
文档属性
| 名称 | 第二章 直角三角形的边角关系 1 锐角三角函数 第2课时 正弦和余弦(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 5.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-26 18:24:30 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第二章 三角形的边角关系
1 锐角三角函数
第2课时 正弦和余弦
1.已知在 中, 则 ( )
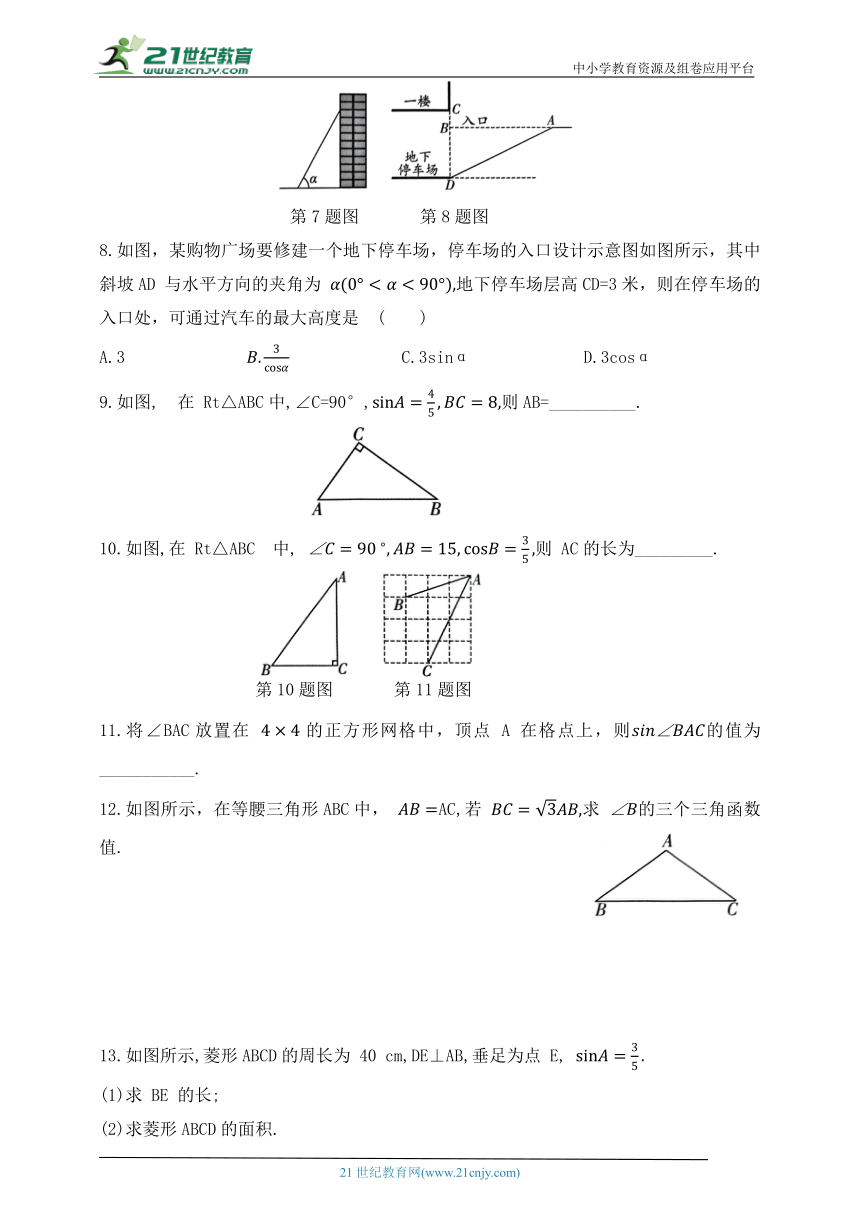
2.如图,在下列网格中,小正方形的边长均为1,点 A,B,O都在格点上,则 的正弦值是 ( )
3.已知∠A+∠B=90°,且则 tanB 的值为 ( )
4.在△ABC中,∠C=90°,且c=3b,则cosA=( )
5.如图,在 Rt△ABC 中,CD是斜边 AB 上的高,∠A≠45°,则下列比值中不等于sinA 的是( )
6.已知 则锐角α的取值范围是 ( )
7.如图,梯子跟地面的夹角为 ,关于∠α的三角函数值与梯子的倾斜程度之间的关系,下列叙述正确的是( )
A. sinα的值越小,梯子越陡 B.cosα的值越小,梯子越陡
C. tanα的值越小,梯子越陡 D.陡缓程度与∠α的三角函数值无关
第7题图 第8题图
8.如图,某购物广场要修建一个地下停车场,停车场的入口设计示意图如图所示,其中斜坡AD 与水平方向的夹角为 地下停车场层高CD=3米,则在停车场的入口处,可通过汽车的最大高度是 ( )
A.3 C.3sinα D.3cosα
9.如图, 在 Rt△ABC中,∠C=90°,则AB=__________.
10.如图,在 Rt△ABC 中, 则 AC的长为_________.
第10题图 第11题图
11.将∠BAC放置在 的正方形网格中,顶点 A 在格点上,则的值为___________.
12.如图所示,在等腰三角形ABC中, AC,若 求 的三个三角函数值.
13.如图所示,菱形ABCD的周长为 40 cm,DE⊥AB,垂足为点 E,
(1)求 BE 的长;
(2)求菱形ABCD的面积.
14.请阅读下面材料,并根据提供的解题思路求解问题:
如图1,在边长为1的正方形网格中,连接格点 D,N 和E,C,DN 和 EC 相交于点P,求 的值.
【解题思路】
要求一个锐角的三角函数值,我们往往需要找出(或构造出)一个直角三角形.观察发现,问题中的 不在直角三角形中,我们可以利用网格画平行线等方法解决此类问题,比如连接格点 M,N,可发现MN∥EC,则 连接DM,那么∠CPN 就变换到 Rt△DMN 中,进而求出答案.
【解决问题】
(1)请根据上述方法,求图1中的值;
(2)如图2,在边长为1 的正方形网格中,AN 与 CM 相交于点 P,求 sin∠CPN的值.
15.如图,在 Rt△ABC中, D 是边AB 的中点,BE⊥CD,垂足为点 E.已知
(1)求线段CD 的长;
(2)求 cos∠DBE 的值.
参考答案
1. A 2. D 3. C 4. C 5. D 6. B 7. B
8. D 解析:过点 C 作 垂足为点 E,
∵斜坡AD 与水平方向的夹角为α,
在 中, (米),
故在停车场的入口处,可通过汽车的最大高度是 3cosα米.
9.10 10.12
12.解:如图,过点 A作. 交 BC 于点 D.
又
由勾股定理,得
在 中,
13.解:(1)∵菱形 ABCD的周长为40 cm, ∴AD=AB=10 cm.
又
在 Rt△ADE中,由勾股定理,得
所以,BE的长为 2cm;
(2)菱形的面积
∴菱形ABCD 的面积为
14.解:(1)如图1所示,连接格点 M,N,D.
∵点M,N,D都在格点上,,
∥
是直角三角形.
在 中,
(2)如图2所示,连接格点 N,G,A.
∵点 N,G,A 在格点上,
∴△AGN是等腰直角三角形.
∵tan∠CMK=tan∠GAK=2,∴∠CMK=∠GAK.∴AG∥CM.∴∠CPN=∠GAN.
在 Rt△AGN中,
15.解:
∵△ABC为直角三角形,D是边AB 的中点,∴CD=5;
(2)∵AB=10,AC=6,
∵△ABC为直角三角形,点 D 是边AB的中点,∴DC=DB=5,
∴∠DCB=∠ABC,
∵BE⊥CD,∴∠BEC=90°,
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第二章 三角形的边角关系
1 锐角三角函数
第2课时 正弦和余弦
1.已知在 中, 则 ( )
2.如图,在下列网格中,小正方形的边长均为1,点 A,B,O都在格点上,则 的正弦值是 ( )
3.已知∠A+∠B=90°,且则 tanB 的值为 ( )
4.在△ABC中,∠C=90°,且c=3b,则cosA=( )
5.如图,在 Rt△ABC 中,CD是斜边 AB 上的高,∠A≠45°,则下列比值中不等于sinA 的是( )
6.已知 则锐角α的取值范围是 ( )
7.如图,梯子跟地面的夹角为 ,关于∠α的三角函数值与梯子的倾斜程度之间的关系,下列叙述正确的是( )
A. sinα的值越小,梯子越陡 B.cosα的值越小,梯子越陡
C. tanα的值越小,梯子越陡 D.陡缓程度与∠α的三角函数值无关
第7题图 第8题图
8.如图,某购物广场要修建一个地下停车场,停车场的入口设计示意图如图所示,其中斜坡AD 与水平方向的夹角为 地下停车场层高CD=3米,则在停车场的入口处,可通过汽车的最大高度是 ( )
A.3 C.3sinα D.3cosα
9.如图, 在 Rt△ABC中,∠C=90°,则AB=__________.
10.如图,在 Rt△ABC 中, 则 AC的长为_________.
第10题图 第11题图
11.将∠BAC放置在 的正方形网格中,顶点 A 在格点上,则的值为___________.
12.如图所示,在等腰三角形ABC中, AC,若 求 的三个三角函数值.
13.如图所示,菱形ABCD的周长为 40 cm,DE⊥AB,垂足为点 E,
(1)求 BE 的长;
(2)求菱形ABCD的面积.
14.请阅读下面材料,并根据提供的解题思路求解问题:
如图1,在边长为1的正方形网格中,连接格点 D,N 和E,C,DN 和 EC 相交于点P,求 的值.
【解题思路】
要求一个锐角的三角函数值,我们往往需要找出(或构造出)一个直角三角形.观察发现,问题中的 不在直角三角形中,我们可以利用网格画平行线等方法解决此类问题,比如连接格点 M,N,可发现MN∥EC,则 连接DM,那么∠CPN 就变换到 Rt△DMN 中,进而求出答案.
【解决问题】
(1)请根据上述方法,求图1中的值;
(2)如图2,在边长为1 的正方形网格中,AN 与 CM 相交于点 P,求 sin∠CPN的值.
15.如图,在 Rt△ABC中, D 是边AB 的中点,BE⊥CD,垂足为点 E.已知
(1)求线段CD 的长;
(2)求 cos∠DBE 的值.
参考答案
1. A 2. D 3. C 4. C 5. D 6. B 7. B
8. D 解析:过点 C 作 垂足为点 E,
∵斜坡AD 与水平方向的夹角为α,
在 中, (米),
故在停车场的入口处,可通过汽车的最大高度是 3cosα米.
9.10 10.12
12.解:如图,过点 A作. 交 BC 于点 D.
又
由勾股定理,得
在 中,
13.解:(1)∵菱形 ABCD的周长为40 cm, ∴AD=AB=10 cm.
又
在 Rt△ADE中,由勾股定理,得
所以,BE的长为 2cm;
(2)菱形的面积
∴菱形ABCD 的面积为
14.解:(1)如图1所示,连接格点 M,N,D.
∵点M,N,D都在格点上,,
∥
是直角三角形.
在 中,
(2)如图2所示,连接格点 N,G,A.
∵点 N,G,A 在格点上,
∴△AGN是等腰直角三角形.
∵tan∠CMK=tan∠GAK=2,∴∠CMK=∠GAK.∴AG∥CM.∴∠CPN=∠GAN.
在 Rt△AGN中,
15.解:
∵△ABC为直角三角形,D是边AB 的中点,∴CD=5;
(2)∵AB=10,AC=6,
∵△ABC为直角三角形,点 D 是边AB的中点,∴DC=DB=5,
∴∠DCB=∠ABC,
∵BE⊥CD,∴∠BEC=90°,
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
