3.5共点力的平衡(教学课件)——高中物理人教版(2019)必修第一册(共25张PPT)
文档属性
| 名称 | 3.5共点力的平衡(教学课件)——高中物理人教版(2019)必修第一册(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 23.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-07-26 19:56:16 | ||
图片预览






文档简介
(共30张PPT)
3.5 共点力的平衡
新课引入
平衡是一种美
问题
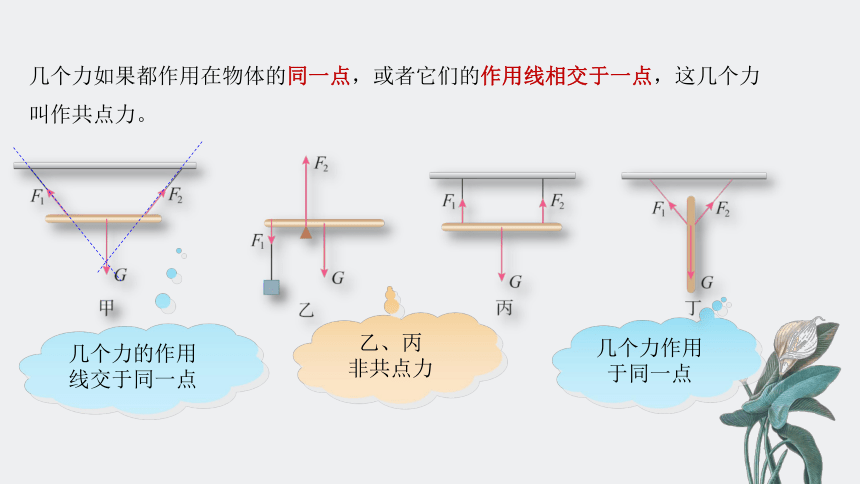
图甲、乙、丙、丁分别画出了重力为G 的木棒在力 F1 和 F2 的共同作用下处于平衡状态的情况,这些力都位于同一平面内。根据每幅图中各个力作用线的几何关系,可以把上述四种情况的受力分成两类,你认为哪些情况属于同一类?你是根据什么来划分的?
几个力作用于同一点
几个力的作用线交于同一点
几个力如果都作用在物体的同一点,或者它们的作用线相交于一点,这几个力叫作共点力。
乙、丙
非共点力
新课讲解
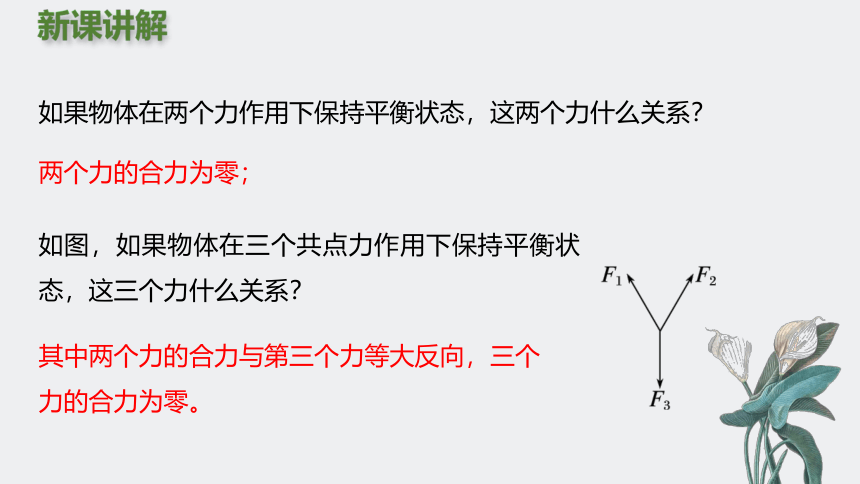
如果物体在两个力作用下保持平衡状态,这两个力什么关系?
两个力的合力为零;
如图,如果物体在三个共点力作用下保持平衡状态,这三个力什么关系?
其中两个力的合力与第三个力等大反向,三个力的合力为零。
新课讲解
静止的书
静止的电灯
随传送带匀速
运送的物体
沿直线公路匀速
前进的汽车
请在下图中画出各物体受力的示意图,并分析它们的运动状态有什么共同点?
平衡状态
共点力的平衡条件
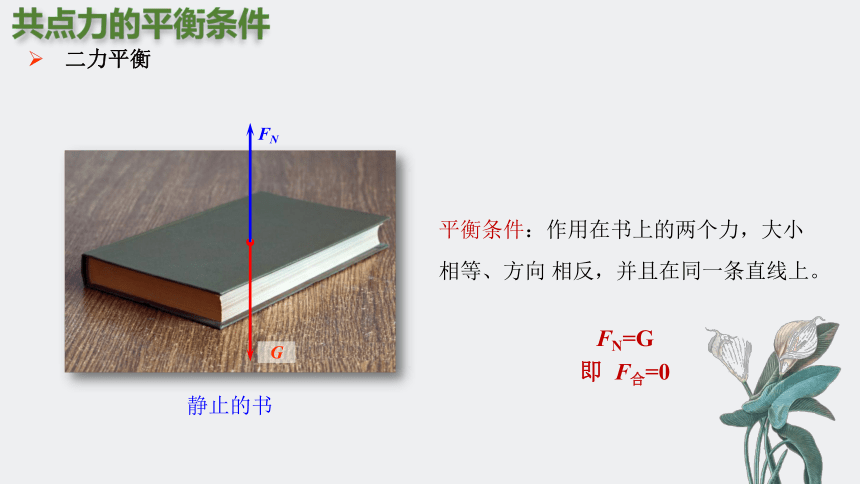
静止的书
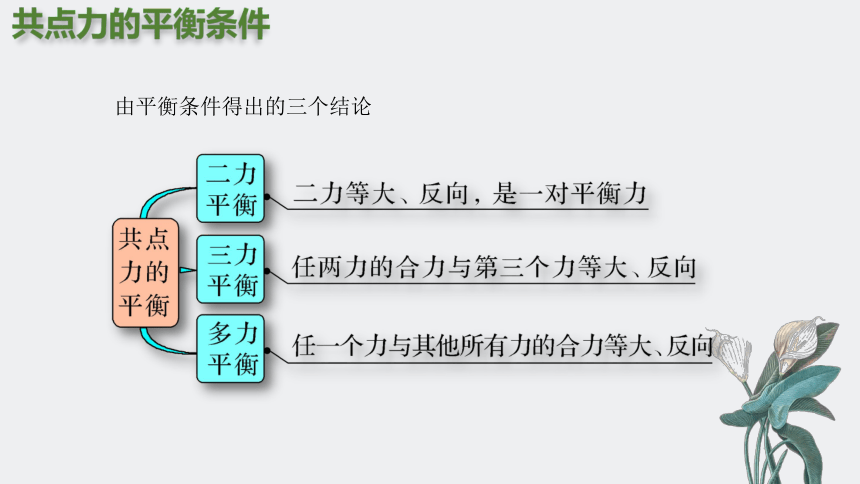
二力平衡
平衡条件:作用在书上的两个力,大小 相等、方向 相反,并且在同一条直线上。
FN=G
即 F合=0
G
FN
F
F
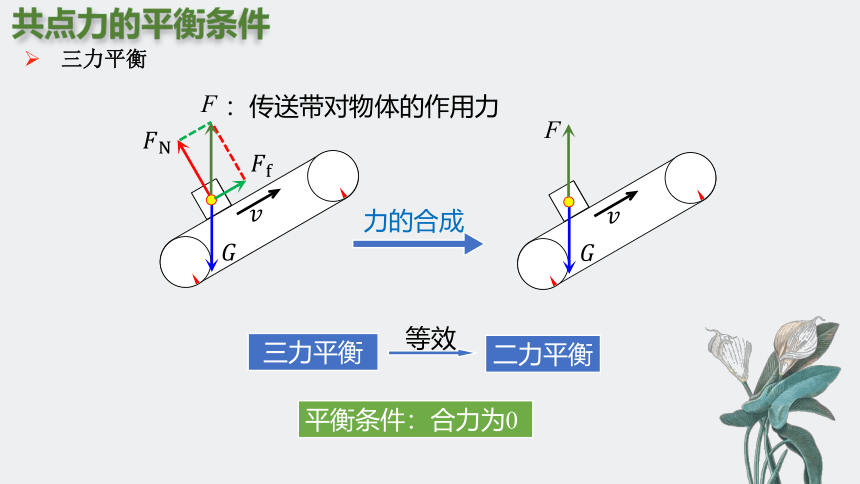
:传送带对物体的作用力
力的合成
平衡条件:合力为0
三力平衡
二力平衡
等效
三力平衡
共点力的平衡条件
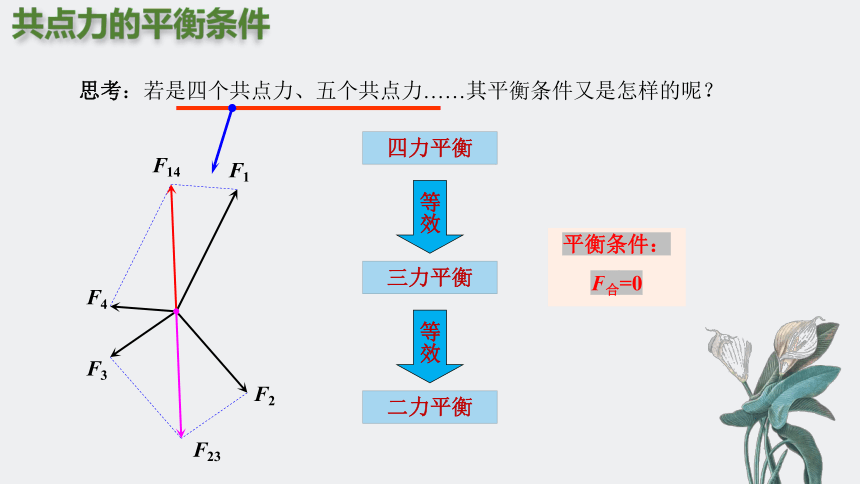
思考:若是四个共点力、五个共点力……其平衡条件又是怎样的呢?
F1
F2
F3
F4
F14
F23
四力平衡
三力平衡
二力平衡
等效
等效
平衡条件:
F合=0
共点力的平衡条件
共点力的平衡条件
共点力平衡的条件
在共点力作用下物体平衡的条件是合力为0。
由平衡条件得出的三个结论
共点力的平衡条件
方法总结
常用方法
合成法 物体在三个共点力作用下处于平衡状态时,任意两个力的合力与第三个力大小相等、方向相反
分解法 物体在三个共点力作用下处于平衡状态时,将某个力按作用效果分解,则其分力与其他两个力分别平衡
解题步骤
(1)明确研究对象(物体、质点或绳的结点等)。
(2)分析研究对象所处的运动状态,判定其是否处于平衡状态。
(3)对研究对象进行受力分析,并画出受力示意图。
(4)建立合适的坐标系,应用共点力平衡的条件,选择恰当的方法列出平衡方程。
(5)求解方程,并讨论结果。
方法总结
【例题】某幼儿园要在空地上做一个滑梯,根据空地的大小,滑梯的水平跨度确定为6m。设计时,滑板和儿童裤料之间的动摩擦因数取0.4,为使儿童在滑梯游戏时能在滑板上滑下,滑梯 要多高?
A
B
C
)θ
模型构建
至少
方法总结
方法一:正交分解法
Ff=μFN ③
把①②代入③式有
化简得:h = μb = 2.4m
解:以滑梯上正匀速下滑的小孩为研究对象,设BC高度为h,AC长度为b,斜面AB长度为l,倾角为θ。
沿平行和垂直于斜面两个方向建立直角坐标系,把重力G沿两个坐标轴方向分解为F1和F2。
Ff=F1=Gsinθ= ①
FN=F2=Gcosθ= ②
x轴
y轴
受力分析如下图所示,
分别列x轴和y轴的平衡状态方程。
A
B
C
θ
x
y
)θ
G
Ff
FN
F1
F2
θ
方法总结
将支持力和摩擦力根据平行四边形法合成为 F,根据平衡条件可知:F与重力G等大、反向、共线,即 F=G 。
方法二:合成法
FN
G
G’
A
B
C
)θ
θ
F
G
Ff
FN
Ff=μFN ③
把①②代入③式有
化简得:h = μb = 2.4m
Ff=Fsinθ=Gsinθ= ①
FN=Fcosθ=Gcosθ= ②
解:以滑梯上正匀速下滑的小孩为研究对象,设BC高度为h,AC长度为b,斜面AB长度为l,倾角为θ。
受力分析如下图所示,
θ
方法总结
平衡状态:
运动状态不再变化()
①静止( v=0)
②匀速直线运动( v0)
平衡条件:
F合=0
方法总结
方法总结
“活结”与“死结”、“活杆”与“死杆”
方法总结
动态平衡
控制某些物理量,使物体的状态发生缓慢变化,而在这个过程中物体又始终处于一系列的平衡状态。
人通过跨过定滑轮的轻绳牵引一物体,人向右缓慢移动。
经典例题
用绳AO、BO悬挂一个重物,BO水平,O为半圆形支架的圆心,悬点A和B在支架上。悬点A固定不动,将悬点B从图示位置逐渐移动到C点的过程中,分析绳OA和绳OB上的拉力的大小变化情况( )
A.绳OA的拉力不变 绳OB的拉力减小
B.绳OA的拉力逐渐减小 绳OB的拉力先减小后增大
C.绳OA的拉力不变 绳OB的拉力先减小后增大
D.绳OA的拉力逐渐减小 绳OB的拉力增大
将AO绳、BO绳的拉力合成,其合力与重力等大反向,逐渐改变OB绳拉力的方向,使FB与竖直方向的夹角变小,得到多个平行四边形,如图所示,由图可知FA逐渐减小,且方向不变,而FB先减小后增大,且方向不断改变,当FB与FA垂直时,FB最小。
经典例题
(多选)半圆柱体P放在粗糙的水平地面上,右端有固定放置的竖直挡板MN,在P和MN之间放有一个光滑均匀的小圆柱体Q,整个装置处于静止状态。如图所示,若用外力使MN保持竖直,缓慢地向右移动,在Q落到地面以前,发现P始终保持静止,在此过程中( )
A.MN对Q的弹力逐渐增大
B.地面对P的摩擦力逐渐增大
C.P、Q间的弹力先减小后增大
D.Q所受的合力逐渐增大
经典例题
P对Q的弹力为F,MN对Q的弹力为FN,挡板MN向右运动时,F和竖直方向的夹角逐渐增大,而小圆柱体所受重力大小不变,所以F和FN的合力大小不变;由图可知,F和FN都在不断增大;对P、Q整体受力分析知,地面对P的摩擦力大小就等于FN,所以地面对P的摩擦力也逐渐增大。
经典例题
方法总结
临界极值问题
固定斜面上的一物块受到一外力F的作用。物块在斜面上保持静止,F的最大值和最小值分别为F1和F2(F1和F2的方向均沿斜面向上)。求出物块与斜面间的最大静摩擦力?
方法总结
1.临界问题
(1)问题界定:物体所处平衡状态将要发生变化的状态为临界状态,涉及临界状态的问题为临界问题。
(2)问题特点
①当某物理量发生变化时,会引起其他几个物理量的变化。
②注意某现象“恰好出现”或“恰好不出现”的条件。
(3)处理方法:基本方法是假设推理法,即先假设某种情况成立,然后根据平衡条件及有关知识进行论证、求解。
方法总结
2.极值问题
(1)问题界定:物体平衡的极值问题,一般指在力的变化过程中涉及力的最大值和最小值的问题。
(2)处理方法
①解析法:根据物体的平衡条件列出方程,在解方程时,采用数学知识求极值或者根据物理临界条件求极值。
②图解法:根据物体的平衡条件作出力的矢量图,画出平行四边形或者矢量三角形进行动态分析,确定最大值或最小值。
如图所示,质量为m的物体置于倾角为θ的固定斜面上,物体与斜面之间的动摩擦因数为μ,先用平行于斜面的推力F1作用于物体上使其恰能沿斜面匀速上滑,若改用水平推力F2作用于物体上,也恰能使物体沿斜面匀速上滑,则两次的推力之比为F1/ F2( )
A.cos θ+μsin θ
B.cos θ-μsin θ
C.1+μtan θ
D.1-μtan θ
经典例题
经典例题
谢
谢
观
看
3.5 共点力的平衡
新课引入
平衡是一种美
问题
图甲、乙、丙、丁分别画出了重力为G 的木棒在力 F1 和 F2 的共同作用下处于平衡状态的情况,这些力都位于同一平面内。根据每幅图中各个力作用线的几何关系,可以把上述四种情况的受力分成两类,你认为哪些情况属于同一类?你是根据什么来划分的?
几个力作用于同一点
几个力的作用线交于同一点
几个力如果都作用在物体的同一点,或者它们的作用线相交于一点,这几个力叫作共点力。
乙、丙
非共点力
新课讲解
如果物体在两个力作用下保持平衡状态,这两个力什么关系?
两个力的合力为零;
如图,如果物体在三个共点力作用下保持平衡状态,这三个力什么关系?
其中两个力的合力与第三个力等大反向,三个力的合力为零。
新课讲解
静止的书
静止的电灯
随传送带匀速
运送的物体
沿直线公路匀速
前进的汽车
请在下图中画出各物体受力的示意图,并分析它们的运动状态有什么共同点?
平衡状态
共点力的平衡条件
静止的书
二力平衡
平衡条件:作用在书上的两个力,大小 相等、方向 相反,并且在同一条直线上。
FN=G
即 F合=0
G
FN
F
F
:传送带对物体的作用力
力的合成
平衡条件:合力为0
三力平衡
二力平衡
等效
三力平衡
共点力的平衡条件
思考:若是四个共点力、五个共点力……其平衡条件又是怎样的呢?
F1
F2
F3
F4
F14
F23
四力平衡
三力平衡
二力平衡
等效
等效
平衡条件:
F合=0
共点力的平衡条件
共点力的平衡条件
共点力平衡的条件
在共点力作用下物体平衡的条件是合力为0。
由平衡条件得出的三个结论
共点力的平衡条件
方法总结
常用方法
合成法 物体在三个共点力作用下处于平衡状态时,任意两个力的合力与第三个力大小相等、方向相反
分解法 物体在三个共点力作用下处于平衡状态时,将某个力按作用效果分解,则其分力与其他两个力分别平衡
解题步骤
(1)明确研究对象(物体、质点或绳的结点等)。
(2)分析研究对象所处的运动状态,判定其是否处于平衡状态。
(3)对研究对象进行受力分析,并画出受力示意图。
(4)建立合适的坐标系,应用共点力平衡的条件,选择恰当的方法列出平衡方程。
(5)求解方程,并讨论结果。
方法总结
【例题】某幼儿园要在空地上做一个滑梯,根据空地的大小,滑梯的水平跨度确定为6m。设计时,滑板和儿童裤料之间的动摩擦因数取0.4,为使儿童在滑梯游戏时能在滑板上滑下,滑梯 要多高?
A
B
C
)θ
模型构建
至少
方法总结
方法一:正交分解法
Ff=μFN ③
把①②代入③式有
化简得:h = μb = 2.4m
解:以滑梯上正匀速下滑的小孩为研究对象,设BC高度为h,AC长度为b,斜面AB长度为l,倾角为θ。
沿平行和垂直于斜面两个方向建立直角坐标系,把重力G沿两个坐标轴方向分解为F1和F2。
Ff=F1=Gsinθ= ①
FN=F2=Gcosθ= ②
x轴
y轴
受力分析如下图所示,
分别列x轴和y轴的平衡状态方程。
A
B
C
θ
x
y
)θ
G
Ff
FN
F1
F2
θ
方法总结
将支持力和摩擦力根据平行四边形法合成为 F,根据平衡条件可知:F与重力G等大、反向、共线,即 F=G 。
方法二:合成法
FN
G
G’
A
B
C
)θ
θ
F
G
Ff
FN
Ff=μFN ③
把①②代入③式有
化简得:h = μb = 2.4m
Ff=Fsinθ=Gsinθ= ①
FN=Fcosθ=Gcosθ= ②
解:以滑梯上正匀速下滑的小孩为研究对象,设BC高度为h,AC长度为b,斜面AB长度为l,倾角为θ。
受力分析如下图所示,
θ
方法总结
平衡状态:
运动状态不再变化()
①静止( v=0)
②匀速直线运动( v0)
平衡条件:
F合=0
方法总结
方法总结
“活结”与“死结”、“活杆”与“死杆”
方法总结
动态平衡
控制某些物理量,使物体的状态发生缓慢变化,而在这个过程中物体又始终处于一系列的平衡状态。
人通过跨过定滑轮的轻绳牵引一物体,人向右缓慢移动。
经典例题
用绳AO、BO悬挂一个重物,BO水平,O为半圆形支架的圆心,悬点A和B在支架上。悬点A固定不动,将悬点B从图示位置逐渐移动到C点的过程中,分析绳OA和绳OB上的拉力的大小变化情况( )
A.绳OA的拉力不变 绳OB的拉力减小
B.绳OA的拉力逐渐减小 绳OB的拉力先减小后增大
C.绳OA的拉力不变 绳OB的拉力先减小后增大
D.绳OA的拉力逐渐减小 绳OB的拉力增大
将AO绳、BO绳的拉力合成,其合力与重力等大反向,逐渐改变OB绳拉力的方向,使FB与竖直方向的夹角变小,得到多个平行四边形,如图所示,由图可知FA逐渐减小,且方向不变,而FB先减小后增大,且方向不断改变,当FB与FA垂直时,FB最小。
经典例题
(多选)半圆柱体P放在粗糙的水平地面上,右端有固定放置的竖直挡板MN,在P和MN之间放有一个光滑均匀的小圆柱体Q,整个装置处于静止状态。如图所示,若用外力使MN保持竖直,缓慢地向右移动,在Q落到地面以前,发现P始终保持静止,在此过程中( )
A.MN对Q的弹力逐渐增大
B.地面对P的摩擦力逐渐增大
C.P、Q间的弹力先减小后增大
D.Q所受的合力逐渐增大
经典例题
P对Q的弹力为F,MN对Q的弹力为FN,挡板MN向右运动时,F和竖直方向的夹角逐渐增大,而小圆柱体所受重力大小不变,所以F和FN的合力大小不变;由图可知,F和FN都在不断增大;对P、Q整体受力分析知,地面对P的摩擦力大小就等于FN,所以地面对P的摩擦力也逐渐增大。
经典例题
方法总结
临界极值问题
固定斜面上的一物块受到一外力F的作用。物块在斜面上保持静止,F的最大值和最小值分别为F1和F2(F1和F2的方向均沿斜面向上)。求出物块与斜面间的最大静摩擦力?
方法总结
1.临界问题
(1)问题界定:物体所处平衡状态将要发生变化的状态为临界状态,涉及临界状态的问题为临界问题。
(2)问题特点
①当某物理量发生变化时,会引起其他几个物理量的变化。
②注意某现象“恰好出现”或“恰好不出现”的条件。
(3)处理方法:基本方法是假设推理法,即先假设某种情况成立,然后根据平衡条件及有关知识进行论证、求解。
方法总结
2.极值问题
(1)问题界定:物体平衡的极值问题,一般指在力的变化过程中涉及力的最大值和最小值的问题。
(2)处理方法
①解析法:根据物体的平衡条件列出方程,在解方程时,采用数学知识求极值或者根据物理临界条件求极值。
②图解法:根据物体的平衡条件作出力的矢量图,画出平行四边形或者矢量三角形进行动态分析,确定最大值或最小值。
如图所示,质量为m的物体置于倾角为θ的固定斜面上,物体与斜面之间的动摩擦因数为μ,先用平行于斜面的推力F1作用于物体上使其恰能沿斜面匀速上滑,若改用水平推力F2作用于物体上,也恰能使物体沿斜面匀速上滑,则两次的推力之比为F1/ F2( )
A.cos θ+μsin θ
B.cos θ-μsin θ
C.1+μtan θ
D.1-μtan θ
经典例题
经典例题
谢
谢
观
看
