5.2视图同步练习(基础版)(含答案)北师大版数学九年级上册
文档属性
| 名称 | 5.2视图同步练习(基础版)(含答案)北师大版数学九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 332.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-26 21:36:27 | ||
图片预览




文档简介
5.2视图(基础卷)
一、选择题
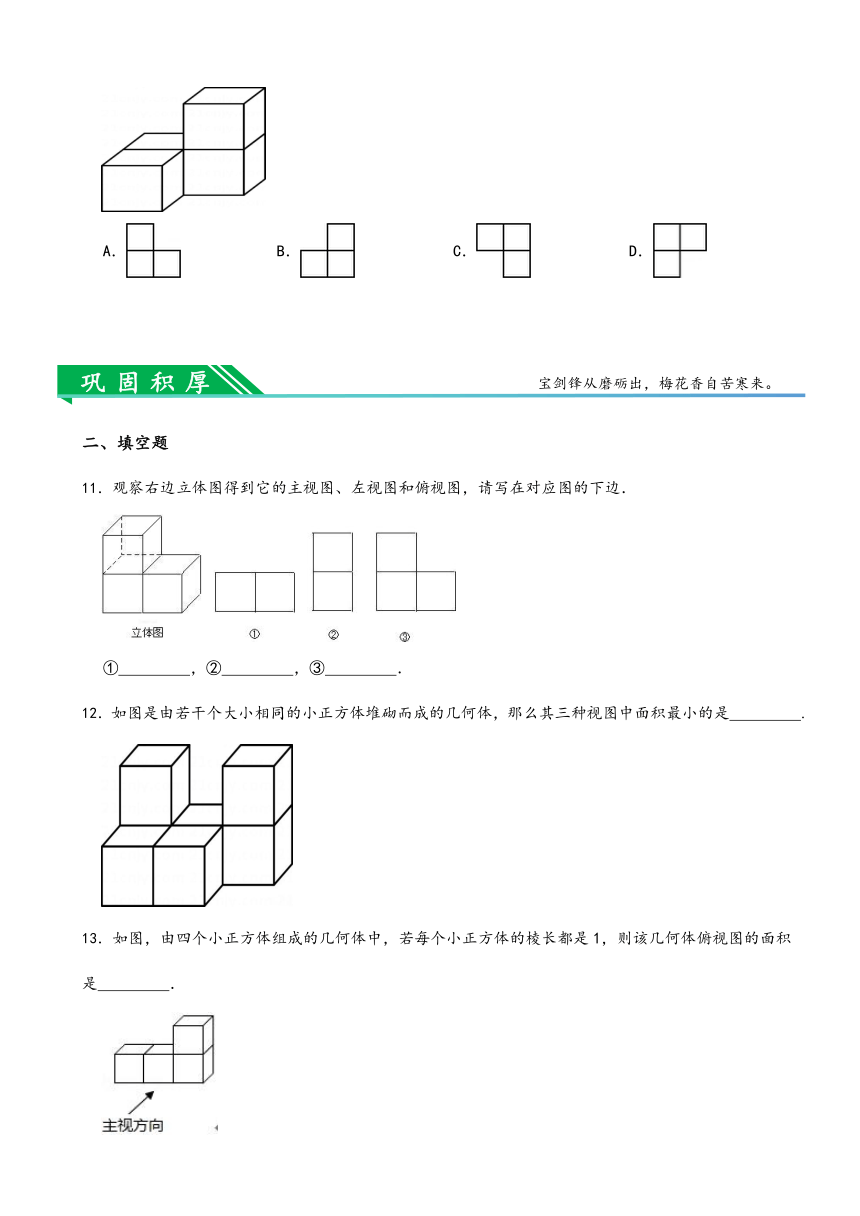
1.从左边观察如图所示的几何体,得到的形状图为( )
A. B. C. D.
2.如图是一个由5个相同的正方体组成的立体图形,其俯视图是( )
A. B. C. D.
3.如果用□表示1个立方体,用表示两个立方体叠加,用■表示三个立方体叠加,那么下面右图由6个立方体叠成的几何体,从正前方观察,可画出的平面图形是( )
A. B. C. D.
4.如图,一个水晶球摆件,它是由一个长方体和一个球体组成的几何体,其主视图是( )
A. B. C. D.
5.如图,这是一个机械模具,则它的俯视图是( )
A. B.
C. D.
6.如图,一个水晶球摆件,它是由一个长方体和一个球体组成的几何体,则其主视图是( )
A. B. C. D.
7.如图所示的几何体是由一个正方体和一个圆锥搭建而成,其左视图是( )
A. B. C. D.
8.如图所示几何体的左视图是( )
A. B.
C. D.
9.如图是一个由多个相同小正方体堆积而成的几何体的俯视图.图中所示数字为该位置小正方体的个数,则这个几何体的主视图是( )
A. B.
C. D.
10.如图是一个由4个相同的正方体组成的立体图形,它的左视图是( )
A. B. C. D.
二、填空题
11.观察右边立体图得到它的主视图、左视图和俯视图,请写在对应图的下边.
① ,② ,③ .
12.如图是由若干个大小相同的小正方体堆砌而成的几何体,那么其三种视图中面积最小的是 .
13.如图,由四个小正方体组成的几何体中,若每个小正方体的棱长都是1,则该几何体俯视图的面积是 .
14.如图,用 个同样大小的小立方体搭成一个大立方体,从上面小立方体中取走两个后得到的新几何体的三视图都相同,则他拿走的两个小正方体的序号是 (只填写满足条件的一种即可!)
15.如图,正三棱柱的底面周长为9,截去一个底面周长为3的正三棱柱,所得几何体的俯视图的周长是 .
三、作图题
16.画出物体的三种视图.
17.如图1,是一个长方体截成的几何体,请在网格中依次画出这个几何体的三视图.
18.如图是一个由9个相同的小立方块搭成的几何体.
(1)请画出它从三个方向看到的形状图.(不需要标序号①)
(2)将小正方体①移走后,所得几何体从三个方向看到的形状图没有发生变化的是 .
A.从正面看和从左面看
B.从正面看和从上面看
C.从左面看和从上面看
D.从正面看、从左面看 、从上面看
四、综合题
19.如图是一个组合(由两种常见的几何体组合)几何体的两种视图.
(1)请写出这个组合几何体是由哪两种几何体组成的;
(2)画出该组合几何体的左视图.
20.
(1)如图①是一个组合几何体,右边是它的两种视图,在右边横线上填写出两种视图名称;
(2)根据两种视图中尺寸(单位:cm),计算这个组合几何体的表面积.(π取3.14)
1.【答案】B
【解析】【解答】解:从左边看到有两列两行,最下面一行有两个小正方形,第二行左边有一个小正方形.
故答案为:B
【分析】左视图就是从几何体的左边所看到的平面图形,即可求解.
2.【答案】D
【解析】【解答】解:从上往下看,一共有3列,每一列只有一个正方形.
故答案为:D
【分析】俯视图就是从上往下看所看到的平面图形,据此可得到已知几何体的俯视图.
3.【答案】B
【解析】【解答】解:∵从正面看,左边两列都只有一个正方体,中间一列有三个正方体,右边一列是一个正方体.
∴可画出的平面图形是.
故答案为:B.
【分析】根据主视图是从正面看到的图形进行判定,结合用□表示1个立方体,用表示两个立方体叠加,用■表示三个立方体叠加,即可得出答案.
4.【答案】D
【解析】【解答】从正面看过去,可知组合体的上方是一个圆,圆下方是一个长方形,据此可知D项符合题意,
故答案为:D.
【分析】主视图:从物体正面所看的平面图形,注意:看到的棱画实线,看不到的棱画虚线,据此判断即可.
5.【答案】D
【解析】【解答】解:从上面看可得两个并排放着两个正方形,左边正方形内有一个内切圆.
故答案为:D.
【分析】俯视图:从物体上面所看的平面图形;注意:看到的棱画实线,看不到的棱画虚线,据此判断即可.
6.【答案】D
【解析】【解答】解:从正面看下边是一个矩形,矩形的上边是一个圆,
故答案为:D.
【分析】主视图:从物体正面所看的平面图形,注意:看到的棱画实线,看不到的棱画虚线,据此判断即可.
7.【答案】C
【解析】【解答】解:∵从左边看得到的图形是左视图,
∴该几何体从左边看第一层是一个三角形,第二层是一个小正方形.
故答案为:C.
【分析】从左面看圆锥得到的平面图形为三角形,从左面看正方体得到的平面图形为正方形,据此解答.
8.【答案】C
【解析】【解答】解:如图所示,几何体的左视图是:
故答案为:C.
【分析】左视图是从物体左面看所得到的图形;认真观察实物图,按照三视图的要求画图即可,其中看得到的棱长用实线表示,看不到的棱长用虚线的表示.
9.【答案】B
【解析】【解答】解:由俯视图中的数字可得:主视图有3列,从左到右分别是1,3,1个正方形.
故答案为:B.
【分析】由俯视图可知:主视图有3列,从左到右分别是1,3,1个正方形,据此逐一判断即可.
10.【答案】A
【解析】【解答】解:从左边看第一层是两个小正方形,第二层左边一个小正方形,
故答案为:A.
【分析】从左边看共有2列,从左到右小正方形的个数依次为2、1,据此判断即可.
11.【答案】俯视图;左视图;主视图
【解析】【解答】①是俯视图;②是左视图;③是主视图.
故答案为①是俯视图;②是左视图;③是主视图.
【分析】根据所给的立体图形求解即可。
12.【答案】左视图
【解析】【解答】解:如图,
该几何体主视图是由5个小正方形组成
左视图是由3个小正方形组成,
俯视图是由5个小正方形组成,
故三种视图面积最小的是左视图.
故答案为:左视图.
【分析】主视图,就是从物体的正面看得到的图形;俯视图,就是从物体的上面看得到的图形;左视图,就是从物体的左面看得到的图形;据此可知该几何体主视图是由5个小正方形组成,左视图是由3个小正方形组成,俯视图是由5个小正方形组成,再进行判断即可.
13.【答案】3
【解析】【解答】解:从上面看三个正方形组成的矩形,
矩形的面积为1×3=3.
故答案为:3.
【分析】其俯视图就是从上面向下看得到的正投影,应该是三个小正方形放在一列的一个长方形,该长方形的长为3,宽为1,根据面积计算方法即可算出答案。
14.【答案】 和 ,或者 和
【解析】【解答】解:要保证第二层每一横行和每一竖列上都有一个正方体,应利用正方形关于对角线所在直线的对称性拿走 和 ,或拿走 和 ,该物体的三视图都没有变化.
故答案为: 和 ,或者 和 .
【分析】第二层的各个几何体组成一个大的正方形,那么要保证第二层每一横行和每一竖列上都有一个正方体,应利用正方形关于对角线所在直线的对称性拿即可使该物体的三视图都没有变化.
15.【答案】8
【解析】【解答】解:从上边看是一个梯形:上底是1,下底是3,两腰是2,
周长是1+2+2+3=8,
故答案为:8.
【分析】根据从上边看得到的图形是俯视图,可得答案.
16.【答案】解:作图如下:
【解析】【分析】主视图是从几何体上面观察所得到的平面图形,左视图是从几何体左面观察所得到的平面图形,俯视图是从几何体上面观察所得到的平面图形,画图时需注意:看得见的棱用实线表示,看不见的棱用虚线表示.
17.【答案】解:三视图,如图所示.
【解析】【分析】观察该几何体,可得从正面看到的图形分为两部分,上方为一个等腰直角三角形,下方为一个矩形,从上面看到的图形为一个矩形且中间含有一条竖直的线,从左面看到的图形为一个矩形且中间含有一条虚线,据此作图.
18.【答案】(1)这个几何体从三个方向看到的图形如下:
(2)A
【解析】【解答】解:(2)将小正方体①移走后,所得几何体从三个方向看到的形状图如下:
所以从正面看和从左面看到的形状图没有发生变化,
故答案为:A.
【分析】(1)根据所给的几何体求解即可;
(2)根据题意,结合所给的正方体判断求解即可。
19.【答案】(1)解:根据题意得:这个几何体的上面是圆柱体,下面是长方体,
故由圆柱体与长方体组成
(2)解:由(1)得组合的几何体为圆柱体与长方体,
∴左视图与主视图一样,如图所示:
【解析】【分析】(1)根据常见几何体的三视图进行判断;
(2)由(1)得组合的几何体为圆柱体与长方体,然后根据左视图的概念进行作图.
20.【答案】(1)主,俯
(2)组合几何体的表面积=2×(8×5+8×2+5×2)+4×π×6=2×66+24×3.14=207.36(cm2).
【解析】【解答】(1)解:如图所示:
;
故答案为:主,俯;
【分析】(1)主视图就是从正面看得到的图形,俯视图就是从上面看得到的图形,左视图就是从左面看得到的图形,注意所有能看见的轮廓线都必须表现在视图中,据此即可判断得出答案;
(2)根据表面积=长方体的表面积+圆柱的侧面积进行计算.
一、选择题
1.从左边观察如图所示的几何体,得到的形状图为( )
A. B. C. D.
2.如图是一个由5个相同的正方体组成的立体图形,其俯视图是( )
A. B. C. D.
3.如果用□表示1个立方体,用表示两个立方体叠加,用■表示三个立方体叠加,那么下面右图由6个立方体叠成的几何体,从正前方观察,可画出的平面图形是( )
A. B. C. D.
4.如图,一个水晶球摆件,它是由一个长方体和一个球体组成的几何体,其主视图是( )
A. B. C. D.
5.如图,这是一个机械模具,则它的俯视图是( )
A. B.
C. D.
6.如图,一个水晶球摆件,它是由一个长方体和一个球体组成的几何体,则其主视图是( )
A. B. C. D.
7.如图所示的几何体是由一个正方体和一个圆锥搭建而成,其左视图是( )
A. B. C. D.
8.如图所示几何体的左视图是( )
A. B.
C. D.
9.如图是一个由多个相同小正方体堆积而成的几何体的俯视图.图中所示数字为该位置小正方体的个数,则这个几何体的主视图是( )
A. B.
C. D.
10.如图是一个由4个相同的正方体组成的立体图形,它的左视图是( )
A. B. C. D.
二、填空题
11.观察右边立体图得到它的主视图、左视图和俯视图,请写在对应图的下边.
① ,② ,③ .
12.如图是由若干个大小相同的小正方体堆砌而成的几何体,那么其三种视图中面积最小的是 .
13.如图,由四个小正方体组成的几何体中,若每个小正方体的棱长都是1,则该几何体俯视图的面积是 .
14.如图,用 个同样大小的小立方体搭成一个大立方体,从上面小立方体中取走两个后得到的新几何体的三视图都相同,则他拿走的两个小正方体的序号是 (只填写满足条件的一种即可!)
15.如图,正三棱柱的底面周长为9,截去一个底面周长为3的正三棱柱,所得几何体的俯视图的周长是 .
三、作图题
16.画出物体的三种视图.
17.如图1,是一个长方体截成的几何体,请在网格中依次画出这个几何体的三视图.
18.如图是一个由9个相同的小立方块搭成的几何体.
(1)请画出它从三个方向看到的形状图.(不需要标序号①)
(2)将小正方体①移走后,所得几何体从三个方向看到的形状图没有发生变化的是 .
A.从正面看和从左面看
B.从正面看和从上面看
C.从左面看和从上面看
D.从正面看、从左面看 、从上面看
四、综合题
19.如图是一个组合(由两种常见的几何体组合)几何体的两种视图.
(1)请写出这个组合几何体是由哪两种几何体组成的;
(2)画出该组合几何体的左视图.
20.
(1)如图①是一个组合几何体,右边是它的两种视图,在右边横线上填写出两种视图名称;
(2)根据两种视图中尺寸(单位:cm),计算这个组合几何体的表面积.(π取3.14)
1.【答案】B
【解析】【解答】解:从左边看到有两列两行,最下面一行有两个小正方形,第二行左边有一个小正方形.
故答案为:B
【分析】左视图就是从几何体的左边所看到的平面图形,即可求解.
2.【答案】D
【解析】【解答】解:从上往下看,一共有3列,每一列只有一个正方形.
故答案为:D
【分析】俯视图就是从上往下看所看到的平面图形,据此可得到已知几何体的俯视图.
3.【答案】B
【解析】【解答】解:∵从正面看,左边两列都只有一个正方体,中间一列有三个正方体,右边一列是一个正方体.
∴可画出的平面图形是.
故答案为:B.
【分析】根据主视图是从正面看到的图形进行判定,结合用□表示1个立方体,用表示两个立方体叠加,用■表示三个立方体叠加,即可得出答案.
4.【答案】D
【解析】【解答】从正面看过去,可知组合体的上方是一个圆,圆下方是一个长方形,据此可知D项符合题意,
故答案为:D.
【分析】主视图:从物体正面所看的平面图形,注意:看到的棱画实线,看不到的棱画虚线,据此判断即可.
5.【答案】D
【解析】【解答】解:从上面看可得两个并排放着两个正方形,左边正方形内有一个内切圆.
故答案为:D.
【分析】俯视图:从物体上面所看的平面图形;注意:看到的棱画实线,看不到的棱画虚线,据此判断即可.
6.【答案】D
【解析】【解答】解:从正面看下边是一个矩形,矩形的上边是一个圆,
故答案为:D.
【分析】主视图:从物体正面所看的平面图形,注意:看到的棱画实线,看不到的棱画虚线,据此判断即可.
7.【答案】C
【解析】【解答】解:∵从左边看得到的图形是左视图,
∴该几何体从左边看第一层是一个三角形,第二层是一个小正方形.
故答案为:C.
【分析】从左面看圆锥得到的平面图形为三角形,从左面看正方体得到的平面图形为正方形,据此解答.
8.【答案】C
【解析】【解答】解:如图所示,几何体的左视图是:
故答案为:C.
【分析】左视图是从物体左面看所得到的图形;认真观察实物图,按照三视图的要求画图即可,其中看得到的棱长用实线表示,看不到的棱长用虚线的表示.
9.【答案】B
【解析】【解答】解:由俯视图中的数字可得:主视图有3列,从左到右分别是1,3,1个正方形.
故答案为:B.
【分析】由俯视图可知:主视图有3列,从左到右分别是1,3,1个正方形,据此逐一判断即可.
10.【答案】A
【解析】【解答】解:从左边看第一层是两个小正方形,第二层左边一个小正方形,
故答案为:A.
【分析】从左边看共有2列,从左到右小正方形的个数依次为2、1,据此判断即可.
11.【答案】俯视图;左视图;主视图
【解析】【解答】①是俯视图;②是左视图;③是主视图.
故答案为①是俯视图;②是左视图;③是主视图.
【分析】根据所给的立体图形求解即可。
12.【答案】左视图
【解析】【解答】解:如图,
该几何体主视图是由5个小正方形组成
左视图是由3个小正方形组成,
俯视图是由5个小正方形组成,
故三种视图面积最小的是左视图.
故答案为:左视图.
【分析】主视图,就是从物体的正面看得到的图形;俯视图,就是从物体的上面看得到的图形;左视图,就是从物体的左面看得到的图形;据此可知该几何体主视图是由5个小正方形组成,左视图是由3个小正方形组成,俯视图是由5个小正方形组成,再进行判断即可.
13.【答案】3
【解析】【解答】解:从上面看三个正方形组成的矩形,
矩形的面积为1×3=3.
故答案为:3.
【分析】其俯视图就是从上面向下看得到的正投影,应该是三个小正方形放在一列的一个长方形,该长方形的长为3,宽为1,根据面积计算方法即可算出答案。
14.【答案】 和 ,或者 和
【解析】【解答】解:要保证第二层每一横行和每一竖列上都有一个正方体,应利用正方形关于对角线所在直线的对称性拿走 和 ,或拿走 和 ,该物体的三视图都没有变化.
故答案为: 和 ,或者 和 .
【分析】第二层的各个几何体组成一个大的正方形,那么要保证第二层每一横行和每一竖列上都有一个正方体,应利用正方形关于对角线所在直线的对称性拿即可使该物体的三视图都没有变化.
15.【答案】8
【解析】【解答】解:从上边看是一个梯形:上底是1,下底是3,两腰是2,
周长是1+2+2+3=8,
故答案为:8.
【分析】根据从上边看得到的图形是俯视图,可得答案.
16.【答案】解:作图如下:
【解析】【分析】主视图是从几何体上面观察所得到的平面图形,左视图是从几何体左面观察所得到的平面图形,俯视图是从几何体上面观察所得到的平面图形,画图时需注意:看得见的棱用实线表示,看不见的棱用虚线表示.
17.【答案】解:三视图,如图所示.
【解析】【分析】观察该几何体,可得从正面看到的图形分为两部分,上方为一个等腰直角三角形,下方为一个矩形,从上面看到的图形为一个矩形且中间含有一条竖直的线,从左面看到的图形为一个矩形且中间含有一条虚线,据此作图.
18.【答案】(1)这个几何体从三个方向看到的图形如下:
(2)A
【解析】【解答】解:(2)将小正方体①移走后,所得几何体从三个方向看到的形状图如下:
所以从正面看和从左面看到的形状图没有发生变化,
故答案为:A.
【分析】(1)根据所给的几何体求解即可;
(2)根据题意,结合所给的正方体判断求解即可。
19.【答案】(1)解:根据题意得:这个几何体的上面是圆柱体,下面是长方体,
故由圆柱体与长方体组成
(2)解:由(1)得组合的几何体为圆柱体与长方体,
∴左视图与主视图一样,如图所示:
【解析】【分析】(1)根据常见几何体的三视图进行判断;
(2)由(1)得组合的几何体为圆柱体与长方体,然后根据左视图的概念进行作图.
20.【答案】(1)主,俯
(2)组合几何体的表面积=2×(8×5+8×2+5×2)+4×π×6=2×66+24×3.14=207.36(cm2).
【解析】【解答】(1)解:如图所示:
;
故答案为:主,俯;
【分析】(1)主视图就是从正面看得到的图形,俯视图就是从上面看得到的图形,左视图就是从左面看得到的图形,注意所有能看见的轮廓线都必须表现在视图中,据此即可判断得出答案;
(2)根据表面积=长方体的表面积+圆柱的侧面积进行计算.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
