6.2反比例函数的图象与性质同步练习(培优版)(含答案)北师大版数学九年级上册
文档属性
| 名称 | 6.2反比例函数的图象与性质同步练习(培优版)(含答案)北师大版数学九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 581.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-26 00:00:00 | ||
图片预览



文档简介
6.2反比例函数的图象与性质(培优卷)
一、选择题
1.已知、、为双曲线上的三个点,且,则以下判断正确的是( )
A.若,则 B.若,则
C.若,则 D.若,则
2.如图,的三个顶点的坐标分别为,,,将绕点顺时针旋转一定角度后使落在轴上,与此同时顶点恰好落在双曲线的图象上,则该反比例函数表达式为( )
A. B. C. D.
3.如图,平行四边形的顶点在双曲线上,顶点在双曲线上,中点恰好落在轴上,已知,则的值为( )
A.-8 B.-6 C.-4 D.-2
4.如图, 中, , ,点 在反比例函数 的图象上, 交反比例函数 的图象于点 ,且 ,则 的值为( )
A.-2 B.-4 C.-6 D.-8
5.如图,在平面直角坐标系中,菱形ABCO的顶点O在坐标原点,且与反比例函数y=的图象相交于A(m,3),C两点,已知点B(,),则k的值为( )
A.-6 B.-6 C.-12 D.-12
6.已知点A是双曲线y= 在第一象限分支上的一个动点,连接AO并延长交另一分支于点B,以AB为边作等边三角形ABC,点C在第四象限内,随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y= (x>0)上运动,则k的值是( )
A.3 B. C.﹣3 D.﹣
7.如图,点A是反比例图数y= (x<0)图象上一点,AC⊥x轴于点C,与反比例函数y= (x<0)图象交于点B,AB=2BC,连接OA、OB,若△OAB的面积为3,则m+n=( )
A.﹣4 B.﹣6 C.﹣8 D.﹣12
8.如图,点A是反比例函数y=(x<0)的图象上的一点,过点A作平行四边形ABCD,使点B、C在x轴上,点D在y轴上已知平行四边形ABCD的面积为6,则k的值为( )
A.6 B.-6 C.3 D.-3
9.如图,正方形ABCD位于第一象限,边长为3,点A在直线y=x上,点A的横坐标为1,正方形ABCD的边分别平行于x轴、y轴.若双曲线 与正方形ABCD有公共点,则k的取值范围为( )
A.1<k<9 B.2≤k≤34 C.1≤k≤16 D.4≤k<16
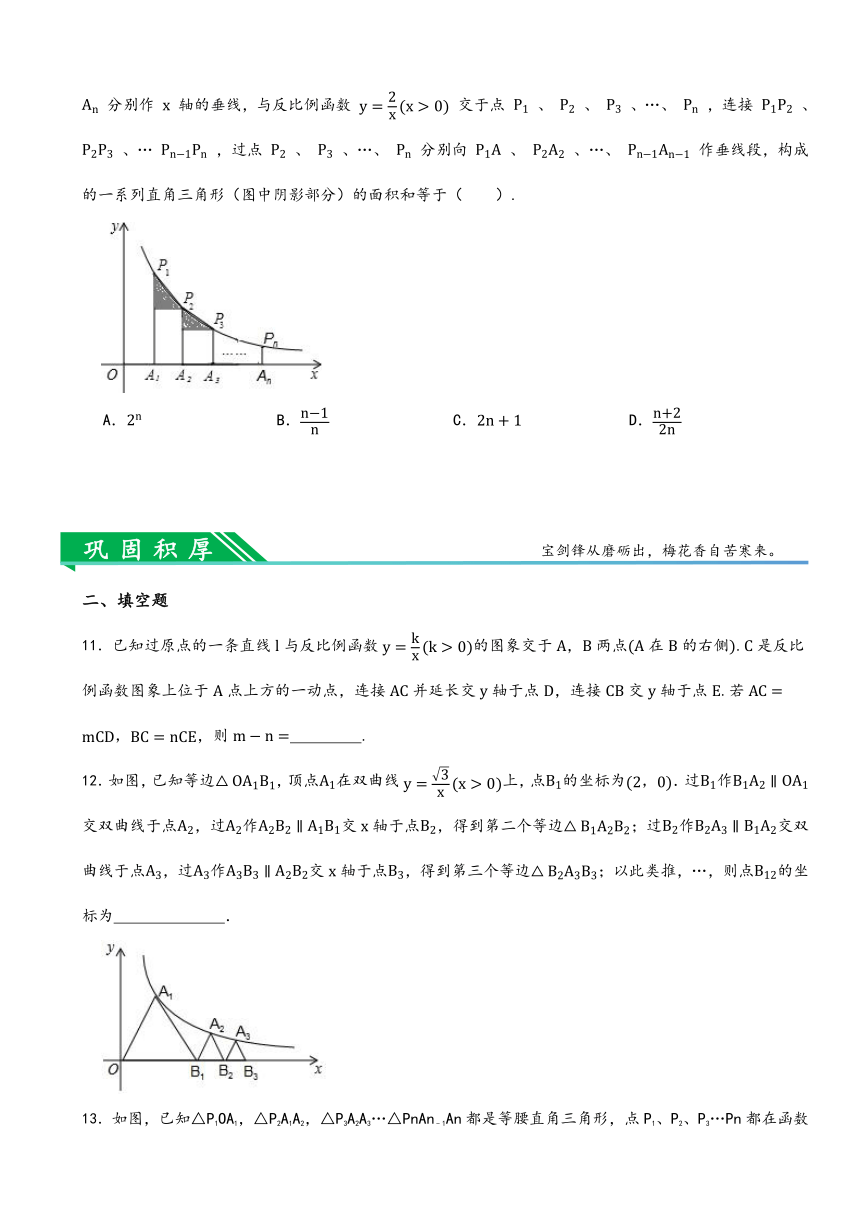
10.如图,在 轴正半轴上依次截取 ,过点 、 、 、…… 分别作 轴的垂线,与反比例函数 交于点 、 、 、…、 ,连接 、 、… ,过点 、 、…、 分别向 、 、…、 作垂线段,构成的一系列直角三角形(图中阴影部分)的面积和等于( ).
A. B. C. D.
二、填空题
11.已知过原点的一条直线与反比例函数的图象交于,两点在的右侧.是反比例函数图象上位于点上方的一动点,连接并延长交轴于点,连接交轴于点.若,则 .
12.如图,已知等边,顶点在双曲线上,点的坐标为.过作交双曲线于点,过作交轴于点,得到第二个等边;过作交双曲线于点,过作交轴于点,得到第三个等边;以此类推,…,则点的坐标为 .
13.如图,已知△P1OA1,△P2A1A2,△P3A2A3…△PnAn﹣1An都是等腰直角三角形,点P1、P2、P3…Pn都在函数y=(x>0)的图象上,斜边OA1、A1A2、A2A3…An﹣1An都在x轴上.则点A2021的坐标为 .
14.如图,将一块直角三角板OAB放在平面直角坐标系中,B(2,0),∠AOB=60°,点A在第一象限,过点A的双曲线为y= ,在x轴上取一点P,过点P作直线OA的垂线l,以直线l为对称轴,线段OB经轴对称变换后的像是O′B′.设P(t,0),当O′B′与双曲线有交点时,t的取值范围是 .
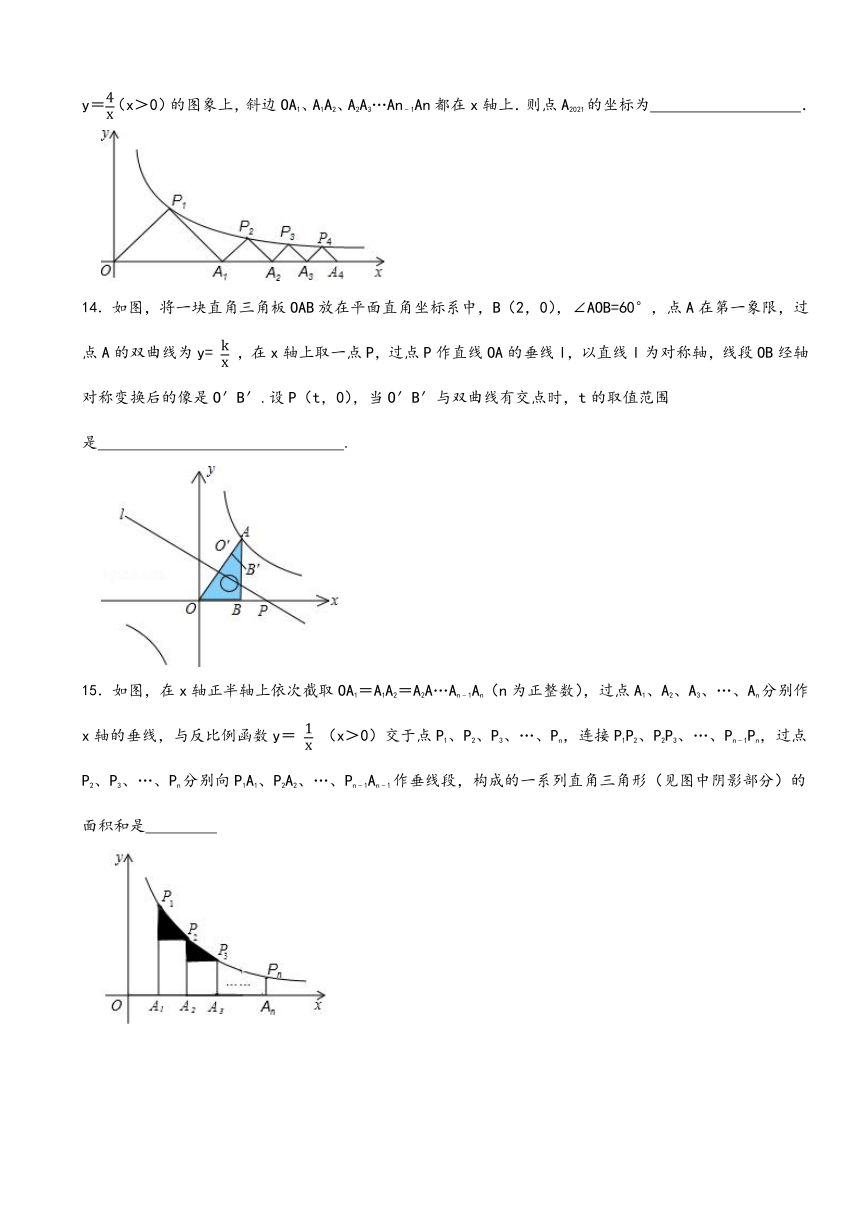
15.如图,在x轴正半轴上依次截取OA1=A1A2=A2A…An﹣1An(n为正整数),过点A1、A2、A3、…、An分别作x轴的垂线,与反比例函数y= (x>0)交于点P1、P2、P3、…、Pn,连接P1P2、P2P3、…、Pn﹣1Pn,过点P2、P3、…、Pn分别向P1A1、P2A2、…、Pn﹣1An﹣1作垂线段,构成的一系列直角三角形(见图中阴影部分)的面积和是
三、综合题
16.如图1,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点B在反比例函数y=(k>0)的第一象限内的图象上,OA=4,OC=3,动点P在y轴的右侧,且满足S△PCO=S矩形OABC.
(1)若点P在这个反比例函数的图象上,求点P的坐标;
(2)连接PO、PC,求PO+PC的最小值;
(3)若点Q是平面内一点,使得以B、C、P、Q为顶点的四边形是菱形,请你直接写出满足条件的所有点Q的坐标.
17.如图,平行四边形OABC的边OA在x轴的正半轴上,,,CD平分∠OCB,CD交OA于点D,作DE⊥CD交AB于点E,反比例函数的图象经过点C与点E.
(1)求k的值及直线CD的解析式;
(2)求证:;
(3)求点E的坐标.
18.已知一块矩形草坪的两边长分别是2米与3米,现在要把这个矩形按照如图1的方式扩大到面积为原来的2倍,设原矩形的一边加长a米,另一边长加长b米,可得a与b之间的函数关系式b=﹣2.某班“数学兴趣小组”对此函数进一步推广,得到更一般的函数y=﹣2,现对这个函数的图象和性质进行了探究,研究过程如下,请补充完整:
(1)类比反比例函数可知,函数y=﹣2的自变量x的取值范围是 ,这个函数值y的取值范围是 .
(2)“数学兴趣小组”进一步思考函数y=|﹣2|的图象和性质,请根据函数y=﹣2的图象,画出函数y=|﹣2|的图象;
(3)结合函数y=|﹣2|的图象解答下列问题:
①求出方程|﹣2|=0的根;
②如果方程|﹣2|=a有2个实数根,请直接写出a的取值范围.
19.已知点A(3,m+2),B(m+4,2)都在反比例函数y的图像上.
(1)求m,k的值;
(2)如图①,已知反比例函数y的图像上有两点P1(x1,y1),P2(x2,y2),且0<x1<x2<3,分别过P1,P2向x轴作垂线,垂足分别为M1,M2,过P1,P2向y轴作垂线,垂足分别为N1,N2.若记四边形P1M1ON1和四边形P2M2ON2的周长分别为C1,C2,试比较C1和C2的大小;并说明理由.
(3)如图②,若点B关于原点O对称点为C,点Q为双曲线AB段上任一动点,试探究∠ACQ与∠ABQ大小关系,并说明理由.
20.如图,四边形OABC为正方形,反比例函数的图象过AB上一点E,BE=2,.
(1)求k的值.
(2)反比例函数的图象与线段BC交于点D,直线y=ax+b过点D及线段AB的中点F,探究直线OF与直线DF的位置关系,并证明.
(3)点P是直线OF上一点,当PD+PC的值最小时,求点P的坐标.
1.【答案】D
【解析】【解答】解:A、∵y=-,若x1x2>0,
当x1<x2<x3<0时,
∴y3>y2>y1>0,
∴y1y3>0,
∴A选项错误,不符合题意;
B、∵y=-,若x1x3<0,
当x1<0<x2<x3时,
∴y1>0>y3>y2,
∴y1y2<0,
∴B选项错误,不符合题意;
C、∵y=-,若x2x3>0,
当x1<0<x2<x3时,
∴y1>0>y3>y2,
∴y1y3<0,
∴C选项错误,不符合题意;
D、∵y=-,若x2x3<0,
∴x1<x2<0<x3时,
∴y2>y1>0>y3,
∴y1y3<0,
∴D选项正确,符合题意.
故答案为:D.
【分析】根据反比例函数增减性,结合每个选项条件,求得对应y的正负号,再逐项进行分析判断即可.
2.【答案】D
【解析】【解答】解:,,,
轴,,,
,
将绕点顺时针旋转一定角度后使落在轴上,
,,,
在中,,
,
设,
①,②,
①②得③,
把③代入①整理得,解得(舍去),,
当时,,
,
把代入得.
∴,
故答案为:D.
【分析】利用A、B、C的坐标及勾股定理求出,由旋转的性质可得,,,在中,利用勾股定理求出OA',即得A’(0,8),设,可得①,②,联立①②可求出a、b值,即得C'坐标,将其代入中即可求出k值.
3.【答案】C
【解析】【解答】解:连接OB,过点B作BD⊥y轴于点D,过点C作CE⊥y于点E,
∵点P是BC的中点
∴PC=PB
∵
∴
∴
∵
∴
∵点B在双曲线上
∴
∴
∴
∴
∵点C在双曲线上
∴
∴.
故答案为:C.
【分析】连接OB,过点B作BD⊥y轴于点D,过点C作CE⊥y于点E,利用AAS证明△CPE≌△BPD,根据全等三角形的对应边相等得CE=BD,根据平行四边形的性质及同底等高的三角形面积相等得,根据反比例函数k的几何意义得,从而可得,最后再根据反比例函数k的几何意义结合图象所在的象限得出k的值.
4.【答案】D
【解析】【解答】解:过点A作AD⊥x轴,过点C作CE⊥x轴,过点B作BF⊥x轴
∴CE∥AD,∠CEO=∠BFO=90°
∵
∴∠COE+∠FOB=90°,∠ECO+∠COE=90°
∴∠ECO=∠FOB
∴△COE∽△OBF∽△AOD
又∵ ,
∴ ,
∴ ,
∴
∵点 在反比例函数 的图象上
∴
∴
∴ ,解得k=±8
又∵反比例函数位于第二象限,
∴k=-8
故答案为:D.
【分析】过点A作AD⊥x轴,过点C作CE⊥x轴,过点B作BF⊥x轴,由平行线的性质可得∠CEO=∠BFO=90°,根据同角的余角相等可得∠ECO=∠FOB,证明△COE∽△OBF∽△AOD,根据已知条件结合相似三角形的性质可得,根据反比例函数k的几何意义可得S△BOF=1,进而求出S△COE,再次利用反比例函数k的几何意义就可求出k的值.
5.【答案】A
【解析】【解答】解:作AE⊥x轴交x轴于点E,作CF⊥x轴交x轴于点F,作BD∥x轴交AE于点D,AB与y轴交点记为M;
∵四边形AOCB是菱形,
∴AB∥CO,AB=CO,
∴∠ABO=∠COB,
又∵BD∥x轴,
∴∠DBO=∠FOB,
∴∠ABD=∠COF,
∵AD⊥BD,CF⊥OF,
∴∠ADB=∠CFO=90°,
在△ADB和△CFO中,
,
∴△ADB≌△CFO(AAS),
∴AD=CF,
∵A(m,),B(,)
∴AD=,
∴CF=,
∵四边形AOCB是菱形,
∴∠AOB=∠COB,
∵B(,),
∴∠BOF=∠BOM=45°,
∵AE∥y轴,
∴∠EAO=∠AOM,
∴∠AOM=∠COF,
∴∠EAO=∠COF,
∵AE⊥x,CF⊥x轴,
∴∠AEO=∠CFO,
在△AEO和△OFC中,
∴△AEO≌△OFC(AAS),
∴OE=CF=,
∴点A的坐标为(,),
∵点A在反比例函数图象上,
∴ ,
解得:k=-6.
故答案为:A.
【分析】作AE⊥x轴交x轴于点E,作CF⊥x轴交x轴于点F,作BD∥x轴交AE于点D,AB与y轴交点记为M,由菱形的性质可得AB∥CO,AB=CO,根据平行线的性质可得∠ABO=∠COB,∠DBO=∠FOB,则
∠ABD=∠COF,证明△ADB≌△CFO,得到AD=CF,根据点A、B的坐标可得AD=CF=,证明△AEO≌△OFC,得到OE=CF=,则A(-,3),然后代入y=中就可求出k的值.
6.【答案】C
【解析】【解答】解:如图,连接OC,
根据反比例函数的中心对称性质,得 OA=OB,
∵△ABC是等边三角形,
∴OC⊥AB,∠OCA=30°,
∴OC:OA= ,
过点A作AD⊥x轴,垂足为点D,过点C作CE⊥x轴,垂足为点E,
∴∠ADO=∠OEC=90°,
∵∠AOD+∠OAD =90°,∠AOD+∠COE=90°,
∴∠OAD=∠COE,
∴△DOA∽△ECO,
∴EC:DO=OE:AD=OC:AD,
∴EC= DO,OE= AD,
设点A(a,b),则DO=a,AD=b,ab=1,
∵点C在第四象限,
∴点C的坐标为( b,- a),
∵点C始终在双曲线y= (x>0)上运动,
∴k=(- a)× b= -3ab= -3.
故答案为:C.
【分析】连接OC,则OA=OB,由等边三角形的性质可得OC⊥AB,∠OCA=30°,则OC:OA=,过点A作AD⊥x轴,垂足为点D,过点C作CE⊥x轴,垂足为点E,由同角的余角相等可得∠OAD=∠COE,证明△DOA∽△ECO,由相似三角形的性质表示出EC、OE,设点A(a,b),则DO=a,AD=b,ab=1,则点C的坐标为(b,-a),代入y=(x>0)中求解可得k的值.
7.【答案】D
【解析】【解答】解:∵AC⊥x轴于点C,与反比例函数y= (x<0)图象交于点B,
而m<0,n<0,
∴S△AOC= |m|=﹣ m,S△BOC= |n|=﹣ n,
∵AB=2BC,
∴S△ABO=2S△OBC=3,
即﹣ n= ,解得n=﹣3
∵﹣ m=3+ ,解得m=﹣9,
∴m+n=﹣9﹣3=﹣12.
故答案为:D.
【分析】利用反比例函数比例系数k的几何意义得到S△AOC= |m|=- m,S△BOC= |n|=- n,利用AB=2BC得到S△ABO=2S△OBC=3,所以- n= ,解得n=-3,再利用- m=3+ 得m=-9,然后计算m+n的值.
8.【答案】B
【解析】【解答】解:过点A作AE⊥BC,垂足为点E
∵四边形ABCD为平行四边形
∴AD∥x轴
∴四边形ADOE为矩形
∴平行四边形ABCD的面积=矩形ADOE的面积
∵矩形ADOE面积=|-k|,
∴|-k|=6
∵k<0
∴k=-6
故答案为:B.
【分析】过点A作AE⊥BC,垂足为点E,根据平行四边形的性质即可证明四边形ADOE为矩形,根据反比例函数的解析式k的含义即可得到答案。
9.【答案】C
【解析】【解答】解:点A在直线y=x上,其中A点的横坐标为1,则把x=1代入y=x解得y=1,则A的坐标是(1,1),∵AB=BC=3,∴C点的坐标是(4,4),∴当双曲线 经过点(1,1)时,k=1;当双曲线 经过点(4,4)时,k=16,因而1≤k≤16.
故答案为:C.
【分析】先求出点A的坐标,再求出点C的坐标,分别求出双曲线经过点A和点C时的k的值,即可求出k的取值范围.
10.【答案】B
【解析】【解答】∵
∴设 (1, ), (1, ), (1, )… (1, )
∵ 、 、 、…、 在反比例函数 的图像上
∴
∴
∴
∵
∴
…
∴
因此答案选择B.
【分析】由 可设 点的坐标为(1, ), 点的坐标为(1, ), 点的坐标为(1, )… 点的坐标为(1, ),把x=1,x=2,x=3代入反比例函数的解析式即可求出 的值,再由三角形的面积公式可以得出 … 的值,即可得出答案.
11.【答案】2
【解析】【解答】解:如图所示,过点分别作轴的垂线,垂足分别为,
,
,
,
则,
根据对称性可得
∴
故答案为:2.
【分析】过点A、B、C分别作y轴的垂线,垂足分别为F、G、H,则CF∥AG∥BH,证明△DFC∽△DGA,△FCE∽△HBE,根据相似三角形的性质可得BH=(n-1)CF,根据平行线分线段成比例的性质可得AG=(m+1)CF,根据对称性可得BH=AG=(m+1)CF,联立化简可得m与n的关系.
12.【答案】(,0)
【解析】【解答】解:如图,作A2C⊥x轴于点C,设B1C=a,则A2C=,
OC=OB1+B1C=2+a,A2(2+a,).
∵点A2在双曲线上,
∴(2+a) =,
解得a=-1,或a=--1(舍去),
∴OB2=OB1+2B1C=2+2-2=2,
∴点B2的坐标为(2,0);
作A3D⊥x轴于点D,设B2D=b,则A3D=b,
OD=OB2+B2D=2+b,A2(2+b,b).
∵点A3在在双曲线上,
∴(2+b) b=,
解得b=-+,或b=--(舍去),
∴OB3=OB2+2B2D=2-2+2=2,
∴点B3的坐标为(2,0);
同理可得点B4的坐标为(2,0)即(4,0);
以此类推…,
∴点Bn的坐标为(2,0),
当n=12时,2
∴点B12的坐标为(4,0),
故答案为(4,0).
【分析】如图,作A2C⊥x轴于点C,根据等边三角形及反比例函数图象上点的坐标特征分别求出B1、B2、B3、B4的坐标,从而得出规律点Bn的坐标为(2,0),继而求出B12的坐标即可.
13.【答案】(,0)
【解析】【解答】解:可设点P1(x,y),
根据等腰直角三角形的性质可得:x=y,
又∵y=,
则x2=4,
∴x=±2(负值舍去),
再根据等腰三角形的三线合一,得A1的坐标是(4,0),
设点P2的坐标是(4+y,y),
又∵y=,则y(4+y)=4,即y2+4y-4=0
解得,y1=-2+2,y2=-2-2,
∵y>0,
∴y=2-2,
再根据等腰三角形的三线合一,得A2的坐标是(4,0);
可以再进一步求得点A3的坐标是(4,0),推而广之,则An点的坐标是(4,0).
故点A2021的坐标为 (4,0).
故答案是:(4,0).
【分析】先根据等腰直角三角形的性质得出P1的横、纵坐标相等,再结合双曲线的解析式得出P1的坐标,则根据等腰三角形的三线合一求得A1的坐标,同样根据等腰直角三角形的性质、点A1的坐标和双曲线的解析式求得A2的坐标,根据A1、A2的坐标特征即可发现其规律。
14.【答案】4≤t≤2 或﹣2 ≤t≤﹣4
【解析】【解答】解:当点O′与点A重合时,
∵∠AOB=60°,过点P作直线OA的垂线l,以直线l为对称轴,线段OB经轴对称变换后是O′B′,AP=OP,
∴△AOP′是等边三角形,
∵B(2,0),
∴BO=BP′=2,
∴点P的坐标是(4,0),
即当P的坐标是(4,0)时,直线O B 与双曲线有交点O′;
当B′在双曲线上时,作B′C⊥OP于C,
∵BP=B′P,∠B′BP=60°,
∴△BB′P是等边三角形,
∴BP=B′P=t﹣2,
∴CP= (t﹣2),B′C= (t﹣2),
∴OC=OP﹣CP= t+1,
∴B′的坐标是( t+1, (t﹣2)),
∵∠ABO=90°,∠AOB=60°,OB=2,
∴OA=4,AB=2 ,
∴A(2,2 ),
∵A和B′都在双曲线上,
∴( t+1) (t﹣2))=2×2 ,
解得:t=±2 ,
∴t的取值范围是4≤t≤2 或﹣2 ≤t≤﹣4.
故答案为:4≤t≤2 或﹣2 ≤t≤﹣4.
【分析】当点O'与点A重合时,过点P作直线OA的垂线l,以直线l为对称轴,线段OB经轴对称变换后是O′B′,得出AP=OP,结合∠AOB=60°,得出△AOP是等边三角形,根据等边三角形的性质求出点P的坐标,进一步解直角△AOB,根据A和B′都在双曲线上,建立关于t的代数式求解,即可得出t的范围.
15.【答案】
【解析】【解答】设OA1=A1A2=A2A3=…=An﹣1An=1,
∴P1(1,y1),P2(2,y2),P3(3,y3),…Pn(n,yn),
∵P1,P2,P3…Pn在反比例函数y= (x>0)的图象上,
∴y1=1,y2= ,y3= …yn= ,
∴S1= ×1×(y1﹣y2)= ×(1﹣ ),
S2= ×1×(y2﹣y3)= ×( ﹣ ),
S3= ×1×(y3﹣y4)= ×( ﹣ ),
…
Sn﹣1= ( ﹣ ),
∴S1+S2+S3+…+Sn﹣1═ (1﹣ + ﹣ + ﹣ +…+ ﹣ )= .
故答案为: .
【分析】设OA1=A1A2=A2A3=…=An﹣1An=1,得出P1(1,y1),P2(2,y2),P3(3,y3),…Pn(n,yn),再根据P1,P2,P3…Pn在反比例函数y= (x>0)的图象上,得出y1=1,y2= ,y3= …yn= ,推出S1的的答案,从而得出S2、S3、…,从而得出Sn﹣1= ( ﹣ ),即可得出答案。
16.【答案】(1)解:∵四边形OABC是矩形,OA=4,OC=3,
∴点B的坐标为(4,3),
∵点B在反比例函数的第一象限内的图象上
∴k=12,
∴反比例函数解析式为y=,
设点P的横坐标为m(m>0),
∵.
∴,
∴,
当点,P在这个反比例函数图象上时,则 ,
∴点P的坐标为(3,4).
(2)解:取点F(6,0),连接FP,CF,
∴O、F关于直线对称,
由(1)知,点P的横坐标为3,
∴点P在直线上,
∴PF=PO,
∴PC+PO=PF+PC,
∴当C、P、F三点共线时,PF+PC即PC+PO有最小值,最小值即为CF,
∴PO+PC的最小值=PF+PC=CF=;
(3)解:或或或
【解析】【解答】(3)解:设点Q的坐标为(m,n),点P的坐标为(3,t)
如图3-1所示,当BP为以B、C、P、Q为顶点的四边形的边时,由菱形的性质可知PB=BC=4,
∴,
∴或,
∴点P的坐标为或,
∴点Q的坐标为或;
如图3-2所示,当BP为以B、C、P、Q为顶点的四边形的对角线时,由菱形的性质可知PC=BC=4,
∴,
∴或,
∴点P的坐标为或,
∴同理可得点Q的坐标为或;
综上所述,点Q的坐标为或或或
【分析】(1)先确定点B坐标,从而确定反比例函数解析式,设点P的横坐标为m(m>0), 根据 构建方程求出m值,即得点P坐标;
(2)取点F(6,0),连接FP,CF, 即得O、F关于直线对称, 由(1)可推出点P在直线x=3上,可得PF=PO,即得PC+PO=PF+PC,当C、P、F三点共线时,PF+PC即PC+PO有最小值,最小值即为CF,利用勾股定理求出CF的长即可;
(3)分两种情况:①当BP为以B、C、P、Q为顶点的四边形的边时,②当BP为以B、C、P、Q为顶点的四边形的对角线时,根据菱形的性质分别求解即可.
17.【答案】(1)解:如图1,过C点作CH垂直x轴,
∵,,
∴,
∴,,
∴点,
∴反比例函数的系数,
∵在平行四边形OABC,,
∴,
又∵CD平分∠OCB,
∴,
∴是等边三角形,
∴,即点D,
∵点C,点D,
∴直线的解析式是
(2)证明:∵是等边三角形,
∴,
又∵DE⊥CD,
∴,
∵,
∴,
∴,
∴.
(3)解:过E点作EQ垂直x轴,设,
∵,
∴,,
∴点
点在反比例函数的图象上,
∴
∴或(舍去),则点的坐标是)
【解析】【分析】(1)过C点作CH垂直x轴,利用解直角三角形求出点C坐标,再利用带动系数法求出值;先证△OCD是等边三角形,可得OD=OC=12,即得D(12,0),利用待定系数法求出直线CD解析式即可;
(2)由等边三角形的性质可得∠CDO=60°,从而推出, 利用等腰三角形的性质即得结论;
(3)过E点作EQ垂直x轴,设, 可得,, 即点,将点E坐标代入反比例函数解析式中即可求解.
18.【答案】(1)x≠﹣3;y≠﹣2
(2)解:函数y=|﹣2|的图象,如图所示:
(3)解:①方程|﹣2|=0该方程的根是x=3;
②如果方程|﹣2|=a有2个实数根,则a的取值范围是0<a<2或a>2.
【解析】【解答】解:(1)y=﹣2的自变量x的取值范围是x≠﹣3,这个函数值y的取值范围是y≠﹣2,
故答案为:x≠﹣3;y≠﹣2.
【分析】(1)根据分式有意义的条件得出自变量x的取值范围是x≠-3,根据≠0,得出函数值y的取值范围是y≠-2,即可得出答案;
(2)y=﹣2的图象的x轴上方部分沿x轴翻折,即可得出函数y=|﹣2|的图象;
(3)①利用图象法即可得出方程|﹣2|=0该方程的根是x=3;
②利用图象法即可得出a的取值范围是0<a<2或a>2.
19.【答案】(1)解:∵点A(3,m+2),B(m+4,2)都在反比例函数 y= 的图象上.
∴3(m+2)= 2(m+4),∴解得:m=2.
∴A(3,4)、B(6,2).∴k=12;
(2)解: ,
∵∴
∴
∴ .
(3)解:∠ACQ=∠ABQ理由:
设AC 、QC分别交x轴于D、G两点,延长AB、QB分别x轴于E、F两点,
分别求出直线AB、直线AC的解析式为: 、 ,
得到:E(9,0)、D(-3,0)
作AH⊥DF于H,则DH=EH=6,
∴AD=AE ,∠ADE=∠AED
设Q( ),直线BQ的解析式为:
将点B(6,2)、Q( )代入,得:
解得:
∴直线BQ的解析式为:
当 时,
∴
同理可得:直线CQ的解析式为: ,
作QI⊥x轴
∵IG=n-(n-6)=6,IF=n+6-n=6
∴IG=IF
∴∠QGF=∠F
∵∠ADE=∠ACQ+∠DGC=∠ACQ+∠QGF
∠AED=∠F+∠EBF=∠F+∠ABQ
∴∠ACQ+∠QGF=∠F+∠ABQ
∴∠ACQ=∠ABQ
【解析】【分析】(1)根据 点A(3,m+2),B(m+4,2)都在反比例函数y的图像上 ,将点A,B的坐标分别代入反比例函数,得到关于m的一元一次方程,解方程求出m的值,再将m代入点A,B中,代入其中一个点即可求k;
(2)根据矩形的周长公式()和反比例函数解析式分别表示出两个四边形的周长,然后作差得,根据题意 0<x1<x2<3,可得,进而可判断;
(3)设AC 、QC分别交x轴于D、G两点,延长AB、QB分别x轴于E、F两点,利用待定系数法分别求出直线AB、直线AC的解析式为: 、 ,得到:E(9,0)、D(-3,0),作AH⊥DF于H,则DH=EH=6,根据等腰三角形的判定(高线、中线为同一条直线的三角形是等腰三角形)可得AD=AE ,∠ADE=∠AED,设Q( ),直线BQ的解析式为: ,代入点B和点Q的坐标,得到直线BQ的解析式为: ,进而得出点F的坐标,同理可得:直线CQ的解析式为: , ,作QI⊥x轴,可得IG=IF,根据等边对等角得到∠QGF=∠F,利用三角形的外角性质(三角形的外角等于与它不相邻的两个内角的和)和等量代换即可得到∠ACQ=∠ABQ..
20.【答案】(1)解:∵四边形OABC是正方形,
∴AO=AB,∠OAB=90°,
∵,
设AE=3x,则OE=5x,由勾股定理得AO=4x,
∴3x+2=4x,
∴x=2,
∴AE=3x=6,AO=4x=8,
∴点E坐标为(6,8),
∴k=6×8=48;
(2)解:OF⊥DF,理由如下:
将x=8代入y=得y=6,
∴D(8,6),
∴BD=BC-CD=8-6=2,
∵点F是线段AB的中点,
∴AF=BF=4,
∵,∠OAF=∠FBD=90°,
∴△AOF∽△BFD,
∴∠AOF=∠BFD,
∴∠AFO+∠BFD=∠AFO+∠AOF=90°,
∴∠OFD=180°-(∠AFO+∠BFD)=90°,
∴OF⊥DF;
(3)解:延长DF交y轴于点G,连接CG交OF于点P,则点P为所求作点,
∵四边形OABC为正方形,∠AFG=∠BFD,AF=BF,
∴△AFG≌△BFD(AAS),
∴AG=BD=2,GF=DF,
由(2)得OF⊥DF,
∴OF为线段DG的垂直平分线,
∴PD+PC的最小值=PG+PC=CG,
∵OC=OA=8,
∴C(8,0),G(0,10),
设直线CG解析式为y=mx+n,代入C(8,0),G(0,10),
得,解得,
∴
设直线OF为y=ax,代入F(4,8),
∴a=2,
∴y=2x,
联立直线OF、CG得,解得,
∴点P的坐标为(,).
【解析】【分析】(1)设AE=3x,则OE=5x,由勾股定理得AO=4x,则3x+2=4x,求出x即可求出点E的坐标,再由点E的坐标即可求出k的值;
(2)求出点D的坐标,证明△AOF∽△BFD,则∠AOF=∠BFD,得出∠OFD=180°-(∠AFO+∠BFD)=90°,即可得出结论;
(3)延长DF交y轴于点G,连接CG交OF于点P,则点P为所求作点,证明△AFG≌△BFD(AAS),得出OF为线段DG的垂直平分线,C(8,0),G(0,10),求出直线CG解析式,直线OF为y=ax,代入F(4,8),再联立方程组,即可求出点P的坐标。
一、选择题
1.已知、、为双曲线上的三个点,且,则以下判断正确的是( )
A.若,则 B.若,则
C.若,则 D.若,则
2.如图,的三个顶点的坐标分别为,,,将绕点顺时针旋转一定角度后使落在轴上,与此同时顶点恰好落在双曲线的图象上,则该反比例函数表达式为( )
A. B. C. D.
3.如图,平行四边形的顶点在双曲线上,顶点在双曲线上,中点恰好落在轴上,已知,则的值为( )
A.-8 B.-6 C.-4 D.-2
4.如图, 中, , ,点 在反比例函数 的图象上, 交反比例函数 的图象于点 ,且 ,则 的值为( )
A.-2 B.-4 C.-6 D.-8
5.如图,在平面直角坐标系中,菱形ABCO的顶点O在坐标原点,且与反比例函数y=的图象相交于A(m,3),C两点,已知点B(,),则k的值为( )
A.-6 B.-6 C.-12 D.-12
6.已知点A是双曲线y= 在第一象限分支上的一个动点,连接AO并延长交另一分支于点B,以AB为边作等边三角形ABC,点C在第四象限内,随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y= (x>0)上运动,则k的值是( )
A.3 B. C.﹣3 D.﹣
7.如图,点A是反比例图数y= (x<0)图象上一点,AC⊥x轴于点C,与反比例函数y= (x<0)图象交于点B,AB=2BC,连接OA、OB,若△OAB的面积为3,则m+n=( )
A.﹣4 B.﹣6 C.﹣8 D.﹣12
8.如图,点A是反比例函数y=(x<0)的图象上的一点,过点A作平行四边形ABCD,使点B、C在x轴上,点D在y轴上已知平行四边形ABCD的面积为6,则k的值为( )
A.6 B.-6 C.3 D.-3
9.如图,正方形ABCD位于第一象限,边长为3,点A在直线y=x上,点A的横坐标为1,正方形ABCD的边分别平行于x轴、y轴.若双曲线 与正方形ABCD有公共点,则k的取值范围为( )
A.1<k<9 B.2≤k≤34 C.1≤k≤16 D.4≤k<16
10.如图,在 轴正半轴上依次截取 ,过点 、 、 、…… 分别作 轴的垂线,与反比例函数 交于点 、 、 、…、 ,连接 、 、… ,过点 、 、…、 分别向 、 、…、 作垂线段,构成的一系列直角三角形(图中阴影部分)的面积和等于( ).
A. B. C. D.
二、填空题
11.已知过原点的一条直线与反比例函数的图象交于,两点在的右侧.是反比例函数图象上位于点上方的一动点,连接并延长交轴于点,连接交轴于点.若,则 .
12.如图,已知等边,顶点在双曲线上,点的坐标为.过作交双曲线于点,过作交轴于点,得到第二个等边;过作交双曲线于点,过作交轴于点,得到第三个等边;以此类推,…,则点的坐标为 .
13.如图,已知△P1OA1,△P2A1A2,△P3A2A3…△PnAn﹣1An都是等腰直角三角形,点P1、P2、P3…Pn都在函数y=(x>0)的图象上,斜边OA1、A1A2、A2A3…An﹣1An都在x轴上.则点A2021的坐标为 .
14.如图,将一块直角三角板OAB放在平面直角坐标系中,B(2,0),∠AOB=60°,点A在第一象限,过点A的双曲线为y= ,在x轴上取一点P,过点P作直线OA的垂线l,以直线l为对称轴,线段OB经轴对称变换后的像是O′B′.设P(t,0),当O′B′与双曲线有交点时,t的取值范围是 .
15.如图,在x轴正半轴上依次截取OA1=A1A2=A2A…An﹣1An(n为正整数),过点A1、A2、A3、…、An分别作x轴的垂线,与反比例函数y= (x>0)交于点P1、P2、P3、…、Pn,连接P1P2、P2P3、…、Pn﹣1Pn,过点P2、P3、…、Pn分别向P1A1、P2A2、…、Pn﹣1An﹣1作垂线段,构成的一系列直角三角形(见图中阴影部分)的面积和是
三、综合题
16.如图1,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点B在反比例函数y=(k>0)的第一象限内的图象上,OA=4,OC=3,动点P在y轴的右侧,且满足S△PCO=S矩形OABC.
(1)若点P在这个反比例函数的图象上,求点P的坐标;
(2)连接PO、PC,求PO+PC的最小值;
(3)若点Q是平面内一点,使得以B、C、P、Q为顶点的四边形是菱形,请你直接写出满足条件的所有点Q的坐标.
17.如图,平行四边形OABC的边OA在x轴的正半轴上,,,CD平分∠OCB,CD交OA于点D,作DE⊥CD交AB于点E,反比例函数的图象经过点C与点E.
(1)求k的值及直线CD的解析式;
(2)求证:;
(3)求点E的坐标.
18.已知一块矩形草坪的两边长分别是2米与3米,现在要把这个矩形按照如图1的方式扩大到面积为原来的2倍,设原矩形的一边加长a米,另一边长加长b米,可得a与b之间的函数关系式b=﹣2.某班“数学兴趣小组”对此函数进一步推广,得到更一般的函数y=﹣2,现对这个函数的图象和性质进行了探究,研究过程如下,请补充完整:
(1)类比反比例函数可知,函数y=﹣2的自变量x的取值范围是 ,这个函数值y的取值范围是 .
(2)“数学兴趣小组”进一步思考函数y=|﹣2|的图象和性质,请根据函数y=﹣2的图象,画出函数y=|﹣2|的图象;
(3)结合函数y=|﹣2|的图象解答下列问题:
①求出方程|﹣2|=0的根;
②如果方程|﹣2|=a有2个实数根,请直接写出a的取值范围.
19.已知点A(3,m+2),B(m+4,2)都在反比例函数y的图像上.
(1)求m,k的值;
(2)如图①,已知反比例函数y的图像上有两点P1(x1,y1),P2(x2,y2),且0<x1<x2<3,分别过P1,P2向x轴作垂线,垂足分别为M1,M2,过P1,P2向y轴作垂线,垂足分别为N1,N2.若记四边形P1M1ON1和四边形P2M2ON2的周长分别为C1,C2,试比较C1和C2的大小;并说明理由.
(3)如图②,若点B关于原点O对称点为C,点Q为双曲线AB段上任一动点,试探究∠ACQ与∠ABQ大小关系,并说明理由.
20.如图,四边形OABC为正方形,反比例函数的图象过AB上一点E,BE=2,.
(1)求k的值.
(2)反比例函数的图象与线段BC交于点D,直线y=ax+b过点D及线段AB的中点F,探究直线OF与直线DF的位置关系,并证明.
(3)点P是直线OF上一点,当PD+PC的值最小时,求点P的坐标.
1.【答案】D
【解析】【解答】解:A、∵y=-,若x1x2>0,
当x1<x2<x3<0时,
∴y3>y2>y1>0,
∴y1y3>0,
∴A选项错误,不符合题意;
B、∵y=-,若x1x3<0,
当x1<0<x2<x3时,
∴y1>0>y3>y2,
∴y1y2<0,
∴B选项错误,不符合题意;
C、∵y=-,若x2x3>0,
当x1<0<x2<x3时,
∴y1>0>y3>y2,
∴y1y3<0,
∴C选项错误,不符合题意;
D、∵y=-,若x2x3<0,
∴x1<x2<0<x3时,
∴y2>y1>0>y3,
∴y1y3<0,
∴D选项正确,符合题意.
故答案为:D.
【分析】根据反比例函数增减性,结合每个选项条件,求得对应y的正负号,再逐项进行分析判断即可.
2.【答案】D
【解析】【解答】解:,,,
轴,,,
,
将绕点顺时针旋转一定角度后使落在轴上,
,,,
在中,,
,
设,
①,②,
①②得③,
把③代入①整理得,解得(舍去),,
当时,,
,
把代入得.
∴,
故答案为:D.
【分析】利用A、B、C的坐标及勾股定理求出,由旋转的性质可得,,,在中,利用勾股定理求出OA',即得A’(0,8),设,可得①,②,联立①②可求出a、b值,即得C'坐标,将其代入中即可求出k值.
3.【答案】C
【解析】【解答】解:连接OB,过点B作BD⊥y轴于点D,过点C作CE⊥y于点E,
∵点P是BC的中点
∴PC=PB
∵
∴
∴
∵
∴
∵点B在双曲线上
∴
∴
∴
∴
∵点C在双曲线上
∴
∴.
故答案为:C.
【分析】连接OB,过点B作BD⊥y轴于点D,过点C作CE⊥y于点E,利用AAS证明△CPE≌△BPD,根据全等三角形的对应边相等得CE=BD,根据平行四边形的性质及同底等高的三角形面积相等得,根据反比例函数k的几何意义得,从而可得,最后再根据反比例函数k的几何意义结合图象所在的象限得出k的值.
4.【答案】D
【解析】【解答】解:过点A作AD⊥x轴,过点C作CE⊥x轴,过点B作BF⊥x轴
∴CE∥AD,∠CEO=∠BFO=90°
∵
∴∠COE+∠FOB=90°,∠ECO+∠COE=90°
∴∠ECO=∠FOB
∴△COE∽△OBF∽△AOD
又∵ ,
∴ ,
∴ ,
∴
∵点 在反比例函数 的图象上
∴
∴
∴ ,解得k=±8
又∵反比例函数位于第二象限,
∴k=-8
故答案为:D.
【分析】过点A作AD⊥x轴,过点C作CE⊥x轴,过点B作BF⊥x轴,由平行线的性质可得∠CEO=∠BFO=90°,根据同角的余角相等可得∠ECO=∠FOB,证明△COE∽△OBF∽△AOD,根据已知条件结合相似三角形的性质可得,根据反比例函数k的几何意义可得S△BOF=1,进而求出S△COE,再次利用反比例函数k的几何意义就可求出k的值.
5.【答案】A
【解析】【解答】解:作AE⊥x轴交x轴于点E,作CF⊥x轴交x轴于点F,作BD∥x轴交AE于点D,AB与y轴交点记为M;
∵四边形AOCB是菱形,
∴AB∥CO,AB=CO,
∴∠ABO=∠COB,
又∵BD∥x轴,
∴∠DBO=∠FOB,
∴∠ABD=∠COF,
∵AD⊥BD,CF⊥OF,
∴∠ADB=∠CFO=90°,
在△ADB和△CFO中,
,
∴△ADB≌△CFO(AAS),
∴AD=CF,
∵A(m,),B(,)
∴AD=,
∴CF=,
∵四边形AOCB是菱形,
∴∠AOB=∠COB,
∵B(,),
∴∠BOF=∠BOM=45°,
∵AE∥y轴,
∴∠EAO=∠AOM,
∴∠AOM=∠COF,
∴∠EAO=∠COF,
∵AE⊥x,CF⊥x轴,
∴∠AEO=∠CFO,
在△AEO和△OFC中,
∴△AEO≌△OFC(AAS),
∴OE=CF=,
∴点A的坐标为(,),
∵点A在反比例函数图象上,
∴ ,
解得:k=-6.
故答案为:A.
【分析】作AE⊥x轴交x轴于点E,作CF⊥x轴交x轴于点F,作BD∥x轴交AE于点D,AB与y轴交点记为M,由菱形的性质可得AB∥CO,AB=CO,根据平行线的性质可得∠ABO=∠COB,∠DBO=∠FOB,则
∠ABD=∠COF,证明△ADB≌△CFO,得到AD=CF,根据点A、B的坐标可得AD=CF=,证明△AEO≌△OFC,得到OE=CF=,则A(-,3),然后代入y=中就可求出k的值.
6.【答案】C
【解析】【解答】解:如图,连接OC,
根据反比例函数的中心对称性质,得 OA=OB,
∵△ABC是等边三角形,
∴OC⊥AB,∠OCA=30°,
∴OC:OA= ,
过点A作AD⊥x轴,垂足为点D,过点C作CE⊥x轴,垂足为点E,
∴∠ADO=∠OEC=90°,
∵∠AOD+∠OAD =90°,∠AOD+∠COE=90°,
∴∠OAD=∠COE,
∴△DOA∽△ECO,
∴EC:DO=OE:AD=OC:AD,
∴EC= DO,OE= AD,
设点A(a,b),则DO=a,AD=b,ab=1,
∵点C在第四象限,
∴点C的坐标为( b,- a),
∵点C始终在双曲线y= (x>0)上运动,
∴k=(- a)× b= -3ab= -3.
故答案为:C.
【分析】连接OC,则OA=OB,由等边三角形的性质可得OC⊥AB,∠OCA=30°,则OC:OA=,过点A作AD⊥x轴,垂足为点D,过点C作CE⊥x轴,垂足为点E,由同角的余角相等可得∠OAD=∠COE,证明△DOA∽△ECO,由相似三角形的性质表示出EC、OE,设点A(a,b),则DO=a,AD=b,ab=1,则点C的坐标为(b,-a),代入y=(x>0)中求解可得k的值.
7.【答案】D
【解析】【解答】解:∵AC⊥x轴于点C,与反比例函数y= (x<0)图象交于点B,
而m<0,n<0,
∴S△AOC= |m|=﹣ m,S△BOC= |n|=﹣ n,
∵AB=2BC,
∴S△ABO=2S△OBC=3,
即﹣ n= ,解得n=﹣3
∵﹣ m=3+ ,解得m=﹣9,
∴m+n=﹣9﹣3=﹣12.
故答案为:D.
【分析】利用反比例函数比例系数k的几何意义得到S△AOC= |m|=- m,S△BOC= |n|=- n,利用AB=2BC得到S△ABO=2S△OBC=3,所以- n= ,解得n=-3,再利用- m=3+ 得m=-9,然后计算m+n的值.
8.【答案】B
【解析】【解答】解:过点A作AE⊥BC,垂足为点E
∵四边形ABCD为平行四边形
∴AD∥x轴
∴四边形ADOE为矩形
∴平行四边形ABCD的面积=矩形ADOE的面积
∵矩形ADOE面积=|-k|,
∴|-k|=6
∵k<0
∴k=-6
故答案为:B.
【分析】过点A作AE⊥BC,垂足为点E,根据平行四边形的性质即可证明四边形ADOE为矩形,根据反比例函数的解析式k的含义即可得到答案。
9.【答案】C
【解析】【解答】解:点A在直线y=x上,其中A点的横坐标为1,则把x=1代入y=x解得y=1,则A的坐标是(1,1),∵AB=BC=3,∴C点的坐标是(4,4),∴当双曲线 经过点(1,1)时,k=1;当双曲线 经过点(4,4)时,k=16,因而1≤k≤16.
故答案为:C.
【分析】先求出点A的坐标,再求出点C的坐标,分别求出双曲线经过点A和点C时的k的值,即可求出k的取值范围.
10.【答案】B
【解析】【解答】∵
∴设 (1, ), (1, ), (1, )… (1, )
∵ 、 、 、…、 在反比例函数 的图像上
∴
∴
∴
∵
∴
…
∴
因此答案选择B.
【分析】由 可设 点的坐标为(1, ), 点的坐标为(1, ), 点的坐标为(1, )… 点的坐标为(1, ),把x=1,x=2,x=3代入反比例函数的解析式即可求出 的值,再由三角形的面积公式可以得出 … 的值,即可得出答案.
11.【答案】2
【解析】【解答】解:如图所示,过点分别作轴的垂线,垂足分别为,
,
,
,
则,
根据对称性可得
∴
故答案为:2.
【分析】过点A、B、C分别作y轴的垂线,垂足分别为F、G、H,则CF∥AG∥BH,证明△DFC∽△DGA,△FCE∽△HBE,根据相似三角形的性质可得BH=(n-1)CF,根据平行线分线段成比例的性质可得AG=(m+1)CF,根据对称性可得BH=AG=(m+1)CF,联立化简可得m与n的关系.
12.【答案】(,0)
【解析】【解答】解:如图,作A2C⊥x轴于点C,设B1C=a,则A2C=,
OC=OB1+B1C=2+a,A2(2+a,).
∵点A2在双曲线上,
∴(2+a) =,
解得a=-1,或a=--1(舍去),
∴OB2=OB1+2B1C=2+2-2=2,
∴点B2的坐标为(2,0);
作A3D⊥x轴于点D,设B2D=b,则A3D=b,
OD=OB2+B2D=2+b,A2(2+b,b).
∵点A3在在双曲线上,
∴(2+b) b=,
解得b=-+,或b=--(舍去),
∴OB3=OB2+2B2D=2-2+2=2,
∴点B3的坐标为(2,0);
同理可得点B4的坐标为(2,0)即(4,0);
以此类推…,
∴点Bn的坐标为(2,0),
当n=12时,2
∴点B12的坐标为(4,0),
故答案为(4,0).
【分析】如图,作A2C⊥x轴于点C,根据等边三角形及反比例函数图象上点的坐标特征分别求出B1、B2、B3、B4的坐标,从而得出规律点Bn的坐标为(2,0),继而求出B12的坐标即可.
13.【答案】(,0)
【解析】【解答】解:可设点P1(x,y),
根据等腰直角三角形的性质可得:x=y,
又∵y=,
则x2=4,
∴x=±2(负值舍去),
再根据等腰三角形的三线合一,得A1的坐标是(4,0),
设点P2的坐标是(4+y,y),
又∵y=,则y(4+y)=4,即y2+4y-4=0
解得,y1=-2+2,y2=-2-2,
∵y>0,
∴y=2-2,
再根据等腰三角形的三线合一,得A2的坐标是(4,0);
可以再进一步求得点A3的坐标是(4,0),推而广之,则An点的坐标是(4,0).
故点A2021的坐标为 (4,0).
故答案是:(4,0).
【分析】先根据等腰直角三角形的性质得出P1的横、纵坐标相等,再结合双曲线的解析式得出P1的坐标,则根据等腰三角形的三线合一求得A1的坐标,同样根据等腰直角三角形的性质、点A1的坐标和双曲线的解析式求得A2的坐标,根据A1、A2的坐标特征即可发现其规律。
14.【答案】4≤t≤2 或﹣2 ≤t≤﹣4
【解析】【解答】解:当点O′与点A重合时,
∵∠AOB=60°,过点P作直线OA的垂线l,以直线l为对称轴,线段OB经轴对称变换后是O′B′,AP=OP,
∴△AOP′是等边三角形,
∵B(2,0),
∴BO=BP′=2,
∴点P的坐标是(4,0),
即当P的坐标是(4,0)时,直线O B 与双曲线有交点O′;
当B′在双曲线上时,作B′C⊥OP于C,
∵BP=B′P,∠B′BP=60°,
∴△BB′P是等边三角形,
∴BP=B′P=t﹣2,
∴CP= (t﹣2),B′C= (t﹣2),
∴OC=OP﹣CP= t+1,
∴B′的坐标是( t+1, (t﹣2)),
∵∠ABO=90°,∠AOB=60°,OB=2,
∴OA=4,AB=2 ,
∴A(2,2 ),
∵A和B′都在双曲线上,
∴( t+1) (t﹣2))=2×2 ,
解得:t=±2 ,
∴t的取值范围是4≤t≤2 或﹣2 ≤t≤﹣4.
故答案为:4≤t≤2 或﹣2 ≤t≤﹣4.
【分析】当点O'与点A重合时,过点P作直线OA的垂线l,以直线l为对称轴,线段OB经轴对称变换后是O′B′,得出AP=OP,结合∠AOB=60°,得出△AOP是等边三角形,根据等边三角形的性质求出点P的坐标,进一步解直角△AOB,根据A和B′都在双曲线上,建立关于t的代数式求解,即可得出t的范围.
15.【答案】
【解析】【解答】设OA1=A1A2=A2A3=…=An﹣1An=1,
∴P1(1,y1),P2(2,y2),P3(3,y3),…Pn(n,yn),
∵P1,P2,P3…Pn在反比例函数y= (x>0)的图象上,
∴y1=1,y2= ,y3= …yn= ,
∴S1= ×1×(y1﹣y2)= ×(1﹣ ),
S2= ×1×(y2﹣y3)= ×( ﹣ ),
S3= ×1×(y3﹣y4)= ×( ﹣ ),
…
Sn﹣1= ( ﹣ ),
∴S1+S2+S3+…+Sn﹣1═ (1﹣ + ﹣ + ﹣ +…+ ﹣ )= .
故答案为: .
【分析】设OA1=A1A2=A2A3=…=An﹣1An=1,得出P1(1,y1),P2(2,y2),P3(3,y3),…Pn(n,yn),再根据P1,P2,P3…Pn在反比例函数y= (x>0)的图象上,得出y1=1,y2= ,y3= …yn= ,推出S1的的答案,从而得出S2、S3、…,从而得出Sn﹣1= ( ﹣ ),即可得出答案。
16.【答案】(1)解:∵四边形OABC是矩形,OA=4,OC=3,
∴点B的坐标为(4,3),
∵点B在反比例函数的第一象限内的图象上
∴k=12,
∴反比例函数解析式为y=,
设点P的横坐标为m(m>0),
∵.
∴,
∴,
当点,P在这个反比例函数图象上时,则 ,
∴点P的坐标为(3,4).
(2)解:取点F(6,0),连接FP,CF,
∴O、F关于直线对称,
由(1)知,点P的横坐标为3,
∴点P在直线上,
∴PF=PO,
∴PC+PO=PF+PC,
∴当C、P、F三点共线时,PF+PC即PC+PO有最小值,最小值即为CF,
∴PO+PC的最小值=PF+PC=CF=;
(3)解:或或或
【解析】【解答】(3)解:设点Q的坐标为(m,n),点P的坐标为(3,t)
如图3-1所示,当BP为以B、C、P、Q为顶点的四边形的边时,由菱形的性质可知PB=BC=4,
∴,
∴或,
∴点P的坐标为或,
∴点Q的坐标为或;
如图3-2所示,当BP为以B、C、P、Q为顶点的四边形的对角线时,由菱形的性质可知PC=BC=4,
∴,
∴或,
∴点P的坐标为或,
∴同理可得点Q的坐标为或;
综上所述,点Q的坐标为或或或
【分析】(1)先确定点B坐标,从而确定反比例函数解析式,设点P的横坐标为m(m>0), 根据 构建方程求出m值,即得点P坐标;
(2)取点F(6,0),连接FP,CF, 即得O、F关于直线对称, 由(1)可推出点P在直线x=3上,可得PF=PO,即得PC+PO=PF+PC,当C、P、F三点共线时,PF+PC即PC+PO有最小值,最小值即为CF,利用勾股定理求出CF的长即可;
(3)分两种情况:①当BP为以B、C、P、Q为顶点的四边形的边时,②当BP为以B、C、P、Q为顶点的四边形的对角线时,根据菱形的性质分别求解即可.
17.【答案】(1)解:如图1,过C点作CH垂直x轴,
∵,,
∴,
∴,,
∴点,
∴反比例函数的系数,
∵在平行四边形OABC,,
∴,
又∵CD平分∠OCB,
∴,
∴是等边三角形,
∴,即点D,
∵点C,点D,
∴直线的解析式是
(2)证明:∵是等边三角形,
∴,
又∵DE⊥CD,
∴,
∵,
∴,
∴,
∴.
(3)解:过E点作EQ垂直x轴,设,
∵,
∴,,
∴点
点在反比例函数的图象上,
∴
∴或(舍去),则点的坐标是)
【解析】【分析】(1)过C点作CH垂直x轴,利用解直角三角形求出点C坐标,再利用带动系数法求出值;先证△OCD是等边三角形,可得OD=OC=12,即得D(12,0),利用待定系数法求出直线CD解析式即可;
(2)由等边三角形的性质可得∠CDO=60°,从而推出, 利用等腰三角形的性质即得结论;
(3)过E点作EQ垂直x轴,设, 可得,, 即点,将点E坐标代入反比例函数解析式中即可求解.
18.【答案】(1)x≠﹣3;y≠﹣2
(2)解:函数y=|﹣2|的图象,如图所示:
(3)解:①方程|﹣2|=0该方程的根是x=3;
②如果方程|﹣2|=a有2个实数根,则a的取值范围是0<a<2或a>2.
【解析】【解答】解:(1)y=﹣2的自变量x的取值范围是x≠﹣3,这个函数值y的取值范围是y≠﹣2,
故答案为:x≠﹣3;y≠﹣2.
【分析】(1)根据分式有意义的条件得出自变量x的取值范围是x≠-3,根据≠0,得出函数值y的取值范围是y≠-2,即可得出答案;
(2)y=﹣2的图象的x轴上方部分沿x轴翻折,即可得出函数y=|﹣2|的图象;
(3)①利用图象法即可得出方程|﹣2|=0该方程的根是x=3;
②利用图象法即可得出a的取值范围是0<a<2或a>2.
19.【答案】(1)解:∵点A(3,m+2),B(m+4,2)都在反比例函数 y= 的图象上.
∴3(m+2)= 2(m+4),∴解得:m=2.
∴A(3,4)、B(6,2).∴k=12;
(2)解: ,
∵∴
∴
∴ .
(3)解:∠ACQ=∠ABQ理由:
设AC 、QC分别交x轴于D、G两点,延长AB、QB分别x轴于E、F两点,
分别求出直线AB、直线AC的解析式为: 、 ,
得到:E(9,0)、D(-3,0)
作AH⊥DF于H,则DH=EH=6,
∴AD=AE ,∠ADE=∠AED
设Q( ),直线BQ的解析式为:
将点B(6,2)、Q( )代入,得:
解得:
∴直线BQ的解析式为:
当 时,
∴
同理可得:直线CQ的解析式为: ,
作QI⊥x轴
∵IG=n-(n-6)=6,IF=n+6-n=6
∴IG=IF
∴∠QGF=∠F
∵∠ADE=∠ACQ+∠DGC=∠ACQ+∠QGF
∠AED=∠F+∠EBF=∠F+∠ABQ
∴∠ACQ+∠QGF=∠F+∠ABQ
∴∠ACQ=∠ABQ
【解析】【分析】(1)根据 点A(3,m+2),B(m+4,2)都在反比例函数y的图像上 ,将点A,B的坐标分别代入反比例函数,得到关于m的一元一次方程,解方程求出m的值,再将m代入点A,B中,代入其中一个点即可求k;
(2)根据矩形的周长公式()和反比例函数解析式分别表示出两个四边形的周长,然后作差得,根据题意 0<x1<x2<3,可得,进而可判断;
(3)设AC 、QC分别交x轴于D、G两点,延长AB、QB分别x轴于E、F两点,利用待定系数法分别求出直线AB、直线AC的解析式为: 、 ,得到:E(9,0)、D(-3,0),作AH⊥DF于H,则DH=EH=6,根据等腰三角形的判定(高线、中线为同一条直线的三角形是等腰三角形)可得AD=AE ,∠ADE=∠AED,设Q( ),直线BQ的解析式为: ,代入点B和点Q的坐标,得到直线BQ的解析式为: ,进而得出点F的坐标,同理可得:直线CQ的解析式为: , ,作QI⊥x轴,可得IG=IF,根据等边对等角得到∠QGF=∠F,利用三角形的外角性质(三角形的外角等于与它不相邻的两个内角的和)和等量代换即可得到∠ACQ=∠ABQ..
20.【答案】(1)解:∵四边形OABC是正方形,
∴AO=AB,∠OAB=90°,
∵,
设AE=3x,则OE=5x,由勾股定理得AO=4x,
∴3x+2=4x,
∴x=2,
∴AE=3x=6,AO=4x=8,
∴点E坐标为(6,8),
∴k=6×8=48;
(2)解:OF⊥DF,理由如下:
将x=8代入y=得y=6,
∴D(8,6),
∴BD=BC-CD=8-6=2,
∵点F是线段AB的中点,
∴AF=BF=4,
∵,∠OAF=∠FBD=90°,
∴△AOF∽△BFD,
∴∠AOF=∠BFD,
∴∠AFO+∠BFD=∠AFO+∠AOF=90°,
∴∠OFD=180°-(∠AFO+∠BFD)=90°,
∴OF⊥DF;
(3)解:延长DF交y轴于点G,连接CG交OF于点P,则点P为所求作点,
∵四边形OABC为正方形,∠AFG=∠BFD,AF=BF,
∴△AFG≌△BFD(AAS),
∴AG=BD=2,GF=DF,
由(2)得OF⊥DF,
∴OF为线段DG的垂直平分线,
∴PD+PC的最小值=PG+PC=CG,
∵OC=OA=8,
∴C(8,0),G(0,10),
设直线CG解析式为y=mx+n,代入C(8,0),G(0,10),
得,解得,
∴
设直线OF为y=ax,代入F(4,8),
∴a=2,
∴y=2x,
联立直线OF、CG得,解得,
∴点P的坐标为(,).
【解析】【分析】(1)设AE=3x,则OE=5x,由勾股定理得AO=4x,则3x+2=4x,求出x即可求出点E的坐标,再由点E的坐标即可求出k的值;
(2)求出点D的坐标,证明△AOF∽△BFD,则∠AOF=∠BFD,得出∠OFD=180°-(∠AFO+∠BFD)=90°,即可得出结论;
(3)延长DF交y轴于点G,连接CG交OF于点P,则点P为所求作点,证明△AFG≌△BFD(AAS),得出OF为线段DG的垂直平分线,C(8,0),G(0,10),求出直线CG解析式,直线OF为y=ax,代入F(4,8),再联立方程组,即可求出点P的坐标。
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
