6.3反比例函数的应用同步练习(培优版)(含解析)北师大版数学九年级上册
文档属性
| 名称 | 6.3反比例函数的应用同步练习(培优版)(含解析)北师大版数学九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 534.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-27 16:20:26 | ||
图片预览

文档简介
6.3反比例函数的应用(培优版)
一、选择题
1.如图是反比例函数和(为常数)在第一象限内的图象,点M在的图象上,轴于点C,交的图象于点A,轴于点D,交的图象于点B,当点M在的图象上运动时,以下结论:①与的面积相等;②四边形的面积不变;③当点A是的中点时,则点B是的中点.其中错误结论的个数是( )
A.0 B.1 C.2 D.3
2.如图,已知点,,是轴上位于点上方的一点,平分,平分,直线交于点.若反比例函数的图像经过点,则的值是( )
A.-8 B.-9 C.-10 D.-12
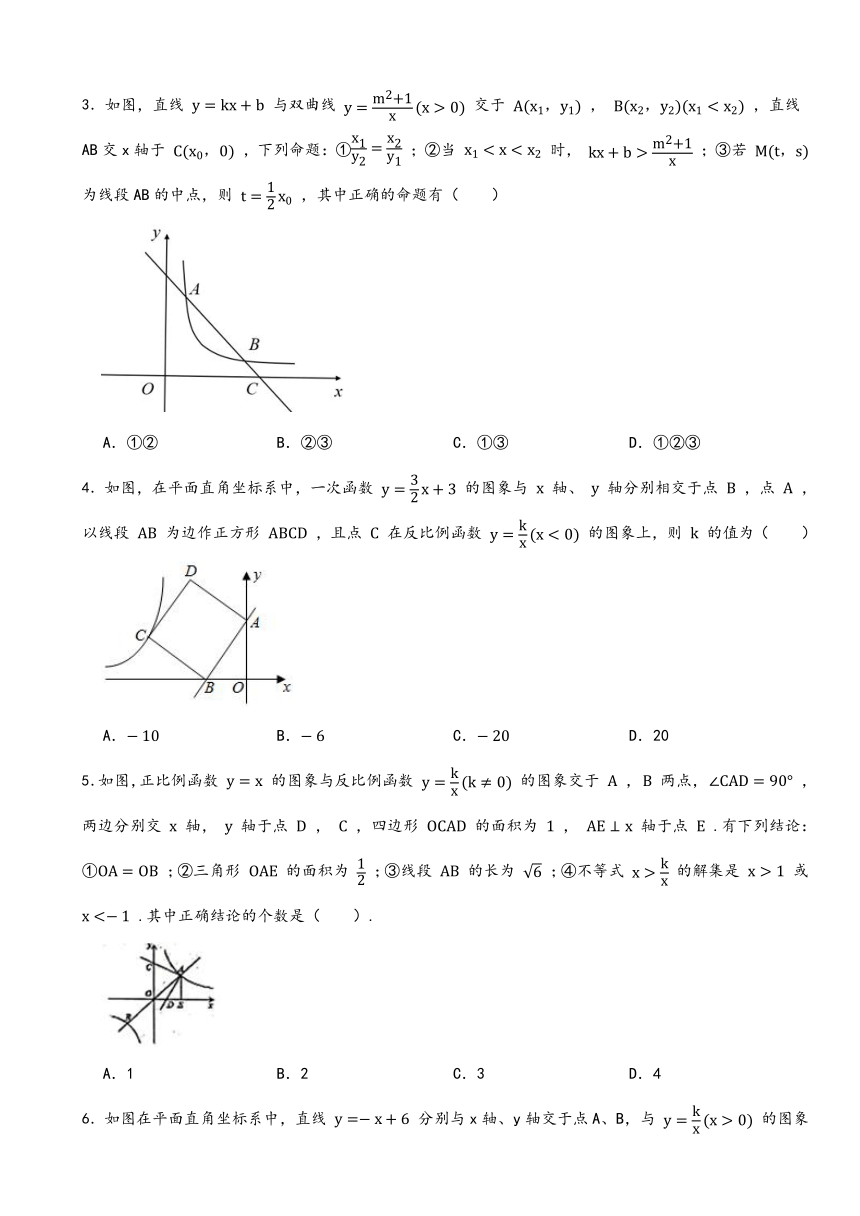
3.如图,直线 与双曲线 交于 , ,直线AB交x轴于 ,下列命题:① ;②当 时, ;③若 为线段AB的中点,则 ,其中正确的命题有( )
A.①② B.②③ C.①③ D.①②③
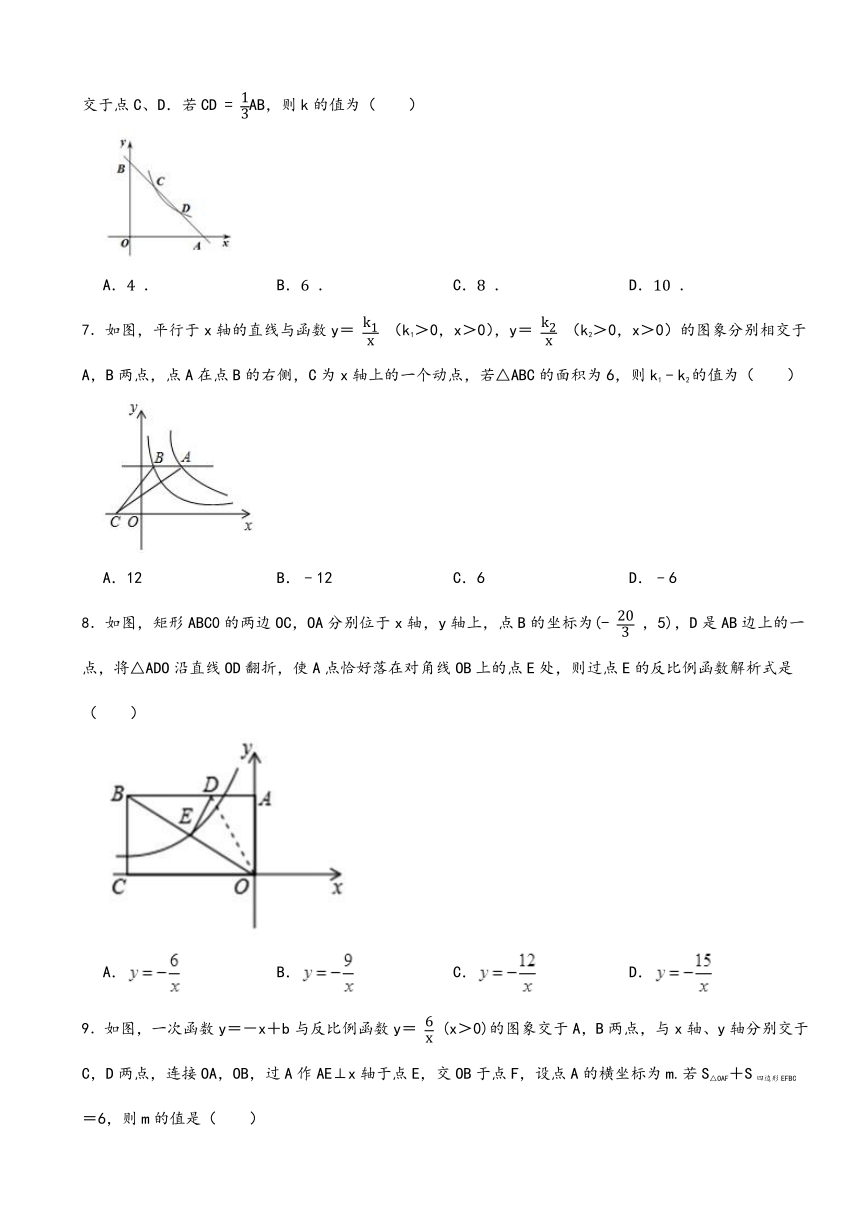
4.如图,在平面直角坐标系中,一次函数 的图象与 轴、 轴分别相交于点 ,点 ,以线段 为边作正方形 ,且点 在反比例函数 的图象上,则 的值为( )
A. B. C. D.20
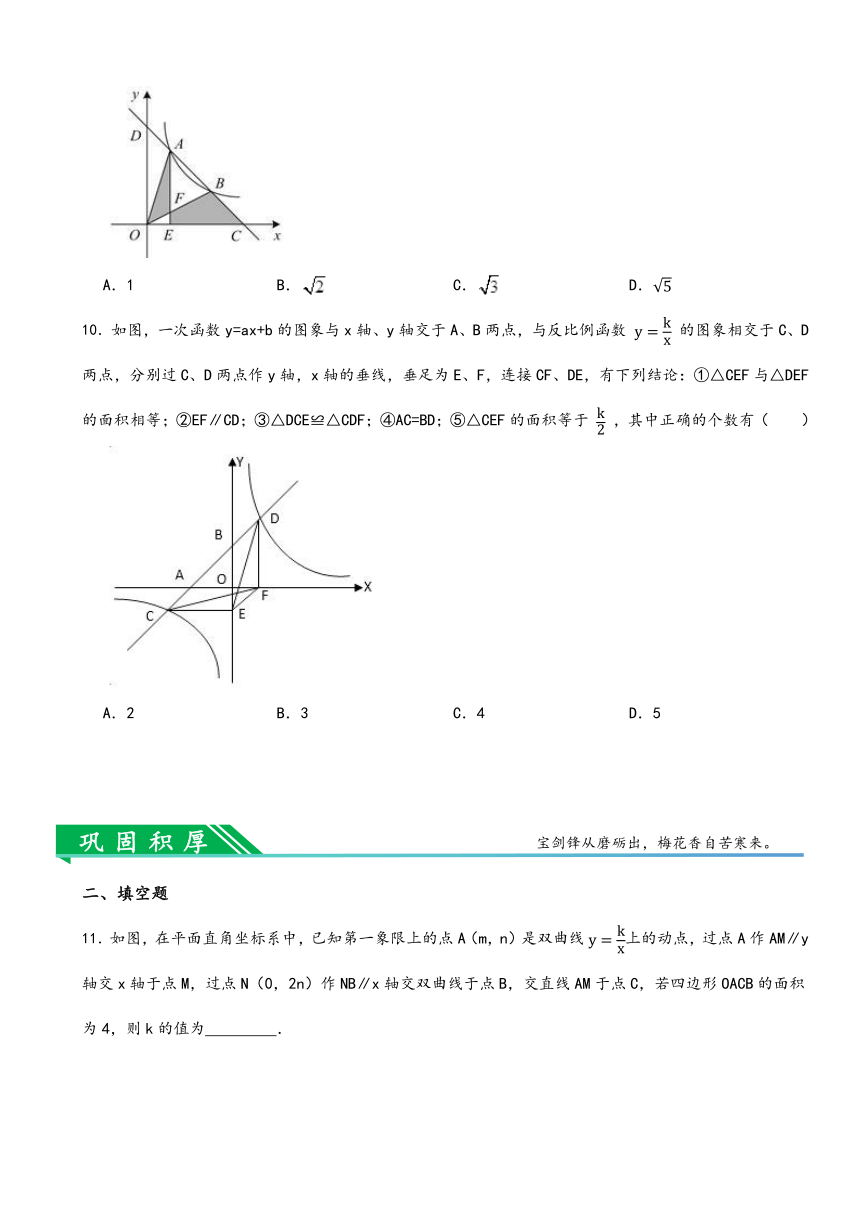
5.如图,正比例函数 的图象与反比例函数 的图象交于 , 两点, ,两边分别交 轴, 轴于点 , ,四边形 的面积为 , 轴于点 .有下列结论:① ;②三角形 的面积为 ;③线段 的长为 ;④不等式 的解集是 或 .其中正确结论的个数是( ).
A.1 B.2 C.3 D.4
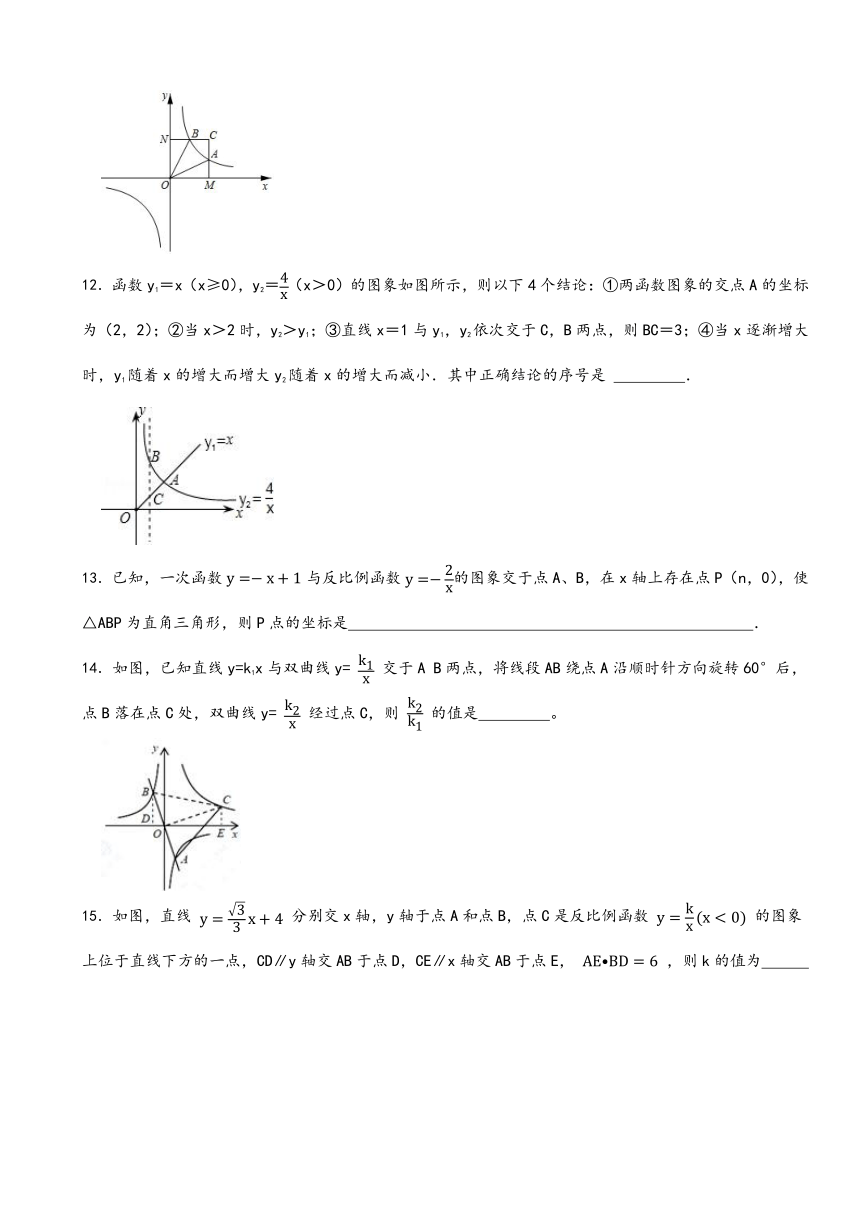
6.如图在平面直角坐标系中,直线 分别与x轴、y轴交于点A、B,与 的图象交于点C、D.若CD = AB,则k的值为( )
A. . B. . C. . D. .
7.如图,平行于x轴的直线与函数y= (k1>0,x>0),y= (k2>0,x>0)的图象分别相交于A,B两点,点A在点B的右侧,C为x轴上的一个动点,若△ABC的面积为6,则k1﹣k2的值为( )
A.12 B.﹣12 C.6 D.﹣6
8.如图,矩形ABC0的两边OC,OA分别位于x轴,y轴上,点B的坐标为(- ,5),D是AB边上的一点,将△ADO沿直线OD翻折,使A点恰好落在对角线OB上的点E处,则过点E的反比例函数解析式是( )
A. B. C. D.
9.如图,一次函数y=-x+b与反比例函数y= (x>0)的图象交于A,B两点,与x轴、y轴分别交于C,D两点,连接OA,OB,过A作AE⊥x轴于点E,交OB于点F,设点A的横坐标为m.若S△OAF+S四边形EFBC=6,则m的值是( )
A.1 B. C. D.
10.如图,一次函数y=ax+b的图象与x轴、y轴交于A、B两点,与反比例函数 的图象相交于C、D两点,分别过C、D两点作y轴,x轴的垂线,垂足为E、F,连接CF、DE,有下列结论:①△CEF与△DEF的面积相等;②EF∥CD;③△DCE≌△CDF;④AC=BD;⑤△CEF的面积等于 ,其中正确的个数有( )
A.2 B.3 C.4 D.5
二、填空题
11.如图,在平面直角坐标系中,已知第一象限上的点A(m,n)是双曲线上的动点,过点A作AM∥y轴交x轴于点M,过点N(0,2n)作NB∥x轴交双曲线于点B,交直线AM于点C,若四边形OACB的面积为4,则k的值为 .
12.函数y1=x(x≥0),y2=(x>0)的图象如图所示,则以下4个结论:①两函数图象的交点A的坐标为(2,2);②当x>2时,y2>y1;③直线x=1与y1,y2依次交于C,B两点,则BC=3;④当x逐渐增大时,y1随着x的增大而增大y2随着x的增大而减小.其中正确结论的序号是 .
13.已知,一次函数与反比例函数的图象交于点A、B,在x轴上存在点P(n,0),使△ABP为直角三角形,则P点的坐标是 .
14.如图,已知直线y=k1x与双曲线y= 交于A B两点,将线段AB绕点A沿顺时针方向旋转60°后,点B落在点C处,双曲线y= 经过点C,则 的值是 。
15.如图,直线 分别交x轴,y轴于点A和点B,点C是反比例函数 的图象上位于直线下方的一点,CD∥y轴交AB于点D,CE∥x轴交AB于点E, ,则k的值为
三、综合题
16.反比例函数的图象与直线交点为、,点在点的左侧.
(1)如图1,求反比例函数和一次函数的解析式;
(2)如图2,点是反比例函数()上一点,点是平面内一点,连接,、,若四边形是矩形,求点的坐标;
(3)如图3,点是轴上一点,以为边向线段右侧作等边,若点在第四象限且到轴的距离是,求点的坐标.
17.新冠疫情期间,口罩的需求量增大,某口罩加工厂承揽生产1600万个口罩的任务,每天生产的口罩数量相同,计划用x天(x>4)完成.
(1)求每天生产口罩y(万个)与生产时间x(天)之间的函数表达式;
(2)由于疫情形势严峻,卫生管理部门要求厂家提前4天交货,那么加工厂每天要多做20万个口罩才能完成任务,求实际生产时间.
18.制作一种产品,需先将材料加热达到60℃后,再进行操作,设该材料温度为y(℃)从加热开始计算的时间为x(min).据了解,当该材料加热时,温度y与时间x成一次函数关系:停止加热进行操作时,温度y与时间x成反比例关系(如图).已知在操作加热前的温度为15℃,加热5分钟后温度达到60℃.
(1)分别求出将材料加热和停止加热进行操作时,y与x的函数关系式;
(2)根据工艺要求,当材料的温度低于15℃时,须停止操作,那么从开始加热到停止操作,共经历了多少时间?
19.列出下列问题中的函数关系式,并判断它们是否为反比例函数.
(1)某农场的粮食总产量为1 500t,则该农场人数y(人)与平均每人占有粮食量x(t)的函数关系式;
(2)在加油站,加油机显示器上显示的某一种油的单价为每升4.75元,总价从0元开始随着加油量的变化而变化,则总价y(元)与加油量x(L)的函数关系式;
(3)小明完成100m赛跑时,时间t(s)与他跑步的平均速度v(m/s)之间的函数关系式.
20.在工程实施过程中,某工程队接受一项开挖水渠的工程,所需天数y(天)与每天完成工程量x(米)是反比例函数关系,图象如图所示:
(1)求y与x之间的函数关系式
(2)若该工程队有4台挖掘机,每台挖掘机每天能够开挖水渠30米,问该工程队需要用多少天才能完成此项任务
1.【答案】A
【解析】【解答】∵点A、B在同一反比例函数的图像上,
∴.
故①符合题意;
∵点M在反比例函数的图象上,
∴.
∵,
∴.
故②符合题意;
连接,可知.
∵点A是的中点,
∴.
∵,
∴,
∴点B是的中点.
故③符合题意.
所以错误的个数是0.
故答案为:A.
【分析】利用反比例函数图象上的点坐标的特征和反比例函数k的几何意义逐项判断即可。
2.【答案】B
【解析】【解答】如图,过分别作的垂线,垂足分别为,,
平分,平分,
,
,
,
四边形是正方形
,,
故答案为:B
【分析】利用全等三角形的判定与性质,勾股定理,结合函数图象求解即可。
3.【答案】D
【解析】【解答】解:∵点A(x1,y1),B(x2,y2)在双曲线 上,
∴x1y1=x2y2=m2+1,
∴ ,①符合题意;
∵当x1<x<x2时,直线y=kx+b在双曲线 上方,
∴当 时, ,②符合题意;
∵M(t,s)为线段AB的中点,
∴ ,
当 时,
即 ,
此时, ,
∴ ,
把C(x0,0)代入y=kx+b得kx0+b=0,
解得 ,
∴x1+x2=x0,
∴ ,所以③符合题意.
故答案为:D.
【分析】根据反比例函数上的点横纵坐标之积相等,可得x1y1=x2y2,整理即可判断①;
结合函数图象一次函数在反比例函数上的的部分可对②进行判断;
根据线段的中点公式可得 ,联立反比例函数和一次函数整理后得一元二次方程 ,根据根与系数关系可得 ,由此可得 ,由一次函数与x轴的交点可得 ,由此可判断③.
4.【答案】A
【解析】【解答】解:∵一次函数 中,当x=0时,y=0+3=3,
∴A(0,3),
∴OA=3;
∵当y=0时,0= ,
∴x= 2,
∴B( 2,0),
∴OB=2;
过点C作CE⊥x轴于E,
∵四边形ABCD是正方形,
∴∠ABC=90°,AB=BC,
∵∠CBE+∠ABO=90°,∠BAO+∠ABO=90°,
∴∠CBE=∠BAO.
在△AOB和△BEC中, ,
∴△AOB≌△BEC(AAS),
∴BE=AO=3,CE=OB=2,
∴OE=2+3=5,
∴C点坐标为(-5,2),
∵点C在反比例函数 (x<0)图象上,
∴k= 5×2= 10.
故答案为:A.
【分析】过点C作CE⊥x轴于E,证明△AOB≌△BEC,可得点C坐标,代入求解即可.
5.【答案】B
【解析】【解答】解:∵正比例函数 的图象与反比例函数 的图象交于 , 两点
∴
∴
∴
结合题意,得 ,
∴ ,
∴ ,故①正确;
设点C坐标为 ,设点D坐标为 ,结合题意, 且
∴ ,
∵四边形 的面积为
∴四边形 的面积
∴
结合题意, ,
又∵ ,且
∴
∴
∴
∴
∴
∴ , , ,故③错误;
∵
∴ ,
∴
∴ ,故②正确;
当 时, 即
∴
∴ 或 (舍去)
当 时, 即
∴
∴
∴不等式 的解集是 或 ,故④错误;
故答案为:B.
【分析】根据正比例函数 的图象与反比例函数 的图象的性质,结合题意,可计算得 ;根据 和四边形 的面积为 ,设点C坐标为 ,设点D坐标为 ,通过勾股定理和四边形面积解方程,即可得到k的值,从而计算得 和三角形 的面积,以及不等式 的解集.
6.【答案】C
【解析】【解答】解:对直线y=﹣x+6,令x=0,则y=6,令y=0,则x=6,
∴点A、B的坐标分别为(6,0)、(0,6),
∴OB=OA=6,
∴AB=6 =3CD,∠BAO=45°,
∴ ,
联立y=﹣x+6和y= 并整理得:x2﹣6x+k=0,
设点C、D的横坐标分别为a,b,则a+b=6,ab=k,
∵∠BAO=45°,
∴CD= ,
∴CD2=2(a﹣b)2=2[(a+b)2﹣4ab]=2(36﹣4k)=(2 )2,解得:k=8.
故答案为:C.
【分析】先求出点A、B的坐标,于是可得AB的长,进而可得CD的长,设C、D的横坐标分别为a,b,则a,b是联立y=﹣x+6和y= 并整理后的方程的解,由CD= 并结合根与系数的关系可得关于k的方程,解方程即可求出k,从而可得答案.
7.【答案】A
【解析】【解答】解:设:A、B点的坐标分别是A( ,m)、B( ,m),
则:△ABC的面积= AB yA= ( ﹣ ) m=6,
则k1﹣k2=12.
故答案为:A.
【分析】△ABC的面积= AB yA,先设A、B两点坐标(其y坐标相同),然后计算相应线段长度,用面积公式即可求解.
8.【答案】C
【解析】【解答】解:过E作EF⊥OC交OC于点F,如图:
∵矩形ABCO中,
∴BC⊥OC,
∵EF⊥OC,
∴EF∥BC,
∴△OEF∽△OBC,
∴,
∵B(-,5),
∴BC=5,OC=-,
即=,
∴令EF=3x,OF=4x,
根据翻折的性质可知OA=OE=BC=5,
在Rt△OEF中,
∴(3x)2+(4x)2=52,
解得:x=1,
∴EF=3,OF=4,
∴E(-4,3),
设经过点E的反比例函数解析式为:y=,
又∵点E(-4,3)在反比例函数上,
∴k=-4×3=-12,
∴经过点E的反比例函数解析式为:y=.
故答案为:C.
【分析】解:过E作EF⊥OC交OC于点F,如图:
∵矩形ABCO中,
∴BC⊥OC,
∵EF⊥OC,
∴EF∥BC,
∴△OEF∽△OBC,
∴,
∵B(-,5),
∴BC=5,OC=-,
即=,
∴令EF=3x,OF=4x,
根据翻折的性质可知OA=OE=BC=5,
在Rt△OEF中,
∴(3x)2+(4x)2=52,
解得:x=1,
∴EF=3,OF=4,
∴E(-4,3),
设经过点E的反比例函数解析式为:y=,
又∵点E(-4,3)在反比例函数上,
∴k=-4×3=-12,
∴经过点E的反比例函数解析式为:y=.
故答案为:C.
【分析】过E作EF⊥OC交OC于点F,根据矩形的性质和相似三角形的判定得△OEF∽△OBC,由相似三角形的性质得=,从而令EF=3x,OF=4x,几何翻折的性质可知OE=5,在Rt△OEF中,根据勾股定理列出方程,解之得出x值,从而可得E点坐标,根据待定系数法即可求得经过点E的反比例函数解析式.
9.【答案】C
【解析】【解答】解:∵A点在反比例函数y=(x>0),且A点横坐标为m,
∴A(m,),
又∵A点在一次函数y=-x+b上,
∴A(m,-m+b),
∴=-m+b,
即b=m+,
作AM⊥OD于M,BN⊥OC于N,如图:
∵反比例函数y=与一次函数y=-x+b均关于直线y=x对称,
∴AD=BC,OD=OC,DM=AM=BN=CN,
设S△AOF=s,
则S△OEF=3-s,S四边形EFBC=6-s,S△OBC=S△OAD=9-2s,S△ADM=6-2s=2(3-s),
∴S△ADM=2S△OEF,
由对称性可知:AD=BC,OD,∠ODC=∠OCD=45°,
∴△AOM≌△BON,
∵AM=BN=DM=CN,
∴EF=AM=BN,
∴EF是△BON的中位线,
∴N(2m,0),
∴B(2m,),
又∵点B在一次函数y=-x+b上,
∴=-2m+m+,
整理得:m2=3,
∵m>0,
∴m=.
故答案为:C.
【分析】由A是反比例函数与一次函数的交点得 =-m+b,即b=m+,作AM⊥OD于M,BN⊥OC于N,设S△AOF=s,则S△OEF=2-s,S四边形EFBC=4-s,S△OBC=S△OAD=6-2s,S△ADM=4-2s=2(2-s), 从而得S△ADM=2S△OEF,根据对称性和全等三角形的性质可得 EF是△BON的中位线,由此得B(2m,),将点B坐标代入一次函数解析式即可求得m值.
10.【答案】C
【解析】【解答】解:设点D的坐标为(x,kx),则F(x,0).
由函数的图象可知:x>0,k>0. ∴S△DFE= DF OF= |xD| | |= k,
同理可得S△CEF= k,故⑤正确; 故S△DEF=S△CEF.故①正确;
若两个三角形以EF为底,则EF边上的高相等,故CD∥EF.故②正确;
③条件不足,无法得到判定两三角形全等的条件,故③错误;
④法一:∵CD∥EF,DF∥BE,
∴四边形DBEF是平行四边形,
∴S△DEF=S△BED, 同理可得S△ACF=S△ECF;
由①得:S△DBE=S△ACF. 又∵CD∥EF,BD、AC边上的高相等,
∴BD=AC,故④正确;
法2:∵四边形ACEF,四边形BDEF都是平行四边形, 而且EF是公共边, 即AC=EF=BD,
∴BD=AC,故④正确; 因此正确的结论有4个:①②④⑤.
故答案为:C.
【分析】此题要根据反比例函数的性质进行求解,解决此题的关键是要证出CD∥EF,可从①问的面积相等入手;△DFE中,以DF为底,OF为高,可得S△DFE=|xD| |yD|=k,同理可求得△CEF的面积也是k,因此两者的面积相等;若两个三角形都以EF为底,那么它们的高相同,即E、F到AD的距离相等,由此可证得CD∥EF,然后根据这个条件来逐一判断各选项的正误.
11.【答案】4
【解析】【解答】解:∵AM∥y轴,NB∥x轴,
∴四边形ONCM为矩形,
∵点A、B为反比例函数图象上的两点,A(m,n),N(0,2n),
∴S△BNO=S△AMO=k,S矩形ONCM=2mn=2k,
又∵S四边形OACB=4,
∴k+k+4=2mn=2k,
∴k=4.
故答案为:4.
【分析】由AM∥y轴,NB∥x轴,易得四边形ONCM为矩形,再根据反比例函数k的几何意义及图象上点的坐标特征可得S△BNO=S△AMO=k,S矩形ONCM=2mn=2k,又有S四边形OACB=4,从而可得到k+k+4=2mn=2k,解之即可求得k值.
12.【答案】①③④
【解析】【解答】解:①∵两个函数图象的交点为A,令y1=y2,
∴x=,
∴x=2,代入y1=x(x≥0),得:y=2,
∴A(2,2),故本选项正确;
②当x>2时,y1>2,y2<2,故本选项错误;
③当x=1时,y1=1,y2=4,
∴BC=y2﹣y1=4﹣1=3,故本选项正确;
④根据图象可知,y1随x的增大而增大,y2随x的增大而减小,故本选项正确.
所以①③④正确.
故答案为:①③④.
【分析】令y1=y2求出x、y的值,得到点A的坐标,据此判断①;根据图象以及点A的坐标可判断②;令x=1,求出y1、y2的值,进而判断③;根据图象可直接判断④.
13.【答案】(3,0)或(-3,0)或或
【解析】【解答】解:∵一次函数y= x+1与反比例函数y= 的图象交于点A、B,
∴的解是点A、B的坐标,
解这个方程组得:,,
∴A(-1,2),B(2,-1),
设P(n,0),
∵A(-1,2),B(2,-1),P(n,0),
∴AB2=(2+1)2+(1+2)2=18,BP2=(n-2)2+1,AP2=(n+1)2+4,
∵△ABP为直角三角形,
∴①当∠ABP=90°
AB2+BP2=AP2
∴18+(n-2)2+1=(n+1)2 +4,
∴n= 3,
∴ P(3, 0),
②当∠BAP= 90°时,
AB2+ AP2= BP2,
∴18+(n+1)2 +4=(n-2)2+1,
∴n= -3,
∴P(-3,0),
③当∠APB= 90°时,
AP2+ BP2= AB2,
∴(n+1)2+4+(n-2)2+1= 18,
∴
∴P(,0)或P(,0),
故答案为:P点的坐标(3,0)、 (-3,0)、(,0)或(,0).
【分析】根据一次函数y= x+1与反比例函数y= 的图象交于点A、B,得出点A、B的坐标,设P(n,0),根据A(-1,2),B(2,-1),P(n,0),得出△ABP为直角三角形,①当∠ABP=90°,②当∠BAP= 90°,③当∠APB= 90°,分类讨论即可。
14.【答案】
【解析】【解答】解:连接OC,BC,过点B作BD⊥x轴于点D,过点C作CE⊥x轴于点E,
∴∠BDO=∠OCE=90°,
∴∠BOD+∠OBD=90°,
∵AB=AC,∠BAC=60°,
∴△ABC是等边三角形,
∵ 直线y=k1x与双曲线y= 交于A、B两点,
∴OA=OB,
∴OC⊥AB,∠BCO=30°,
∴,
∴∠BOD+∠COE=90°,
∴∠OBD=∠COE,
∴△OBD∽△COE,
∴,
∵S△OBD=,S△OCE=,
∴,
∴.
故答案为:.
【分析】连接OC,BC,过点B作BD⊥x轴于点D,过点C作CE⊥x轴于点E,根据旋转的性质得出△ABC是等边三角形,根据反比例函数和一次函数的对称性得出OA=OB,得出OC⊥AB,∠BCO=30°,得出,再证出△OBD∽△COE,得出,利用反比例函数系数k的几何意义得出S△OBD=,S△OCE=,从而得出.
15.【答案】
【解析】【解答】解:过E作 于F,过D作 于G,
CD∥y轴,CE∥x轴,
直线 分别交x轴,y轴于点A和点B,点,
把 代入得:
同理:把 代入得:
,
同理:
故答案为; .
【分析】过E作 于F,过D作 于G, 由CD∥ y 轴,CE∥x轴,得 利用三角形相似的性质求解 建立方程求解,结合k的几何意义可得答案.
16.【答案】(1)解:将点A(-4,-3)代入
得m=12,
∴反比例函数解析式为:;
将A(-4,-3)与B(2,6)分别代入y=kx+b
得,解得
∴一次函数解析式为:;
(2)解:延长BC交x轴于点H,
四边形ABCD是矩形,
,
,
,
设直线BC的解析式为,
将点B(2,6)代入得,
解得,
∴直线BC的解析式为:
设,点C在直线BC上,∴,解得n=9,
,
设点D(x,y),
根据中点坐标公式得
,
解得,
;
(3)解:如图,过点E作EM⊥BP于点M,过点M作RQ⊥x轴,过点B作BR⊥RQ于点R,过点E作EQ⊥RQ于点Q,
为等边三角形,
,
,
,
设,,
,
点M为BP的中点,
,
,
∴.
【解析】【分析】(1)利用待定系数法即可分别求出两个函数的解析式;
(2)根据互相垂直的直线的比例系数的乘积等于-1可得直线BC的比例系数为,设直线BC的解析式为,将点B的坐标代入算出t的值,可得直线BC的解析式,设点,将其代入直线BC解析式可算出n的值,从而可得点C的坐标,设点D(x,y),根据中点坐标公式建立方程组,求解即可得出点D的坐标;
(3)如图,过点E作EM⊥BP于点M,过点M作RQ⊥x轴,过点B作BR⊥RQ于点R,过点E作EQ⊥RQ于点Q,根据等边三角形的性质得,设,,则,再由点M为BP的中点,可求解.
17.【答案】(1)解:每天生产口罩y(万个)与生产时间x(天)之间的函数表达式为:y= (x>4);
(2)解:由题意可得: ,
去分母整理得: ,
解得:x1=20,x2=﹣16,
经检验,x1=20,x2=﹣16是原分式方程的解,
但x=﹣16不合题意舍去,
∴20﹣4=16(天),
答:实际生产时间为16天.
【解析】【分析】(1)由生产总量=每天生产口罩 生产时间,即可求解;
(2)由题意列出方程,即可求解。
18.【答案】(1)解:当0≤x≤5时,
设一次函数解析式为y=kx+b,
把(0,15),(5,60)代入得 ,解得 ,
所以一次函数解析式为y=9x+15;
当x>5时,设反比例函数解析式为y= ,
把(5,60)代入得m=5×60=300,
所以反比例函数解析式为y=
(2)解:当y=15时, =15,解得x=20,
所以从开始加热到停止操作,共经历了20分钟。
【解析】【分析】(1)根据题意,可得知x≤5时,材料温度与加热时间是一次函数的关系;x>5时,温度与时间是反比例的关系,将点的坐标代入,可计算出解析式。
(2)将y值代入解析式,即可求得答案。
19.【答案】(1)解:由平均数,得x= ,即y= 是反比例函数;
(2)解:由单价乘以油量等于总价,得
y=4.75x,即y=4.75x是正比例函数;
(3)解:由路程与时间的关系,得
t= ,即t= 是反比例函数.
【解析】【分析】根据反比例函数的定义,可得答案.
20.【答案】(1)解:设
∵点(24,50)在其图象上,
∴所求函数关系式为
(2)解:由题意知,4台挖掘机每天能够开挖水渠30×4=120(米),当x=120时
答:该工程队需要用10天才能完成此项任务.
【解析】【分析】(1)利用图象可知点(24,50)在反比例函数图象上,设 ,将此点坐标代入函数解析式,可求出k的值,即可得到函数解析式.
(2)利用已知条件可得到4台挖掘机每天能够开挖水渠的长度,再将x=120代入函数解析式,可求出对应的y的值.
一、选择题
1.如图是反比例函数和(为常数)在第一象限内的图象,点M在的图象上,轴于点C,交的图象于点A,轴于点D,交的图象于点B,当点M在的图象上运动时,以下结论:①与的面积相等;②四边形的面积不变;③当点A是的中点时,则点B是的中点.其中错误结论的个数是( )
A.0 B.1 C.2 D.3
2.如图,已知点,,是轴上位于点上方的一点,平分,平分,直线交于点.若反比例函数的图像经过点,则的值是( )
A.-8 B.-9 C.-10 D.-12
3.如图,直线 与双曲线 交于 , ,直线AB交x轴于 ,下列命题:① ;②当 时, ;③若 为线段AB的中点,则 ,其中正确的命题有( )
A.①② B.②③ C.①③ D.①②③
4.如图,在平面直角坐标系中,一次函数 的图象与 轴、 轴分别相交于点 ,点 ,以线段 为边作正方形 ,且点 在反比例函数 的图象上,则 的值为( )
A. B. C. D.20
5.如图,正比例函数 的图象与反比例函数 的图象交于 , 两点, ,两边分别交 轴, 轴于点 , ,四边形 的面积为 , 轴于点 .有下列结论:① ;②三角形 的面积为 ;③线段 的长为 ;④不等式 的解集是 或 .其中正确结论的个数是( ).
A.1 B.2 C.3 D.4
6.如图在平面直角坐标系中,直线 分别与x轴、y轴交于点A、B,与 的图象交于点C、D.若CD = AB,则k的值为( )
A. . B. . C. . D. .
7.如图,平行于x轴的直线与函数y= (k1>0,x>0),y= (k2>0,x>0)的图象分别相交于A,B两点,点A在点B的右侧,C为x轴上的一个动点,若△ABC的面积为6,则k1﹣k2的值为( )
A.12 B.﹣12 C.6 D.﹣6
8.如图,矩形ABC0的两边OC,OA分别位于x轴,y轴上,点B的坐标为(- ,5),D是AB边上的一点,将△ADO沿直线OD翻折,使A点恰好落在对角线OB上的点E处,则过点E的反比例函数解析式是( )
A. B. C. D.
9.如图,一次函数y=-x+b与反比例函数y= (x>0)的图象交于A,B两点,与x轴、y轴分别交于C,D两点,连接OA,OB,过A作AE⊥x轴于点E,交OB于点F,设点A的横坐标为m.若S△OAF+S四边形EFBC=6,则m的值是( )
A.1 B. C. D.
10.如图,一次函数y=ax+b的图象与x轴、y轴交于A、B两点,与反比例函数 的图象相交于C、D两点,分别过C、D两点作y轴,x轴的垂线,垂足为E、F,连接CF、DE,有下列结论:①△CEF与△DEF的面积相等;②EF∥CD;③△DCE≌△CDF;④AC=BD;⑤△CEF的面积等于 ,其中正确的个数有( )
A.2 B.3 C.4 D.5
二、填空题
11.如图,在平面直角坐标系中,已知第一象限上的点A(m,n)是双曲线上的动点,过点A作AM∥y轴交x轴于点M,过点N(0,2n)作NB∥x轴交双曲线于点B,交直线AM于点C,若四边形OACB的面积为4,则k的值为 .
12.函数y1=x(x≥0),y2=(x>0)的图象如图所示,则以下4个结论:①两函数图象的交点A的坐标为(2,2);②当x>2时,y2>y1;③直线x=1与y1,y2依次交于C,B两点,则BC=3;④当x逐渐增大时,y1随着x的增大而增大y2随着x的增大而减小.其中正确结论的序号是 .
13.已知,一次函数与反比例函数的图象交于点A、B,在x轴上存在点P(n,0),使△ABP为直角三角形,则P点的坐标是 .
14.如图,已知直线y=k1x与双曲线y= 交于A B两点,将线段AB绕点A沿顺时针方向旋转60°后,点B落在点C处,双曲线y= 经过点C,则 的值是 。
15.如图,直线 分别交x轴,y轴于点A和点B,点C是反比例函数 的图象上位于直线下方的一点,CD∥y轴交AB于点D,CE∥x轴交AB于点E, ,则k的值为
三、综合题
16.反比例函数的图象与直线交点为、,点在点的左侧.
(1)如图1,求反比例函数和一次函数的解析式;
(2)如图2,点是反比例函数()上一点,点是平面内一点,连接,、,若四边形是矩形,求点的坐标;
(3)如图3,点是轴上一点,以为边向线段右侧作等边,若点在第四象限且到轴的距离是,求点的坐标.
17.新冠疫情期间,口罩的需求量增大,某口罩加工厂承揽生产1600万个口罩的任务,每天生产的口罩数量相同,计划用x天(x>4)完成.
(1)求每天生产口罩y(万个)与生产时间x(天)之间的函数表达式;
(2)由于疫情形势严峻,卫生管理部门要求厂家提前4天交货,那么加工厂每天要多做20万个口罩才能完成任务,求实际生产时间.
18.制作一种产品,需先将材料加热达到60℃后,再进行操作,设该材料温度为y(℃)从加热开始计算的时间为x(min).据了解,当该材料加热时,温度y与时间x成一次函数关系:停止加热进行操作时,温度y与时间x成反比例关系(如图).已知在操作加热前的温度为15℃,加热5分钟后温度达到60℃.
(1)分别求出将材料加热和停止加热进行操作时,y与x的函数关系式;
(2)根据工艺要求,当材料的温度低于15℃时,须停止操作,那么从开始加热到停止操作,共经历了多少时间?
19.列出下列问题中的函数关系式,并判断它们是否为反比例函数.
(1)某农场的粮食总产量为1 500t,则该农场人数y(人)与平均每人占有粮食量x(t)的函数关系式;
(2)在加油站,加油机显示器上显示的某一种油的单价为每升4.75元,总价从0元开始随着加油量的变化而变化,则总价y(元)与加油量x(L)的函数关系式;
(3)小明完成100m赛跑时,时间t(s)与他跑步的平均速度v(m/s)之间的函数关系式.
20.在工程实施过程中,某工程队接受一项开挖水渠的工程,所需天数y(天)与每天完成工程量x(米)是反比例函数关系,图象如图所示:
(1)求y与x之间的函数关系式
(2)若该工程队有4台挖掘机,每台挖掘机每天能够开挖水渠30米,问该工程队需要用多少天才能完成此项任务
1.【答案】A
【解析】【解答】∵点A、B在同一反比例函数的图像上,
∴.
故①符合题意;
∵点M在反比例函数的图象上,
∴.
∵,
∴.
故②符合题意;
连接,可知.
∵点A是的中点,
∴.
∵,
∴,
∴点B是的中点.
故③符合题意.
所以错误的个数是0.
故答案为:A.
【分析】利用反比例函数图象上的点坐标的特征和反比例函数k的几何意义逐项判断即可。
2.【答案】B
【解析】【解答】如图,过分别作的垂线,垂足分别为,,
平分,平分,
,
,
,
四边形是正方形
,,
故答案为:B
【分析】利用全等三角形的判定与性质,勾股定理,结合函数图象求解即可。
3.【答案】D
【解析】【解答】解:∵点A(x1,y1),B(x2,y2)在双曲线 上,
∴x1y1=x2y2=m2+1,
∴ ,①符合题意;
∵当x1<x<x2时,直线y=kx+b在双曲线 上方,
∴当 时, ,②符合题意;
∵M(t,s)为线段AB的中点,
∴ ,
当 时,
即 ,
此时, ,
∴ ,
把C(x0,0)代入y=kx+b得kx0+b=0,
解得 ,
∴x1+x2=x0,
∴ ,所以③符合题意.
故答案为:D.
【分析】根据反比例函数上的点横纵坐标之积相等,可得x1y1=x2y2,整理即可判断①;
结合函数图象一次函数在反比例函数上的的部分可对②进行判断;
根据线段的中点公式可得 ,联立反比例函数和一次函数整理后得一元二次方程 ,根据根与系数关系可得 ,由此可得 ,由一次函数与x轴的交点可得 ,由此可判断③.
4.【答案】A
【解析】【解答】解:∵一次函数 中,当x=0时,y=0+3=3,
∴A(0,3),
∴OA=3;
∵当y=0时,0= ,
∴x= 2,
∴B( 2,0),
∴OB=2;
过点C作CE⊥x轴于E,
∵四边形ABCD是正方形,
∴∠ABC=90°,AB=BC,
∵∠CBE+∠ABO=90°,∠BAO+∠ABO=90°,
∴∠CBE=∠BAO.
在△AOB和△BEC中, ,
∴△AOB≌△BEC(AAS),
∴BE=AO=3,CE=OB=2,
∴OE=2+3=5,
∴C点坐标为(-5,2),
∵点C在反比例函数 (x<0)图象上,
∴k= 5×2= 10.
故答案为:A.
【分析】过点C作CE⊥x轴于E,证明△AOB≌△BEC,可得点C坐标,代入求解即可.
5.【答案】B
【解析】【解答】解:∵正比例函数 的图象与反比例函数 的图象交于 , 两点
∴
∴
∴
结合题意,得 ,
∴ ,
∴ ,故①正确;
设点C坐标为 ,设点D坐标为 ,结合题意, 且
∴ ,
∵四边形 的面积为
∴四边形 的面积
∴
结合题意, ,
又∵ ,且
∴
∴
∴
∴
∴
∴ , , ,故③错误;
∵
∴ ,
∴
∴ ,故②正确;
当 时, 即
∴
∴ 或 (舍去)
当 时, 即
∴
∴
∴不等式 的解集是 或 ,故④错误;
故答案为:B.
【分析】根据正比例函数 的图象与反比例函数 的图象的性质,结合题意,可计算得 ;根据 和四边形 的面积为 ,设点C坐标为 ,设点D坐标为 ,通过勾股定理和四边形面积解方程,即可得到k的值,从而计算得 和三角形 的面积,以及不等式 的解集.
6.【答案】C
【解析】【解答】解:对直线y=﹣x+6,令x=0,则y=6,令y=0,则x=6,
∴点A、B的坐标分别为(6,0)、(0,6),
∴OB=OA=6,
∴AB=6 =3CD,∠BAO=45°,
∴ ,
联立y=﹣x+6和y= 并整理得:x2﹣6x+k=0,
设点C、D的横坐标分别为a,b,则a+b=6,ab=k,
∵∠BAO=45°,
∴CD= ,
∴CD2=2(a﹣b)2=2[(a+b)2﹣4ab]=2(36﹣4k)=(2 )2,解得:k=8.
故答案为:C.
【分析】先求出点A、B的坐标,于是可得AB的长,进而可得CD的长,设C、D的横坐标分别为a,b,则a,b是联立y=﹣x+6和y= 并整理后的方程的解,由CD= 并结合根与系数的关系可得关于k的方程,解方程即可求出k,从而可得答案.
7.【答案】A
【解析】【解答】解:设:A、B点的坐标分别是A( ,m)、B( ,m),
则:△ABC的面积= AB yA= ( ﹣ ) m=6,
则k1﹣k2=12.
故答案为:A.
【分析】△ABC的面积= AB yA,先设A、B两点坐标(其y坐标相同),然后计算相应线段长度,用面积公式即可求解.
8.【答案】C
【解析】【解答】解:过E作EF⊥OC交OC于点F,如图:
∵矩形ABCO中,
∴BC⊥OC,
∵EF⊥OC,
∴EF∥BC,
∴△OEF∽△OBC,
∴,
∵B(-,5),
∴BC=5,OC=-,
即=,
∴令EF=3x,OF=4x,
根据翻折的性质可知OA=OE=BC=5,
在Rt△OEF中,
∴(3x)2+(4x)2=52,
解得:x=1,
∴EF=3,OF=4,
∴E(-4,3),
设经过点E的反比例函数解析式为:y=,
又∵点E(-4,3)在反比例函数上,
∴k=-4×3=-12,
∴经过点E的反比例函数解析式为:y=.
故答案为:C.
【分析】解:过E作EF⊥OC交OC于点F,如图:
∵矩形ABCO中,
∴BC⊥OC,
∵EF⊥OC,
∴EF∥BC,
∴△OEF∽△OBC,
∴,
∵B(-,5),
∴BC=5,OC=-,
即=,
∴令EF=3x,OF=4x,
根据翻折的性质可知OA=OE=BC=5,
在Rt△OEF中,
∴(3x)2+(4x)2=52,
解得:x=1,
∴EF=3,OF=4,
∴E(-4,3),
设经过点E的反比例函数解析式为:y=,
又∵点E(-4,3)在反比例函数上,
∴k=-4×3=-12,
∴经过点E的反比例函数解析式为:y=.
故答案为:C.
【分析】过E作EF⊥OC交OC于点F,根据矩形的性质和相似三角形的判定得△OEF∽△OBC,由相似三角形的性质得=,从而令EF=3x,OF=4x,几何翻折的性质可知OE=5,在Rt△OEF中,根据勾股定理列出方程,解之得出x值,从而可得E点坐标,根据待定系数法即可求得经过点E的反比例函数解析式.
9.【答案】C
【解析】【解答】解:∵A点在反比例函数y=(x>0),且A点横坐标为m,
∴A(m,),
又∵A点在一次函数y=-x+b上,
∴A(m,-m+b),
∴=-m+b,
即b=m+,
作AM⊥OD于M,BN⊥OC于N,如图:
∵反比例函数y=与一次函数y=-x+b均关于直线y=x对称,
∴AD=BC,OD=OC,DM=AM=BN=CN,
设S△AOF=s,
则S△OEF=3-s,S四边形EFBC=6-s,S△OBC=S△OAD=9-2s,S△ADM=6-2s=2(3-s),
∴S△ADM=2S△OEF,
由对称性可知:AD=BC,OD,∠ODC=∠OCD=45°,
∴△AOM≌△BON,
∵AM=BN=DM=CN,
∴EF=AM=BN,
∴EF是△BON的中位线,
∴N(2m,0),
∴B(2m,),
又∵点B在一次函数y=-x+b上,
∴=-2m+m+,
整理得:m2=3,
∵m>0,
∴m=.
故答案为:C.
【分析】由A是反比例函数与一次函数的交点得 =-m+b,即b=m+,作AM⊥OD于M,BN⊥OC于N,设S△AOF=s,则S△OEF=2-s,S四边形EFBC=4-s,S△OBC=S△OAD=6-2s,S△ADM=4-2s=2(2-s), 从而得S△ADM=2S△OEF,根据对称性和全等三角形的性质可得 EF是△BON的中位线,由此得B(2m,),将点B坐标代入一次函数解析式即可求得m值.
10.【答案】C
【解析】【解答】解:设点D的坐标为(x,kx),则F(x,0).
由函数的图象可知:x>0,k>0. ∴S△DFE= DF OF= |xD| | |= k,
同理可得S△CEF= k,故⑤正确; 故S△DEF=S△CEF.故①正确;
若两个三角形以EF为底,则EF边上的高相等,故CD∥EF.故②正确;
③条件不足,无法得到判定两三角形全等的条件,故③错误;
④法一:∵CD∥EF,DF∥BE,
∴四边形DBEF是平行四边形,
∴S△DEF=S△BED, 同理可得S△ACF=S△ECF;
由①得:S△DBE=S△ACF. 又∵CD∥EF,BD、AC边上的高相等,
∴BD=AC,故④正确;
法2:∵四边形ACEF,四边形BDEF都是平行四边形, 而且EF是公共边, 即AC=EF=BD,
∴BD=AC,故④正确; 因此正确的结论有4个:①②④⑤.
故答案为:C.
【分析】此题要根据反比例函数的性质进行求解,解决此题的关键是要证出CD∥EF,可从①问的面积相等入手;△DFE中,以DF为底,OF为高,可得S△DFE=|xD| |yD|=k,同理可求得△CEF的面积也是k,因此两者的面积相等;若两个三角形都以EF为底,那么它们的高相同,即E、F到AD的距离相等,由此可证得CD∥EF,然后根据这个条件来逐一判断各选项的正误.
11.【答案】4
【解析】【解答】解:∵AM∥y轴,NB∥x轴,
∴四边形ONCM为矩形,
∵点A、B为反比例函数图象上的两点,A(m,n),N(0,2n),
∴S△BNO=S△AMO=k,S矩形ONCM=2mn=2k,
又∵S四边形OACB=4,
∴k+k+4=2mn=2k,
∴k=4.
故答案为:4.
【分析】由AM∥y轴,NB∥x轴,易得四边形ONCM为矩形,再根据反比例函数k的几何意义及图象上点的坐标特征可得S△BNO=S△AMO=k,S矩形ONCM=2mn=2k,又有S四边形OACB=4,从而可得到k+k+4=2mn=2k,解之即可求得k值.
12.【答案】①③④
【解析】【解答】解:①∵两个函数图象的交点为A,令y1=y2,
∴x=,
∴x=2,代入y1=x(x≥0),得:y=2,
∴A(2,2),故本选项正确;
②当x>2时,y1>2,y2<2,故本选项错误;
③当x=1时,y1=1,y2=4,
∴BC=y2﹣y1=4﹣1=3,故本选项正确;
④根据图象可知,y1随x的增大而增大,y2随x的增大而减小,故本选项正确.
所以①③④正确.
故答案为:①③④.
【分析】令y1=y2求出x、y的值,得到点A的坐标,据此判断①;根据图象以及点A的坐标可判断②;令x=1,求出y1、y2的值,进而判断③;根据图象可直接判断④.
13.【答案】(3,0)或(-3,0)或或
【解析】【解答】解:∵一次函数y= x+1与反比例函数y= 的图象交于点A、B,
∴的解是点A、B的坐标,
解这个方程组得:,,
∴A(-1,2),B(2,-1),
设P(n,0),
∵A(-1,2),B(2,-1),P(n,0),
∴AB2=(2+1)2+(1+2)2=18,BP2=(n-2)2+1,AP2=(n+1)2+4,
∵△ABP为直角三角形,
∴①当∠ABP=90°
AB2+BP2=AP2
∴18+(n-2)2+1=(n+1)2 +4,
∴n= 3,
∴ P(3, 0),
②当∠BAP= 90°时,
AB2+ AP2= BP2,
∴18+(n+1)2 +4=(n-2)2+1,
∴n= -3,
∴P(-3,0),
③当∠APB= 90°时,
AP2+ BP2= AB2,
∴(n+1)2+4+(n-2)2+1= 18,
∴
∴P(,0)或P(,0),
故答案为:P点的坐标(3,0)、 (-3,0)、(,0)或(,0).
【分析】根据一次函数y= x+1与反比例函数y= 的图象交于点A、B,得出点A、B的坐标,设P(n,0),根据A(-1,2),B(2,-1),P(n,0),得出△ABP为直角三角形,①当∠ABP=90°,②当∠BAP= 90°,③当∠APB= 90°,分类讨论即可。
14.【答案】
【解析】【解答】解:连接OC,BC,过点B作BD⊥x轴于点D,过点C作CE⊥x轴于点E,
∴∠BDO=∠OCE=90°,
∴∠BOD+∠OBD=90°,
∵AB=AC,∠BAC=60°,
∴△ABC是等边三角形,
∵ 直线y=k1x与双曲线y= 交于A、B两点,
∴OA=OB,
∴OC⊥AB,∠BCO=30°,
∴,
∴∠BOD+∠COE=90°,
∴∠OBD=∠COE,
∴△OBD∽△COE,
∴,
∵S△OBD=,S△OCE=,
∴,
∴.
故答案为:.
【分析】连接OC,BC,过点B作BD⊥x轴于点D,过点C作CE⊥x轴于点E,根据旋转的性质得出△ABC是等边三角形,根据反比例函数和一次函数的对称性得出OA=OB,得出OC⊥AB,∠BCO=30°,得出,再证出△OBD∽△COE,得出,利用反比例函数系数k的几何意义得出S△OBD=,S△OCE=,从而得出.
15.【答案】
【解析】【解答】解:过E作 于F,过D作 于G,
CD∥y轴,CE∥x轴,
直线 分别交x轴,y轴于点A和点B,点,
把 代入得:
同理:把 代入得:
,
同理:
故答案为; .
【分析】过E作 于F,过D作 于G, 由CD∥ y 轴,CE∥x轴,得 利用三角形相似的性质求解 建立方程求解,结合k的几何意义可得答案.
16.【答案】(1)解:将点A(-4,-3)代入
得m=12,
∴反比例函数解析式为:;
将A(-4,-3)与B(2,6)分别代入y=kx+b
得,解得
∴一次函数解析式为:;
(2)解:延长BC交x轴于点H,
四边形ABCD是矩形,
,
,
,
设直线BC的解析式为,
将点B(2,6)代入得,
解得,
∴直线BC的解析式为:
设,点C在直线BC上,∴,解得n=9,
,
设点D(x,y),
根据中点坐标公式得
,
解得,
;
(3)解:如图,过点E作EM⊥BP于点M,过点M作RQ⊥x轴,过点B作BR⊥RQ于点R,过点E作EQ⊥RQ于点Q,
为等边三角形,
,
,
,
设,,
,
点M为BP的中点,
,
,
∴.
【解析】【分析】(1)利用待定系数法即可分别求出两个函数的解析式;
(2)根据互相垂直的直线的比例系数的乘积等于-1可得直线BC的比例系数为,设直线BC的解析式为,将点B的坐标代入算出t的值,可得直线BC的解析式,设点,将其代入直线BC解析式可算出n的值,从而可得点C的坐标,设点D(x,y),根据中点坐标公式建立方程组,求解即可得出点D的坐标;
(3)如图,过点E作EM⊥BP于点M,过点M作RQ⊥x轴,过点B作BR⊥RQ于点R,过点E作EQ⊥RQ于点Q,根据等边三角形的性质得,设,,则,再由点M为BP的中点,可求解.
17.【答案】(1)解:每天生产口罩y(万个)与生产时间x(天)之间的函数表达式为:y= (x>4);
(2)解:由题意可得: ,
去分母整理得: ,
解得:x1=20,x2=﹣16,
经检验,x1=20,x2=﹣16是原分式方程的解,
但x=﹣16不合题意舍去,
∴20﹣4=16(天),
答:实际生产时间为16天.
【解析】【分析】(1)由生产总量=每天生产口罩 生产时间,即可求解;
(2)由题意列出方程,即可求解。
18.【答案】(1)解:当0≤x≤5时,
设一次函数解析式为y=kx+b,
把(0,15),(5,60)代入得 ,解得 ,
所以一次函数解析式为y=9x+15;
当x>5时,设反比例函数解析式为y= ,
把(5,60)代入得m=5×60=300,
所以反比例函数解析式为y=
(2)解:当y=15时, =15,解得x=20,
所以从开始加热到停止操作,共经历了20分钟。
【解析】【分析】(1)根据题意,可得知x≤5时,材料温度与加热时间是一次函数的关系;x>5时,温度与时间是反比例的关系,将点的坐标代入,可计算出解析式。
(2)将y值代入解析式,即可求得答案。
19.【答案】(1)解:由平均数,得x= ,即y= 是反比例函数;
(2)解:由单价乘以油量等于总价,得
y=4.75x,即y=4.75x是正比例函数;
(3)解:由路程与时间的关系,得
t= ,即t= 是反比例函数.
【解析】【分析】根据反比例函数的定义,可得答案.
20.【答案】(1)解:设
∵点(24,50)在其图象上,
∴所求函数关系式为
(2)解:由题意知,4台挖掘机每天能够开挖水渠30×4=120(米),当x=120时
答:该工程队需要用10天才能完成此项任务.
【解析】【分析】(1)利用图象可知点(24,50)在反比例函数图象上,设 ,将此点坐标代入函数解析式,可求出k的值,即可得到函数解析式.
(2)利用已知条件可得到4台挖掘机每天能够开挖水渠的长度,再将x=120代入函数解析式,可求出对应的y的值.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
