鲁教版七年级数学上册期末总复习第1章 三角形复习测试题(含答案)
文档属性
| 名称 | 鲁教版七年级数学上册期末总复习第1章 三角形复习测试题(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 305.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-01-09 14:06:24 | ||
图片预览


文档简介
鲁教版七年级数学上册期末总复习第1单元三角形复习测试题(含答案)
一.选择题(共15小题)
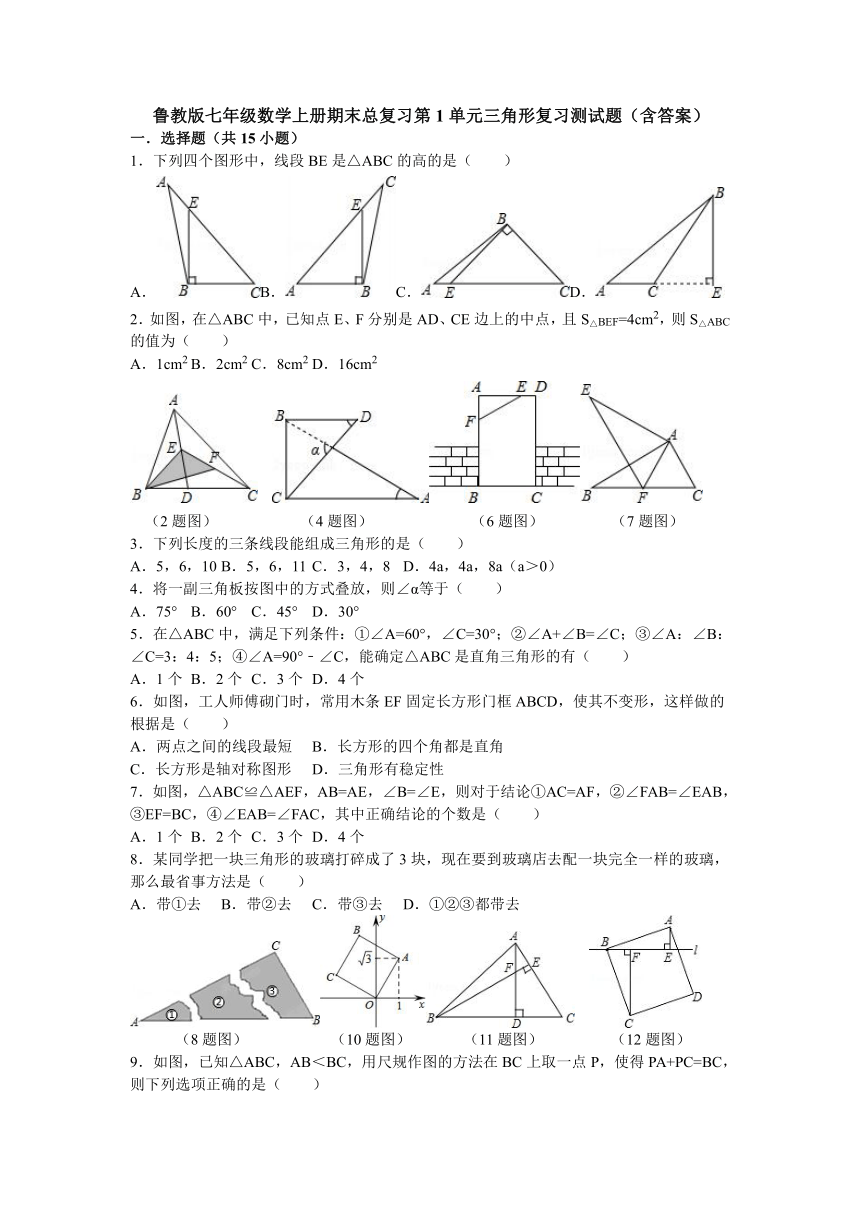
1.下列四个图形中,线段BE是△ABC的高的是( )
A.B.C.D.
2.如图,在△ABC中,已知点E、F分别是AD、CE边上的中点,且S△BEF=4cm2,则S△ABC的值为( )
A.1cm2 B.2cm2 C.8cm2 D.16cm2
(2题图) (4题图) (6题图) (7题图)
3.下列长度的三条线段能组成三角形的是( )
A.5,6,10 B.5,6,11 C.3,4,8 D.4a,4a,8a(a>0)
4.将一副三角板按图中的方式叠放,则∠α等于( )
A.75° B.60° C.45° D.30°
5.在△ABC中,满足下列条件:①∠A=60°,∠C=30°;②∠A+∠B=∠C;③∠A:∠B:∠C=3:4:5;④∠A=90°﹣∠C,能确定△ABC是直角三角形的有( )
A.1个 B.2个 C.3个 D.4个
6.如图,工人师傅砌门时,常用木条EF固定长方形门框ABCD,使其不变形,这样做的根据是( )
A.两点之间的线段最短 B.长方形的四个角都是直角
C.长方形是轴对称图形 D.三角形有稳定性
7.如图,△ABC≌△AEF,AB=AE,∠B=∠E,则对于结论①AC=AF,②∠FAB=∠EAB,③EF=BC,④∠EAB=∠FAC,其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
8.某同学把一块三角形的玻璃打碎成了3块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事方法是( )
A.带①去 B.带②去 C.带③去 D.①②③都带去
(8题图) (10题图) (11题图) (12题图)
9.如图,已知△ABC,AB<BC,用尺规作图的方法在BC上取一点P,使得PA+PC=BC,则下列选项正确的是( )
A.B. C. D.
10.如图,将正方形OABC放在平面直角坐标系中,O是原点,A的坐标为(1,),则点C的坐标为( )
A.(﹣1,) B.(﹣,1) C.(﹣2,1) D.(﹣1,2)
11.如图,在△ABC中,∠ABC=45°,AC=5,F是高AD和BE的交点,则BF的长是( )
A.7 B.6 C.5 D.4
12.如图,过正方形ABCD的顶点B作直线l,过A、C作直线L的垂线,垂足分别为E、F,若AE=1,CF=2,则AB的长为( )
A. B.2 C.3 D.
13.如图,直线l上有三个正方形A、B、C,若正方形A、C的面积分别为5和11,则正方形B的面积为( )
A.4 B.6 C.16 D.55
(13题图) (14题图) (15题图)
14.如图,在△ABC中,∠ACB=90°,AC=BC,点F在AB上,连接CF,AE⊥CF于E,BD垂直CF的延长线于点D.若AE=4cm,BD=2cm,则EF的长是( )
A.cm B.cm C.1cm D.cm
15.已知,如图,△ABC中,AB=AC,AD是角平分线,BE=CF,则下列说法正确的有几个(1)DA平分∠EDF;(2)△EBD≌△FCD;(3)△AED≌△AFD;(4)AD垂直BC.( )A.1个 B.2个 C.3个 D.4个
二.填空题(共7小题)
16.已知三角形的两边分别是5和10,则第三边长x的取值范围是 .
17.已知△ABC底边BC上的高为8cm,当它的底边BC从16cm变化到5cm时,△ABC的面积减少了 cm2.
18.如图,若CD平分∠ACE,BD平分∠ABC,∠A=45°,则∠D= °.
(18题图) (19题图) (20题图) (21题图)
19.如图所示,在折纸活动中,小明制作了一张△ABC纸片,点D,E分别在边AB、AC
上,将△ABC沿着DE折叠压平,使点A与点N重合.
(1)若∠B=35°,∠C=60°,则∠A的度数为 ;
(2)若∠A=70°,则∠1+∠2的度数为 .
20.如图是由4个相同的小正方形组成的网格图,其中∠1+∠2等于 .
21.如图,△ABC≌△ADE,BC的延长线交DA于F,交DE于G,∠D=25°,∠E=105°,
∠DAC=16°,则∠DGB= .
22.如图,点B,F,C,E在同一直线上,BF=CE,AB∥DE,请添加一个条件,使△ABC≌△DEF,这个添加的条件可以是 (只需写一个,不添加辅助线).
(22题图) (23题图)
三.解答题(共8小题)
23.(1)如图①,你知道∠BOC=∠B+∠C+∠A的奥秘吗?请用你学过的知识予以证明;
(2)如图②,设x=∠A+∠B+∠C+∠D+∠E,运用(1)中的结论填空.
x= °; x= °; x= °;
(3)如图③,一个六角星,其中∠BOD=70°,则:∠A+∠B+∠C+∠D+∠E+∠F= °.
24.如图,∠BAC=∠CDB=90°,请你从下列条件中任选一个,使得△BAC≌△CDA,并证明.①AB=CD;②AC=DB;③∠ABC=∠DCB;④∠ACB=∠DBC.
25.如图,在直角三角形ABC中,∠ABC=90°,点D在BC的延长线上,且BD=AB,过B作BE⊥AC,与BD的垂线DE交于点E.求证:△ABC≌△BDE.
26.如图,点C,E,F,B在同一直线上,点A,D在BC异侧,AB∥CD,AE=DF,∠A=∠D.
(1)求证:AB=CD.
(2)若AB=CF,∠B=30°,求∠D的度数.
27.用圆规、直尺作图,不写作法,但要保留作图痕迹.
已知:线段c,直线l及l外一点A.
求作:Rt△ABC,使直角边为AC(AC⊥l,垂足为C),斜边AB=c.
28.如图,幼儿园的滑梯有两个长度相等滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等.
(1)△ABC与△DEF全等吗?
(2)两个滑梯的倾斜角∠ABC与∠DFE的大小有什么关系.
29.要测量河两岸相对两点A,B间的距离,先在过点B的AB的垂线上取两点C、D,使CD=BC,再在过点D的l的垂线上取点E,使A、C、E三点在一条直线上,这时ED的长就是A,B两点间的距离.你知道为什么吗?说说你的理由.
30.如图,河岸上A、B两点相距25km,C、D为两村庄,DA⊥AB于点A,CB⊥AB与点B,已知DA=10km,CB=15km,现在AB上建一个水泵站E,使得C,D两村到E站的距离相等.求E应建在距A多远处?
鲁教版七年级数学上册期末总复习第1单元复习测试题
参考答案
一.选择题(共15小题)
1.D; 2.D; 3.A; 4.A; 5.C; 6.D; 7.C; 8.C; 9.D; 10.B;11.C; 12.D; 13.C; 14.D; 15.D;
二.填空题(共7小题)
16.5<x<15; 17.44; 18.22.5; 19.85°; 140°; 20.180°;
21.66°; 22.AB=DE;
三.解答题(共8小题)
23.解:(1)如图①,延长BO交AC于点D,
∠BOC=∠BDC+∠C,
又∵∠BDC=∠A+∠B,
∴∠BOC=∠B+∠C+∠A.
(2)如图②,
根据外角的性质,可得
∠1=∠A+∠B,∠2=∠C+∠D,
∵∠1+∠2+∠E=180°,
∴x=∠A+∠B+∠C+∠D+∠E=180°.
如图③,根据外角的性质,可得
∠1=∠A+∠B,∠2=∠C+∠D,
∵∠1+∠2+∠E=180°,
∴x=∠A+∠B+∠C+∠D+∠E=180°.
如图④,延长EA交CD于点F,EA和BC交于点G,根据外角的性质,可得
∠GFC=∠D+∠E,∠FGC=∠A+∠B,
∵∠GFC+∠FGC+∠C=180°,
∴x=∠A+∠B+∠C+∠D+∠E=180°.
(3)如图⑤,
∵∠BOD=70°,
∴∠A+∠C+∠E=70°,
∴∠B+∠D+∠F=70°,
∴∠A+∠B+∠C+∠D+∠E+∠F=70°+70°=140°.
故答案为:180、180、180、140.
24.解:选①AB=CD.理由如下:
∵∠BAC=∠CDB=90°,∴△BAC和△CDA是直角三角形,
在Rt△△BAC和Rt△CDA中,,∴Rt△BAC≌Rt△CDA(HL).
25.证明:在Rt△ABC中,
∵∠ABC=90°,∴∠ABE+∠DBE=90°,
∵BE⊥AC,∴∠ABE+∠A=90°,∴∠A=∠DBE,
∵DE是BD的垂线,∴∠D=90°,
在△ABC和△BDE中,∵,∴△ABC≌△BDE(ASA).
26.证明:(1)∵AB∥CD,∴∠B=∠C,
在△ABE和△CDF中,,∴△ABE≌△CDF(AAS),∴AB=CD;
(2)∵△ABE≌△CDF,∴AB=CD,BE=CF,
∵AB=CF,∠B=30°,∴AB=BE,∴△ABE是等腰三角形,
∴∠D=.
27.解:如图,△ABC为所求.
28.解:(1)△ABC与△DEF全等.理由如下:
在Rt△ABC与Rt△DEF中,,∴Rt△ABC≌Rt△DEF(HL);
(2)∠ABC+∠DFE=90°,理由如下:
由(1)知,Rt△ABC≌Rt△DEF,则∠ABC=∠DEF,
∵∠DEF+∠DFE=90°,
∴∠ABC+∠DFE=90°.
29.解:∵AB⊥l,CD⊥l,
∴∠ABC=∠EDC=90°,
在△ABC和△EDC中,,∴△ABC≌△EDC(ASA),∴AB=DE,
即ED的长就是A,B两点间的距离.
30.解:设AE=xkm,
∵C、D两村到E站的距离相等,
∴DE=CE,即DE2=CE2,
由勾股定理,得102+x2=152+(25﹣x)2,
解得:x=15.
故:E点应建在距A站15千米处.
一.选择题(共15小题)
1.下列四个图形中,线段BE是△ABC的高的是( )
A.B.C.D.
2.如图,在△ABC中,已知点E、F分别是AD、CE边上的中点,且S△BEF=4cm2,则S△ABC的值为( )
A.1cm2 B.2cm2 C.8cm2 D.16cm2
(2题图) (4题图) (6题图) (7题图)
3.下列长度的三条线段能组成三角形的是( )
A.5,6,10 B.5,6,11 C.3,4,8 D.4a,4a,8a(a>0)
4.将一副三角板按图中的方式叠放,则∠α等于( )
A.75° B.60° C.45° D.30°
5.在△ABC中,满足下列条件:①∠A=60°,∠C=30°;②∠A+∠B=∠C;③∠A:∠B:∠C=3:4:5;④∠A=90°﹣∠C,能确定△ABC是直角三角形的有( )
A.1个 B.2个 C.3个 D.4个
6.如图,工人师傅砌门时,常用木条EF固定长方形门框ABCD,使其不变形,这样做的根据是( )
A.两点之间的线段最短 B.长方形的四个角都是直角
C.长方形是轴对称图形 D.三角形有稳定性
7.如图,△ABC≌△AEF,AB=AE,∠B=∠E,则对于结论①AC=AF,②∠FAB=∠EAB,③EF=BC,④∠EAB=∠FAC,其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
8.某同学把一块三角形的玻璃打碎成了3块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事方法是( )
A.带①去 B.带②去 C.带③去 D.①②③都带去
(8题图) (10题图) (11题图) (12题图)
9.如图,已知△ABC,AB<BC,用尺规作图的方法在BC上取一点P,使得PA+PC=BC,则下列选项正确的是( )
A.B. C. D.
10.如图,将正方形OABC放在平面直角坐标系中,O是原点,A的坐标为(1,),则点C的坐标为( )
A.(﹣1,) B.(﹣,1) C.(﹣2,1) D.(﹣1,2)
11.如图,在△ABC中,∠ABC=45°,AC=5,F是高AD和BE的交点,则BF的长是( )
A.7 B.6 C.5 D.4
12.如图,过正方形ABCD的顶点B作直线l,过A、C作直线L的垂线,垂足分别为E、F,若AE=1,CF=2,则AB的长为( )
A. B.2 C.3 D.
13.如图,直线l上有三个正方形A、B、C,若正方形A、C的面积分别为5和11,则正方形B的面积为( )
A.4 B.6 C.16 D.55
(13题图) (14题图) (15题图)
14.如图,在△ABC中,∠ACB=90°,AC=BC,点F在AB上,连接CF,AE⊥CF于E,BD垂直CF的延长线于点D.若AE=4cm,BD=2cm,则EF的长是( )
A.cm B.cm C.1cm D.cm
15.已知,如图,△ABC中,AB=AC,AD是角平分线,BE=CF,则下列说法正确的有几个(1)DA平分∠EDF;(2)△EBD≌△FCD;(3)△AED≌△AFD;(4)AD垂直BC.( )A.1个 B.2个 C.3个 D.4个
二.填空题(共7小题)
16.已知三角形的两边分别是5和10,则第三边长x的取值范围是 .
17.已知△ABC底边BC上的高为8cm,当它的底边BC从16cm变化到5cm时,△ABC的面积减少了 cm2.
18.如图,若CD平分∠ACE,BD平分∠ABC,∠A=45°,则∠D= °.
(18题图) (19题图) (20题图) (21题图)
19.如图所示,在折纸活动中,小明制作了一张△ABC纸片,点D,E分别在边AB、AC
上,将△ABC沿着DE折叠压平,使点A与点N重合.
(1)若∠B=35°,∠C=60°,则∠A的度数为 ;
(2)若∠A=70°,则∠1+∠2的度数为 .
20.如图是由4个相同的小正方形组成的网格图,其中∠1+∠2等于 .
21.如图,△ABC≌△ADE,BC的延长线交DA于F,交DE于G,∠D=25°,∠E=105°,
∠DAC=16°,则∠DGB= .
22.如图,点B,F,C,E在同一直线上,BF=CE,AB∥DE,请添加一个条件,使△ABC≌△DEF,这个添加的条件可以是 (只需写一个,不添加辅助线).
(22题图) (23题图)
三.解答题(共8小题)
23.(1)如图①,你知道∠BOC=∠B+∠C+∠A的奥秘吗?请用你学过的知识予以证明;
(2)如图②,设x=∠A+∠B+∠C+∠D+∠E,运用(1)中的结论填空.
x= °; x= °; x= °;
(3)如图③,一个六角星,其中∠BOD=70°,则:∠A+∠B+∠C+∠D+∠E+∠F= °.
24.如图,∠BAC=∠CDB=90°,请你从下列条件中任选一个,使得△BAC≌△CDA,并证明.①AB=CD;②AC=DB;③∠ABC=∠DCB;④∠ACB=∠DBC.
25.如图,在直角三角形ABC中,∠ABC=90°,点D在BC的延长线上,且BD=AB,过B作BE⊥AC,与BD的垂线DE交于点E.求证:△ABC≌△BDE.
26.如图,点C,E,F,B在同一直线上,点A,D在BC异侧,AB∥CD,AE=DF,∠A=∠D.
(1)求证:AB=CD.
(2)若AB=CF,∠B=30°,求∠D的度数.
27.用圆规、直尺作图,不写作法,但要保留作图痕迹.
已知:线段c,直线l及l外一点A.
求作:Rt△ABC,使直角边为AC(AC⊥l,垂足为C),斜边AB=c.
28.如图,幼儿园的滑梯有两个长度相等滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等.
(1)△ABC与△DEF全等吗?
(2)两个滑梯的倾斜角∠ABC与∠DFE的大小有什么关系.
29.要测量河两岸相对两点A,B间的距离,先在过点B的AB的垂线上取两点C、D,使CD=BC,再在过点D的l的垂线上取点E,使A、C、E三点在一条直线上,这时ED的长就是A,B两点间的距离.你知道为什么吗?说说你的理由.
30.如图,河岸上A、B两点相距25km,C、D为两村庄,DA⊥AB于点A,CB⊥AB与点B,已知DA=10km,CB=15km,现在AB上建一个水泵站E,使得C,D两村到E站的距离相等.求E应建在距A多远处?
鲁教版七年级数学上册期末总复习第1单元复习测试题
参考答案
一.选择题(共15小题)
1.D; 2.D; 3.A; 4.A; 5.C; 6.D; 7.C; 8.C; 9.D; 10.B;11.C; 12.D; 13.C; 14.D; 15.D;
二.填空题(共7小题)
16.5<x<15; 17.44; 18.22.5; 19.85°; 140°; 20.180°;
21.66°; 22.AB=DE;
三.解答题(共8小题)
23.解:(1)如图①,延长BO交AC于点D,
∠BOC=∠BDC+∠C,
又∵∠BDC=∠A+∠B,
∴∠BOC=∠B+∠C+∠A.
(2)如图②,
根据外角的性质,可得
∠1=∠A+∠B,∠2=∠C+∠D,
∵∠1+∠2+∠E=180°,
∴x=∠A+∠B+∠C+∠D+∠E=180°.
如图③,根据外角的性质,可得
∠1=∠A+∠B,∠2=∠C+∠D,
∵∠1+∠2+∠E=180°,
∴x=∠A+∠B+∠C+∠D+∠E=180°.
如图④,延长EA交CD于点F,EA和BC交于点G,根据外角的性质,可得
∠GFC=∠D+∠E,∠FGC=∠A+∠B,
∵∠GFC+∠FGC+∠C=180°,
∴x=∠A+∠B+∠C+∠D+∠E=180°.
(3)如图⑤,
∵∠BOD=70°,
∴∠A+∠C+∠E=70°,
∴∠B+∠D+∠F=70°,
∴∠A+∠B+∠C+∠D+∠E+∠F=70°+70°=140°.
故答案为:180、180、180、140.
24.解:选①AB=CD.理由如下:
∵∠BAC=∠CDB=90°,∴△BAC和△CDA是直角三角形,
在Rt△△BAC和Rt△CDA中,,∴Rt△BAC≌Rt△CDA(HL).
25.证明:在Rt△ABC中,
∵∠ABC=90°,∴∠ABE+∠DBE=90°,
∵BE⊥AC,∴∠ABE+∠A=90°,∴∠A=∠DBE,
∵DE是BD的垂线,∴∠D=90°,
在△ABC和△BDE中,∵,∴△ABC≌△BDE(ASA).
26.证明:(1)∵AB∥CD,∴∠B=∠C,
在△ABE和△CDF中,,∴△ABE≌△CDF(AAS),∴AB=CD;
(2)∵△ABE≌△CDF,∴AB=CD,BE=CF,
∵AB=CF,∠B=30°,∴AB=BE,∴△ABE是等腰三角形,
∴∠D=.
27.解:如图,△ABC为所求.
28.解:(1)△ABC与△DEF全等.理由如下:
在Rt△ABC与Rt△DEF中,,∴Rt△ABC≌Rt△DEF(HL);
(2)∠ABC+∠DFE=90°,理由如下:
由(1)知,Rt△ABC≌Rt△DEF,则∠ABC=∠DEF,
∵∠DEF+∠DFE=90°,
∴∠ABC+∠DFE=90°.
29.解:∵AB⊥l,CD⊥l,
∴∠ABC=∠EDC=90°,
在△ABC和△EDC中,,∴△ABC≌△EDC(ASA),∴AB=DE,
即ED的长就是A,B两点间的距离.
30.解:设AE=xkm,
∵C、D两村到E站的距离相等,
∴DE=CE,即DE2=CE2,
由勾股定理,得102+x2=152+(25﹣x)2,
解得:x=15.
故:E点应建在距A站15千米处.
