鲁教版七年级数学上册期末总复习第2章 轴对称复习测试题(含答案)
文档属性
| 名称 | 鲁教版七年级数学上册期末总复习第2章 轴对称复习测试题(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 288.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-01-09 14:06:39 | ||
图片预览



文档简介
鲁教版七年级数学上册期末总复习第2单元轴对称测试题(含答案)
一.选择题(共13小题)
1.下面四个图形分别是节能、节水、低碳和绿色食品标志,在这四个标志中,是轴对称图形的是( )
A. B. C. D.
2.电子钟镜子里的像如图所示,实际时间是( )
A.21:10 B.10:21 C.10:51 D.12:01
(2题图) (4题图) (5题图) (6题图) (7题图)
3.下列图形中对称轴只有两条的是( )
A.B. C. D.
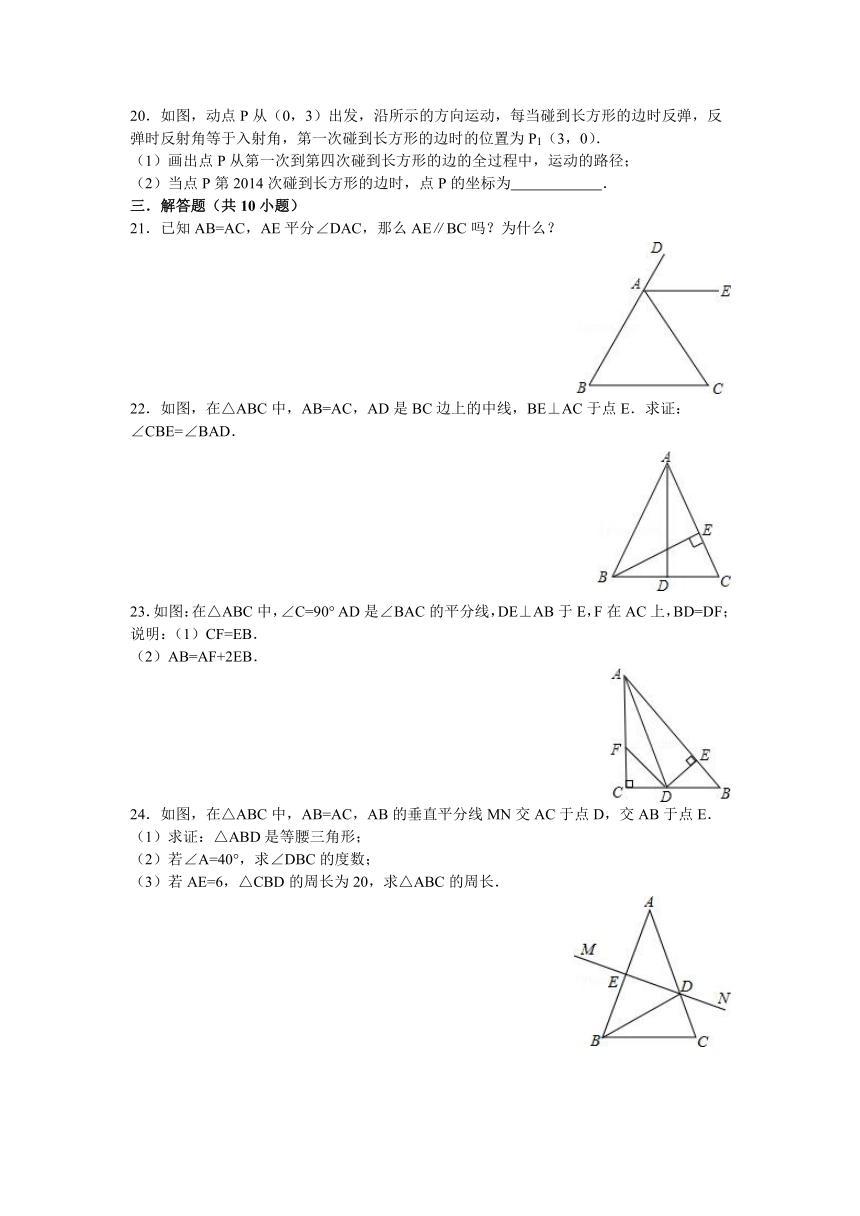
4.如图,△ABC与△DEF关于直线MN轴对称,则以下结论中错误的是( )
A.AB∥DF B.∠B=∠E
C.AB=DE D.AD的连线被MN垂直平分
5.如图,矩形ABCD中,E是AD的中点,将△ABE沿直线BE折叠后得到△GBE,延长BG交CD于点F.若AB=6,BC=4,则FD的长为( )
A.2 B.4 C. D.2
6.如图,点O是矩形ABCD的中心,E是AB上的点,沿CE折叠后,点B恰好与点O重合,若BC=3,则折痕CE的长为( )
A. B. C. D.6
7.如图,已知在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=5,DE=2,则△BCE的面积等于( )
A.10 B.7 C.5 D.4
8.如图,在△ABC中,∠C=90°,∠B=30°,AD是△ABC的角平分线,DE⊥AB,垂足为E,DE=1,则BC=( )
A. B.2 C.3 D.+2
(8题图) (9题图) (10题图)
9.如图,OC是∠AOB的平分线,P是OC上一点,PD⊥OA于点D,PD=6,则点P到边OB的距离为( )
A.6 B.5 C.4 D.3
10.如图,在△ABC中,AC=4cm,线段AB的垂直平分线交AC于点N,△BCN的周长是7cm,则BC的长为( )
A.1cm B.2cm C.3cm D.4cm
11.已知一个等腰三角形的两边长分别是2和4,则该等腰三角形的周长为( )
A.8或10 B.8 C.10 D.6或12
12.已知等腰三角形的一个内角为50°,则这个等腰三角形的顶角为( )
A.50° B.80° C.50°或80° D.40°或65°
13.已知a、b、c是三角形的三边长,且满足(a﹣b)2+|b﹣c|=0,那么这个三角形一定是( )
A.直角三角形 B.等边三角形 C.钝角三角形 D.锐角三角形
二.填空题(共7小题)
14.室内墙壁上挂一平面镜,明敏在平面镜内看到他背后墙上的时钟如图,则这时的实际时间是 .
(14题图) (15题图) (16题图) (17题图)
15.如图,点P是∠AOB外一点,点M、N分别是∠AOB两边上的点,点P关于OA的对称点Q恰好落在线段MN上,点P关于OB的对称点R落在线段MN的延长线上.若PM=2.5cm,PN=3cm,MN=4cm,则线段QR的长为 .
16.如图,在Rt△ABC中,∠C=90°,AD是△ABC的角平分线,DC=3,则点D到AB的距离是 .
17.如图,在△ABC中,∠C=31°,∠ABC的平分线BD交AC于点D,如果DE垂直平分BC,那么∠A= °.
18.等腰△ABC的底角为72°,腰AB的垂直平分线交另一腰AC于点E,垂足为D,连接BE,则∠EBC的度数为 .
(18题图) (19题图) (20题图)
19.已知:如图,△ABC中,BO,CO分别是∠ABC和∠ACB的平分线,过O点的直线分别交AB、AC于点D、E,且DE∥BC.若AB=6cm,AC=8cm,则△ADE的周长为 .
20.如图,动点P从(0,3)出发,沿所示的方向运动,每当碰到长方形的边时反弹,反弹时反射角等于入射角,第一次碰到长方形的边时的位置为P1(3,0).
(1)画出点P从第一次到第四次碰到长方形的边的全过程中,运动的路径;
(2)当点P第2014次碰到长方形的边时,点P的坐标为 .
三.解答题(共10小题)
21.已知AB=AC,AE平分∠DAC,那么AE∥BC吗?为什么?
22.如图,在△ABC中,AB=AC,AD是BC边上的中线,BE⊥AC于点E.求证:∠CBE=∠BAD.
23.如图:在△ABC中,∠C=90° AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF;
说明:(1)CF=EB.
(2)AB=AF+2EB.
24.如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,交AB于点E.
(1)求证:△ABD是等腰三角形;
(2)若∠A=40°,求∠DBC的度数;
(3)若AE=6,△CBD的周长为20,求△ABC的周长.
25.如图,AD∥BC,∠BAC=70°,DE⊥AC于点E,∠D=20°.
(1)求∠B的度数,并判断△ABC的形状;
(2)若延长线段DE恰好过点B,试说明DB是∠ABC的平分线.
26.如图,在平面直角坐标系中,A(﹣1,5),B(﹣1,0),C(﹣4,3).
(1)求出△ABC的面积;
(2)在图中作出△ABC关于y轴的对称图形△A1B1C1;
(3)写出点A1,B1,C1的坐标.
27.如图1是3×3的正方形方格,将其中两个方格涂黑,并且使涂黑后的整个图案是轴对称图形,(要求:绕正方形ABCD的中心旋转能重合的图案都视为同一种图案,例如图2中的四幅图就视为同一种图案),请在图3中的四幅图中完成你的设计.
28.如图已知:E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为C、D.求证:
(1)∠ECD=∠EDC;
(2)OE是CD的垂直平分线.
29.如图:A村和B村在公路l同侧,且AB=3千米,两村距离公路都是2千米.现决定在公路l上建立一个供水站P,要求使PA+PB最短.
(1)用尺规作图,作出点P; (作图要求:不写作法,保留作图痕迹)
(2)求出PA+PB的最小值.
30.如图,将长方形纸片ABCD沿对角线BD折叠得到△BDE,DE交AB于点G.
(1)求证:DG=BG;
(2)若AD=4,AB=8,求△BDG的面积.
鲁教版七年级数学上册期末总复习第2单元轴对称
参考答案
一.选择题(共13小题)
1.D; 2.C; 3.C; 4.A; 5.B; 6.A; 7.C; 8.C; 9.A; 10.C; 11.C; 12.C; 13.B;
二.填空题(共7小题)
14.3:40; 15.4.5cm; 16.3; 17.87; 18.36°; 19.14cm; 20.(5,0);
三.解答题(共10小题)
21.解:AE∥BC.
∵AB=AC,
∴∠B=∠C,
由三角形的外角性质得,∠DAC=∠B+∠C=2∠B,
∵AE平分∠DAC,
∴∠DAC=2∠DAE,
∴∠B=∠DAE,
∴AE∥BC.
22.证明:∵AB=AC,AD是BC边上的中线,BE⊥AC,
∴∠CBE+∠C=∠CAD+∠C=90°,∠CAD=∠BAD,
∴∠CBE=∠BAD.
23.证明:(1)∵AD是∠BAC的平分线,DE⊥AB,DC⊥AC,
∴DE=DC,
∵在Rt△DCF和Rt△DEB中,,
∴Rt△CDF≌Rt△EBD(HL).
∴CF=EB;
(2)∵AD是∠BAC的平分线,DE⊥AB,DC⊥AC,
∴CD=DE.
在△ADC与△ADE中,
∵
∴△ADC≌△ADE(HL),
∴AC=AE,
∴AB=AE+BE=AC+EB=AF+CF+EB=AF+2EB.
24.解:(1)证明:∵AB的垂直平分线MN交AC于点D,
∴DB=DA,
∴△ABD是等腰三角形;
(2)∵△ABD是等腰三角形,∠A=40°,
∴∠ABD=∠A=40°,∠ABC=∠C=(180°﹣40°)÷2=70°
∴∠DBC=∠ABC﹣∠ABD=70°﹣40°=30°;
(3)∵AB的垂直平分线MN交AC于点D,AE=6,
∴AB=2AE=12,
∵△CBD的周长为20,
∴AC+BC=20,
∴△ABC的周长=AB+AC+BC=12+20=32.
25.解:(1)∵DE⊥AC于点E,∠D=20°,
∴∠CAD=70°,
∵AD∥BC,
∴∠C=∠CAD=70°,
∵∠BAC=70°,
∴∠B=40°,AB=AC,
∴△ABC是等腰三角形;
(2)∵延长线段DE恰好过点B,DE⊥AC,
∴BD⊥AC,
∵△ABC是等腰三角形,
∴DB是∠ABC的平分线.
26.解:(1)如图所示:△ABC的面积:3×5﹣﹣﹣=6;
(2)如图所示:
(3)A1(2,5),B1(1,0),C1(4,3).
(26题图) (29题图)
27.解:如图所示.
28.证明:(1)∵E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,
∴EC=DE,
∴∠ECD=∠EDC;
(2)在Rt△OCE和Rt△ODE中,,∴Rt△OCE≌Rt△ODE(HL),
∵OE是∠AOB的平分线,
∴OE是CD的垂直平分线.
29.解:(1)作图,如右图,
作出A点的对称点A′,
连接BA′,找到交点P点;
(2)连接AB,由题意知AB=3km,A A′=4km,
在Rt△A A′B中,根据勾股定理得:A′B2=42+32,
∴A′B=5km,
即PA+PB=A′B=5km,
答:PA+PB的最小值是5km.
30.解:(1)由折叠可知∠CDB=∠GDB,
∵DC∥AB,
∴∠CDB=∠DBG.
∴∠GDB=∠DBG.
∴DG=BG.
(2)设DG=BG=x,则AG=8﹣x
在△ADG中,∠A=90°,
∴42+(8﹣x)2=x2.
解得x=5.
所以△BDG的面积=×5×4=10.
一.选择题(共13小题)
1.下面四个图形分别是节能、节水、低碳和绿色食品标志,在这四个标志中,是轴对称图形的是( )
A. B. C. D.
2.电子钟镜子里的像如图所示,实际时间是( )
A.21:10 B.10:21 C.10:51 D.12:01
(2题图) (4题图) (5题图) (6题图) (7题图)
3.下列图形中对称轴只有两条的是( )
A.B. C. D.
4.如图,△ABC与△DEF关于直线MN轴对称,则以下结论中错误的是( )
A.AB∥DF B.∠B=∠E
C.AB=DE D.AD的连线被MN垂直平分
5.如图,矩形ABCD中,E是AD的中点,将△ABE沿直线BE折叠后得到△GBE,延长BG交CD于点F.若AB=6,BC=4,则FD的长为( )
A.2 B.4 C. D.2
6.如图,点O是矩形ABCD的中心,E是AB上的点,沿CE折叠后,点B恰好与点O重合,若BC=3,则折痕CE的长为( )
A. B. C. D.6
7.如图,已知在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=5,DE=2,则△BCE的面积等于( )
A.10 B.7 C.5 D.4
8.如图,在△ABC中,∠C=90°,∠B=30°,AD是△ABC的角平分线,DE⊥AB,垂足为E,DE=1,则BC=( )
A. B.2 C.3 D.+2
(8题图) (9题图) (10题图)
9.如图,OC是∠AOB的平分线,P是OC上一点,PD⊥OA于点D,PD=6,则点P到边OB的距离为( )
A.6 B.5 C.4 D.3
10.如图,在△ABC中,AC=4cm,线段AB的垂直平分线交AC于点N,△BCN的周长是7cm,则BC的长为( )
A.1cm B.2cm C.3cm D.4cm
11.已知一个等腰三角形的两边长分别是2和4,则该等腰三角形的周长为( )
A.8或10 B.8 C.10 D.6或12
12.已知等腰三角形的一个内角为50°,则这个等腰三角形的顶角为( )
A.50° B.80° C.50°或80° D.40°或65°
13.已知a、b、c是三角形的三边长,且满足(a﹣b)2+|b﹣c|=0,那么这个三角形一定是( )
A.直角三角形 B.等边三角形 C.钝角三角形 D.锐角三角形
二.填空题(共7小题)
14.室内墙壁上挂一平面镜,明敏在平面镜内看到他背后墙上的时钟如图,则这时的实际时间是 .
(14题图) (15题图) (16题图) (17题图)
15.如图,点P是∠AOB外一点,点M、N分别是∠AOB两边上的点,点P关于OA的对称点Q恰好落在线段MN上,点P关于OB的对称点R落在线段MN的延长线上.若PM=2.5cm,PN=3cm,MN=4cm,则线段QR的长为 .
16.如图,在Rt△ABC中,∠C=90°,AD是△ABC的角平分线,DC=3,则点D到AB的距离是 .
17.如图,在△ABC中,∠C=31°,∠ABC的平分线BD交AC于点D,如果DE垂直平分BC,那么∠A= °.
18.等腰△ABC的底角为72°,腰AB的垂直平分线交另一腰AC于点E,垂足为D,连接BE,则∠EBC的度数为 .
(18题图) (19题图) (20题图)
19.已知:如图,△ABC中,BO,CO分别是∠ABC和∠ACB的平分线,过O点的直线分别交AB、AC于点D、E,且DE∥BC.若AB=6cm,AC=8cm,则△ADE的周长为 .
20.如图,动点P从(0,3)出发,沿所示的方向运动,每当碰到长方形的边时反弹,反弹时反射角等于入射角,第一次碰到长方形的边时的位置为P1(3,0).
(1)画出点P从第一次到第四次碰到长方形的边的全过程中,运动的路径;
(2)当点P第2014次碰到长方形的边时,点P的坐标为 .
三.解答题(共10小题)
21.已知AB=AC,AE平分∠DAC,那么AE∥BC吗?为什么?
22.如图,在△ABC中,AB=AC,AD是BC边上的中线,BE⊥AC于点E.求证:∠CBE=∠BAD.
23.如图:在△ABC中,∠C=90° AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF;
说明:(1)CF=EB.
(2)AB=AF+2EB.
24.如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,交AB于点E.
(1)求证:△ABD是等腰三角形;
(2)若∠A=40°,求∠DBC的度数;
(3)若AE=6,△CBD的周长为20,求△ABC的周长.
25.如图,AD∥BC,∠BAC=70°,DE⊥AC于点E,∠D=20°.
(1)求∠B的度数,并判断△ABC的形状;
(2)若延长线段DE恰好过点B,试说明DB是∠ABC的平分线.
26.如图,在平面直角坐标系中,A(﹣1,5),B(﹣1,0),C(﹣4,3).
(1)求出△ABC的面积;
(2)在图中作出△ABC关于y轴的对称图形△A1B1C1;
(3)写出点A1,B1,C1的坐标.
27.如图1是3×3的正方形方格,将其中两个方格涂黑,并且使涂黑后的整个图案是轴对称图形,(要求:绕正方形ABCD的中心旋转能重合的图案都视为同一种图案,例如图2中的四幅图就视为同一种图案),请在图3中的四幅图中完成你的设计.
28.如图已知:E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为C、D.求证:
(1)∠ECD=∠EDC;
(2)OE是CD的垂直平分线.
29.如图:A村和B村在公路l同侧,且AB=3千米,两村距离公路都是2千米.现决定在公路l上建立一个供水站P,要求使PA+PB最短.
(1)用尺规作图,作出点P; (作图要求:不写作法,保留作图痕迹)
(2)求出PA+PB的最小值.
30.如图,将长方形纸片ABCD沿对角线BD折叠得到△BDE,DE交AB于点G.
(1)求证:DG=BG;
(2)若AD=4,AB=8,求△BDG的面积.
鲁教版七年级数学上册期末总复习第2单元轴对称
参考答案
一.选择题(共13小题)
1.D; 2.C; 3.C; 4.A; 5.B; 6.A; 7.C; 8.C; 9.A; 10.C; 11.C; 12.C; 13.B;
二.填空题(共7小题)
14.3:40; 15.4.5cm; 16.3; 17.87; 18.36°; 19.14cm; 20.(5,0);
三.解答题(共10小题)
21.解:AE∥BC.
∵AB=AC,
∴∠B=∠C,
由三角形的外角性质得,∠DAC=∠B+∠C=2∠B,
∵AE平分∠DAC,
∴∠DAC=2∠DAE,
∴∠B=∠DAE,
∴AE∥BC.
22.证明:∵AB=AC,AD是BC边上的中线,BE⊥AC,
∴∠CBE+∠C=∠CAD+∠C=90°,∠CAD=∠BAD,
∴∠CBE=∠BAD.
23.证明:(1)∵AD是∠BAC的平分线,DE⊥AB,DC⊥AC,
∴DE=DC,
∵在Rt△DCF和Rt△DEB中,,
∴Rt△CDF≌Rt△EBD(HL).
∴CF=EB;
(2)∵AD是∠BAC的平分线,DE⊥AB,DC⊥AC,
∴CD=DE.
在△ADC与△ADE中,
∵
∴△ADC≌△ADE(HL),
∴AC=AE,
∴AB=AE+BE=AC+EB=AF+CF+EB=AF+2EB.
24.解:(1)证明:∵AB的垂直平分线MN交AC于点D,
∴DB=DA,
∴△ABD是等腰三角形;
(2)∵△ABD是等腰三角形,∠A=40°,
∴∠ABD=∠A=40°,∠ABC=∠C=(180°﹣40°)÷2=70°
∴∠DBC=∠ABC﹣∠ABD=70°﹣40°=30°;
(3)∵AB的垂直平分线MN交AC于点D,AE=6,
∴AB=2AE=12,
∵△CBD的周长为20,
∴AC+BC=20,
∴△ABC的周长=AB+AC+BC=12+20=32.
25.解:(1)∵DE⊥AC于点E,∠D=20°,
∴∠CAD=70°,
∵AD∥BC,
∴∠C=∠CAD=70°,
∵∠BAC=70°,
∴∠B=40°,AB=AC,
∴△ABC是等腰三角形;
(2)∵延长线段DE恰好过点B,DE⊥AC,
∴BD⊥AC,
∵△ABC是等腰三角形,
∴DB是∠ABC的平分线.
26.解:(1)如图所示:△ABC的面积:3×5﹣﹣﹣=6;
(2)如图所示:
(3)A1(2,5),B1(1,0),C1(4,3).
(26题图) (29题图)
27.解:如图所示.
28.证明:(1)∵E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,
∴EC=DE,
∴∠ECD=∠EDC;
(2)在Rt△OCE和Rt△ODE中,,∴Rt△OCE≌Rt△ODE(HL),
∵OE是∠AOB的平分线,
∴OE是CD的垂直平分线.
29.解:(1)作图,如右图,
作出A点的对称点A′,
连接BA′,找到交点P点;
(2)连接AB,由题意知AB=3km,A A′=4km,
在Rt△A A′B中,根据勾股定理得:A′B2=42+32,
∴A′B=5km,
即PA+PB=A′B=5km,
答:PA+PB的最小值是5km.
30.解:(1)由折叠可知∠CDB=∠GDB,
∵DC∥AB,
∴∠CDB=∠DBG.
∴∠GDB=∠DBG.
∴DG=BG.
(2)设DG=BG=x,则AG=8﹣x
在△ADG中,∠A=90°,
∴42+(8﹣x)2=x2.
解得x=5.
所以△BDG的面积=×5×4=10.
