2023-2024学年广东省湛江第一中学高一下学期期末考试数学试题(含答案)
文档属性
| 名称 | 2023-2024学年广东省湛江第一中学高一下学期期末考试数学试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 493.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-27 13:07:58 | ||
图片预览




文档简介
2023-2024学年广东省湛江第一中学高一下学期期末考试数学试题
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知,若为纯虚数,则( )
A. B. C. D.
2.下列说法正确的是( )
A. 棱柱中两个互相平行的平面一定是棱柱的底面
B. 棱柱的侧面都是全等的平行四边形
C. 有两个面平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行的几何体叫棱柱
D. 用一个平面去截棱锥,棱锥底面与截面之间的部分是棱台
3.某读书会有名成员,寒假期间他们每个人阅读的书本数分别如下:,,,,,,则这组数据的分位数为( )
A. B. C. D.
4.雷锋塔,位于浙江省杭州市西湖区,是“西湖十景”之一、中国九大名塔之一,为中国首座彩色铜雕宝塔如图,某同学为测量雷锋塔的高度,在雷锋塔的正西方向找到一座建筑物,高约为,在地面上点处三点共线测得建筑物顶部,雷锋塔顶部的仰角分别为和,在处测得塔顶部的仰角为,则雷锋塔的高度约为( )
A. B. C. D.
5.已知函数的部分图象如图所示,且,则( )
A. B.
C. D.
6.如图所示直三棱柱容器中,且,把容器装满水容器厚度忽略不计,将底面平放在桌面上,放水过程中当水面高度为的一半时,剩余水量与原来水量之比的比值为( )
A. B. C. D.
7.如图,已知四棱锥,底面是边长为的正方形,侧棱长相等且为,为的中点,则异面直线与所成的角的余弦值为( )
A. B. C. D.
8.在斜三角形中,角,,的对边分别为,,,,,点满足,且,则的面积为
A. B. C. D.
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.今年“五一”假期,各大商业综合体、超市等纷纷抓住节日商机,积极开展各类促销活动在某超市购买元以上商品的顾客可以参加一次抽奖活动,若顾客小王中奖的概率为,顾客小张中奖的概率为,则( )
A. 小王和小张都中奖的概率为
B. 小王和小张都没有中奖的概率为
C. 小王和小张中只有一个人中奖的概率为
D. 小王和小张中至多有一个人中奖的概率为
10.如图,已知圆锥,是底面圆的直径,点为圆周上的一个动点,圆锥的高与底面半径都等于,则下列说法正确的是( )
A. 圆锥的母线长为
B. 圆锥的母线与底面所成的角的余弦值为
C. 当三棱锥的体积最大时,
D. 若,则异面直线与所成的角的正弦值为
11.已知是所在平面内一点,则下列结论正确的是( )
A. 若,则为等腰三角形
B. 若,则为钝角三角形
C. 若为的垂心,,则
D. 若,则点的轨迹经过的重心
三、填空题:本题共3小题,每小题5分,共15分。
12.某市场有四类食品,其中粮食类、蔬菜类、肉类和水果类分别有种、种、种和种,现在从中抽取一个容量为的样本进行食品安全检测,若采用按比例分配的分层抽样的方法抽取样本,则抽取的粮食类和水果类的样本数之和为 .
13.已知,,则 .
14.已知是球的直径,,,是球面上两点,,,与平面所成的角为,则四面体的体积为 .
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
已知向量,,.
求在上的值域
求函数图象的对称中心坐标和对称轴方程.
16.本小题分
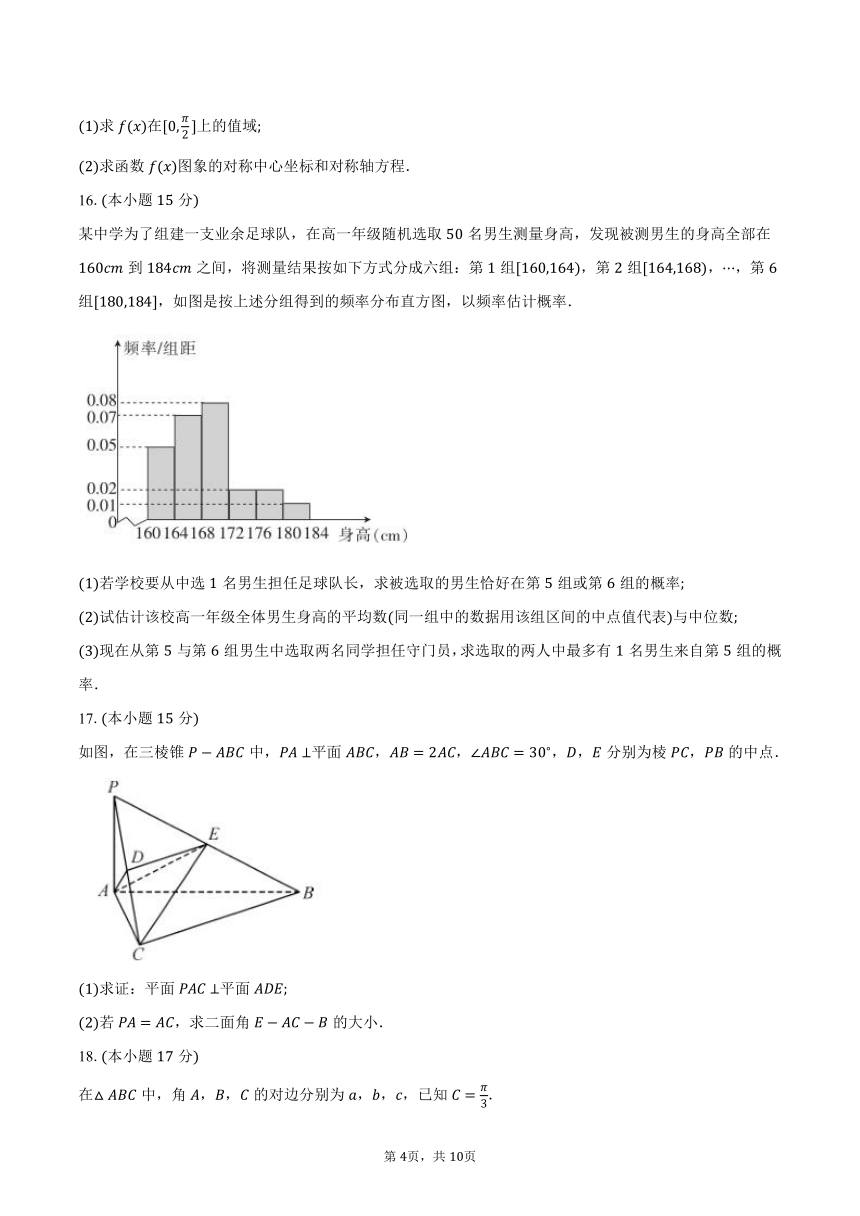
某中学为了组建一支业余足球队,在高一年级随机选取名男生测量身高,发现被测男生的身高全部在到之间,将测量结果按如下方式分成六组:第组,第组,,第组,如图是按上述分组得到的频率分布直方图,以频率估计概率.
若学校要从中选名男生担任足球队长,求被选取的男生恰好在第组或第组的概率
试估计该校高一年级全体男生身高的平均数同一组中的数据用该组区间的中点值代表与中位数
现在从第与第组男生中选取两名同学担任守门员,求选取的两人中最多有名男生来自第组的概率.
17.本小题分
如图,在三棱锥中,平面,,,,分别为棱,的中点.
求证:平面平面
若,求二面角的大小.
18.本小题分
在中,角,,的对边分别为,,,已知.
若,,的内角平分线交于点,求的长
若与的内角平分线相交于点,的外接圆半径为,求的最大值.
19.本小题分
如图,在三棱柱中,侧面为矩形.
设为中点,点在线段上,且,求证:平面;
若二面角的大小为,且,求直线和平面所成角的正弦值.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.解:由
当时,,
有,可得,故在上的值域为
令,,解得,,
可得函数图象的对称中心的坐标为,,
令,,解得,,
可得函数图象的对称轴方程为,
16.解:被选取的男生恰好在第组或第组的概率;
全体男生身高的平均数为:
,
设全体男生身高的中位数为,
因为第组对应的频率为,
第组对应的频率为,
所以,
则,
解得;
第组有人,记为,,,,
同理第组有人记为,,
所有的情况为、、、、
、、、
、、、、
、、、,共种,
选取的两人中最多有名男生来自第组的有、、、
、、、、、共种,
所以所求概率为.
17.证明: 平面 , 平面 ,
,
在 中, ,
由正弦定理 ,则 ,
,又 , 平面 ,
平面 ,又 分别为棱,的中点,
,则 平面 ,又 平面 ,
所以平面 平面 .
解:
如图,取 中点 ,连接 ,
又 为的中点, , ,
由 平面 , 平面 ,
又 平面 , ,
由知 , ,
平面 , ,
平面 ,又 平面 , ,
则 即为二面角 的平面角,
设 ,则 , ,
,
所以在直角三角形 中,
, ,
即二面角 的大小为 .
18.解:的内角平分线交于点,
,
,
,
;
如图,
的外接圆半径为,,
,
,,
与的内角平分线相交于点,
,即,
在中,由余弦定理得,,
,
,
,
,,
当且仅当时取等号,
的最大值为.
19.证明:连接交于,连接,
因为侧面为矩形,
所以,又为中点,
所以,
又因为,
所以.
所以,又平面,平面,
所以平面.
解:在平面中,过点作射线,
因为底面为矩形,所以,
所以为二面角的平面角,且.
又,,平面,所以平面,
在平面中,过点作,垂足为,连接,
因为平面,平面,
所以,又,平面,平面,
所以平面,
则即为直线和平面所成的角,
于是为点到平面的距离,且,
设直线和平面所成角为,又,
则,
所以直线和平面所成角的正弦值为.
第1页,共1页
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知,若为纯虚数,则( )
A. B. C. D.
2.下列说法正确的是( )
A. 棱柱中两个互相平行的平面一定是棱柱的底面
B. 棱柱的侧面都是全等的平行四边形
C. 有两个面平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行的几何体叫棱柱
D. 用一个平面去截棱锥,棱锥底面与截面之间的部分是棱台
3.某读书会有名成员,寒假期间他们每个人阅读的书本数分别如下:,,,,,,则这组数据的分位数为( )
A. B. C. D.
4.雷锋塔,位于浙江省杭州市西湖区,是“西湖十景”之一、中国九大名塔之一,为中国首座彩色铜雕宝塔如图,某同学为测量雷锋塔的高度,在雷锋塔的正西方向找到一座建筑物,高约为,在地面上点处三点共线测得建筑物顶部,雷锋塔顶部的仰角分别为和,在处测得塔顶部的仰角为,则雷锋塔的高度约为( )
A. B. C. D.
5.已知函数的部分图象如图所示,且,则( )
A. B.
C. D.
6.如图所示直三棱柱容器中,且,把容器装满水容器厚度忽略不计,将底面平放在桌面上,放水过程中当水面高度为的一半时,剩余水量与原来水量之比的比值为( )
A. B. C. D.
7.如图,已知四棱锥,底面是边长为的正方形,侧棱长相等且为,为的中点,则异面直线与所成的角的余弦值为( )
A. B. C. D.
8.在斜三角形中,角,,的对边分别为,,,,,点满足,且,则的面积为
A. B. C. D.
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.今年“五一”假期,各大商业综合体、超市等纷纷抓住节日商机,积极开展各类促销活动在某超市购买元以上商品的顾客可以参加一次抽奖活动,若顾客小王中奖的概率为,顾客小张中奖的概率为,则( )
A. 小王和小张都中奖的概率为
B. 小王和小张都没有中奖的概率为
C. 小王和小张中只有一个人中奖的概率为
D. 小王和小张中至多有一个人中奖的概率为
10.如图,已知圆锥,是底面圆的直径,点为圆周上的一个动点,圆锥的高与底面半径都等于,则下列说法正确的是( )
A. 圆锥的母线长为
B. 圆锥的母线与底面所成的角的余弦值为
C. 当三棱锥的体积最大时,
D. 若,则异面直线与所成的角的正弦值为
11.已知是所在平面内一点,则下列结论正确的是( )
A. 若,则为等腰三角形
B. 若,则为钝角三角形
C. 若为的垂心,,则
D. 若,则点的轨迹经过的重心
三、填空题:本题共3小题,每小题5分,共15分。
12.某市场有四类食品,其中粮食类、蔬菜类、肉类和水果类分别有种、种、种和种,现在从中抽取一个容量为的样本进行食品安全检测,若采用按比例分配的分层抽样的方法抽取样本,则抽取的粮食类和水果类的样本数之和为 .
13.已知,,则 .
14.已知是球的直径,,,是球面上两点,,,与平面所成的角为,则四面体的体积为 .
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
已知向量,,.
求在上的值域
求函数图象的对称中心坐标和对称轴方程.
16.本小题分
某中学为了组建一支业余足球队,在高一年级随机选取名男生测量身高,发现被测男生的身高全部在到之间,将测量结果按如下方式分成六组:第组,第组,,第组,如图是按上述分组得到的频率分布直方图,以频率估计概率.
若学校要从中选名男生担任足球队长,求被选取的男生恰好在第组或第组的概率
试估计该校高一年级全体男生身高的平均数同一组中的数据用该组区间的中点值代表与中位数
现在从第与第组男生中选取两名同学担任守门员,求选取的两人中最多有名男生来自第组的概率.
17.本小题分
如图,在三棱锥中,平面,,,,分别为棱,的中点.
求证:平面平面
若,求二面角的大小.
18.本小题分
在中,角,,的对边分别为,,,已知.
若,,的内角平分线交于点,求的长
若与的内角平分线相交于点,的外接圆半径为,求的最大值.
19.本小题分
如图,在三棱柱中,侧面为矩形.
设为中点,点在线段上,且,求证:平面;
若二面角的大小为,且,求直线和平面所成角的正弦值.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.解:由
当时,,
有,可得,故在上的值域为
令,,解得,,
可得函数图象的对称中心的坐标为,,
令,,解得,,
可得函数图象的对称轴方程为,
16.解:被选取的男生恰好在第组或第组的概率;
全体男生身高的平均数为:
,
设全体男生身高的中位数为,
因为第组对应的频率为,
第组对应的频率为,
所以,
则,
解得;
第组有人,记为,,,,
同理第组有人记为,,
所有的情况为、、、、
、、、
、、、、
、、、,共种,
选取的两人中最多有名男生来自第组的有、、、
、、、、、共种,
所以所求概率为.
17.证明: 平面 , 平面 ,
,
在 中, ,
由正弦定理 ,则 ,
,又 , 平面 ,
平面 ,又 分别为棱,的中点,
,则 平面 ,又 平面 ,
所以平面 平面 .
解:
如图,取 中点 ,连接 ,
又 为的中点, , ,
由 平面 , 平面 ,
又 平面 , ,
由知 , ,
平面 , ,
平面 ,又 平面 , ,
则 即为二面角 的平面角,
设 ,则 , ,
,
所以在直角三角形 中,
, ,
即二面角 的大小为 .
18.解:的内角平分线交于点,
,
,
,
;
如图,
的外接圆半径为,,
,
,,
与的内角平分线相交于点,
,即,
在中,由余弦定理得,,
,
,
,
,,
当且仅当时取等号,
的最大值为.
19.证明:连接交于,连接,
因为侧面为矩形,
所以,又为中点,
所以,
又因为,
所以.
所以,又平面,平面,
所以平面.
解:在平面中,过点作射线,
因为底面为矩形,所以,
所以为二面角的平面角,且.
又,,平面,所以平面,
在平面中,过点作,垂足为,连接,
因为平面,平面,
所以,又,平面,平面,
所以平面,
则即为直线和平面所成的角,
于是为点到平面的距离,且,
设直线和平面所成角为,又,
则,
所以直线和平面所成角的正弦值为.
第1页,共1页
同课章节目录
