华师大版七年级下册用加减法解二元一次方程组
文档属性
| 名称 | 华师大版七年级下册用加减法解二元一次方程组 |

|
|
| 格式 | rar | ||
| 文件大小 | 72.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-09-26 00:00:00 | ||
图片预览




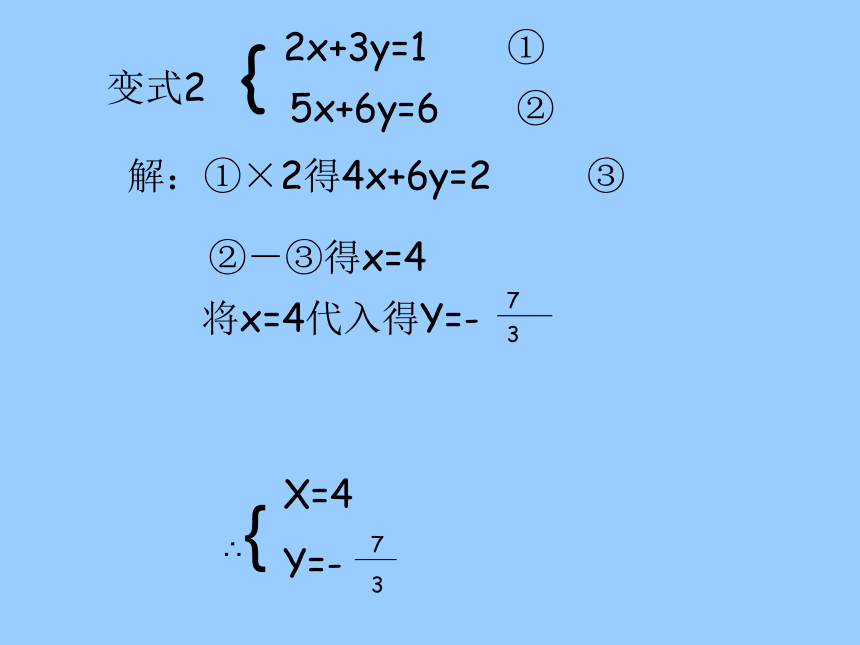

文档简介
课件13张PPT。欢迎各位 解法一:由(1)得: (3)把(3)代人(2)得解法二:由(1)得:3 y=1-2x (3)把(3)代人(2)得5x-(1-2x)=6
解法三:(1)+(2)得 : 7x=7 x=1把x=1代入(1)得 2+3y=1 试一试,有谁能用三种方法解?用加减法解二元一次方程组解题思路:消元
变式2:解方程组 2x+3y=1 (1)
5x+6y=6 (2)变式1:解方程组 2x+3y=1 (1)
5x+3y=6 (2)变式3:解方程组 ∴{变式2 {2x+3y=1 ①5x+6y=6 ②解:①×2得4x+6y=2 ③ ②-③得x=4将x=4代入得Y=-73X=4
Y=-73解法二:(1) ×5得:10x+15y=5 (3)(2) ×2得:10x–8y=12 (4)(3) – (4)得:23y = –7 把 代入(1)得, ∴ 加减法解二元一次方程组的一般步骤:4。写出方程组的解。
1。把一个方程(或两个方程)的两边都乘以一个适当的数,使两个方程的一个未知数的系数的绝对值相等;
2。把一个未知数系数绝对值相等的两个方程的两边分别相加(或相减),得到一个一元一次方程,求得一个未知数的值;
3。把这个未知数的值代入原方程组的任何一个方程,求得另一个未知数的值;
1.下列方程组各选择哪种消元法来解比较简便?(1) y=2x
3x-4y=5 x-2y=y+1
2x-3y=10(3) 2x+3y=21
4x-5y=7(4) 9x-5y=1
6x-7y=2代入法代入或加减法加减法加减法2.解下列二元一次方程组(1) 7x–3y=15 (2) 4s–15t=17
5x+6y–27=0 6s–25t=23 3、开放练习:写出一个二元一次方程组:满足条件:
(1)含有2个未知数x和y;(2)能用“加法”消去x,求出y。 3(x–1)=y+5
5(y–1)=3(x+5)
4、创新练习:(1)解方程组 2x+3y = 6 (1)
2 x–3y = –2 (2)解:(1)+(2)得 4x=4,x=1
(1)–(2)得 6y=8,y=
∴ x=1
y=(2)已知 3a+b=9 ,求16a–2b的值。
5a–2b=3解:两式相加得8a–b=12
∴ 16a–2b=2(8a–b)=2×12=24归纳小结1、解二元一次方程组的基本方法:加减法和代入法2、基本思路:消元3、加减法解方程组的一般步骤:(1)变换系数;(2)加减消元(同号减,异号加);
(3)回代求解;
(4)写出方程组的解。拓展延伸 能力题:1、解方程组: x+y+z=26
x–y=1
2x–y+z=182、在方程组 x+y=k 中,已知x>0,y<0,求正偶数k的值。
2x–y=6作业:
1、p24 1(2)(4)2(2)(4)
2。B 2再见
解法三:(1)+(2)得 : 7x=7 x=1把x=1代入(1)得 2+3y=1 试一试,有谁能用三种方法解?用加减法解二元一次方程组解题思路:消元
变式2:解方程组 2x+3y=1 (1)
5x+6y=6 (2)变式1:解方程组 2x+3y=1 (1)
5x+3y=6 (2)变式3:解方程组 ∴{变式2 {2x+3y=1 ①5x+6y=6 ②解:①×2得4x+6y=2 ③ ②-③得x=4将x=4代入得Y=-73X=4
Y=-73解法二:(1) ×5得:10x+15y=5 (3)(2) ×2得:10x–8y=12 (4)(3) – (4)得:23y = –7 把 代入(1)得, ∴ 加减法解二元一次方程组的一般步骤:4。写出方程组的解。
1。把一个方程(或两个方程)的两边都乘以一个适当的数,使两个方程的一个未知数的系数的绝对值相等;
2。把一个未知数系数绝对值相等的两个方程的两边分别相加(或相减),得到一个一元一次方程,求得一个未知数的值;
3。把这个未知数的值代入原方程组的任何一个方程,求得另一个未知数的值;
1.下列方程组各选择哪种消元法来解比较简便?(1) y=2x
3x-4y=5 x-2y=y+1
2x-3y=10(3) 2x+3y=21
4x-5y=7(4) 9x-5y=1
6x-7y=2代入法代入或加减法加减法加减法2.解下列二元一次方程组(1) 7x–3y=15 (2) 4s–15t=17
5x+6y–27=0 6s–25t=23 3、开放练习:写出一个二元一次方程组:满足条件:
(1)含有2个未知数x和y;(2)能用“加法”消去x,求出y。 3(x–1)=y+5
5(y–1)=3(x+5)
4、创新练习:(1)解方程组 2x+3y = 6 (1)
2 x–3y = –2 (2)解:(1)+(2)得 4x=4,x=1
(1)–(2)得 6y=8,y=
∴ x=1
y=(2)已知 3a+b=9 ,求16a–2b的值。
5a–2b=3解:两式相加得8a–b=12
∴ 16a–2b=2(8a–b)=2×12=24归纳小结1、解二元一次方程组的基本方法:加减法和代入法2、基本思路:消元3、加减法解方程组的一般步骤:(1)变换系数;(2)加减消元(同号减,异号加);
(3)回代求解;
(4)写出方程组的解。拓展延伸 能力题:1、解方程组: x+y+z=26
x–y=1
2x–y+z=182、在方程组 x+y=k 中,已知x>0,y<0,求正偶数k的值。
2x–y=6作业:
1、p24 1(2)(4)2(2)(4)
2。B 2再见
