六年级下册数学北师大版 反比例(课件)(共27张PPT)
文档属性
| 名称 | 六年级下册数学北师大版 反比例(课件)(共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-27 10:53:47 | ||
图片预览




文档简介
(共27张PPT)
北师大版 六年级下册 第四单元 正比例与反比例
(第1课时)
一、复习
1.什么叫成正比例的量?
两种( )的量,一种量变化,另一种量也( ),如果这两种量中相对应的两个数的( )(即 )一定,这两种量就叫做成正比例的量,它们的关系就是正比例关系。
2.正比例的关系式是什么?
如果用字母x和y表示两种相关联的量,用k表示它们的比值,正比例可以表示为( )。
两个数的商
随着变化
比值
相关联
3.判断下面各题中的两个量是否成正比例,是的在括号里画“√”,不是的画“×”,并说一说理由。
(1)白糖单价一定,白糖总价和重量。( )
(5)长方形的面积一定,它的长和宽。( )
(4)长方形的长一定,它的面积和宽。( )
(3)一个人的身高和体重。( )
(2)稻谷的出米率一定,碾成大米重量和稻谷 重量。( )
√
×
×
√
√
财主与帽子
古时候,有一个贪婪的财主,拿了一匹上好的布料准备做一顶帽子,到了裁缝店,觉得这样好的布料做- -项帽子似乎浪费了,于是问裁缝:“ 这匹布可以做两顶帽子吗 ”
裁缝看了看财主一眼,说:“可以。”
财主见他回答得那么爽快,心想,这裁缝肯定是从中占了些什么便宜,于是又问,“那做3顶帽子吗 ”
裁缝依然很爽快地说:“行!”
这时,财主更加疑惑了,嘀咕着:“多好的一-匹布啊,那我做4顶可以吗”“行!”裁缝仍然很快地回答。
经过一- 翻的较量后,财主最后问:“那我想做10顶帽子可以吗 ”
裁缝迟疑了一会,然后打量着财主,慢慢的说:“可以的。’
这时财主才放下心来,心想:这匹布料如果只做一顶帽子,那就便宜裁缝了。瞧!这不让我说到10顶了吧。我还真聪明!嘿....
过了几天,财主到了裁缝店取帽子,结果一看,顿时傻了眼: 10 顶的帽子小得只能戴在手指头.上了!
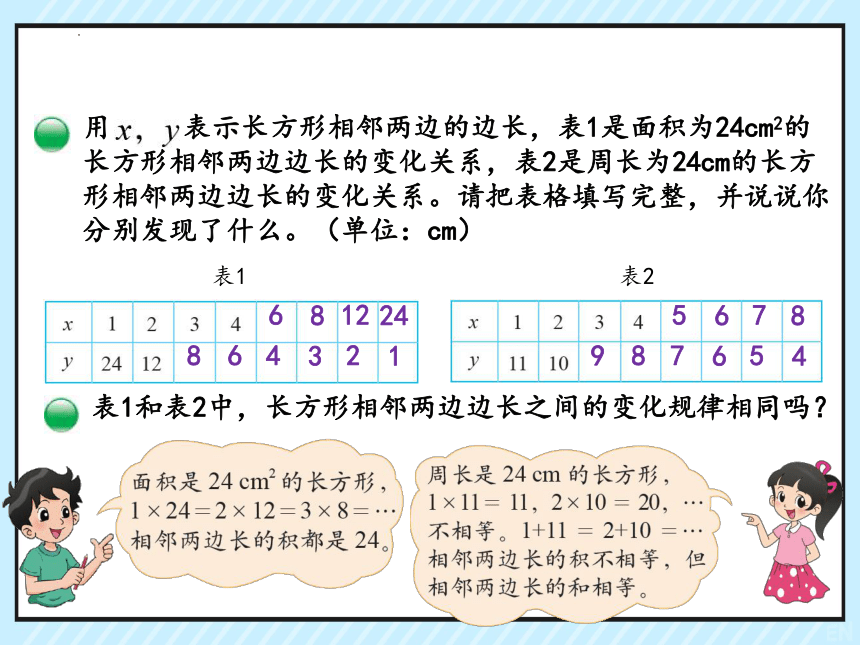
用 表示长方形相邻两边的边长,表1是面积为24cm2的长方形相邻两边边长的变化关系,表2是周长为24cm的长方形相邻两边边长的变化关系。请把表格填写完整,并说说你分别发现了什么。(单位:cm)
表1
表2
8
6
6
4
8
3
12
2
24
1
9
8
5
7
6
6
7
5
8
4
表1和表2中,长方形相邻两边边长之间的变化规律相同吗?
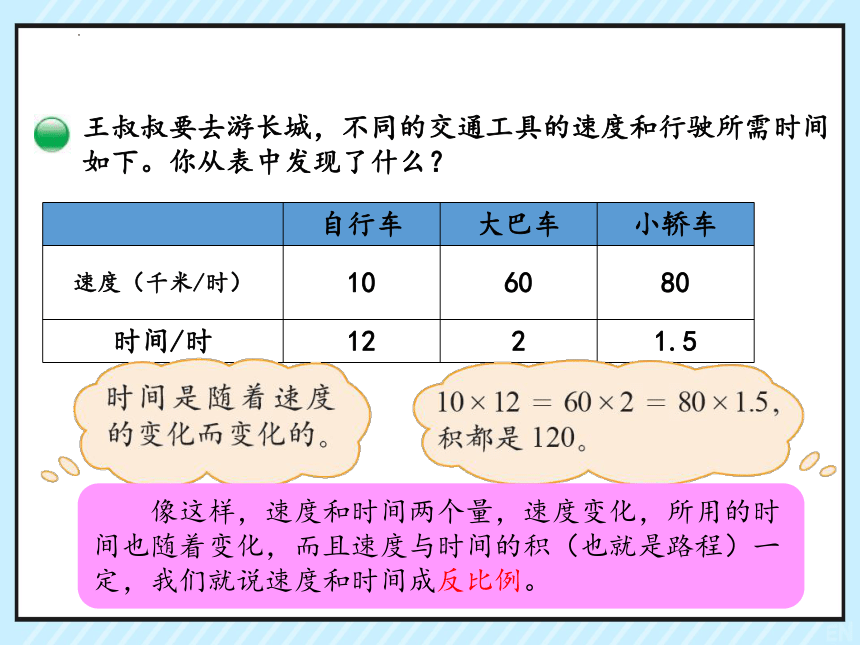
王叔叔要去游长城,不同的交通工具的速度和行驶所需时间如下。你从表中发现了什么?
自行车 大巴车 小轿车
速度(千米/时) 10 60 80
时间/时 12 2 1.5
像这样,速度和时间两个量,速度变化,所用的时间也随着变化,而且速度与时间的积(也就是路程)一定,我们就说速度和时间成反比例。
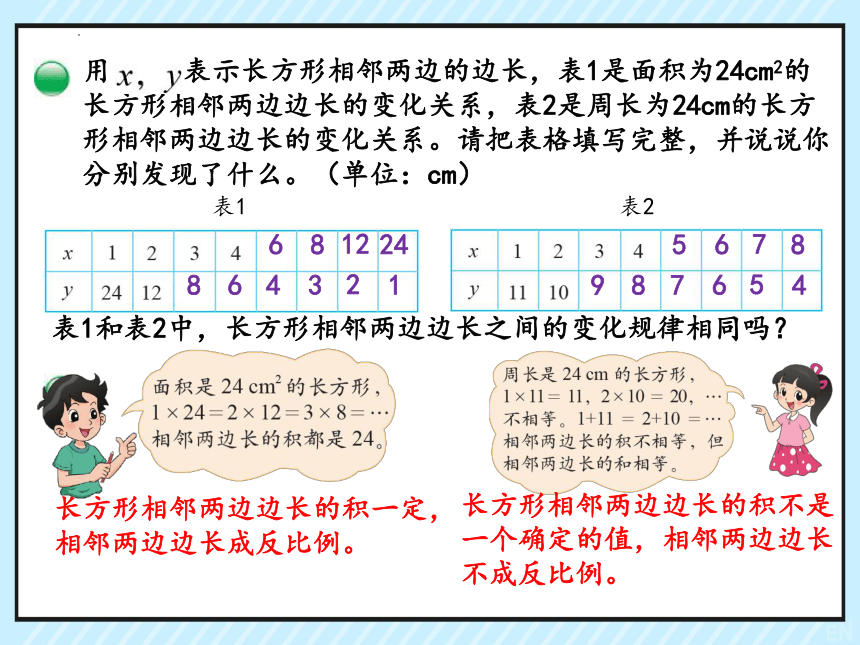
用 表示长方形相邻两边的边长,表1是面积为24cm2的长方形相邻两边边长的变化关系,表2是周长为24cm的长方形相邻两边边长的变化关系。请把表格填写完整,并说说你分别发现了什么。(单位:cm)
表1
表2
8
6
6
4
8
3
12
2
24
1
9
8
5
7
6
6
7
5
8
4
表1和表2中,长方形相邻两边边长之间的变化规律相同吗?
长方形相邻两边边长的积一定,相邻两边边长成反比例。
长方形相邻两边边长的积不是一个确定的值,相邻两边边长不成反比例。
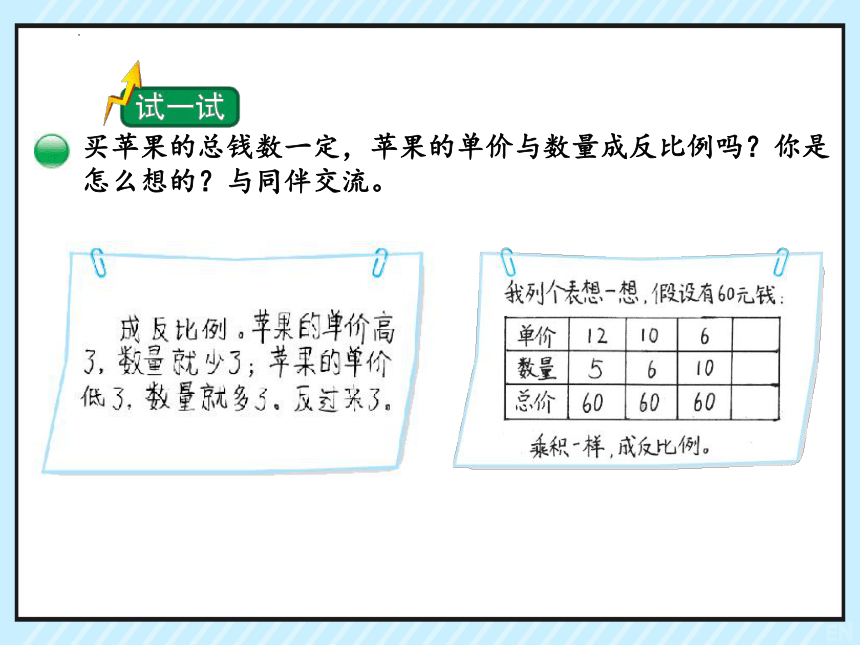
买苹果的总钱数一定,苹果的单价与数量成反比例吗?你是怎么想的?与同伴交流。
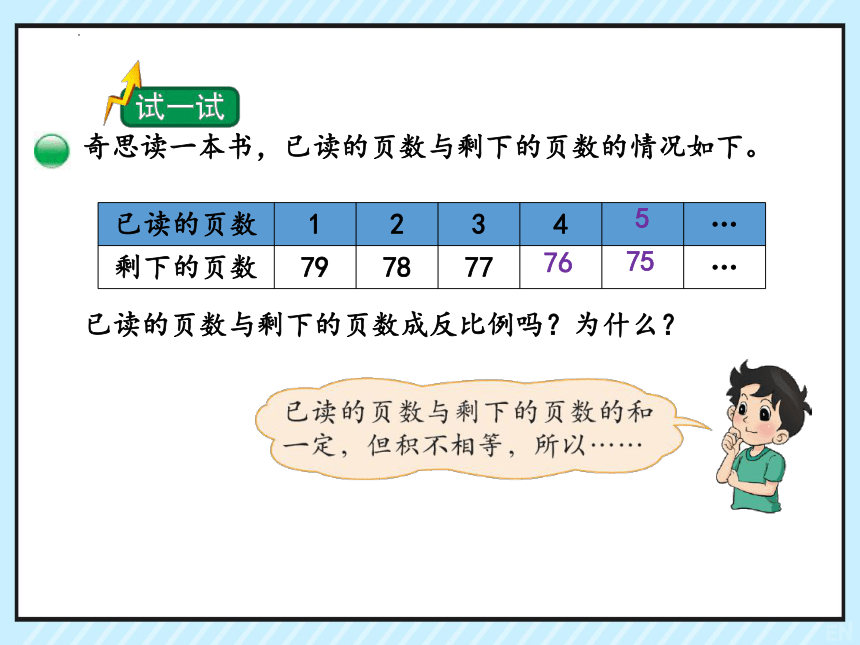
奇思读一本书,已读的页数与剩下的页数的情况如下。
已读的页数 1 2 3 4 …
剩下的页数 79 78 77 …
已读的页数与剩下的页数成反比例吗?为什么?
76
5
75
请举一个成反比例的例子,并与同伴交流。
⑴把上表补充完整。
⑵说一说看完全书所需天数与平均每天看的页数的变化关系。
⑶平均每天看的页数与看完全书所需天数是不是成反比例?
说明理由。
1.
平均每天看的页数 10 15 20 30 40
看完全书所需天数 12
8
6
4
3
成反比例,因为平均每天看的页数 看完全书所需天数=这本书的总页数
(一定)
2.电脑兴趣小组练习打同一份稿件,下表记录的是
每人打字所用的时间。
小敏 小峰 小英 小强
打字所用的时间/分 30 40 60 80
速度/(字/分) 80
请把上表补充完整,再回答下列问题。
⑴不同的人在打同一份稿件的过程中,哪个量没有变?
⑵打字的速度和所用的时间有什么关系?
⑶李老师打这份稿件用了24分,你知道她平均每分打
多少字吗?
60
40
30
总字数没变
成反比例
北师大版 六年级下册 第四单元 正比例与反比例
(第2课时)
一、复习
1.什么叫成反比例的量?
两种( )的量,一种量变化,另一种量也( ),如果这两种量中相对应的两个数的( )一定,这两种量就叫做成反比例的量,它们的关系就是反比例关系。
2.反比例的关系式是什么?
如果用字母x和y表示两种相关联的量,用k表示它们的比值,正比例可以表示为( )。
随着变化
积
相关联
(2)分母×分数值=分子,( )一定,( )和( )成反比例。
2.填一填。
(1) 每袋面粉的质量,( )一定,( )和( )成反比例。
每袋面粉的质量
总质量
总袋数
分子
分数值
分母
(3)小丽买一种笔记本,每本1.5元,可以买12本。如果用这些钱全部买另一种作业本,能买9本,每本( )元。题中( )和( )是两种相关联的量,( )是一定的量,两种相关联的量成( )比例。列出等式是( )。
(4)总价一定,( )和( )成反比例。
单价×数量=总价
2
单价
数量
总价
反
单价
数量
3.选一选,把正确答案的字母填在括号里。
(1)要运一堆粮食,每次运的质量和运的次数( )。
A.成正比例 B.成反比例 C.不成比例
(3)把一定量的水倒入长方体形状的容器里,水的高度和容器的底面积( )。
A.成反比例 B.成正比例 C.不成比例
(2)一袋米,吃去的质量和剩下的质量( )。
A.成反比例 B.成正比例 C.不成比例
B
A
C
(4)下列成反比例的是( )。
A.互为倒数的两个数
B.圆柱的高一定,体积和底面积
C.被减数一定,减数和差
(5)下列各组量中成反比例的是( )。
A.同时同地竿高和影长
B.正方形的周长和面积
C.积一定,两个因数
A
C
3.判断下面各题中的两个量是否成反比例,并说明
理由。
⑴行驶的路程一定,车轮的周长与车轮需要转动的圈数。
⑵一个人跑步的速度和他的体重。
⑶平行四边形的面积一定,它的底和高。
⑷笑笑从家步行到学校,已走的路程和剩下的路程。
成反比例
成反比例
不成反比例
不成反比例
4.截至2002年年底,我国探明可直接利用的煤炭储量为2298.86亿吨。我国煤炭年均开采量与可开采年数之间的关系如下表。
判断我国煤炭年均开采量与可开采年数之间是否成反比例,并说明理由。
成反比例
我国煤炭总开采量
(一定)
我们一定要节约煤炭资源
5.如图是两个互相啮合的齿轮,它们在同一时间内转动时,大齿轮和小齿轮转动的总齿数是相同的。尝试回答下面的问题。
⑴大齿轮和小齿轮在同一时间内转动
时,哪个齿轮转得更快?哪个齿轮
转的圈数多?
⑵转过的总齿数一定时,每个齿轮的
齿数和转过的圈数是什么关系?
⑶大齿轮有40个齿,小齿轮有24个齿。如果大齿轮每分转90圈,小齿轮每分转多少圈?
1.根据“工作效率×工作时间=工作总量”将下面的关系补充完整。
(1)( )一定,( )和( )成正比例
(2)( )一定,( )和( )成正比例。
(3)( )一定,( )和( )成反比例。
综合练习
2.一题多变,动脑筋解决。(在括号里填“成正比例”或“成反比例”)
(1)车轮的直径一定,所行的路程和车轮的转数( )。
(2)车轮的半径一定,所行的路程和车轮的转数( )。
(3)所行驶的路程一定,车轮的周长和车轮的转数( )。
(4)所行驶的路程一定,车轮的直径和车轮的转数( )。
(5)所行驶的路程一定,车轮的半径和车轮的转数( )。
(6)车轮的周长一定,所行驶的路程和车轮的转数( )。
(7)车轮的转数一定,所行驶的路程和车轮的周长( )。
成正比例
成正比例
成反比例
成反比例
成反比例
成正比例
成正比例
3.用一批纸装订练习本,每本有25页,可以装订400本。如果要装订500本,每本有x页。题中( )一定,关系式:( ) (一定),( )和( )成( )比例。
这批纸的总页数
装订本数
每本页数×装订本数=这批纸的总页数
每本页数
反
4.用边长为0.3m的正方形地砖铺一间会议室的地面,需要640块。如果改用边长为0.4m的正方形地砖,需要y块。题中( )一定,关系式:( )=( )(一定),( )和( )成( )比例。
反
会议室地面面积
每块地砖面积×块数
会议室地面面积
每块地砖面积
块数
北师大版 六年级下册 第四单元 正比例与反比例
(第1课时)
一、复习
1.什么叫成正比例的量?
两种( )的量,一种量变化,另一种量也( ),如果这两种量中相对应的两个数的( )(即 )一定,这两种量就叫做成正比例的量,它们的关系就是正比例关系。
2.正比例的关系式是什么?
如果用字母x和y表示两种相关联的量,用k表示它们的比值,正比例可以表示为( )。
两个数的商
随着变化
比值
相关联
3.判断下面各题中的两个量是否成正比例,是的在括号里画“√”,不是的画“×”,并说一说理由。
(1)白糖单价一定,白糖总价和重量。( )
(5)长方形的面积一定,它的长和宽。( )
(4)长方形的长一定,它的面积和宽。( )
(3)一个人的身高和体重。( )
(2)稻谷的出米率一定,碾成大米重量和稻谷 重量。( )
√
×
×
√
√
财主与帽子
古时候,有一个贪婪的财主,拿了一匹上好的布料准备做一顶帽子,到了裁缝店,觉得这样好的布料做- -项帽子似乎浪费了,于是问裁缝:“ 这匹布可以做两顶帽子吗 ”
裁缝看了看财主一眼,说:“可以。”
财主见他回答得那么爽快,心想,这裁缝肯定是从中占了些什么便宜,于是又问,“那做3顶帽子吗 ”
裁缝依然很爽快地说:“行!”
这时,财主更加疑惑了,嘀咕着:“多好的一-匹布啊,那我做4顶可以吗”“行!”裁缝仍然很快地回答。
经过一- 翻的较量后,财主最后问:“那我想做10顶帽子可以吗 ”
裁缝迟疑了一会,然后打量着财主,慢慢的说:“可以的。’
这时财主才放下心来,心想:这匹布料如果只做一顶帽子,那就便宜裁缝了。瞧!这不让我说到10顶了吧。我还真聪明!嘿....
过了几天,财主到了裁缝店取帽子,结果一看,顿时傻了眼: 10 顶的帽子小得只能戴在手指头.上了!
用 表示长方形相邻两边的边长,表1是面积为24cm2的长方形相邻两边边长的变化关系,表2是周长为24cm的长方形相邻两边边长的变化关系。请把表格填写完整,并说说你分别发现了什么。(单位:cm)
表1
表2
8
6
6
4
8
3
12
2
24
1
9
8
5
7
6
6
7
5
8
4
表1和表2中,长方形相邻两边边长之间的变化规律相同吗?
王叔叔要去游长城,不同的交通工具的速度和行驶所需时间如下。你从表中发现了什么?
自行车 大巴车 小轿车
速度(千米/时) 10 60 80
时间/时 12 2 1.5
像这样,速度和时间两个量,速度变化,所用的时间也随着变化,而且速度与时间的积(也就是路程)一定,我们就说速度和时间成反比例。
用 表示长方形相邻两边的边长,表1是面积为24cm2的长方形相邻两边边长的变化关系,表2是周长为24cm的长方形相邻两边边长的变化关系。请把表格填写完整,并说说你分别发现了什么。(单位:cm)
表1
表2
8
6
6
4
8
3
12
2
24
1
9
8
5
7
6
6
7
5
8
4
表1和表2中,长方形相邻两边边长之间的变化规律相同吗?
长方形相邻两边边长的积一定,相邻两边边长成反比例。
长方形相邻两边边长的积不是一个确定的值,相邻两边边长不成反比例。
买苹果的总钱数一定,苹果的单价与数量成反比例吗?你是怎么想的?与同伴交流。
奇思读一本书,已读的页数与剩下的页数的情况如下。
已读的页数 1 2 3 4 …
剩下的页数 79 78 77 …
已读的页数与剩下的页数成反比例吗?为什么?
76
5
75
请举一个成反比例的例子,并与同伴交流。
⑴把上表补充完整。
⑵说一说看完全书所需天数与平均每天看的页数的变化关系。
⑶平均每天看的页数与看完全书所需天数是不是成反比例?
说明理由。
1.
平均每天看的页数 10 15 20 30 40
看完全书所需天数 12
8
6
4
3
成反比例,因为平均每天看的页数 看完全书所需天数=这本书的总页数
(一定)
2.电脑兴趣小组练习打同一份稿件,下表记录的是
每人打字所用的时间。
小敏 小峰 小英 小强
打字所用的时间/分 30 40 60 80
速度/(字/分) 80
请把上表补充完整,再回答下列问题。
⑴不同的人在打同一份稿件的过程中,哪个量没有变?
⑵打字的速度和所用的时间有什么关系?
⑶李老师打这份稿件用了24分,你知道她平均每分打
多少字吗?
60
40
30
总字数没变
成反比例
北师大版 六年级下册 第四单元 正比例与反比例
(第2课时)
一、复习
1.什么叫成反比例的量?
两种( )的量,一种量变化,另一种量也( ),如果这两种量中相对应的两个数的( )一定,这两种量就叫做成反比例的量,它们的关系就是反比例关系。
2.反比例的关系式是什么?
如果用字母x和y表示两种相关联的量,用k表示它们的比值,正比例可以表示为( )。
随着变化
积
相关联
(2)分母×分数值=分子,( )一定,( )和( )成反比例。
2.填一填。
(1) 每袋面粉的质量,( )一定,( )和( )成反比例。
每袋面粉的质量
总质量
总袋数
分子
分数值
分母
(3)小丽买一种笔记本,每本1.5元,可以买12本。如果用这些钱全部买另一种作业本,能买9本,每本( )元。题中( )和( )是两种相关联的量,( )是一定的量,两种相关联的量成( )比例。列出等式是( )。
(4)总价一定,( )和( )成反比例。
单价×数量=总价
2
单价
数量
总价
反
单价
数量
3.选一选,把正确答案的字母填在括号里。
(1)要运一堆粮食,每次运的质量和运的次数( )。
A.成正比例 B.成反比例 C.不成比例
(3)把一定量的水倒入长方体形状的容器里,水的高度和容器的底面积( )。
A.成反比例 B.成正比例 C.不成比例
(2)一袋米,吃去的质量和剩下的质量( )。
A.成反比例 B.成正比例 C.不成比例
B
A
C
(4)下列成反比例的是( )。
A.互为倒数的两个数
B.圆柱的高一定,体积和底面积
C.被减数一定,减数和差
(5)下列各组量中成反比例的是( )。
A.同时同地竿高和影长
B.正方形的周长和面积
C.积一定,两个因数
A
C
3.判断下面各题中的两个量是否成反比例,并说明
理由。
⑴行驶的路程一定,车轮的周长与车轮需要转动的圈数。
⑵一个人跑步的速度和他的体重。
⑶平行四边形的面积一定,它的底和高。
⑷笑笑从家步行到学校,已走的路程和剩下的路程。
成反比例
成反比例
不成反比例
不成反比例
4.截至2002年年底,我国探明可直接利用的煤炭储量为2298.86亿吨。我国煤炭年均开采量与可开采年数之间的关系如下表。
判断我国煤炭年均开采量与可开采年数之间是否成反比例,并说明理由。
成反比例
我国煤炭总开采量
(一定)
我们一定要节约煤炭资源
5.如图是两个互相啮合的齿轮,它们在同一时间内转动时,大齿轮和小齿轮转动的总齿数是相同的。尝试回答下面的问题。
⑴大齿轮和小齿轮在同一时间内转动
时,哪个齿轮转得更快?哪个齿轮
转的圈数多?
⑵转过的总齿数一定时,每个齿轮的
齿数和转过的圈数是什么关系?
⑶大齿轮有40个齿,小齿轮有24个齿。如果大齿轮每分转90圈,小齿轮每分转多少圈?
1.根据“工作效率×工作时间=工作总量”将下面的关系补充完整。
(1)( )一定,( )和( )成正比例
(2)( )一定,( )和( )成正比例。
(3)( )一定,( )和( )成反比例。
综合练习
2.一题多变,动脑筋解决。(在括号里填“成正比例”或“成反比例”)
(1)车轮的直径一定,所行的路程和车轮的转数( )。
(2)车轮的半径一定,所行的路程和车轮的转数( )。
(3)所行驶的路程一定,车轮的周长和车轮的转数( )。
(4)所行驶的路程一定,车轮的直径和车轮的转数( )。
(5)所行驶的路程一定,车轮的半径和车轮的转数( )。
(6)车轮的周长一定,所行驶的路程和车轮的转数( )。
(7)车轮的转数一定,所行驶的路程和车轮的周长( )。
成正比例
成正比例
成反比例
成反比例
成反比例
成正比例
成正比例
3.用一批纸装订练习本,每本有25页,可以装订400本。如果要装订500本,每本有x页。题中( )一定,关系式:( ) (一定),( )和( )成( )比例。
这批纸的总页数
装订本数
每本页数×装订本数=这批纸的总页数
每本页数
反
4.用边长为0.3m的正方形地砖铺一间会议室的地面,需要640块。如果改用边长为0.4m的正方形地砖,需要y块。题中( )一定,关系式:( )=( )(一定),( )和( )成( )比例。
反
会议室地面面积
每块地砖面积×块数
会议室地面面积
每块地砖面积
块数
