人教版2024-2025学年度八年级上册数学第十三章 轴对称 单元测试卷(含答案)
文档属性
| 名称 | 人教版2024-2025学年度八年级上册数学第十三章 轴对称 单元测试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-27 00:00:00 | ||
图片预览


文档简介
人教版2024-2025学年度八年级上册数学单元测试卷
第十三章 轴对称
(本试卷三个大题,25个小题。满分150分,考试时间120分钟。)
一、选择题(本题共12个小题,每小题3分,共36分;每个小题A、B、C、D四选项,只有一项符合题意。)
1.下列图形中,为轴对称图形的是( )
A. B. C. D.
2.以下列各组数据为边长,可以构成等腰三角形的是( )
A.2,3,4 B.5,5,10 C.2,2,1 D.1,2,3
3.若等腰三角形的一个外角等于,则它的底角的度数为( )
A. B. C. D.或
4.如图,把长方形沿对折,若,则等于( )
A. B. C. D.
5.如图,在△ABC中,AB=AC,AD⊥BC,∠B=30°,则∠CAD的度数为( )
A.30° B.60° C.90° D.120°
6.等腰三角形的周长为10cm,其中一边长为4cm,则该等腰三角形的底边长为( )
A.5cm B.4cm C.3cm或4cm D.2cm或4cm
7.已知:如图,P、Q是△ABC的边BC上的两点,,并且PB=PQ=QC=AP=AQ.则∠BAQ=( )
A.90° B.40° C.60° D.70°
8.已知:在△ABC中,AB=AC,O为不同于A的一点,且OB=OC,则直线AO与底边BC的关系为( )
A.平行 B.AO垂直且平分BC C.斜交 D.AO垂直但不平分BC
9.如图,在中,,,D是的中点,于D,交于E,则的度数是( )
A. B.
C. D.
10.如图,与关于直线l对称,连接,,,其中分别交,于点D,,下列结论:①;②;③直线l垂直平分;④直线与的交点不一定在直线l上.其中正确的是( )
A.①②③ B.②③④ C.①②④ D.①③④
11.如图,AD平分,BD平分,于E,交ED的延长线于点F,给出以下三个结论:①;②;③,其中正确的结论共有( )
A.0个 B.3个 C.2个 D.1个
12.如图,在等边中;在、上分别截取、,使.再分别以点P,Q为圆心,以大于的长为半径作弧,两弧在内交于点R,作射线,交于点D.已知,.若点M、N分别是线段和线段上的动点,则的最小值为( )
A. B. C. D.6
填空题(本题共4个小题,每小题4分,共16分。)
13.在平面直角坐标系中,点关于轴对称的点的坐标为 .
14.若一个等腰三角形的顶角为,则这个等腰三角形的底角为 .
15.若点与点关于轴对称,则的值为 .
16.如图所示,把一个长方形纸片沿折叠后,点D,C分别落在的位置.若,则 .
三、解答题(本题共9个小题,共98分。)
17.(8分)已知,,是的三边长.
(1)若,,满足,试判断的形状;(4分)
(2)化简:.(4分)
18.(10分)如图,B、E、C、F是直线l上的四点,相交于点G,,,.
(1)求证:是等腰三角形;(5分)
(2)连接,则与l的位置关系是________.(5分)
19.(10分)如图,在平面直角坐标系中,的三个顶点均在正方形网格的格点上.
(1)请你在图中画出关于y轴的对称图形,其中,顶点的坐标为______. (5分)
(2)的面积为______.(5分)
20.(10分)如图,已知和,,,,与交于点P,点C在上.
(1)求证:; (5分)
(2)若,,求的度数.(5分)
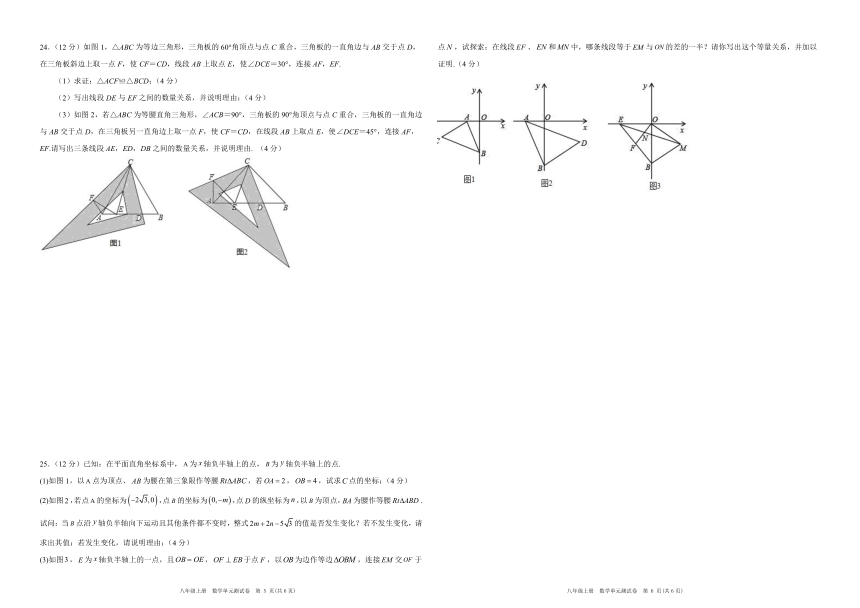
21.(12分)如图,在平面直角坐标系中
(1)做出△ABC关于y轴对称的,并求出三个顶点的坐标;(4分)
(2)计算△ABC的面积;(4分)
(3)在x轴上画点P,使PA+PC最小.(4分)
22.(12分)如图,,垂足为F.
(1)求证:;(4分)
(2)若,求四边形的面积;(4分)
(3)求的度数.(4分)
23.(12分)如图,平面直角坐标系中,,点在第一象限内,点在轴正半轴上,点在轴负半轴上,且,点坐标为,且满足,请解答下列问题:
(1)求点B和点C的坐标;(4分)
(2)若连接交y轴于点D,且,,求点A的坐标;(4分)
(3)在(2)的条件下,,在坐标轴上是否存在点E,使是以为腰的等腰三角形?若存在,请写出点E的个数,并直接写出其中3个点E的坐标;若不存在,请说明理由.(4分)
24.(12分)如图1,△ABC为等边三角形,三角板的60°角顶点与点C重合,三角板的一直角边与AB交于点D,在三角板斜边上取一点F,使CF=CD,线段AB上取点E,使∠DCE=30°,连接AF,EF.
(1)求证:△ACF≌△BCD;(4分)
(2)写出线段DE与EF之间的数量关系,并说明理由;(4分)
(3)如图2,若△ABC为等腰直角三角形,∠ACB=90°,三角板的90°角顶点与点C重合,三角板的一直角边与AB交于点D,在三角板另一直角边上取一点F,使CF=CD,在线段AB上取点E,使∠DCE=45°,连接AF,EF.请写出三条线段AE,ED,DB之间的数量关系,并说明理由. (4分)
25.(12分)已知:在平面直角坐标系中,为轴负半轴上的点,为轴负半轴上的点.
(1)如图1,以点为顶点、为腰在第三象限作等腰,若,,试求点的坐标;(4分)
(2)如图,若点的坐标为,点的坐标为,点的纵坐标为,以为顶点,为腰作等腰.试问:当点沿轴负半轴向下运动且其他条件都不变时,整式的值是否发生变化?若不发生变化,请求出其值;若发生变化,请说明理由;(4分)
(3)如图,为轴负半轴上的一点,且,于点,以为边作等边,连接交于点,试探索:在线段、和中,哪条线段等于与的差的一半?请你写出这个等量关系,并加以
证明.(4分)
试卷第1页,共3页
八年级上册 数学单元测试卷 第 1 页(共6页) 八年级上册 数学单元测试卷 第 1 页(共6页)
参考答案
一、选择题(本题共12个小题,每小题3分,共36分;每个小题A、B、C、D四选项,只有一项符合题意。)
1.B 2.C 3.C 4.D 5.B 6.D
7.A 8.B 9.C 10.A 11.B 12.C
二、填空题(本题共4个小题,每小题4分,共16分。)
13. 14.55 15. 16./70度
三、解答题(本题共9个小题,共98分。)
17.(1)等边三角形; (2).
【详解】(1)∵,
∴且,
∴,,
∴,
∴为等边三角形;
(2)∵,,是的三边长,
∴,,
∴.
18.(1)见解析 (2)
【详解】(1)证明:在和中
,
∴,
∴,
∴,
∴是等腰三角形;
(2)∵,,
∴,
∴,
∴,
∵,
∵,
∴,
∴.
19.(1)作图见解析, (2)9
【详解】(1)解:如图,即为所求,顶点的坐标为,
故答案为:;
(2)解:,
故答案为:9.
20.(1)见解析 (2)
【详解】(1)证明:∵,
∴,即,
在和中,
,
∴,
∴;
(2)解:∵,,
∴,
∵,
∴,
∴.
21.(1);(2)2.5;(3)见解析
【详解】解:(1)如图所示:
(2)如图,将补成矩形,则
,,,,,,,,
(3)如图所示
22.(1)证明过程见详解 (2)四边形的面积为32 (3)的度数为
【详解】(1)证明:∵,即,
∴,且,
∴;
(2)解:∵,且,
则,
∴,
∵,
∴,
∴四边形的面积为32;
(3)解:已知,
∴,
∵,
∴,
∵,即,
∴,
∴,
∴的度数为.
23.(1),; (2);
(3)存在,点E共有6个,;;;;;.
【详解】(1)解:
,点坐标为
,点坐标为
(2),
点的坐标
(3)在坐标轴上存在6个点,使是以为腰的等腰三角形
轴正半轴上使得,,
点关于轴的对称点
轴正半轴上使得,
轴负半轴上使得,
点关于轴的对称点
故坐标轴上存在6个点,;;;;;.
24.详见解析
详解:(1)∵△ABC是等边三角形,
∴AC=BC,∠BAC=∠B=∠BCA =60°,
∵∠DCF=60°,
∴∠ACF=∠BCD,
在△ACF和△BCD中,
,
∴△ACF≌△BCD(SAS);
(2)DE=EF.理由如下:
∵∠DCF=60°,∠DCE=30°,
∴∠FCE=60°﹣30°=30°,
∴∠DCE=∠FCE,
在△DCE和△FCE中,
,
∴△DCE≌△FCE(SAS),
∴DE=EF;
(3)AE2+DB2=DE2.理由如下:
∵△ABC是等腰直角三角形,∠ACB=90°,
∴AC=BC,∠BAC=∠B=45°.
∵∠DCF=90°,
∴∠ACF=∠BCD.
∵CF=CD,
∴△ACF≌△BCD(SAS),
∴∠CAF=∠B=45°,AF=DB,
∴∠EAF=∠BAC+∠CAF=90°;
∵∠DCF=90°,∠DCE=45°,
∴∠FCE=90°﹣45°=45°,
∴∠DCE=∠FCE,
在△DCE和△FCE中,,
∴△DCE≌△FCE(SAS),
∴DE=EF,
在Rt△AEF中,AE2+AF2=EF2,
又∵AF=DB,
∴AE2+DB2=DE2.
25.(1) C(-6,-2);(2)不发生变化,值为;(3)EN=(EM-ON),证明见详解.
【详解】(1)如图(1)作CQ⊥OA于Q,
∴∠AQC=90°,
∵为等腰直角三角形,
∴AC=AB,∠CAB=90°,
∴∠QAC+∠OAB=90°,
∵∠QAC+∠ACQ=90°,
∴∠ACQ=∠BAO,
又∵AC=AB,∠AQC=∠AOB,
∴(AAS),
∴CQ=AO,AQ=BO,
∵OA=2,OB=4,
∴CQ=2,AQ=4,
∴OQ=6,
∴C(-6,-2).
(2)如图(2)作DP⊥OB于点P,
∴∠BPD=90°,
∵是等腰直角三角形,
∴AB=BD,∠ABD=∠ABO+∠OBD=90°,
∵∠OBD+∠BDP=90°,
∴∠ABO=∠BDP,
又∵AB=BD,∠AOB=∠BPD=90°,
∴
∴AO=BP,
∵BP=OB-PO=m-(-n)=m+n,
∵A,
∴OA=,
∴m+n=,
∴当点B沿y轴负半轴向下运动时,AO=BP=m+n=,
∴整式的值不变为.
(3)
证明:如图(3)所示,在ME上取一点G使得MG=ON,连接BG并延长,交x轴于H.
∵为等边三角形,
∴BO=BM=MO,∠OBM=∠OMB=∠BOM=60°,
∴EO=MO,∠EBM=105°,∠1=30°,
∵OE=OB,
∴OE=OM=BM,
∴∠3=∠EMO=15°,
∴∠BEM=30°,∠BME=45°,
∵OF⊥EB,
∴∠EOF=∠BME,
∴,
∴BG=EN,
∵ON=MG,
∴∠2=∠3,
∴∠2=15°,
∴∠EBG=90°,
∴BG=EG,
∴EN=EG,
∵EG=EM-GM,
∴EN=(EM-GM),
∴EN=(EM-ON).
答案第1页,共2页
答案 第1页,共6页 答案 第1页,共6页
第十三章 轴对称
(本试卷三个大题,25个小题。满分150分,考试时间120分钟。)
一、选择题(本题共12个小题,每小题3分,共36分;每个小题A、B、C、D四选项,只有一项符合题意。)
1.下列图形中,为轴对称图形的是( )
A. B. C. D.
2.以下列各组数据为边长,可以构成等腰三角形的是( )
A.2,3,4 B.5,5,10 C.2,2,1 D.1,2,3
3.若等腰三角形的一个外角等于,则它的底角的度数为( )
A. B. C. D.或
4.如图,把长方形沿对折,若,则等于( )
A. B. C. D.
5.如图,在△ABC中,AB=AC,AD⊥BC,∠B=30°,则∠CAD的度数为( )
A.30° B.60° C.90° D.120°
6.等腰三角形的周长为10cm,其中一边长为4cm,则该等腰三角形的底边长为( )
A.5cm B.4cm C.3cm或4cm D.2cm或4cm
7.已知:如图,P、Q是△ABC的边BC上的两点,,并且PB=PQ=QC=AP=AQ.则∠BAQ=( )
A.90° B.40° C.60° D.70°
8.已知:在△ABC中,AB=AC,O为不同于A的一点,且OB=OC,则直线AO与底边BC的关系为( )
A.平行 B.AO垂直且平分BC C.斜交 D.AO垂直但不平分BC
9.如图,在中,,,D是的中点,于D,交于E,则的度数是( )
A. B.
C. D.
10.如图,与关于直线l对称,连接,,,其中分别交,于点D,,下列结论:①;②;③直线l垂直平分;④直线与的交点不一定在直线l上.其中正确的是( )
A.①②③ B.②③④ C.①②④ D.①③④
11.如图,AD平分,BD平分,于E,交ED的延长线于点F,给出以下三个结论:①;②;③,其中正确的结论共有( )
A.0个 B.3个 C.2个 D.1个
12.如图,在等边中;在、上分别截取、,使.再分别以点P,Q为圆心,以大于的长为半径作弧,两弧在内交于点R,作射线,交于点D.已知,.若点M、N分别是线段和线段上的动点,则的最小值为( )
A. B. C. D.6
填空题(本题共4个小题,每小题4分,共16分。)
13.在平面直角坐标系中,点关于轴对称的点的坐标为 .
14.若一个等腰三角形的顶角为,则这个等腰三角形的底角为 .
15.若点与点关于轴对称,则的值为 .
16.如图所示,把一个长方形纸片沿折叠后,点D,C分别落在的位置.若,则 .
三、解答题(本题共9个小题,共98分。)
17.(8分)已知,,是的三边长.
(1)若,,满足,试判断的形状;(4分)
(2)化简:.(4分)
18.(10分)如图,B、E、C、F是直线l上的四点,相交于点G,,,.
(1)求证:是等腰三角形;(5分)
(2)连接,则与l的位置关系是________.(5分)
19.(10分)如图,在平面直角坐标系中,的三个顶点均在正方形网格的格点上.
(1)请你在图中画出关于y轴的对称图形,其中,顶点的坐标为______. (5分)
(2)的面积为______.(5分)
20.(10分)如图,已知和,,,,与交于点P,点C在上.
(1)求证:; (5分)
(2)若,,求的度数.(5分)
21.(12分)如图,在平面直角坐标系中
(1)做出△ABC关于y轴对称的,并求出三个顶点的坐标;(4分)
(2)计算△ABC的面积;(4分)
(3)在x轴上画点P,使PA+PC最小.(4分)
22.(12分)如图,,垂足为F.
(1)求证:;(4分)
(2)若,求四边形的面积;(4分)
(3)求的度数.(4分)
23.(12分)如图,平面直角坐标系中,,点在第一象限内,点在轴正半轴上,点在轴负半轴上,且,点坐标为,且满足,请解答下列问题:
(1)求点B和点C的坐标;(4分)
(2)若连接交y轴于点D,且,,求点A的坐标;(4分)
(3)在(2)的条件下,,在坐标轴上是否存在点E,使是以为腰的等腰三角形?若存在,请写出点E的个数,并直接写出其中3个点E的坐标;若不存在,请说明理由.(4分)
24.(12分)如图1,△ABC为等边三角形,三角板的60°角顶点与点C重合,三角板的一直角边与AB交于点D,在三角板斜边上取一点F,使CF=CD,线段AB上取点E,使∠DCE=30°,连接AF,EF.
(1)求证:△ACF≌△BCD;(4分)
(2)写出线段DE与EF之间的数量关系,并说明理由;(4分)
(3)如图2,若△ABC为等腰直角三角形,∠ACB=90°,三角板的90°角顶点与点C重合,三角板的一直角边与AB交于点D,在三角板另一直角边上取一点F,使CF=CD,在线段AB上取点E,使∠DCE=45°,连接AF,EF.请写出三条线段AE,ED,DB之间的数量关系,并说明理由. (4分)
25.(12分)已知:在平面直角坐标系中,为轴负半轴上的点,为轴负半轴上的点.
(1)如图1,以点为顶点、为腰在第三象限作等腰,若,,试求点的坐标;(4分)
(2)如图,若点的坐标为,点的坐标为,点的纵坐标为,以为顶点,为腰作等腰.试问:当点沿轴负半轴向下运动且其他条件都不变时,整式的值是否发生变化?若不发生变化,请求出其值;若发生变化,请说明理由;(4分)
(3)如图,为轴负半轴上的一点,且,于点,以为边作等边,连接交于点,试探索:在线段、和中,哪条线段等于与的差的一半?请你写出这个等量关系,并加以
证明.(4分)
试卷第1页,共3页
八年级上册 数学单元测试卷 第 1 页(共6页) 八年级上册 数学单元测试卷 第 1 页(共6页)
参考答案
一、选择题(本题共12个小题,每小题3分,共36分;每个小题A、B、C、D四选项,只有一项符合题意。)
1.B 2.C 3.C 4.D 5.B 6.D
7.A 8.B 9.C 10.A 11.B 12.C
二、填空题(本题共4个小题,每小题4分,共16分。)
13. 14.55 15. 16./70度
三、解答题(本题共9个小题,共98分。)
17.(1)等边三角形; (2).
【详解】(1)∵,
∴且,
∴,,
∴,
∴为等边三角形;
(2)∵,,是的三边长,
∴,,
∴.
18.(1)见解析 (2)
【详解】(1)证明:在和中
,
∴,
∴,
∴,
∴是等腰三角形;
(2)∵,,
∴,
∴,
∴,
∵,
∵,
∴,
∴.
19.(1)作图见解析, (2)9
【详解】(1)解:如图,即为所求,顶点的坐标为,
故答案为:;
(2)解:,
故答案为:9.
20.(1)见解析 (2)
【详解】(1)证明:∵,
∴,即,
在和中,
,
∴,
∴;
(2)解:∵,,
∴,
∵,
∴,
∴.
21.(1);(2)2.5;(3)见解析
【详解】解:(1)如图所示:
(2)如图,将补成矩形,则
,,,,,,,,
(3)如图所示
22.(1)证明过程见详解 (2)四边形的面积为32 (3)的度数为
【详解】(1)证明:∵,即,
∴,且,
∴;
(2)解:∵,且,
则,
∴,
∵,
∴,
∴四边形的面积为32;
(3)解:已知,
∴,
∵,
∴,
∵,即,
∴,
∴,
∴的度数为.
23.(1),; (2);
(3)存在,点E共有6个,;;;;;.
【详解】(1)解:
,点坐标为
,点坐标为
(2),
点的坐标
(3)在坐标轴上存在6个点,使是以为腰的等腰三角形
轴正半轴上使得,,
点关于轴的对称点
轴正半轴上使得,
轴负半轴上使得,
点关于轴的对称点
故坐标轴上存在6个点,;;;;;.
24.详见解析
详解:(1)∵△ABC是等边三角形,
∴AC=BC,∠BAC=∠B=∠BCA =60°,
∵∠DCF=60°,
∴∠ACF=∠BCD,
在△ACF和△BCD中,
,
∴△ACF≌△BCD(SAS);
(2)DE=EF.理由如下:
∵∠DCF=60°,∠DCE=30°,
∴∠FCE=60°﹣30°=30°,
∴∠DCE=∠FCE,
在△DCE和△FCE中,
,
∴△DCE≌△FCE(SAS),
∴DE=EF;
(3)AE2+DB2=DE2.理由如下:
∵△ABC是等腰直角三角形,∠ACB=90°,
∴AC=BC,∠BAC=∠B=45°.
∵∠DCF=90°,
∴∠ACF=∠BCD.
∵CF=CD,
∴△ACF≌△BCD(SAS),
∴∠CAF=∠B=45°,AF=DB,
∴∠EAF=∠BAC+∠CAF=90°;
∵∠DCF=90°,∠DCE=45°,
∴∠FCE=90°﹣45°=45°,
∴∠DCE=∠FCE,
在△DCE和△FCE中,,
∴△DCE≌△FCE(SAS),
∴DE=EF,
在Rt△AEF中,AE2+AF2=EF2,
又∵AF=DB,
∴AE2+DB2=DE2.
25.(1) C(-6,-2);(2)不发生变化,值为;(3)EN=(EM-ON),证明见详解.
【详解】(1)如图(1)作CQ⊥OA于Q,
∴∠AQC=90°,
∵为等腰直角三角形,
∴AC=AB,∠CAB=90°,
∴∠QAC+∠OAB=90°,
∵∠QAC+∠ACQ=90°,
∴∠ACQ=∠BAO,
又∵AC=AB,∠AQC=∠AOB,
∴(AAS),
∴CQ=AO,AQ=BO,
∵OA=2,OB=4,
∴CQ=2,AQ=4,
∴OQ=6,
∴C(-6,-2).
(2)如图(2)作DP⊥OB于点P,
∴∠BPD=90°,
∵是等腰直角三角形,
∴AB=BD,∠ABD=∠ABO+∠OBD=90°,
∵∠OBD+∠BDP=90°,
∴∠ABO=∠BDP,
又∵AB=BD,∠AOB=∠BPD=90°,
∴
∴AO=BP,
∵BP=OB-PO=m-(-n)=m+n,
∵A,
∴OA=,
∴m+n=,
∴当点B沿y轴负半轴向下运动时,AO=BP=m+n=,
∴整式的值不变为.
(3)
证明:如图(3)所示,在ME上取一点G使得MG=ON,连接BG并延长,交x轴于H.
∵为等边三角形,
∴BO=BM=MO,∠OBM=∠OMB=∠BOM=60°,
∴EO=MO,∠EBM=105°,∠1=30°,
∵OE=OB,
∴OE=OM=BM,
∴∠3=∠EMO=15°,
∴∠BEM=30°,∠BME=45°,
∵OF⊥EB,
∴∠EOF=∠BME,
∴,
∴BG=EN,
∵ON=MG,
∴∠2=∠3,
∴∠2=15°,
∴∠EBG=90°,
∴BG=EG,
∴EN=EG,
∵EG=EM-GM,
∴EN=(EM-GM),
∴EN=(EM-ON).
答案第1页,共2页
答案 第1页,共6页 答案 第1页,共6页
