福建省福州市六校2023-2024学年高一下学期期末联考试题数学试题(PDF版,含答案)
文档属性
| 名称 | 福建省福州市六校2023-2024学年高一下学期期末联考试题数学试题(PDF版,含答案) |  | |
| 格式 | |||
| 文件大小 | 467.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-27 13:33:49 | ||
图片预览


文档简介
福州市六校 2023-2024学年高一下学期期末联考
数学试卷
(满分:150分,完卷时间:120分钟)
命题学校:
第一部分(选择题共 58分)
一 单选题:本大题共 8小题,每小题 5 分,共 40分,在每小题给出的四个选项中,只有一
项是符合题目要求的.
1. 复数 z (2 3i)(1 i)在复平面内对应的点位于( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
1 1
2. 甲 乙两人独立地破译一份密码,已知各人能破译的概率分别为 , ,则甲 乙两人一起破译这份密码,
4 5
密码被成功破译的概率为( )
1 7 2 9
A. B. C. D.
20 20 5 20
π
3. 已知平面向量 a,b 的夹角为 ,且 a 2,b ( 1, 3),则 a在b 方向上的投影向量为( )6
3 1 , 3 1
, 3 3
3 3
A. B.2 2 2 2
C. , 2 2
D.
,
2 2
4. 已知三条不重合的直线 a,b,c和平面 ,下列命题中是真命题的为( )
A. 若直线 a,b和平面 所成的角相等,则 a b
B. 若 a c,b c,则 a b
C. 若a ,a b,则b
D. 若 a ,b ,则 a b
5. 进入 8月份后,我市持续高温,气象局一般会提前发布高温橙色预警信号(高温橙色预警标准为 24小时
3
内最高气温将升至 37摄氏度以上),在今后的3天中,每一天最高气温在 37摄氏度以上的概率是 .用计算
5
机生成了 20组随机数,结果如下:
116 785 812 730 134 452 125 689 024 169
334 217 109 361 908 284 044 147 318 027
若用 0,1,2,3,4,5 表示高温橙色预警,用 6,7,8,9 表示非高温橙色预警,则今后的3 天中恰有 2
天发布高温橙色预警信号的概率估计是( )
3 13 2
A. B. 1
5 2
C. D.
20 5
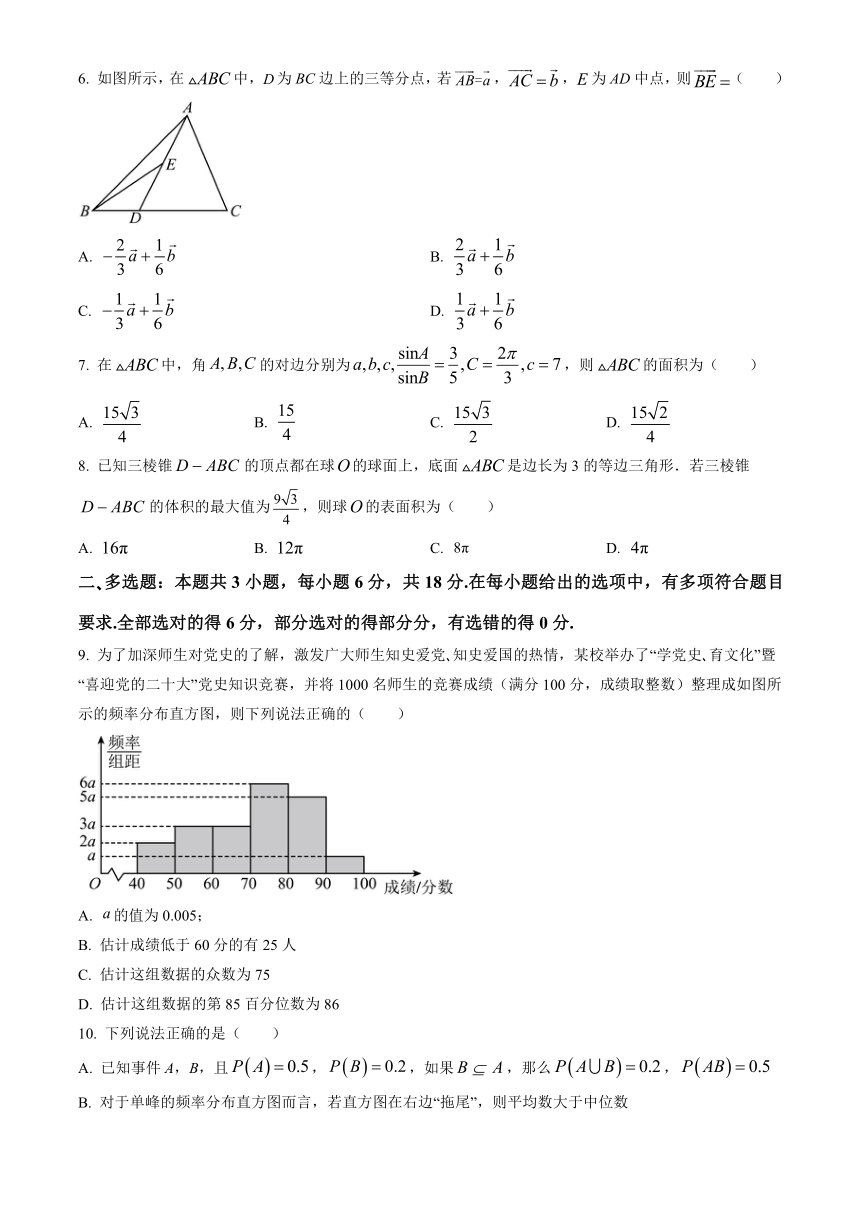
6. 如图所示,在 ABC中,D为 BC边上的三等分点,若 AB=a,AC b,E为 AD中点,则BE ( )
2 a 1
b 2 1
A. B. a b
3 6 3 6
1 a 1 1 1
C. b D. a b
3 6 3 6
sinA 3 2
7. 在 ABC中,角 A,B,C的对边分别为a,b,c, ,C ,c 7,则 ABC的面积为( )
sinB 5 3
15
A. 15 3 B. C. 15 3 D. 15 2
4 4 2 4
8. 已知三棱锥D ABC 的顶点都在球O的球面上,底面 ABC是边长为 3的等边三角形.若三棱锥
D ABC 9 3的体积的最大值为 ,则球O的表面积为( )
4
A. 16π B. 12π C. 8π D. 4π
二 多选题:本题共 3小题,每小题 6分,共 18分.在每小题给出的选项中,有多项符合题目
要求.全部选对的得 6分,部分选对的得部分分,有选错的得 0分.
9. 为了加深师生对党史的了解,激发广大师生知史爱党 知史爱国的热情,某校举办了“学党史 育文化”暨
“喜迎党的二十大”党史知识竞赛,并将 1000名师生的竞赛成绩(满分 100分,成绩取整数)整理成如图所
示的频率分布直方图,则下列说法正确的( )
A. a的值为 0.005;
B. 估计成绩低于 60分的有 25人
C. 估计这组数据的众数为 75
D. 估计这组数据的第 85百分位数为 86
10. 下列说法正确的是( )
A. 已知事件 A,B,且 P A 0.5, P B 0.2,如果 B A,那么 P A B 0.2,P AB 0.5
B. 对于单峰的频率分布直方图而言,若直方图在右边“拖尾”,则平均数大于中位数
C. 若 A,B是两个互斥事件,则 P A B 1
D. 若事件 A,B,C两两独立,则 P ABC P A P B P C
11. 如图,棱长为1的正方体中 ABCD A1B1C1D1中,下列结论正确的是( )
A. 异面直线 B1D1与 BC1所成的角为60
B. 直线 A 1C与平面C1CDD1所成的角为 45
C. 二面角B C1D D1平面角的正切值为 2
D. A BDC 2 3点 1到平面 1的距离为
3
第二部分(非选择题共 92分)
三 填空题:本题共 3小题,每小题 5分,共 15分.
12. 在正四棱锥P ABCD中, PA AB 2,则该棱锥的体积为____________.
13. 在对某中学高一年级学生身高(单位: cm)调查中,抽取了男生 20 人,其平均数和方差分别为 174
和 12,抽取了女生 30 人,其平均数和方差分别为 164 和 30,根据这些数据计算出总样本的平均数为
__________,方差为__________.
14. 设样本空间 1,2,3,4,5,6,7,8 含有等可能的样本点,且事件 A 1,2,3,4 ,事件 B 1,2,3,5 ,
事件C 1,m,n,8 ,使得 P ABC P A P B P C ,且满足 A,B,C两两不独立,则m n ______.
四 解答题:本题共 5小题,共 77分.解答应写出文字说明 证明过程或演算步骤.
15. 已知复数 z m 2i是方程 x2 6x 13 0的一个虚根( i是虚数单位, m R ).
(1)求 | z |;
z
(2)复数 z1 a i,若 z 为纯虚数,求实数
a的值.
1
16. 已知向量 a,b满足 a 3, b 2, a 2b 31.
(1)求向量 a,b的夹角 的大小;
(2)设向量m 3a b ,n a kb ,若m,n的夹角为锐角,求实数 k的取值范围.
17. 新课标设置后,特别强调了要增加对数学文化的考查,某市高二年级期末考试特命制了一套与数学文化
有关的期末模拟试卷,试卷满分 150分,并对整个高二年级的学生进行了测试.现从这些学生中随机抽取
了 100名学生的成绩,按照成绩为 90,100 , 100,110 ,…, 140,150 分成了 6组,制成了如图所示的
频率分布直方图(假定每名学生的成绩均不低于 90分).
(1)求频率分布直方图中的 x的值,并估计所抽取的 100名学生成绩的平均分(同一组中的数据用该组区
间的中点值代表);
(2)若利用分层抽样的方法从样本中成绩位于 120,140 的两组学生中抽取 6人,再从这 6人中随机抽取
2人参加这次考试的考情分析会,试求 130,140 这组中至少有 1人被抽到的概率.
18. 已知 AB 平面 ACD,DE 平面 ACD, ACD为等边三角形,AD DE 2,AB 1,F 为CD
的中点.
(1)求证: AF //平面 BCE;
(2)求证:平面BCE 平面CDE;
(3)求直线 BF 和平面BCE所成角的正弦值.
19. 如图,设 ABC 中角 A,B,C 所对的边分别为 a,b,c, AD 为 BC 边上的中线,已知 c 1,且
2csinAcosB asinA 15csinC, cos 21 BAD .
7
(1)求b的值;
(2)求 ABC的面积;
(3)设点 E,F 分别为边 AB, AC上的动点(含端点),线段 EF 交 AD于G,且△AEF 的面积为 ABC面
1
积的 ,求 的取值范围.
6 AG EF
参考答案
1. D
2. C.
3. D
4. D
5. B
6. A
7. A.
8. A.
9. ACD
10. BC
11. ACD.
12. 4 2 .
3
13. 168;46.8 .
14. 13
15. (1) 13
2
(2)
3
π
16. (1)
6
6 1 1
(2) , 5 3
, 3
17. (1) x 0.02,平均分为116.5;
3
(2)
5
18.(1)证明:取CE的中点G,连接 FG 、BG.
GF 1 F 为CD的中点, GF //DE且 DE.
2
Q AB 平面 ACD,DE 平面 ACD,
AB//DE, GF //AB.
AB 1又 DE, GF AB.
2
四边形GFAB为平行四边形,则 AF //BG.
AF 平面 BCE, BG 平面 BCE,
AF //平面 BCE.
(2)证明: ACD为等边三角形, F 为CD的中点, AF CD.
DE 平面 ACD, AF 平面 ACD, DE AF .
BG //AF ,所以DE BG, BG CD,
又CD DE D,CD,DE 平面CDE,
BG 平面CDE.
BG 平面 BCE, 平面 BCE 平面CDE.
2
(3)
4
19. (1)b 4
(2) 3
(3) 0,
5
2
数学试卷
(满分:150分,完卷时间:120分钟)
命题学校:
第一部分(选择题共 58分)
一 单选题:本大题共 8小题,每小题 5 分,共 40分,在每小题给出的四个选项中,只有一
项是符合题目要求的.
1. 复数 z (2 3i)(1 i)在复平面内对应的点位于( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
1 1
2. 甲 乙两人独立地破译一份密码,已知各人能破译的概率分别为 , ,则甲 乙两人一起破译这份密码,
4 5
密码被成功破译的概率为( )
1 7 2 9
A. B. C. D.
20 20 5 20
π
3. 已知平面向量 a,b 的夹角为 ,且 a 2,b ( 1, 3),则 a在b 方向上的投影向量为( )6
3 1 , 3 1
, 3 3
3 3
A. B.2 2 2 2
C. , 2 2
D.
,
2 2
4. 已知三条不重合的直线 a,b,c和平面 ,下列命题中是真命题的为( )
A. 若直线 a,b和平面 所成的角相等,则 a b
B. 若 a c,b c,则 a b
C. 若a ,a b,则b
D. 若 a ,b ,则 a b
5. 进入 8月份后,我市持续高温,气象局一般会提前发布高温橙色预警信号(高温橙色预警标准为 24小时
3
内最高气温将升至 37摄氏度以上),在今后的3天中,每一天最高气温在 37摄氏度以上的概率是 .用计算
5
机生成了 20组随机数,结果如下:
116 785 812 730 134 452 125 689 024 169
334 217 109 361 908 284 044 147 318 027
若用 0,1,2,3,4,5 表示高温橙色预警,用 6,7,8,9 表示非高温橙色预警,则今后的3 天中恰有 2
天发布高温橙色预警信号的概率估计是( )
3 13 2
A. B. 1
5 2
C. D.
20 5
6. 如图所示,在 ABC中,D为 BC边上的三等分点,若 AB=a,AC b,E为 AD中点,则BE ( )
2 a 1
b 2 1
A. B. a b
3 6 3 6
1 a 1 1 1
C. b D. a b
3 6 3 6
sinA 3 2
7. 在 ABC中,角 A,B,C的对边分别为a,b,c, ,C ,c 7,则 ABC的面积为( )
sinB 5 3
15
A. 15 3 B. C. 15 3 D. 15 2
4 4 2 4
8. 已知三棱锥D ABC 的顶点都在球O的球面上,底面 ABC是边长为 3的等边三角形.若三棱锥
D ABC 9 3的体积的最大值为 ,则球O的表面积为( )
4
A. 16π B. 12π C. 8π D. 4π
二 多选题:本题共 3小题,每小题 6分,共 18分.在每小题给出的选项中,有多项符合题目
要求.全部选对的得 6分,部分选对的得部分分,有选错的得 0分.
9. 为了加深师生对党史的了解,激发广大师生知史爱党 知史爱国的热情,某校举办了“学党史 育文化”暨
“喜迎党的二十大”党史知识竞赛,并将 1000名师生的竞赛成绩(满分 100分,成绩取整数)整理成如图所
示的频率分布直方图,则下列说法正确的( )
A. a的值为 0.005;
B. 估计成绩低于 60分的有 25人
C. 估计这组数据的众数为 75
D. 估计这组数据的第 85百分位数为 86
10. 下列说法正确的是( )
A. 已知事件 A,B,且 P A 0.5, P B 0.2,如果 B A,那么 P A B 0.2,P AB 0.5
B. 对于单峰的频率分布直方图而言,若直方图在右边“拖尾”,则平均数大于中位数
C. 若 A,B是两个互斥事件,则 P A B 1
D. 若事件 A,B,C两两独立,则 P ABC P A P B P C
11. 如图,棱长为1的正方体中 ABCD A1B1C1D1中,下列结论正确的是( )
A. 异面直线 B1D1与 BC1所成的角为60
B. 直线 A 1C与平面C1CDD1所成的角为 45
C. 二面角B C1D D1平面角的正切值为 2
D. A BDC 2 3点 1到平面 1的距离为
3
第二部分(非选择题共 92分)
三 填空题:本题共 3小题,每小题 5分,共 15分.
12. 在正四棱锥P ABCD中, PA AB 2,则该棱锥的体积为____________.
13. 在对某中学高一年级学生身高(单位: cm)调查中,抽取了男生 20 人,其平均数和方差分别为 174
和 12,抽取了女生 30 人,其平均数和方差分别为 164 和 30,根据这些数据计算出总样本的平均数为
__________,方差为__________.
14. 设样本空间 1,2,3,4,5,6,7,8 含有等可能的样本点,且事件 A 1,2,3,4 ,事件 B 1,2,3,5 ,
事件C 1,m,n,8 ,使得 P ABC P A P B P C ,且满足 A,B,C两两不独立,则m n ______.
四 解答题:本题共 5小题,共 77分.解答应写出文字说明 证明过程或演算步骤.
15. 已知复数 z m 2i是方程 x2 6x 13 0的一个虚根( i是虚数单位, m R ).
(1)求 | z |;
z
(2)复数 z1 a i,若 z 为纯虚数,求实数
a的值.
1
16. 已知向量 a,b满足 a 3, b 2, a 2b 31.
(1)求向量 a,b的夹角 的大小;
(2)设向量m 3a b ,n a kb ,若m,n的夹角为锐角,求实数 k的取值范围.
17. 新课标设置后,特别强调了要增加对数学文化的考查,某市高二年级期末考试特命制了一套与数学文化
有关的期末模拟试卷,试卷满分 150分,并对整个高二年级的学生进行了测试.现从这些学生中随机抽取
了 100名学生的成绩,按照成绩为 90,100 , 100,110 ,…, 140,150 分成了 6组,制成了如图所示的
频率分布直方图(假定每名学生的成绩均不低于 90分).
(1)求频率分布直方图中的 x的值,并估计所抽取的 100名学生成绩的平均分(同一组中的数据用该组区
间的中点值代表);
(2)若利用分层抽样的方法从样本中成绩位于 120,140 的两组学生中抽取 6人,再从这 6人中随机抽取
2人参加这次考试的考情分析会,试求 130,140 这组中至少有 1人被抽到的概率.
18. 已知 AB 平面 ACD,DE 平面 ACD, ACD为等边三角形,AD DE 2,AB 1,F 为CD
的中点.
(1)求证: AF //平面 BCE;
(2)求证:平面BCE 平面CDE;
(3)求直线 BF 和平面BCE所成角的正弦值.
19. 如图,设 ABC 中角 A,B,C 所对的边分别为 a,b,c, AD 为 BC 边上的中线,已知 c 1,且
2csinAcosB asinA 15csinC, cos 21 BAD .
7
(1)求b的值;
(2)求 ABC的面积;
(3)设点 E,F 分别为边 AB, AC上的动点(含端点),线段 EF 交 AD于G,且△AEF 的面积为 ABC面
1
积的 ,求 的取值范围.
6 AG EF
参考答案
1. D
2. C.
3. D
4. D
5. B
6. A
7. A.
8. A.
9. ACD
10. BC
11. ACD.
12. 4 2 .
3
13. 168;46.8 .
14. 13
15. (1) 13
2
(2)
3
π
16. (1)
6
6 1 1
(2) , 5 3
, 3
17. (1) x 0.02,平均分为116.5;
3
(2)
5
18.(1)证明:取CE的中点G,连接 FG 、BG.
GF 1 F 为CD的中点, GF //DE且 DE.
2
Q AB 平面 ACD,DE 平面 ACD,
AB//DE, GF //AB.
AB 1又 DE, GF AB.
2
四边形GFAB为平行四边形,则 AF //BG.
AF 平面 BCE, BG 平面 BCE,
AF //平面 BCE.
(2)证明: ACD为等边三角形, F 为CD的中点, AF CD.
DE 平面 ACD, AF 平面 ACD, DE AF .
BG //AF ,所以DE BG, BG CD,
又CD DE D,CD,DE 平面CDE,
BG 平面CDE.
BG 平面 BCE, 平面 BCE 平面CDE.
2
(3)
4
19. (1)b 4
(2) 3
(3) 0,
5
2
同课章节目录
