北师大版八年级下册6.2.1平行四边形的判定 课件(共14张PPT)
文档属性
| 名称 | 北师大版八年级下册6.2.1平行四边形的判定 课件(共14张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 374.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-27 00:00:00 | ||
图片预览


文档简介
(共14张PPT)
6.2 平行四边形的判定
第六章 平行四边形
情境引入
学习目标
1、探究并掌握从边、角和对角线的角度判定平行四边形的判定定理 (重点)
2、会运用平行四边形的判定定理进行推理证明(难点)
平行四边形的判定
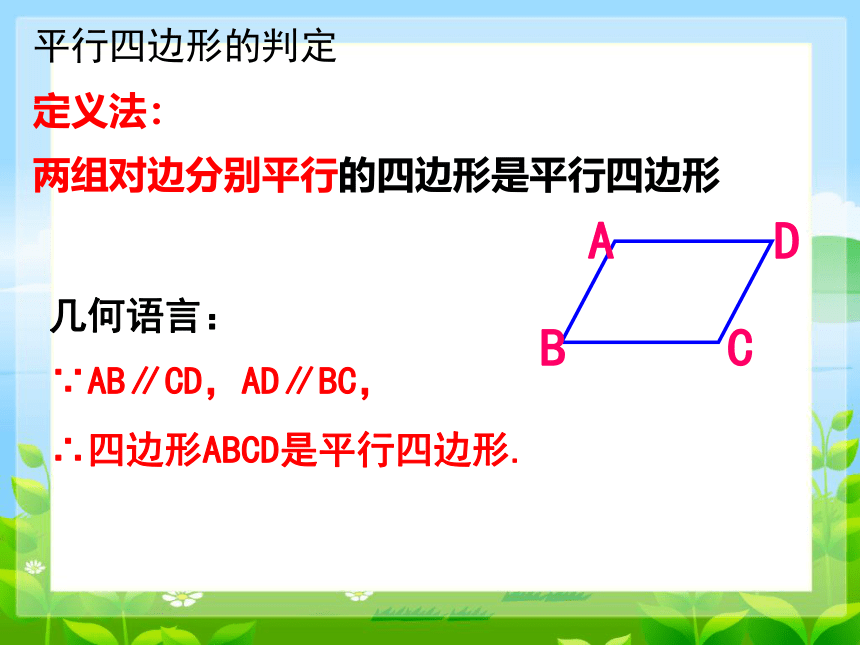
定义法:
两组对边分别平行的四边形是平行四边形
A
B
C
D
几何语言:
∵AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形.
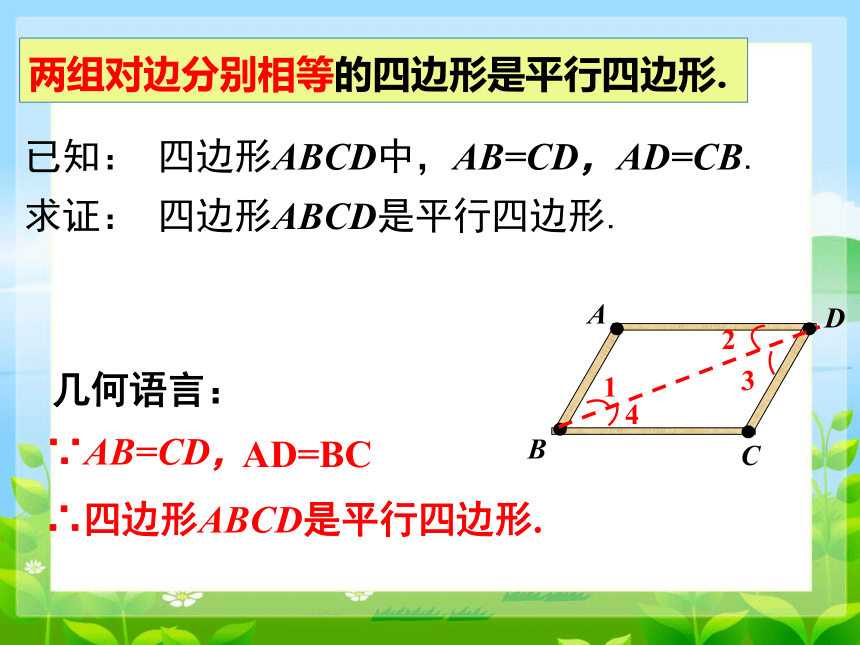
已知: 四边形ABCD中,AB=CD,AD=CB.
求证: 四边形ABCD是平行四边形.
A
B
C
D
1
4
2
3
两组对边分别相等的四边形是平行四边形.
∵AB=CD,
∴四边形ABCD是平行四边形.
几何语言:
AD=BC
D
A
B
C
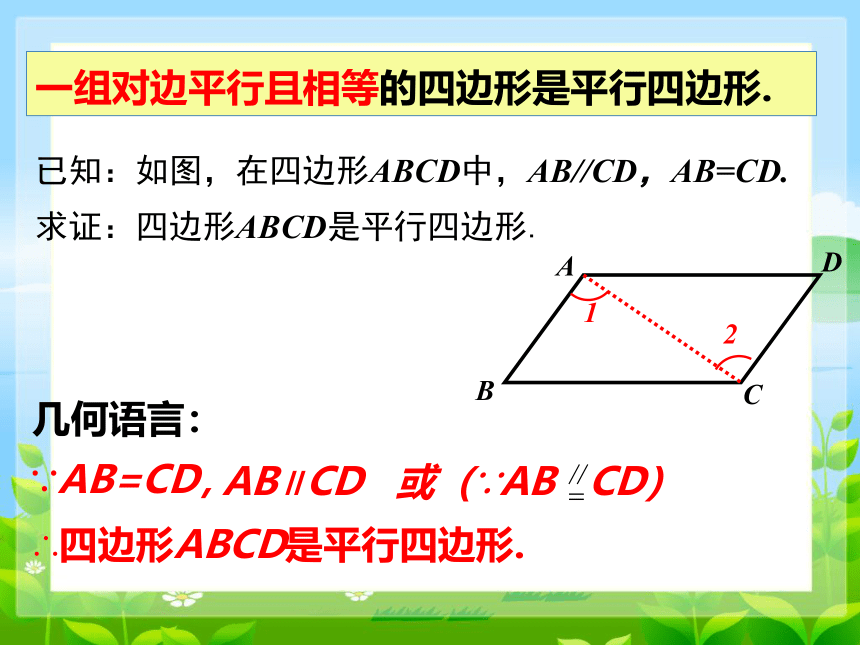
已知:如图,在四边形ABCD中,AB//CD,AB=CD.
求证:四边形ABCD是平行四边形.
1
2
一组对边平行且相等的四边形是平行四边形.
∵AB=CD,
AB∥CD 或(∵AB CD)
∴四边形ABCD是平行四边形.
几何语言:
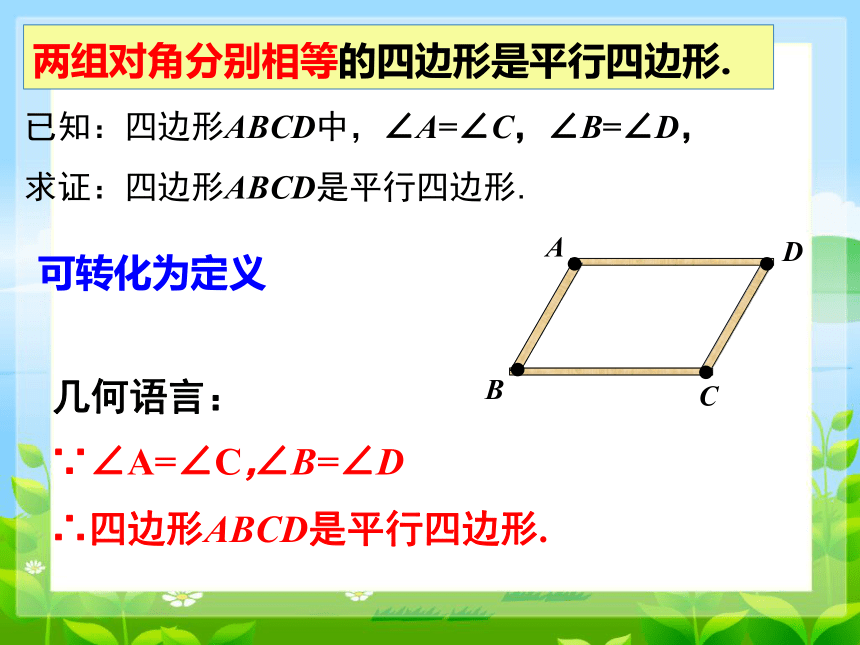
已知:四边形ABCD中,∠A=∠C,∠B=∠D,
求证:四边形ABCD是平行四边形.
A
B
C
D
两组对角分别相等的四边形是平行四边形.
∵∠A=∠C,
∠B=∠D
∴四边形ABCD是平行四边形.
几何语言:
可转化为定义
A
B
C
D
O
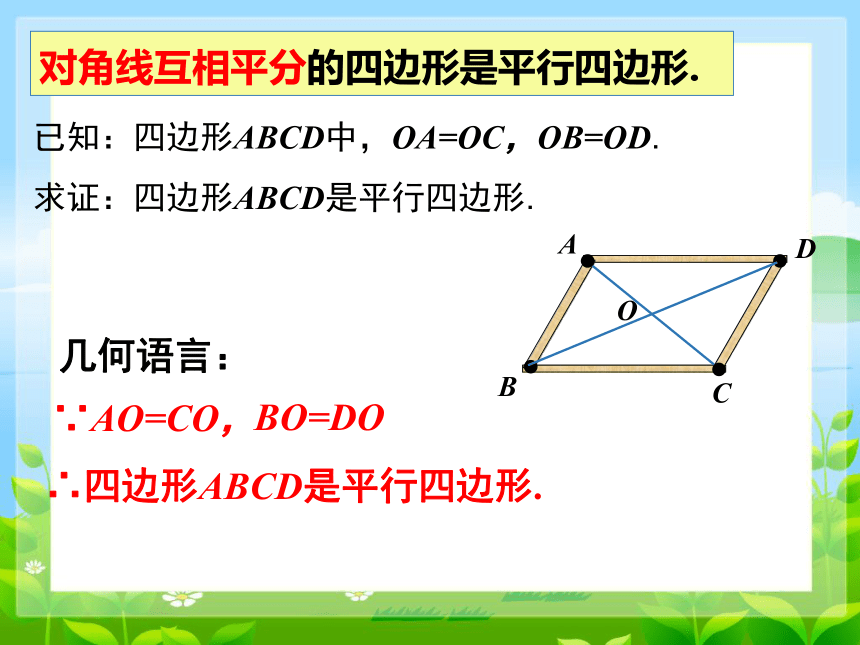
已知:四边形ABCD中,OA=OC,OB=OD.
求证:四边形ABCD是平行四边形.
对角线互相平分的四边形是平行四边形.
∵AO=CO,
∴四边形ABCD是平行四边形.
几何语言:
BO=DO
从边考虑
两组对边分别平行的四边形是平行四边形(定义法)
两组对边分别相等的四边形是平行四边形(判定定理1)
一组对边平行且相等的四边形是平行四边形(判定定理2)
从角考虑
从对角线考虑
平行四边形的判定方法
两组对角分别相等的四边形是平行四边形(可转化为定义法)
对角线互相平分的四边形是平行四边形(判定定理3)
课堂小结
1.如图,E、F分别在于 ABCD两边AB、DC上,
且AE=DF。
求证:(1)四边形AEFD是平行四边形。
(2)四边形BEFC是平行四边形。
实践应用
一组对边平行且相等
的四边形是平行四边形.
2. 如图,在 ABCD中,E,F,G,H分别是
AB,BC,CD,AD的中点,
求证:四边形EFGH是平行四边形。
实践应用
两组对边分别相等
的四边形是平行四边形.
3. 如图在 ABCD中,E、F分别是 AD、BC的中点,
求证:四边形BEDF是平行四边形。
实践应用
一组对边平行且相等
的四边形是平行四边形.
4. 如图在 ABCD中,E、F分别是 AD、BC的中点,
求证:四边形MENF是平行四边形。
实践应用
两组对边分别平行
的四边形是平行四边形.
5. 如图在 ABCD中,BE,DF分别是∠ABC, ∠ADC
的角平分线于AD,BC的交点,
求证:四边形BEDF是平行四边形。
实践应用
两组对边分别平行
的四边形是平行四边形.
D
A
B
C
E
F
6、已知:E、F是平行四边形ABCD对角线
AC上的两点,并且AE=CF。
求证:四边形BFDE是平行四边形
实践应用
对角线互相平分
的四边形是平行四边形.
6.2 平行四边形的判定
第六章 平行四边形
情境引入
学习目标
1、探究并掌握从边、角和对角线的角度判定平行四边形的判定定理 (重点)
2、会运用平行四边形的判定定理进行推理证明(难点)
平行四边形的判定
定义法:
两组对边分别平行的四边形是平行四边形
A
B
C
D
几何语言:
∵AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形.
已知: 四边形ABCD中,AB=CD,AD=CB.
求证: 四边形ABCD是平行四边形.
A
B
C
D
1
4
2
3
两组对边分别相等的四边形是平行四边形.
∵AB=CD,
∴四边形ABCD是平行四边形.
几何语言:
AD=BC
D
A
B
C
已知:如图,在四边形ABCD中,AB//CD,AB=CD.
求证:四边形ABCD是平行四边形.
1
2
一组对边平行且相等的四边形是平行四边形.
∵AB=CD,
AB∥CD 或(∵AB CD)
∴四边形ABCD是平行四边形.
几何语言:
已知:四边形ABCD中,∠A=∠C,∠B=∠D,
求证:四边形ABCD是平行四边形.
A
B
C
D
两组对角分别相等的四边形是平行四边形.
∵∠A=∠C,
∠B=∠D
∴四边形ABCD是平行四边形.
几何语言:
可转化为定义
A
B
C
D
O
已知:四边形ABCD中,OA=OC,OB=OD.
求证:四边形ABCD是平行四边形.
对角线互相平分的四边形是平行四边形.
∵AO=CO,
∴四边形ABCD是平行四边形.
几何语言:
BO=DO
从边考虑
两组对边分别平行的四边形是平行四边形(定义法)
两组对边分别相等的四边形是平行四边形(判定定理1)
一组对边平行且相等的四边形是平行四边形(判定定理2)
从角考虑
从对角线考虑
平行四边形的判定方法
两组对角分别相等的四边形是平行四边形(可转化为定义法)
对角线互相平分的四边形是平行四边形(判定定理3)
课堂小结
1.如图,E、F分别在于 ABCD两边AB、DC上,
且AE=DF。
求证:(1)四边形AEFD是平行四边形。
(2)四边形BEFC是平行四边形。
实践应用
一组对边平行且相等
的四边形是平行四边形.
2. 如图,在 ABCD中,E,F,G,H分别是
AB,BC,CD,AD的中点,
求证:四边形EFGH是平行四边形。
实践应用
两组对边分别相等
的四边形是平行四边形.
3. 如图在 ABCD中,E、F分别是 AD、BC的中点,
求证:四边形BEDF是平行四边形。
实践应用
一组对边平行且相等
的四边形是平行四边形.
4. 如图在 ABCD中,E、F分别是 AD、BC的中点,
求证:四边形MENF是平行四边形。
实践应用
两组对边分别平行
的四边形是平行四边形.
5. 如图在 ABCD中,BE,DF分别是∠ABC, ∠ADC
的角平分线于AD,BC的交点,
求证:四边形BEDF是平行四边形。
实践应用
两组对边分别平行
的四边形是平行四边形.
D
A
B
C
E
F
6、已知:E、F是平行四边形ABCD对角线
AC上的两点,并且AE=CF。
求证:四边形BFDE是平行四边形
实践应用
对角线互相平分
的四边形是平行四边形.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
