4.1 函数 课件(共26张PPT)北师大版数学八年级上册
文档属性
| 名称 | 4.1 函数 课件(共26张PPT)北师大版数学八年级上册 |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-27 00:00:00 | ||
图片预览




文档简介
(共26张PPT)
第四章《一次函数》
4.1 函数
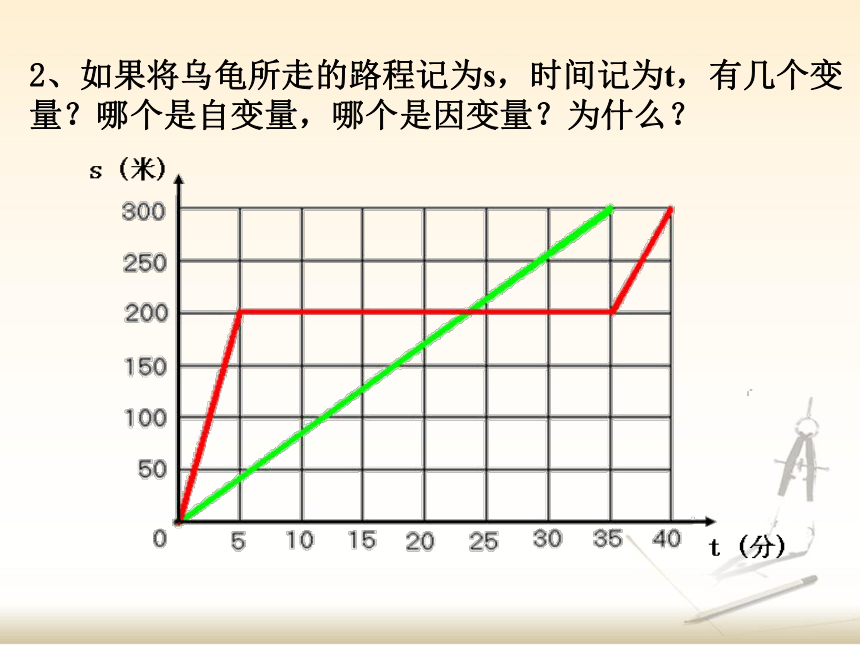
1、你能结合该图象中的数据讲述这个故事吗?
2、如果将乌龟所走的路程记为s,时间记为t,有几个变量?哪个是自变量,哪个是因变量?为什么?
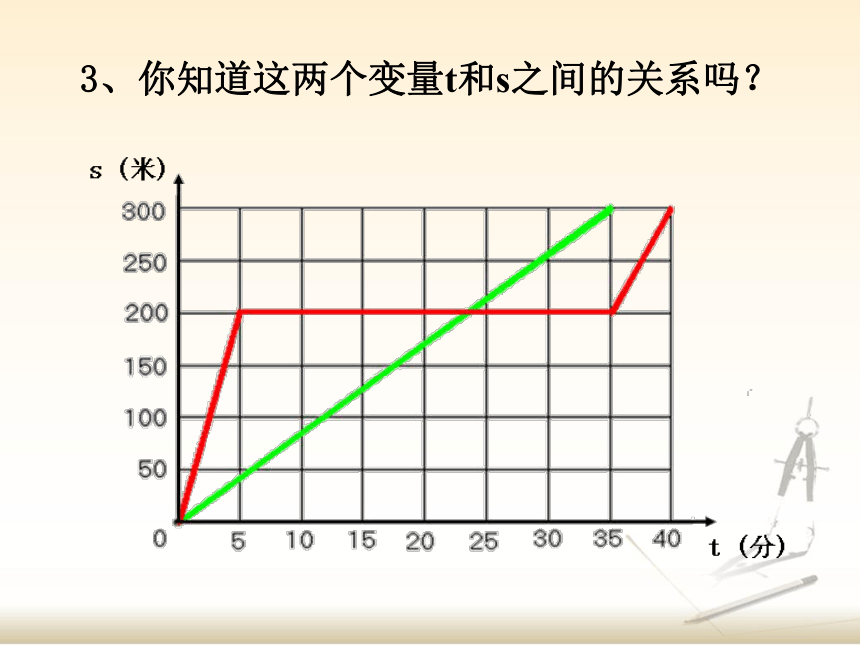
3、你知道这两个变量t和s之间的关系吗?
《义务教育课程标准实验教科书》北师大版
第四章 一次函数
4.1 函数
函数是刻画变量之间关系的常用模型,其中最为简单的是一次函数,什么是一次函数?它对应的图象有什么特征 用一次函数可以解决现实生活中的哪些问题?……你想了解吗?一起来看一看!
问题1:
你坐过摩天轮吗?
想一想,如果你坐在摩天轮上,随着时间的变化,你离开地面的高度是如何变化的?
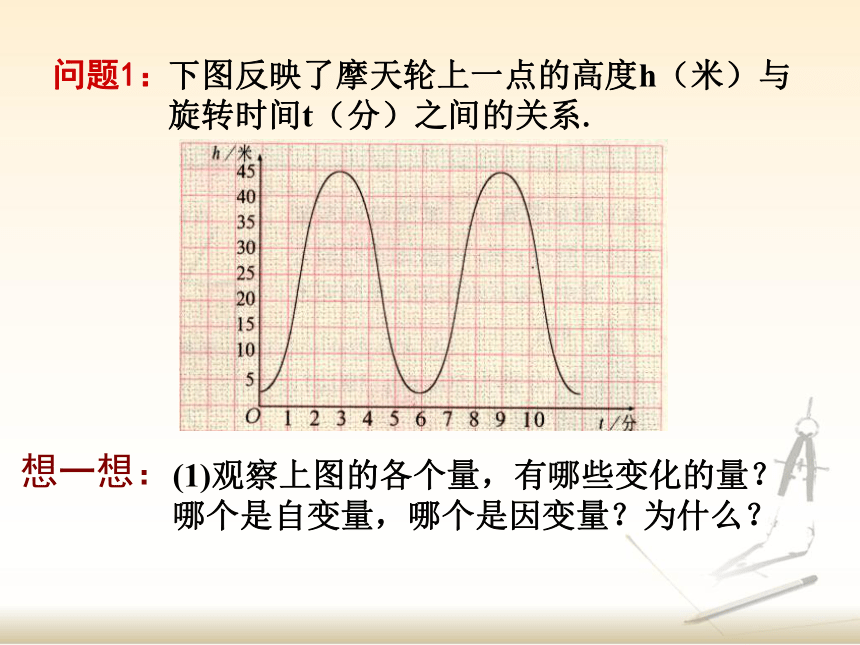
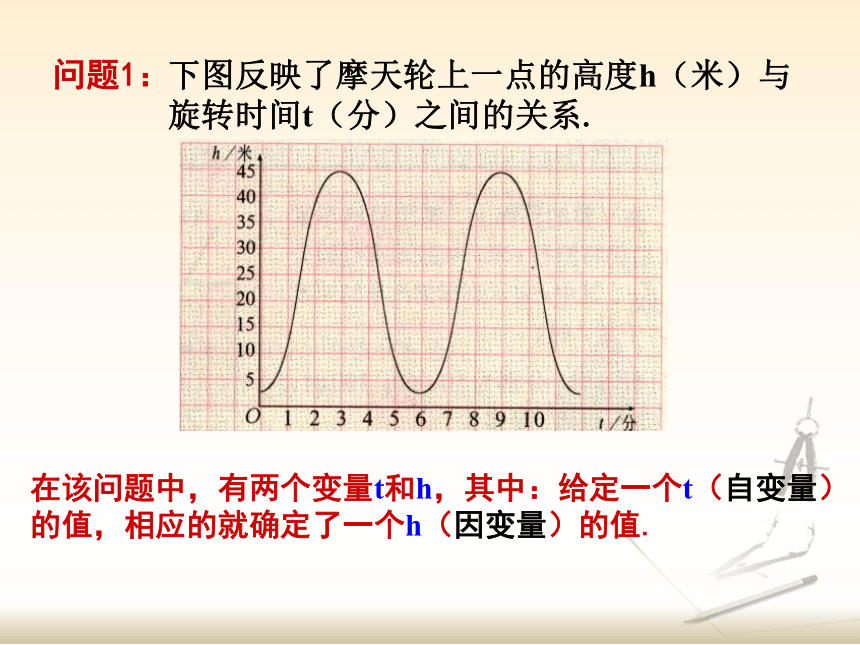
下图反映了摩天轮上一点的高度h(米)与旋转时间t(分)之间的关系.
问题1:
(1)观察上图的各个量,有哪些变化的量?
哪个是自变量,哪个是因变量?为什么?
想一想:
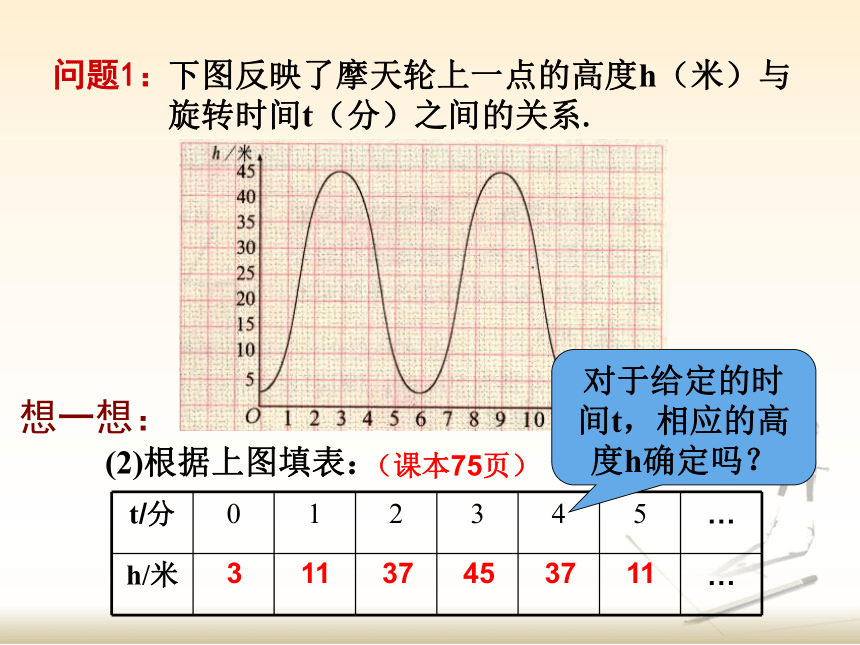
(2)根据上图填表:
t/分 0 1 2 3 4 5 …
h/米 …
(课本75页)
3
45
37
11
11
37
对于给定的时间t,相应的高度h确定吗?
想一想:
问题1:
下图反映了摩天轮上一点的高度h(米)与旋转时间t(分)之间的关系.
在该问题中,有两个变量t和h,其中:给定一个t(自变量)
的值,相应的就确定了一个h(因变量)的值.
问题1:
下图反映了摩天轮上一点的高度h(米)与旋转时间t(分)之间的关系.
瓶子和罐头盒等圆柱形的物体,常常如下图那样堆放.随着层数的增加,物体的总数是如何变化的?
层数n 1 2 3 4 5 ···
物体总数y ···
1
3
6
10
15
问题2:
根据上图,填写下表:
对于给定的层数n,相应的物体总数y确定吗?
瓶子和罐头盒等圆柱形的物体,常常如下图那样堆放.随着层数的增加,物体的总数是如何变化的?
层数n 1 2 3 4 5 ···
物体总数y ···
1
3
6
10
15
问题2:
在该问题中,有两个变量n和y,其中:给定一个n(自变量)
的值,相应的就确定了一个y(因变量)的值.
(3)给定一个v值,你都能求出 相应的s值吗?给定一个v值,你求出了几个s值?
问题3:
在平整的路面上,某型号汽车紧急刹车后仍将
滑行s米,一般地有经验公式 ,其中v表示刹车
前汽车的速度(单位:千米/时).
(1)公式中有几个变化的量?
哪个是自变量,哪个是因变量?
速度v
距离s
想一想:
(2)计算当v分别为50,60,100
时,相应的滑行距离s是多少?
速度v
距离s
在该问题中,有两个变量v和s,
其中:给定一个v(自变量)的值,相应的就确定了一个s(因变量)
的值.
问题3:
在平整的路面上,某型号汽车紧急刹车后仍将
滑行s米,一般地有经验公式 ,其中v表示刹车
前汽车的速度(单位:千米/时).
在上面的各个问题中,都有两个变量:① 旋转时间t和高度h;②层数n和物体总数y;③刹车前速度v和刹车距离s.如果给定其中一个变量(自变量)的值,相应地就确定了另一个变量(因变量)的值.
一般地,在某个变化过程中,有两个变量x和y,并且对于变量x的每一个值,变量y都有唯一确定的值与它对应,那么我们称y是x的函数,其中x是自变量,y是因变量.
以上三个问题,从变量的个数及变量之间的关系看,它们有什么共同点?
关键词:两个变量,一个x值对应唯一确定的一个y值.
层数n 1 2 3 4 5 ······
物体总数y ······
想一想:
1
3
6
10
15
数学世家的光荣——函数的出现
17世纪,在瑞士的巴塞尔有一个祖孙五代数学家,成员数十人的家族——贝努利家族,其中最著名的是雅各、约翰、丹尼尔.欧拉从12岁起,就是这个家族成员的好朋友.他和同龄人尼古拉、丹尼尔结识,成为终生盟友,这两位兄长给欧拉讲了许多有趣的数学故事,吸引了他那颗幼小好奇的心灵,使欧拉从小立志,将来能像贝努利家族成员一样,腾飞于数学长空.1720年,欧拉在约翰·贝努利教授的推荐下,13岁成为巴塞尔大学的学生,从此他在约翰·贝努利的指导下迅速成长着.欧拉成为了贝努利家庭的一个成员,被世人传为佳话.
函数是中学数学中最重要的概念之一,函数
概念产生于300年前.笛卡儿引入了坐标系,使数
学发生了巨大变革,但他没用变量这个词.在数学
上使用变量这个词最早的是欧拉的老师约翰·贝努
利,他给函数下了这样的定义:“所谓变量的函数,
就是变量与常量组成的表达式”.
1775年,欧拉在《微分学》中给出了我们教科书中的定义.
读一读:
层数n 1 2 3 4 5 ······
物体总数y ······
速度v
距离s
高度h是时间t的函数
距离s是速度v的函数
1
3
6
10
15
物体总数y是层数n的函数
·
—数
——形
以上三个函数的表示方式有什么不同?
层数n 1 2 3 4 5 ······
物体总数y ······
想一想:
1
3
6
10
15
想一想:
不同点:在第一个问题中,是以图象的形式表示两个变量之间的关系,第二个问题中是列表的形式以表示两个变量之间的关系,第三个问题是以关系式的形式表示两个变量之间的关系.
函数常用的三种表示方式:
(1)图象法;(2)列表法;(3)关系式法.
以上三个函数的表示方式有什么不同?
以上三个问题中,自变量能取哪些值?
层数n 1 2 3 4 5 ······
物体总数y ······
想一想:
1
3
6
10
15
在龟兔赛跑问题中,如果将乌龟、兔子所走的路程分别记为s1和 s2,则 s1能看成是时间t的函数吗?为什么?s2能看成t的函数吗?
乌龟
兔子
( s1 )
( s2 )
问题解决:
·
·
·
思考生活中的某个变化过程,看看其中
是否存在函数关系,并指出自变量的取值范围.
具体要求:
四人为一小组,交流各自的想法;由一人负责整理大家的想法并向全班同学展示,其它同学可以补充.
联系生活:
1、下列各题中分别有几个变量?你能将其中某个变量看成另一个变量的函数吗?若能,请指出自变量的取值范围.
随堂练习:
2、已知菱形ABCD的对角线AC长为4,BD的长x在变化,则菱形的面积为y=-×4×x.本题中有几个变量?你能将其中某个变量看成另一个变量的函数吗?若能,请指出自变量的取值范围.
1
2
随堂练习:
3、在国内投寄60g以内的平信应付邮资如下表:
信件质量m/克
邮资y/元 1.20 2.40 3.60
上表中有几个变量?你能将其中某个变量看成另一个变量的函数吗?若能,请指出自变量的取值范围.
随堂练习:
通过这节课的学习,你有什么收获?
课堂小结:
1.知识内容:
2.学习流程:
3.思想与方法:
(1)函数的定义: 一般地,在某个变化过程中,有两个变量x和y,如果对于变量x的每一个值,变量y都有唯一的值与它对应,那么我们称y是x的函数,其中x是自变量,y是因变量.
(2)函数的三种表示方式:图象法;列表法;关系式法.
三个实际
问题讨论
总结共性
定义函数
问题解决
深入理解
联系生活
体会应用
数形结合思想;用函数的观点认识现实世界.
课后作业:
1.P77,知识技能1;
2.课下利用网络、书籍搜集关于函数的有关资料,在班内交流分享.
第四章《一次函数》
4.1 函数
1、你能结合该图象中的数据讲述这个故事吗?
2、如果将乌龟所走的路程记为s,时间记为t,有几个变量?哪个是自变量,哪个是因变量?为什么?
3、你知道这两个变量t和s之间的关系吗?
《义务教育课程标准实验教科书》北师大版
第四章 一次函数
4.1 函数
函数是刻画变量之间关系的常用模型,其中最为简单的是一次函数,什么是一次函数?它对应的图象有什么特征 用一次函数可以解决现实生活中的哪些问题?……你想了解吗?一起来看一看!
问题1:
你坐过摩天轮吗?
想一想,如果你坐在摩天轮上,随着时间的变化,你离开地面的高度是如何变化的?
下图反映了摩天轮上一点的高度h(米)与旋转时间t(分)之间的关系.
问题1:
(1)观察上图的各个量,有哪些变化的量?
哪个是自变量,哪个是因变量?为什么?
想一想:
(2)根据上图填表:
t/分 0 1 2 3 4 5 …
h/米 …
(课本75页)
3
45
37
11
11
37
对于给定的时间t,相应的高度h确定吗?
想一想:
问题1:
下图反映了摩天轮上一点的高度h(米)与旋转时间t(分)之间的关系.
在该问题中,有两个变量t和h,其中:给定一个t(自变量)
的值,相应的就确定了一个h(因变量)的值.
问题1:
下图反映了摩天轮上一点的高度h(米)与旋转时间t(分)之间的关系.
瓶子和罐头盒等圆柱形的物体,常常如下图那样堆放.随着层数的增加,物体的总数是如何变化的?
层数n 1 2 3 4 5 ···
物体总数y ···
1
3
6
10
15
问题2:
根据上图,填写下表:
对于给定的层数n,相应的物体总数y确定吗?
瓶子和罐头盒等圆柱形的物体,常常如下图那样堆放.随着层数的增加,物体的总数是如何变化的?
层数n 1 2 3 4 5 ···
物体总数y ···
1
3
6
10
15
问题2:
在该问题中,有两个变量n和y,其中:给定一个n(自变量)
的值,相应的就确定了一个y(因变量)的值.
(3)给定一个v值,你都能求出 相应的s值吗?给定一个v值,你求出了几个s值?
问题3:
在平整的路面上,某型号汽车紧急刹车后仍将
滑行s米,一般地有经验公式 ,其中v表示刹车
前汽车的速度(单位:千米/时).
(1)公式中有几个变化的量?
哪个是自变量,哪个是因变量?
速度v
距离s
想一想:
(2)计算当v分别为50,60,100
时,相应的滑行距离s是多少?
速度v
距离s
在该问题中,有两个变量v和s,
其中:给定一个v(自变量)的值,相应的就确定了一个s(因变量)
的值.
问题3:
在平整的路面上,某型号汽车紧急刹车后仍将
滑行s米,一般地有经验公式 ,其中v表示刹车
前汽车的速度(单位:千米/时).
在上面的各个问题中,都有两个变量:① 旋转时间t和高度h;②层数n和物体总数y;③刹车前速度v和刹车距离s.如果给定其中一个变量(自变量)的值,相应地就确定了另一个变量(因变量)的值.
一般地,在某个变化过程中,有两个变量x和y,并且对于变量x的每一个值,变量y都有唯一确定的值与它对应,那么我们称y是x的函数,其中x是自变量,y是因变量.
以上三个问题,从变量的个数及变量之间的关系看,它们有什么共同点?
关键词:两个变量,一个x值对应唯一确定的一个y值.
层数n 1 2 3 4 5 ······
物体总数y ······
想一想:
1
3
6
10
15
数学世家的光荣——函数的出现
17世纪,在瑞士的巴塞尔有一个祖孙五代数学家,成员数十人的家族——贝努利家族,其中最著名的是雅各、约翰、丹尼尔.欧拉从12岁起,就是这个家族成员的好朋友.他和同龄人尼古拉、丹尼尔结识,成为终生盟友,这两位兄长给欧拉讲了许多有趣的数学故事,吸引了他那颗幼小好奇的心灵,使欧拉从小立志,将来能像贝努利家族成员一样,腾飞于数学长空.1720年,欧拉在约翰·贝努利教授的推荐下,13岁成为巴塞尔大学的学生,从此他在约翰·贝努利的指导下迅速成长着.欧拉成为了贝努利家庭的一个成员,被世人传为佳话.
函数是中学数学中最重要的概念之一,函数
概念产生于300年前.笛卡儿引入了坐标系,使数
学发生了巨大变革,但他没用变量这个词.在数学
上使用变量这个词最早的是欧拉的老师约翰·贝努
利,他给函数下了这样的定义:“所谓变量的函数,
就是变量与常量组成的表达式”.
1775年,欧拉在《微分学》中给出了我们教科书中的定义.
读一读:
层数n 1 2 3 4 5 ······
物体总数y ······
速度v
距离s
高度h是时间t的函数
距离s是速度v的函数
1
3
6
10
15
物体总数y是层数n的函数
·
—数
——形
以上三个函数的表示方式有什么不同?
层数n 1 2 3 4 5 ······
物体总数y ······
想一想:
1
3
6
10
15
想一想:
不同点:在第一个问题中,是以图象的形式表示两个变量之间的关系,第二个问题中是列表的形式以表示两个变量之间的关系,第三个问题是以关系式的形式表示两个变量之间的关系.
函数常用的三种表示方式:
(1)图象法;(2)列表法;(3)关系式法.
以上三个函数的表示方式有什么不同?
以上三个问题中,自变量能取哪些值?
层数n 1 2 3 4 5 ······
物体总数y ······
想一想:
1
3
6
10
15
在龟兔赛跑问题中,如果将乌龟、兔子所走的路程分别记为s1和 s2,则 s1能看成是时间t的函数吗?为什么?s2能看成t的函数吗?
乌龟
兔子
( s1 )
( s2 )
问题解决:
·
·
·
思考生活中的某个变化过程,看看其中
是否存在函数关系,并指出自变量的取值范围.
具体要求:
四人为一小组,交流各自的想法;由一人负责整理大家的想法并向全班同学展示,其它同学可以补充.
联系生活:
1、下列各题中分别有几个变量?你能将其中某个变量看成另一个变量的函数吗?若能,请指出自变量的取值范围.
随堂练习:
2、已知菱形ABCD的对角线AC长为4,BD的长x在变化,则菱形的面积为y=-×4×x.本题中有几个变量?你能将其中某个变量看成另一个变量的函数吗?若能,请指出自变量的取值范围.
1
2
随堂练习:
3、在国内投寄60g以内的平信应付邮资如下表:
信件质量m/克
邮资y/元 1.20 2.40 3.60
上表中有几个变量?你能将其中某个变量看成另一个变量的函数吗?若能,请指出自变量的取值范围.
随堂练习:
通过这节课的学习,你有什么收获?
课堂小结:
1.知识内容:
2.学习流程:
3.思想与方法:
(1)函数的定义: 一般地,在某个变化过程中,有两个变量x和y,如果对于变量x的每一个值,变量y都有唯一的值与它对应,那么我们称y是x的函数,其中x是自变量,y是因变量.
(2)函数的三种表示方式:图象法;列表法;关系式法.
三个实际
问题讨论
总结共性
定义函数
问题解决
深入理解
联系生活
体会应用
数形结合思想;用函数的观点认识现实世界.
课后作业:
1.P77,知识技能1;
2.课下利用网络、书籍搜集关于函数的有关资料,在班内交流分享.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
