2023-2024学年黑龙江省哈尔滨市第三中学校高二下学期7月期末考试数学试题(含答案)
文档属性
| 名称 | 2023-2024学年黑龙江省哈尔滨市第三中学校高二下学期7月期末考试数学试题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 105.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-27 20:36:08 | ||
图片预览



文档简介
2023-2024学年黑龙江省哈尔滨市第三中学校高二下学期7月期末考试数学试题
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.命题“,”的否定是( )
A. , B. ,
C. , D. ,
2.已知,则“”是“”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
3.已知函数是幂函数,且在上单调递增,则( )
A. B. C. 或 D. 或
4.已知实数,,下列关系正确的是( )
A. B.
C. D.
5.函数在上单调递增,则的取值范围是( )
A. B. C. D.
6.函数有个极值点,则的取值范围是( )
A. B.
C. D.
7.已知甲盒中有个白球,个红球,个黑球,乙盒中有个白球,个红球,个黑球,现从甲盒中随机取出一个球放入乙盒,再从乙盒中随机取出一个球记事件“甲盒中取出的球与乙盒中取出的球颜色不同”,则( )
A. B. C. D.
8.已知函数,则不等式的解集为( )
A. B. C. D.
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.以下结论正确的是( )
A. 函数最小值为
B. 函数值域为
C. 函数值域为
D. 函数值域为
10.的展开式中各二项式系数和为,下列结论错误的( )
A. 展开式的所有项系数和为 B. 展开式中含项的系数为
C. 第项和第项的二项式系数相等 D. 展开式中常数项是第项
11.已知函数满足对任意,有,且,且当时,有,则下列说法中正确的是( )
A. B.
C. D.
三、填空题:本题共3小题,每小题5分,共15分。
12.函数的定义域是 .
13.初等数论中的四平方和定理最早由欧拉提出,后被拉格朗日等数学家证明四平方和定理的内容是:任意正整数都可以表示为四个自然数的平方和,例如正整数设,其中,,,均为自然数,则满足条件的有序数组的个数为 用数字作答
14.甲、乙二人进行羽毛球比赛,共比赛局,采用局胜制已知每局比赛中甲获胜的概率为,乙获胜的概率为,且每局比赛结果相互独立,记为比赛结束时的局数,则的期望的最大值为 .
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
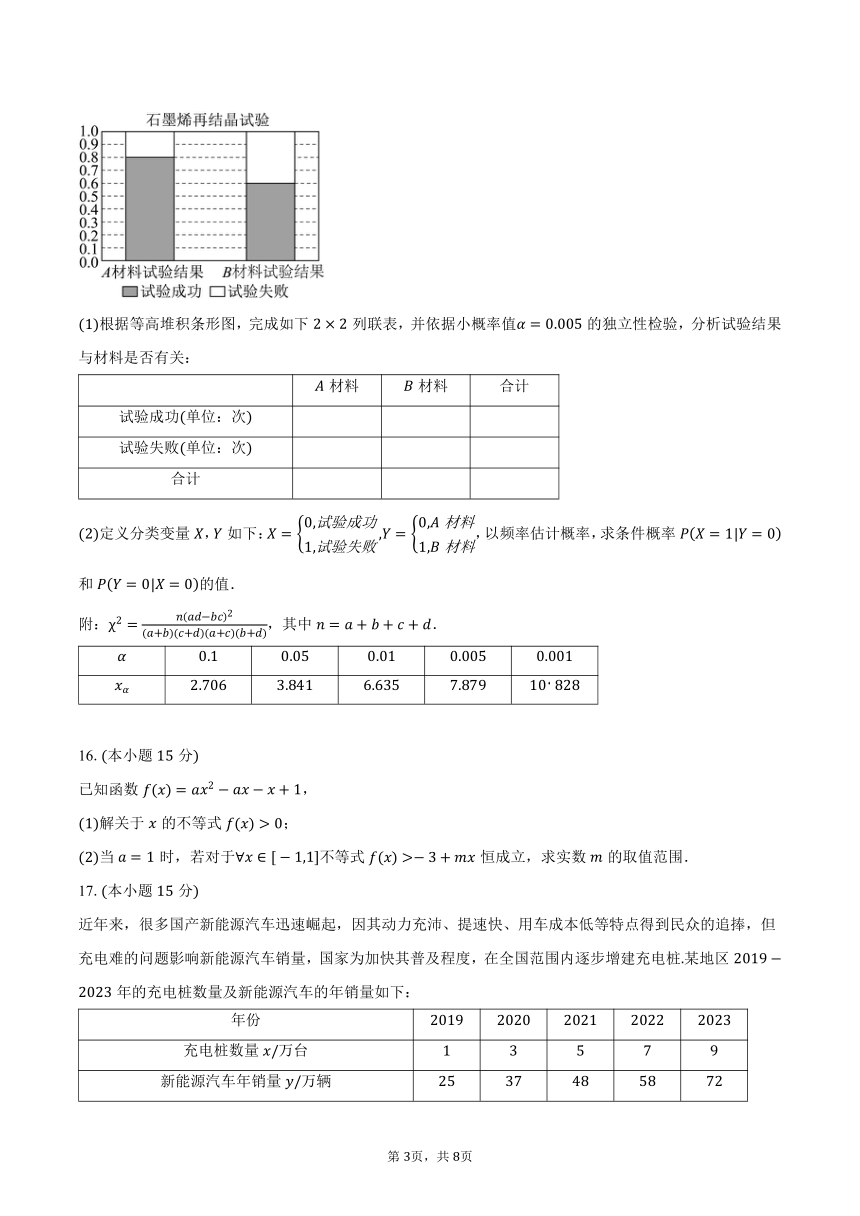
从石墨中通过化学气相沉积法分离出石墨烯,升华后附着在材料上再结晶制成石墨烯发热膜,广泛应用于冬装衣服现在有材料、材料可供选择,研究人员对附着在材料、材料上的石墨烯各做了次再结晶试验,得到如下等高堆积条形图.
根据等高堆积条形图,完成如下列联表,并依据小概率值的独立性检验,分析试验结果与材料是否有关:
材料 材料 合计
试验成功单位:次
试验失败单位:次
合计
定义分类变量,如下:,以频率估计概率,求条件概率和的值.
附:,其中.
16.本小题分
已知函数,
解关于的不等式;
当时,若对于不等式恒成立,求实数的取值范围.
17.本小题分
近年来,很多国产新能源汽车迅速崛起,因其动力充沛、提速快、用车成本低等特点得到民众的追捧,但充电难的问题影响新能源汽车销量,国家为加快其普及程度,在全国范围内逐步增建充电桩某地区年的充电桩数量及新能源汽车的年销量如下:
年份
充电桩数量万台
新能源汽车年销量万辆
已知可用线性回归模型拟合与的关系,请用样本相关系数加以说明与线性相关性的强弱结果精确到;已知,则认为线性相关性很强;,则认为线性相关性一般;,则认为线性相关性较弱
求关于的线性回归方程,预测当该地区充电桩数量为万台时,新能源汽车的年销量是多少万辆?
截止年年底,该地区新能源汽车充电桩个数占比情况为:类、类,现从该地区所有充电桩中,采用分层抽样的方式抽取个,再从抽取的个充电桩中不放回地随机抽取个,若表示抽到的类充电桩的数量,求的分布列和数学期望.
参考公式:相关系数,回归方程中斜率和截距的最小二乘估计公式分别为,.
参考数据:,,,.
18.本小题分
根据中华人民共和国国家标准,级防毒面具中综合过滤件的滤烟效率需要达到不低于的标准,某防护用品生产厂生产的综合过滤件的滤烟效率服从正态分布.
某质检员随机从生产线抽检件产品,测量出一只产品的滤烟效率为他立即要求停止生产,检查设备和工人工作状况请你依据所学知识,判断该质检员要求是否合理,并简要说明判断的依据;
该工厂将滤烟效率达到以上的综合过滤件定义为“优质品”.
求该生产线生产的一件综合过滤件为“优质品”的概率;
该企业生产了件这种综合过滤件,且每件产品相互独立,记为这件产品中“优质品”的件数,当为多少件时可能性最大即概率最大?
参考数据:,,.
19.本小题分
已知函数,.
若,求函数的单调区间;
若恒成立,求的取值范围;
若有两个零点,且,求证:.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.解:由堆积等高条形图得列联表:
材料 材料 合计
试验成功单位:次
试验失败单位:次
合计
零假设:试验结果与材料无关,
根据列联表中数据,得,
依据小概率值的独立性检验,推断假设不成立,
即试验结果与材料有关,此推断犯错误的概率不超过.
依题意,,
所以;
,
所以.
16.解:函数,不等式,
当时,解得;
当时,不等式化为,解得;
当时,不等式化为,若,则;
若,则或;若,则或,
所以当时,原不等式的解集为;当时,原不等式的解集为;
当时,原不等式的解集为;当时,原不等式的解集为.
当时,函数,不等式,
依题意,,不等式,当时,成立,,
当时,恒成立,而函数在上单调递减,
因此,则;
当时,恒成立,而函数在上单调递减,
因此,则,
所以实数的取值范围是.
17.解:依题意,,
而,,,
因此,
由与有相关系数近似为,得与的线性相关性很强,可以用线性回归模型拟合与的关系.
由知,,
,关于的线性回归方程为,
当时,,
所以当该地区充电桩数量为万台时,新能源汽车的年销量约为万辆.
依题意,抽取的个充电桩中,类充电桩有个,类充电桩有个,
的可能值为,
,,,
所以的分布列为:
数学期望.
18.解:由已知过滤件的 滤烟效率服从正态分布,,则,
由原则可知,生产的产品中滤烟效率在以外的值,发生的可能性很小,一旦发生,应停止生产.
令为“综合过滤件滤烟效率”,则一件过滤件为“优质品”的概率为
;
依题意得,记,
要使可能性最大,
则需
即,所以,即,
所以,
所以当为件时可能性最大.
19.解:当时,函数,求导得,
当时,,当时,,即在上递减,在上递增,
所以函数的递减区间是,递增区间是.
不等式,令,
求导得,当时,,当时,,
即函数在上递增,在上递减,因此,则,
所以的取值范围是.
由,得,由知,是直线与函数图象的两个交点的横坐标,
而,当时,恒成立,因此有两个零点时,,
由两边取对数得,于是
则,整理得,
令,由,得,即有,
则,解得,由,得
因此,令,求导得,
令,求导得,即在上单调递增,
当时,,即,函数在上单调递增,,
于是,所以.
第1页,共1页
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.命题“,”的否定是( )
A. , B. ,
C. , D. ,
2.已知,则“”是“”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
3.已知函数是幂函数,且在上单调递增,则( )
A. B. C. 或 D. 或
4.已知实数,,下列关系正确的是( )
A. B.
C. D.
5.函数在上单调递增,则的取值范围是( )
A. B. C. D.
6.函数有个极值点,则的取值范围是( )
A. B.
C. D.
7.已知甲盒中有个白球,个红球,个黑球,乙盒中有个白球,个红球,个黑球,现从甲盒中随机取出一个球放入乙盒,再从乙盒中随机取出一个球记事件“甲盒中取出的球与乙盒中取出的球颜色不同”,则( )
A. B. C. D.
8.已知函数,则不等式的解集为( )
A. B. C. D.
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.以下结论正确的是( )
A. 函数最小值为
B. 函数值域为
C. 函数值域为
D. 函数值域为
10.的展开式中各二项式系数和为,下列结论错误的( )
A. 展开式的所有项系数和为 B. 展开式中含项的系数为
C. 第项和第项的二项式系数相等 D. 展开式中常数项是第项
11.已知函数满足对任意,有,且,且当时,有,则下列说法中正确的是( )
A. B.
C. D.
三、填空题:本题共3小题,每小题5分,共15分。
12.函数的定义域是 .
13.初等数论中的四平方和定理最早由欧拉提出,后被拉格朗日等数学家证明四平方和定理的内容是:任意正整数都可以表示为四个自然数的平方和,例如正整数设,其中,,,均为自然数,则满足条件的有序数组的个数为 用数字作答
14.甲、乙二人进行羽毛球比赛,共比赛局,采用局胜制已知每局比赛中甲获胜的概率为,乙获胜的概率为,且每局比赛结果相互独立,记为比赛结束时的局数,则的期望的最大值为 .
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
从石墨中通过化学气相沉积法分离出石墨烯,升华后附着在材料上再结晶制成石墨烯发热膜,广泛应用于冬装衣服现在有材料、材料可供选择,研究人员对附着在材料、材料上的石墨烯各做了次再结晶试验,得到如下等高堆积条形图.
根据等高堆积条形图,完成如下列联表,并依据小概率值的独立性检验,分析试验结果与材料是否有关:
材料 材料 合计
试验成功单位:次
试验失败单位:次
合计
定义分类变量,如下:,以频率估计概率,求条件概率和的值.
附:,其中.
16.本小题分
已知函数,
解关于的不等式;
当时,若对于不等式恒成立,求实数的取值范围.
17.本小题分
近年来,很多国产新能源汽车迅速崛起,因其动力充沛、提速快、用车成本低等特点得到民众的追捧,但充电难的问题影响新能源汽车销量,国家为加快其普及程度,在全国范围内逐步增建充电桩某地区年的充电桩数量及新能源汽车的年销量如下:
年份
充电桩数量万台
新能源汽车年销量万辆
已知可用线性回归模型拟合与的关系,请用样本相关系数加以说明与线性相关性的强弱结果精确到;已知,则认为线性相关性很强;,则认为线性相关性一般;,则认为线性相关性较弱
求关于的线性回归方程,预测当该地区充电桩数量为万台时,新能源汽车的年销量是多少万辆?
截止年年底,该地区新能源汽车充电桩个数占比情况为:类、类,现从该地区所有充电桩中,采用分层抽样的方式抽取个,再从抽取的个充电桩中不放回地随机抽取个,若表示抽到的类充电桩的数量,求的分布列和数学期望.
参考公式:相关系数,回归方程中斜率和截距的最小二乘估计公式分别为,.
参考数据:,,,.
18.本小题分
根据中华人民共和国国家标准,级防毒面具中综合过滤件的滤烟效率需要达到不低于的标准,某防护用品生产厂生产的综合过滤件的滤烟效率服从正态分布.
某质检员随机从生产线抽检件产品,测量出一只产品的滤烟效率为他立即要求停止生产,检查设备和工人工作状况请你依据所学知识,判断该质检员要求是否合理,并简要说明判断的依据;
该工厂将滤烟效率达到以上的综合过滤件定义为“优质品”.
求该生产线生产的一件综合过滤件为“优质品”的概率;
该企业生产了件这种综合过滤件,且每件产品相互独立,记为这件产品中“优质品”的件数,当为多少件时可能性最大即概率最大?
参考数据:,,.
19.本小题分
已知函数,.
若,求函数的单调区间;
若恒成立,求的取值范围;
若有两个零点,且,求证:.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.解:由堆积等高条形图得列联表:
材料 材料 合计
试验成功单位:次
试验失败单位:次
合计
零假设:试验结果与材料无关,
根据列联表中数据,得,
依据小概率值的独立性检验,推断假设不成立,
即试验结果与材料有关,此推断犯错误的概率不超过.
依题意,,
所以;
,
所以.
16.解:函数,不等式,
当时,解得;
当时,不等式化为,解得;
当时,不等式化为,若,则;
若,则或;若,则或,
所以当时,原不等式的解集为;当时,原不等式的解集为;
当时,原不等式的解集为;当时,原不等式的解集为.
当时,函数,不等式,
依题意,,不等式,当时,成立,,
当时,恒成立,而函数在上单调递减,
因此,则;
当时,恒成立,而函数在上单调递减,
因此,则,
所以实数的取值范围是.
17.解:依题意,,
而,,,
因此,
由与有相关系数近似为,得与的线性相关性很强,可以用线性回归模型拟合与的关系.
由知,,
,关于的线性回归方程为,
当时,,
所以当该地区充电桩数量为万台时,新能源汽车的年销量约为万辆.
依题意,抽取的个充电桩中,类充电桩有个,类充电桩有个,
的可能值为,
,,,
所以的分布列为:
数学期望.
18.解:由已知过滤件的 滤烟效率服从正态分布,,则,
由原则可知,生产的产品中滤烟效率在以外的值,发生的可能性很小,一旦发生,应停止生产.
令为“综合过滤件滤烟效率”,则一件过滤件为“优质品”的概率为
;
依题意得,记,
要使可能性最大,
则需
即,所以,即,
所以,
所以当为件时可能性最大.
19.解:当时,函数,求导得,
当时,,当时,,即在上递减,在上递增,
所以函数的递减区间是,递增区间是.
不等式,令,
求导得,当时,,当时,,
即函数在上递增,在上递减,因此,则,
所以的取值范围是.
由,得,由知,是直线与函数图象的两个交点的横坐标,
而,当时,恒成立,因此有两个零点时,,
由两边取对数得,于是
则,整理得,
令,由,得,即有,
则,解得,由,得
因此,令,求导得,
令,求导得,即在上单调递增,
当时,,即,函数在上单调递增,,
于是,所以.
第1页,共1页
同课章节目录
